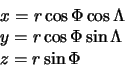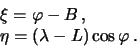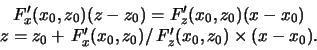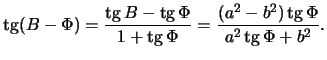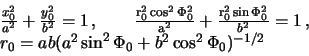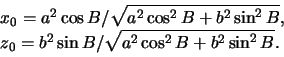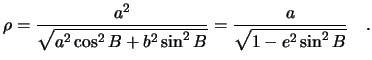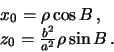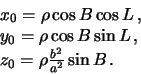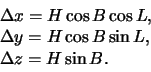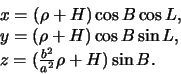---

<< Лекция 1. Теория фигуры земли | Оглавление | Лекция 3. Теория потенциала >>

Разделы

• 2.1 Декартовы системы координат
• 2.2 Сферическая система координат
• 2.3 Геодезическая система координат
• 2.4 Эллипсоидальная система координат

---

Лекция 2. Геодезические системы координат

Сферическая система. Широта долгота и радиус-вектор. Система координат, построенная на эллипсоиде. Геодезические координаты: широта, долгота и высота. Связь между сферической, геодезической и декартовой системами координат.

Геодезические задачи решают на плоскости, если размеры площади невелики. Если исследуемая часть поверхности занимает несколько градусов широты или долготы, то необходимо учитывать и кривизну поверхности. В этом случае часто подходит и шар. Для решения глобальных задач, в том числе и задач по космической геодезии в качестве тела отсчета берут эллипсоид вращения. В частности на эллипсоиде решают следующие задачи:

--

Уточнение формы и размеров общего земного эллипсоида (ОЗЭ).

--

Перенос направлений и расстояний с физической поверхности на эллипсоид.

--

Определение координат точек на поверхности референц-эллипсоида.

--

Определение расстояний между точками с заданными координатами.

--

Уточнение координат по мере уточнения элементов эллипсоида.

2.1 Декартовы системы координат

Введем две прямоугольные системы координат: локальную и глобальную.

Начало системы отсчета (точка Р) для локальной прямоугольной системы координат выберем в точке наблюдения, лежащей на поверхности эллипсоида. Ось РХ направим на Север, ось РУ? на Восток, а ось по нормали к поверхности эллипсоида вниз (по внутренней нормали). В этой системе координат "горизонтальная" плоскость ХРУ не совпадает с плоскостью астрономического горизонта.

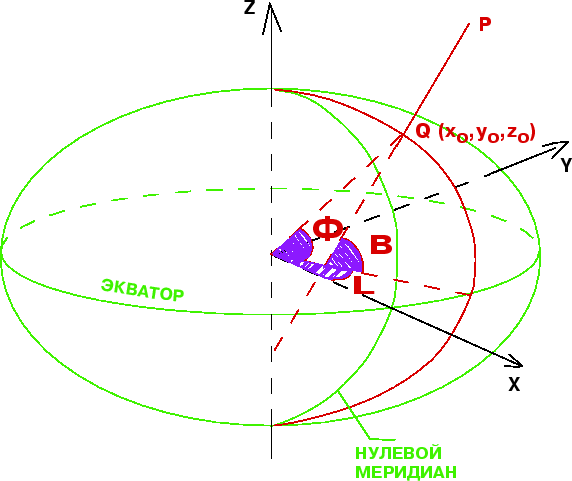
Глобальную декартову геодезическую систему координат Oxyz строят так:
начало отсчета совмещают с центром ОЗЭ (не путать с центром масс Земли!), плоскость xOy -- c плоскостью экватора. Ось Ox совмещают с линией пересечения плоскости нулевого меридиана и плоскости экватора. Ось Oy пересекает экватор в точке с долготой 90°. Ось Oz совпадает с осью вращения ОЗЭ. Эта ось не обязательно совпадает с осью вращения Земли. Для трехосного ОЗЭ начало координат берут в центре масс Земли, а оси -- совпадающими с главными осями инерции. В этом случае плоскость xOy, вообще говоря, не будет лежать в плоскости экватора.

2.2 Сферическая система координат

Телом отсчета для сферической системы координат является сфера с радиусом . Начало этой системы координат совмещают с центром сферы. Координатами являются геоцентрическая широта , долгота и радиус-вектор . Широтой называется угол между радиусом-вектором и плоскостью экватора. Долгота есть угол между плоскостью, проходящей через заданную точку и осью вращения (плоскость меридиана) и плоскостью меридиана, принятого в качестве нулевого. Связь между сферической системой и глобальной декартовой определяется формулами

В том случае, когда широта определяется как угол между плоскостью экватора и отвесной линией, сферическая система координат называется астрономической. Широта и долгота, определенные в этой системе мы будем обозначать через и .

2.3 Геодезическая система координат

С геодезической системой координат связывают понятия геодезической широты, долготы и высоты. Геодезическая широта В есть угол, под которым пересекается нормаль к поверхности эллипсоида с плоскостью экватора. Долгота -- двугранный угол между плоскостью нулевого меридиана и плоскостью меридиана, проходящего через заданную точку.

Геодезические широта и долгота отличаются от соответствующих астрономических координат, связанных с отвесной линией, так как отвесная линия не совпадает с нормалью к эллипсоиду. Отклонение отвесной линии можно спроецировать на две плоскости: плоскость меридиана и плоскость первого вертикала. Нетрудно понять, что обе эти составляющие можно определить через разности между астрономическими и геодезическими координатами

Отклонения отвесной линии составляют, как правило, первые несколько секунд дуги.

Заметим, что геодезическая и геоцентрическая долготы совпадают. Обе они определены как двугранный угол между плоскостью нулевого меридиана и плоскостью, содержащей ось вращения и заданную точку. Геоцентрическая же широта отличается от геодезической.

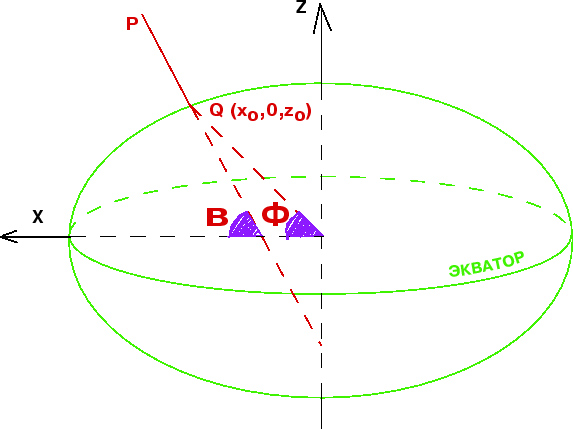
Рассмотрим точку , лежащую вне ОЗЭ. Опустим из этой точки перпендикуляр на поверхность эллипсоида и продолжим его до пересечения с экваториальной плоскостью (рис. 2). Проекцию точки на поверхность эллипсоида обозначим через Тогда отрезок PQ есть геодезическая высота точки . Угол, под которым упомянутый перпендикуляр пересекает плоскость экватора, есть геодезическая широта . Она относится как к точке , так и к точке . Геоцентрические широты этих двух точек, как видно из рисунка, различаются. Геоцентрическая широта точки угол между радиус-вектором этой точки и плоскостью экватора.

Установим связь между координатами точки , сжатием эллипсоида и широтами и . Поскольку точка лежит на поверхности эллипсоида, то ее прямоугольные координаты подчиняются уравнению эллипсоида вращения: . Рассмотрим сечение . Тогда, как легко видеть, . Чтобы определить , нужно найти угловой коэффициент нормали в точке . Уравнение нормали к кривой в точке имеет вид

У нас , поэтому , ,

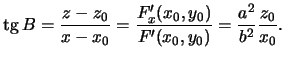
Следовательно,

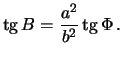
Определим отличие геоцентрической широты от геодезической . Имеем очевидные равенства

Второй эксцентриситет эллипса, как мы знаем, определяется следующим образом , поэтому

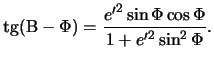
Для Земли второй эксцентриситет мал, поэтому, пренебрегая малыми второго порядка относительно сжатия, получим . Можно также считать, что

Учитывая сказанное, получим

Наибольшее отличие геодезической широты от геоцентрической достигается на широте 45° и составляет .

Связь глобальных декартовых координат с геоцентрическими определяется формулами (2.1). Определим теперь формулы, связывающие декартовы координаты с геодезическими. Это означает, что бы должны определить координаты точки через параметры эллипсоида и геодезические широту и долготу.

Поскольку , для определения координат , , точки достаточно, для начала, определить только координаты и , то есть все рассуждения проводить только для сечения . Обратимся к рис. 3.

Определим прямоугольные координаты точки , расположенной на высоте Н над поверхностью эллипсоида. Сначала определим координаты проекции точки на поверхность эллипсоида (точка ). Ее координаты в сечении Охz равны

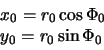
Индексом "0" мы отметили принадлежность координат к точке, лежащей на поверхности эллипсоида. Как мы видели

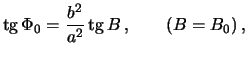
поэтому

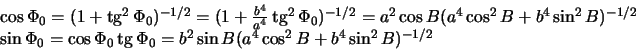
Остается определить радиус-вектор точки . Воспользуемся уравнением эллипса и выполним необходимые преобразования.

Выразим и через и , для чего воспользуемся приведенными выше формулами. Определим радиус-вектор точки

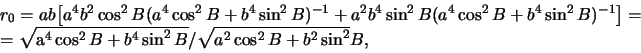
следовательно,

Обозначим

Теперь

Для произвольного сечения, проходящего через ось вращения , будем иметь

Теперь поднимем точку на высоту Н и совместим ее с точкой . Прямоугольные координаты изменятся на

Окончательно, теперь формулы для пересчета геодезических координат и Н в прямоугольные примут вид

Здесь , определенный формулой (2.7) имеет простой геометрический смысл: он равен отрезку нормали, проходящей через точку , от этой точки до точки пересечения ее с осью вращения эллипсоида. Справедливость этого утверждения предлагается доказать самостоятельно.

2.4 Эллипсоидальная система координат

Рассмотрим еще одну систему координат, имеющую приложение в теории гравитационного потенциала:

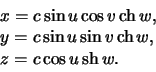
Эти формулы содержат не три, а четыре переменные величины. Четвертая переменная устанавливает семейство координатных поверхностей -- эллипсоидов. Убедимся в этом. Проделаем простые преобразования:

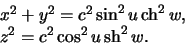
Разделив первое уравнение на а второе -- на , получим

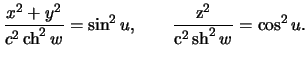
Очевидно, что при получим уравнение эллипсоида вращения

где

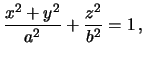
Поскольку , имеем , отсюда параметр имеет простой физический смысл: он равен половине межфокусного расстояния. Понятно, что изменяя при условии , получим семейство софокусных эллипсоидов, играющих важную роль в теории потенциала фигур равновесия Построим теперь семейство координатных поверхностей . Проделаем очевидные преобразования

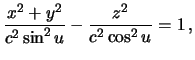
меняя , получим семейство однополостных гиперболоидов вращения. Обозначив , , получим уравнение гиперболоида в общепринятой форме.

Разделив у на х, получим . Изменяя , получим семейство плоскостей, проходящее через ось Оz. Все три семейства поверхностей образуют взаимно ортогональную систему.

---

<< Лекция 1. Теория фигуры земли | Оглавление | Лекция 3. Теория потенциала >>

Публикации с ключевыми словами: гравиметрия - потенциал - гравитационное поле - фигура Земли - геодезия Публикации со словами: гравиметрия - потенциал - гравитационное поле - фигура Земли - геодезия
См. также: Сагитовские чтения - 2007 Венера: пролетая мимо Сагитовские чтения - 2006 К 90-летию Николая Пантелеймоновича Грушинского Сагитовские чтения - 2005 Простейшая форма представления градиента гравитационного потенциала небесных тел Гора Олимп с орбиты Все публикации на ту же тему >>