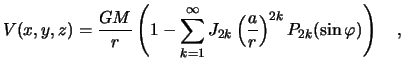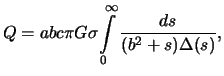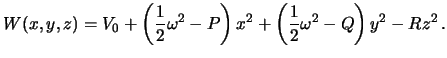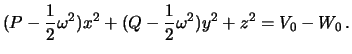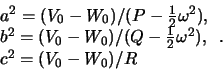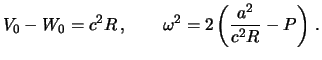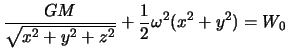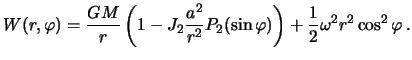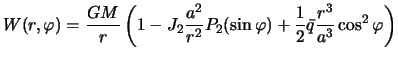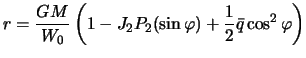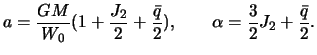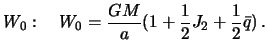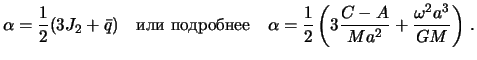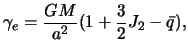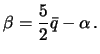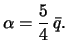<< 4.1 Потенциал тяжести | Оглавление | 4.3 Гравитационные аномалии и ... >>
- 4.2.1 Основные теоремы
- 4.2.2 Эллипсоид как фигура равновесия
- 4.2.3 Модель "планеты Роша"
- 4.2.4 Сфероид Клеро
- 4.2.5 Два предела сжатия для фигур равновесия
4.2 Фигуры равновесия небесных тел
Все планеты Солнечной системы находятся в состоянии, близком к
гидростатическому равновесию.
Мы уже говорили, что планеты с массой больше ![]() т имеют шарообразную
форму, потому что массы, слагающие тело планет, обладают свойством
пластичности. Планеты приобретают форму, как если бы они были жидкими. В
этом случае уровенная поверхность будет поверхностью планеты. В
действительности поверхность планеты не совпадает с уровенной поверхностью.
Эти отличия свидетельствуют об отклонениях от состояния гидростатического
равновесия и являются предметом изучения геофизиков и геодезистов. Введены
специальные термины тля обозначения поверхностей уровня для планет.
Эквипотенциальная поверхность Земли, по предложению Листинга, называется
геоидом. По аналогии, уровенную поверхность для Луны называют селеноидом, уровенную поверхность
Марса -- ареоидом, и т.п
т имеют шарообразную
форму, потому что массы, слагающие тело планет, обладают свойством
пластичности. Планеты приобретают форму, как если бы они были жидкими. В
этом случае уровенная поверхность будет поверхностью планеты. В
действительности поверхность планеты не совпадает с уровенной поверхностью.
Эти отличия свидетельствуют об отклонениях от состояния гидростатического
равновесия и являются предметом изучения геофизиков и геодезистов. Введены
специальные термины тля обозначения поверхностей уровня для планет.
Эквипотенциальная поверхность Земли, по предложению Листинга, называется
геоидом. По аналогии, уровенную поверхность для Луны называют селеноидом, уровенную поверхность
Марса -- ареоидом, и т.п
4.2.1 Основные теоремы
Теорема Ляпунова
Единственно устойчивой фигурой равновесия покоящейся жидкости является сфера.
Следствием этой теоремы можно усмотреть шарообразность всех планет Солнечной системы.
Теорема Пуанкаре
Единственно возможным движением жидкости, находящейся в состоянии относительного равновесия, является равномерное вращение вокруг одной из главных осей инерции. Понятно, что в случае, когда планета близка к состоянию гидростатического равновесия, ее ось вращения почти совпадает с главной осью инерции.
Теорема Лихтенштейна
Фигура равновесия однородной жидкости всегда симметрична относительно плоскости, проходящей через центр инерции и перпендикулярной к оси вращения.
Эту теорему называют еще теоремой о существовании экватора.
Исследования показали, что потенциал притяжения гидростатически равновесной планеты содержит лишь четные зональные гармоники :
причем мультипольные моменты ![]() убывают как
убывают как ![]()
4.2.2 Эллипсоид как фигура равновесия
Как мы уже говорили, внутри однородного эллипсоида, как и для шара, сила
притяжения подчиняется закону Гука: она прямо пропорциональна отклонению
материальной точки от положения равновесия. В теории потенциала доказано,
что силовая функция для внутренней точки имеет вид
![]() .
Тогда компоненты силы притяжения пропорциональны
координатам притягиваемой точки
.
Тогда компоненты силы притяжения пропорциональны
координатам притягиваемой точки
![]() . Здесь
. Здесь
![]() ,
, ![]() ,
, ![]() и
и ![]() -- постоянные, зависящие от плотности и параметров эллипсоида и
не зависящие от координат точки. Приведем эти формулы без вывода
-- постоянные, зависящие от плотности и параметров эллипсоида и
не зависящие от координат точки. Приведем эти формулы без вывода
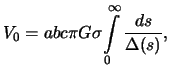
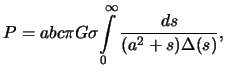
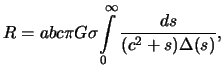
где
Если притягиваемая материальная точка -- внешняя, то для нее силовая функция
сохраняет тот же вид, но
![]() перестают быть постоянными, а
зависят от координат точки. Для их вычисления справедливы те же интегралы,
что и для внутренней точки, но нижний предел не нуль, а величина
перестают быть постоянными, а
зависят от координат точки. Для их вычисления справедливы те же интегралы,
что и для внутренней точки, но нижний предел не нуль, а величина ![]() ,
которая выбирается таким образом, чтобы эллипсоид
,
которая выбирается таким образом, чтобы эллипсоид
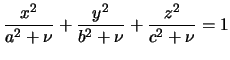
проходил через заданную внешнюю точку.
Потенциал тяжести от потенциала притяжения отличается тем, что аддитивно содержит потенциал
центробежной силы
![]() . Подставляя сюда выражение для потенциала притяжения
эллипсоида, получим
. Подставляя сюда выражение для потенциала притяжения
эллипсоида, получим
Если поверхность эллипсоида является поверхностью уровня, то такой эллипсоид
будет гидростатически равновесным. Уравнением уровенной поверхности будет
![]() , где
, где ![]() -- постоянная величина. Возникает вопрос,
можно ли подобрать такую угловую скорость вращения для трехосного эллипсоида
с заданными полуосями, чтобы его поверхность оказалась поверхностью уровня? Нетрудно
убедиться, что нельзя.
-- постоянная величина. Возникает вопрос,
можно ли подобрать такую угловую скорость вращения для трехосного эллипсоида
с заданными полуосями, чтобы его поверхность оказалась поверхностью уровня? Нетрудно
убедиться, что нельзя.
Уравнением трехосного эллипсоида в данном случае будет выражение
Определим большие полуоси
Очевидно, что если из первого уравнения мы определим угловую скорость, то совсем не обязательно, чтобы эта угловая скорость удовлетворяла второму уравнению. Тем не менее специалистами в области теории фигур равновесия небесных тел доказано существование равновесных трехосных эллипсоидов, которые получили название эллипсоидов Якоби.
4.2.2.1 Эллипсоид Маклорена
В частном случае ![]() , поэтому
, поэтому ![]() . Из уравнение (4.6) получим
. Из уравнение (4.6) получим
Полученные уравнения определяют и постоянную
![]() и
и ![]() . По-видимому, для любых заданных полуосях
эллипсоида вращения можно найти угловую скорость вращения, такую, что данный
эллипсоид становится фигурой равновесия.
. По-видимому, для любых заданных полуосях
эллипсоида вращения можно найти угловую скорость вращения, такую, что данный
эллипсоид становится фигурой равновесия.
4.2.3 Модель "планеты Роша"
Под "планетой Роша" мы будем понимать такую фигуру равновесия, в которой вся притягивающая масса сосредоточена в и одной точке -- центре масс, а вектор силы тяжести образуют векторная сумма силы притяжения и центробежной силы. Тогда уравнением "поверхности" такой планеты будет
Рассмотрим, сначала, как выглядит поверхность уровня вблизи начала
координат. В этом случае величину
![]() можно
считать малой, а
можно
считать малой, а ![]() , наоборот, большой. Пренебрегая в (4.8) вторым
слагаемым в левой части формулы, получим
, наоборот, большой. Пренебрегая в (4.8) вторым
слагаемым в левой части формулы, получим
![]() . Это
уравнение замкнутой поверхности, которая по мере приближения к началу
координат становится все более похожей на сферу. Назовем ее псевдосферой.
. Это
уравнение замкнутой поверхности, которая по мере приближения к началу
координат становится все более похожей на сферу. Назовем ее псевдосферой.
По мере отдаления от начала координат в плоскости ![]() мы достигнем таких
точек, в которых сила притяжения и центробежная сила становятся равными и
противоположно направленными, то есть
мы достигнем таких
точек, в которых сила притяжения и центробежная сила становятся равными и
противоположно направленными, то есть
![]() ,
Отсюда
,
Отсюда
![]() . Мы получили уравнение окружности с
радиусом, равным
. Мы получили уравнение окружности с
радиусом, равным
![]() Понятно, что во всех
точках этой окружности силы тяжести равна нулю.
Понятно, что во всех
точках этой окружности силы тяжести равна нулю.
Если двигаться дальше от начала координат, мы придем к варианту, когда
![]() будет большой величиной, а
будет большой величиной, а ![]() , наоборот, малой. Тогда
пренебрегая первым членом в формуле (4.8), получим уравнение поверхности,
близкой к круговому цилиндру
, наоборот, малой. Тогда
пренебрегая первым членом в формуле (4.8), получим уравнение поверхности,
близкой к круговому цилиндру
![]() .
Это уже разомкнутая поверхность уровня. Планеты с такой поверхностью
существовать не может.
.
Это уже разомкнутая поверхность уровня. Планеты с такой поверхностью
существовать не может.
Таким образом, гидростатически равновесная планета может существовать только внутри "полости Роша", где сила тяжести всюду отлична от нуля и направлена по нормали внутрь этой поверхности. Поверхность такой планеты имеет овальную форму, сплюснутую с полюсов.
4.2.4 Сфероид Клеро
Сфероидом в геодезии называют поверхность вращения, близкую к сфере. В первом приближении в качестве уравнения сфероида можно принять
Очевидно, что на экваторе ![]() , а на полюсах
, а на полюсах
![]() ,
,
![]() . Фигура, уравнение
которой удовлетворяет формуле (4.9) обладает сжатием: полярный радиус ее меньше
экваториального. Из определения следует, что
. Фигура, уравнение
которой удовлетворяет формуле (4.9) обладает сжатием: полярный радиус ее меньше
экваториального. Из определения следует, что
![]() .
.
Установим связь между коэффициентом ![]() и сжатием планеты. Из формулы
(3.18) следует, что потенциал притяжения равен
и сжатием планеты. Из формулы
(3.18) следует, что потенциал притяжения равен
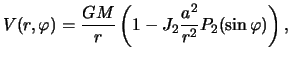
а потенциал тяжести --
В приведенной формуле мы ограничились лишь коэффициентом ![]() , отбросив
все остальные мультипольные моменты, так как в случае гидростатически
равновесной фигуры, они будут иметь более высокий порядок малости, чем
постоянная
, отбросив
все остальные мультипольные моменты, так как в случае гидростатически
равновесной фигуры, они будут иметь более высокий порядок малости, чем
постоянная ![]() .
.
Введем обозначение
![]() . Новая малая величина есть, грубо говоря,
отношение центробежной силы на экваторе к силе притяжения. Следовательно
. Новая малая величина есть, грубо говоря,
отношение центробежной силы на экваторе к силе притяжения. Следовательно
![]() . Подставим полученное
выражение в (4.10) и вынесем за общие скобки отношение
. Подставим полученное
выражение в (4.10) и вынесем за общие скобки отношение ![]() :
:
Приравнивая полученное выражение постоянной ![]() , получим уравнение
сфероида.
, получим уравнение
сфероида.
Теорема Клеро устанавливает связь между параметрами сфероида, силой тяжести на его поверхности и коэффициентами разложения гравитационного потенциала.
Сжатие сфероида Клеро.
Сравним формулу (4.11) с (4.9).
Учитывая, что
![]() -- малые
величины, запишем приближенное равенство
-- малые
величины, запишем приближенное равенство
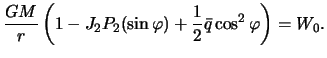
Решим полученное выражение относительно ![]()
Чтобы отождествить полученную формулу с уравнением сфероида (4.9), примем во внимание, что
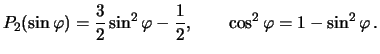
Поставляя эти равенства в (4.12), получим
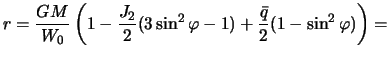
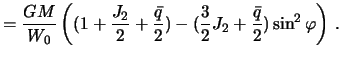
Сравнивая полученное выражение с (4.9) и учитывая, что
![]() и
и ![]() -- малые величины, получим
-- малые величины, получим
Отсюда определяем постоянную
Итак, первая часть теоремы Клеро устанавливается связь между сжатием равновесной планеты с первым коэффициентом зональной гармоники разложения гравитационного потенциала и угловой скоростью вращения планеты.
Вторая часть теоремы Клеро определяет зависимость силы тяжести на поверхности равновесной планеты от широты.
Сила тяжести на поверхности сфероида Клеро.
Вернемся снова к формуле потенциала тяжести для сфероида (4.11). Для того, чтобы получить силу тяжести нам нужно потенциал продифференцировать по нормали к поверхности уровня. Однако, поскольку наш сфероид мало отличается от сферы, дифференцирование по нормали мы заменим дифференцированием по радиус-вектору, что значительно проще.
Обозначив производную по радиус-вектору буквой ![]() , получим
, получим
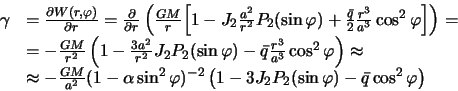
С точностью до малых величин первого порядка будем иметь
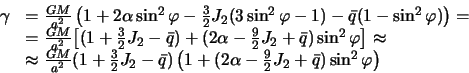
Сила тяжести на экваторе, согласно полученной формуле, равна
а для любой широты
где
![]() .
С помощью (4.15)
исключим
.
С помощью (4.15)
исключим ![]() :
:
![]() , то есть
, то есть
здесь
![]() .
.
Формулами (4.17) и (4.18) мы и завершим изложение теоремы Клеро.
4.2.5 Два предела сжатия для фигур равновесия
Коснемся сначала истории нашего вопроса. И.Ньютон (1643-1727) для объяснения
явления, которое заметили многое астрономы, отъезжающие в экспедиции для
наблюдений солнечного затмения в экваториальную зону, астрономические часы
маятникового типа отстают по сравнению с Парижской обсерваторией, где они
строго выверялись, на 2,5 минуты в сутки. Ньютон предположил, что виной тому
служит эллипсоидальная форма Земли и, естественно, ее суточное вращение.
Предполагая, что Земля -- однородный эллипсоид вращения, он получил, что
сжатие земного эллипсоида должно быть равным 1,25 ![]() =1:230.
=1:230.
Современник Ньютона Гюйгенс (1629-1695) решает ту же задачу, но другим
путем. Он предположил, что силы притяжения направлены к центру, а эллипсоидальность
поверхности уровня возникает только за счет центробежной силы. Таким
образом, если Ньютон в качестве фигуры равновесия брал эллипсоид Маклорена,
то Гюйгенс -- фигуру, которую мы назвали "планетой Роша". Он получил, что
сжатие равно 0.5 ![]() = 1:576. Результат, который значительно отличается
Ньютоновской оценки сжатия.
= 1:576. Результат, который значительно отличается
Ньютоновской оценки сжатия.
Вернемся к теории Клеро. Согласно его теории сжатие равновесной планеты
должно быть равно
![]() . Первый предел сжатия получим, если примем Земли однородным
двухосным эллипсоидом, для которого
. Первый предел сжатия получим, если примем Земли однородным
двухосным эллипсоидом, для которого
![]() ,
,
![]() . Отсюда
. Отсюда
![]() .
.
Но
![]() ,
,
![]() ,
,
![]() .
Следовательно
.
Следовательно
![]() и, наконец,
и, наконец,
Мы получили то же значение, что и Ньютон, правда с точностью до первой степени сжатия.
Второй предел сжатия, мы получим, если будем считать все притягивающие массы
шаром, тогда ![]() и
и
Таким образом. реальное сжатие лежит между этими двумя пределами
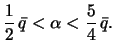
Для иллюстрации сказанного приведем сжатия некоторых планет Солнечной системы, а также их возможные предельные значения
Сравнивая значения сжатия, мы видим, что фигура планеты в значительно степени зависит от ее внутреннего строения. Планеты Земля и Марс весьма далеки от того строения, которое принял Гюйгенс: планета имеет компактное твердое притягивающее тело, окруженное рыхлой оболочкой. По величине сжатия можно судить о том, что к такой модели более подходят планеты гиганты.
Приведенные данные взяты из книги акад. А.А. Михайлова "Курс гравиметрии и теории фигуры Земли", опубликованной в 1939 году. Современные данные могут несколько отличаться от приведенных, хотя общая картина не изменится.
<< 4.1 Потенциал тяжести | Оглавление | 4.3 Гравитационные аномалии и ... >>
|
Публикации с ключевыми словами:
гравиметрия - геофизика - солнечная система - сейсмология
Публикации со словами: гравиметрия - геофизика - солнечная система - сейсмология | |
См. также:
Все публикации на ту же тему >> | |