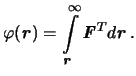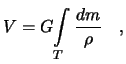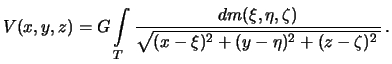<< 2.6 Землетрясения | Оглавление | 3.2 Свойства потенциала >>
3. Гравитационное поле планеты
Разделы
- 3.1 Гравитационный потенциал
- 3.2 Свойства гравитационного потенциала
- 3.3 Гравитационный потенциал шара
- 3.4 Гравитационное поле планеты
3.1 Гравитационный потенциал
Подразделы
Потенциалом называется работа, которую нужно совершить, которую нужно
совершить, чтобы переместить данную материальную точку с массой, равной
единице, из заданной точки в бесконечность. Пусть
![]() есть
вектор-сила, приложенная к материальной точке,
есть
вектор-сила, приложенная к материальной точке,
![]() -- радиус-вектор
этой точки. Тогда потенциалом будет величина
-- радиус-вектор
этой точки. Тогда потенциалом будет величина
Введем понятие силовой функции ![]() . По определению частная производная
силовой функции вдоль любого направления
. По определению частная производная
силовой функции вдоль любого направления ![]() равна компоненте силы вдоль этого
направления. Отсюда следует, что
равна компоненте силы вдоль этого
направления. Отсюда следует, что
![]() .
.
Таким образом, подынтегральное выражение в формуле (3.1) есть не что иное, как полный дифференциал силовой функции, поэтому
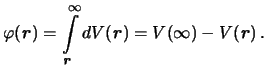
Силовую функцию на бесконечности можно приравнять нулю, поэтому будем считать, что потенциал и силовая функция отличаются лишь знаком.
В гравиметрии, как разделе геофизики, традиционно не разделяют эти два понятия, и под термином гравитационный потенциал обычно понимают силовую функцию. В нашем курсе мы также будем придерживаться этих традиций.
3.1.1 Гравитационный потенциал материальной точки
Согласно закону Ньютона, две материальные точки притягиваются друг к другу с
силой, прямо пропорциональной их массам и обратно пропорционально квадрату
расстояния между ними. Выберем систему координат так, чтобы одна из
материальных точек оказалась в начале этой системы. Тогда другая
материальная точка будет иметь радиус-вектор
![]() . Вектор
напряженности гравитационного поля в точке с радиус-вектором
. Вектор
напряженности гравитационного поля в точке с радиус-вектором
![]() равен силе, которая действует на материальную точку с массой, равной
единице. Вектор этой силы можно изобразить следующим образом
равен силе, которая действует на материальную точку с массой, равной
единице. Вектор этой силы можно изобразить следующим образом
![]() , где
, где ![]() -- гравитационная постоянная. Проекции
этой силы на оси декартовой системы координат будут равны
-- гравитационная постоянная. Проекции
этой силы на оси декартовой системы координат будут равны
![]() ,
,
![]() ,
,
![]() . Абсолютная величина этого
вектора, равна
. Абсолютная величина этого
вектора, равна
Заметим, что размерность напряженности поля тяготения совпадает с размерностью ускорения, поэтому часто вместо силы притяжения единицы массы, или удельной силы притяжения говорят об ускорении силы притяжения, хотя, может быть, в этом словосочетании можно усмотреть и смысловую нелепицу.
Формулу (3.2) еще называют как закон обратных квадратов. Весь опыт небесной механики говорит о том, что в масштабах Солнечной системы он работает очень хорошо: не найдено каких либо подозрений, что его нужно подправлять. Лабораторные эксперименты по определению гравитационной постоянной G дали повод подозревать, что этот закон не абсолютно строг. Хотя причиной несоответствия теории и практики вполне могли быть и неизвестные систематические погрешности. В конце минувшего века наблюдался повышенный интерес к закону обратных квадратов. В разных странах проводились эксперименты и применялись современные самые высокоточные инструменты для обнаружения каких-либо невязок между теорией и практикой. Однако, никаких значимых расхождений не обнаружено.
Нетрудно убедиться, что гравитационный потенциал точки (силовая функция)
равен,
![]() , где
, где ![]() -- расстояние между притягивающимися
точками (скалярная величина).
-- расстояние между притягивающимися
точками (скалярная величина).
3.1.2 Гравитационный потенциал тела
Строго говоря, закон обратных квадратов работает только для материальных точек. Однако, физики-теоретики и экспериментаторы доказывают, что для гравитационного поля выполняется принцип суперпозиции: гравитационное поле двух материальных точек (или тел) равно сумме гравитационных полей каждой из этих точек (или тел) по отдельности. Иначе говоря, силы тяготения не экранируются.
Согласно принципа суперпозиции, гравитационный потенциал ![]() точек равен сумме
гравитационных потенциалов всех точек
точек равен сумме
гравитационных потенциалов всех точек
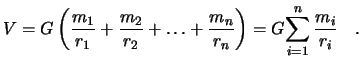
Если точек бесконечное число, а массы их бесконечно малы, то имеем дело с интегральной суммой, и нашу формулу следует записать так
где ![]() -- расстояние между фиксированной точкой
-- расстояние между фиксированной точкой ![]() и элементом притягивающей массы
и элементом притягивающей массы
![]() .
.
Пусть ![]() ,
, ![]() ,
, ![]() -- координаты точки
-- координаты точки ![]() , а
, а ![]() ,
, ![]() ,
, ![]() -- координаты текущей точки с массой dm тогда
формулу (3.3) можно переписать следующим образом м
-- координаты текущей точки с массой dm тогда
формулу (3.3) можно переписать следующим образом м
Приведенный интеграл берется по всему объему тела, это трехкратный интеграл.
Его величина зависит от распределения плотностей внутри тела.
<< 2.6 Землетрясения | Оглавление | 3.2 Свойства потенциала >>
|
Публикации с ключевыми словами:
гравиметрия - геофизика - солнечная система - сейсмология
Публикации со словами: гравиметрия - геофизика - солнечная система - сейсмология | |
См. также:
Все публикации на ту же тему >> | |