<< 9.1 Полезные формулы | Оглавление | 9.3 Результаты изучения ... >>
9.2 Проблемы исследования далеких галактик
К сожалению, существуют по крайней мере три
принципиальных фактора, сильно затрудняющих наблюдательное
исследование далеких галактик. Первые два связаны с расширением
Вселенной, а третий -- с эволюцией их характеристик со временем.
![]() Ослабление яркости
Ослабление яркости
Первая из помех -- это так называемое
космологическое ослабление поверхностной яркости, зависящее в модели
расширяющейся Вселенной только от красного смещения:
Как видно из (98), расширение Вселенной приводит к
обескураживающе быстрому падению поверхностной яркости с ростом ![]() .
Объекты с
.
Объекты с ![]() имеют в 3
имеют в 3![]() раз меньшие яркости
(или, в звездных величинах,
раз меньшие яркости
(или, в звездных величинах, ![]() ) по сравнению с
аналогичными объектами вблизи нас. Галактики с
) по сравнению с
аналогичными объектами вблизи нас. Галактики с ![]() ослабевают
на 7 звездных величин (!). Следовательно, даже с помощью космических
наблюдений среди далеких галактик нам доступны лишь те, которые имеют
очень высокую поверхностную яркость (например, за счет мощной
вспышки звездообразования).
ослабевают
на 7 звездных величин (!). Следовательно, даже с помощью космических
наблюдений среди далеких галактик нам доступны лишь те, которые имеют
очень высокую поверхностную яркость (например, за счет мощной
вспышки звездообразования).
Падение яркости с увеличением ![]() (наряду с влиянием
(наряду с влиянием ![]() -поправки --
см. далее) приводит к еще одной наблюдательной
проблеме -- при сравнении линейных размеров галактик, наблюдаемых на разных
расстояниях, нельзя использовать их изофотные диаметры (то есть,
диаметры, измеренные в пределах фиксированного значения поверхностной
яркости). Для экспоненциального диска (43) при
-поправки --
см. далее) приводит к еще одной наблюдательной
проблеме -- при сравнении линейных размеров галактик, наблюдаемых на разных
расстояниях, нельзя использовать их изофотные диаметры (то есть,
диаметры, измеренные в пределах фиксированного значения поверхностной
яркости). Для экспоненциального диска (43) при ![]() радиус в пределах изофоты
радиус в пределах изофоты ![]() равен
равен
![]() (при
(при ![]() и
и
![]()
![]() ). Радиус диска, наблюдаемого на красном
смещении
). Радиус диска, наблюдаемого на красном
смещении ![]() , с использованием (98) может быть представлен как
, с использованием (98) может быть представлен как
![]() . Следовательно, уже при
. Следовательно, уже при ![]() изофотный радиус диска уменьшается на 0.38
изофотный радиус диска уменьшается на 0.38![]() или примерно на 10%
оптического радиуса. При
или примерно на 10%
оптического радиуса. При ![]() наблюдаемое изменение радиуса
достигает 2.8
наблюдаемое изменение радиуса
достигает 2.8![]() .
.
Для галактики, распределение яркости которой
описывается законом Вокулера (11), изменение изофотного
радиуса с ![]() дается следующей формулой:
дается следующей формулой:
![]() ,
где
,
где
![]() . Для
эллиптической галактики NGC 3379 с
. Для
эллиптической галактики NGC 3379 с
![]() (см. рис. 11)
изофотный радиус при
(см. рис. 11)
изофотный радиус при
![]() равен
равен
![]() .
При
.
При ![]() радиус галактики уменьшается до 2.70
радиус галактики уменьшается до 2.70![]() (на 14%),
а при
(на 14%),
а при ![]() -- до 0.89
-- до 0.89![]() .
.
При сравнении размеров галактик можно применять, например,
величины ![]() (для экспоненциального распределения) или использовать
подход, основанный на так называемой ''функции Петросяна''
[252]. Эта функция (точнее, величина ей обратная) равна
(для экспоненциального распределения) или использовать
подход, основанный на так называемой ''функции Петросяна''
[252]. Эта функция (точнее, величина ей обратная) равна
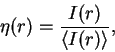 |
(99) |
Второй затрудняющий исследования фактор состоит в том, что при
наблюдении движущегося источника мы регистрируем в данном интервале
длин волн излучение, испущенное галактикой в другом -- смещенном --
диапазоне. Исправление наблюдений за этот эффект называется
![]() -поправкой.
Величина
-поправкой.
Величина ![]() -поправки в звездных величинах равна
-поправки в звездных величинах равна
В частном случае, когда распределение энергии в спектре
источника может быть описано степенным законом
![]() ,
формула (100) преобразуется в простое аналитическое
выражение (см., например, [254]):
,
формула (100) преобразуется в простое аналитическое
выражение (см., например, [254]):
.
У галактик с большими красными смещениями мы наблюдаем в оптическом
и ИК диапазонах излучение, испущенное в коротковолновой области спектра.
Например, излучение с
![]() Å от галактики с
Å от галактики с ![]() будет наблюдаться при
будет наблюдаться при ![]() в полосе
в полосе ![]() . Если эта галактика удалена
на
. Если эта галактика удалена
на ![]() , то ее УФ излучение будет фиксироваться в фильтре
, то ее УФ излучение будет фиксироваться в фильтре ![]() .
Основная проблема при учете
.
Основная проблема при учете ![]() -поправки состоит в том, что распределение
энергии в коротковолновой области спектров галактик известно плохо
и поэтому значение этой поправки для далеких галактик может быть
очень неточным. Кроме того, на наблюдаемое излучение галактик в
УФ диапазоне сильно влияет даже небольшое количество пыли. Объекты,
оптически тонкие в видимом диапазоне, могут быть оптически толстыми
в УФ.
-поправки состоит в том, что распределение
энергии в коротковолновой области спектров галактик известно плохо
и поэтому значение этой поправки для далеких галактик может быть
очень неточным. Кроме того, на наблюдаемое излучение галактик в
УФ диапазоне сильно влияет даже небольшое количество пыли. Объекты,
оптически тонкие в видимом диапазоне, могут быть оптически толстыми
в УФ.
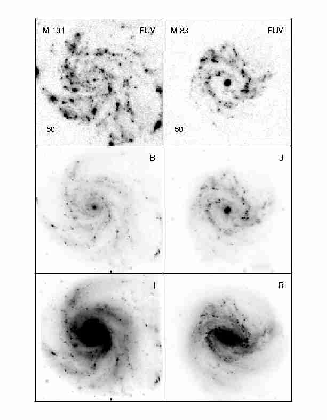 |
Большая роль относительного сдвига полос излучения и
приема при исследовании далеких объектов иллюстрируется
на рис. 50, где для двух близких спиральных галактик сравниваются изображения,
полученные в далекой ультрафиолетовой области спектра и в оптическом
диапазоне. Наглядно видно, что морфология и распределение поверхностной
яркости очень сильно меняются при смещении в УФ диапазон.
В [256] было выполнено моделирование того, как будут
выглядеть близкие галактики, если их отнести на разные ![]() , и показано,
что при оптических фотометрических наблюдениях объектов с
, и показано,
что при оптических фотометрических наблюдениях объектов с ![]() практически невозможно получить информацию об их истинных глобальных
характеристиках. Для компенсации этого эффекта необходимо проводить
наблюдения в более длинноволновой области спектра.
практически невозможно получить информацию об их истинных глобальных
характеристиках. Для компенсации этого эффекта необходимо проводить
наблюдения в более длинноволновой области спектра.
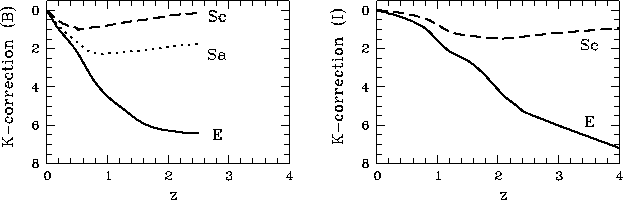 |
![]() -поправки для галактик разных морфологических типов
в фильтрах
-поправки для галактик разных морфологических типов
в фильтрах ![]() и
и ![]() согласно [257]
показаны на рис. 51 и приведены в Приложении (см. также [258]).
На рисунке видно, что относительный сдвиг полос излучения и
приема приводит к сильному занижению реальной светимости внегалактического
объекта.
Следует также обратить внимание на немонотонность значений поправок для
спиралей и их быстрый рост с изменением
согласно [257]
показаны на рис. 51 и приведены в Приложении (см. также [258]).
На рисунке видно, что относительный сдвиг полос излучения и
приема приводит к сильному занижению реальной светимости внегалактического
объекта.
Следует также обратить внимание на немонотонность значений поправок для
спиралей и их быстрый рост с изменением ![]() для
эллиптических галактик. Разное поведение
для
эллиптических галактик. Разное поведение ![]() для объектов
разных типов отражает значительные отличия в распределениях энергии
в их спектрах.
для объектов
разных типов отражает значительные отличия в распределениях энергии
в их спектрах.
![]() Поправка за эволюцию
Поправка за эволюцию
При интерпретации результатов фотометрического изучения далеких
галактик и сравнении их с характеристиками близких объектов необходимо
учитывать, что далекие объекты могут находится на более ранней стадии
своей эволюции. Фотометрическая структура галактик может эволюционировать
как за счет звездно-динамических процессов (например, [101]),
так и за счет эволюции характеристик составляющих их звезд.
Эллиптические галактики
При сильно упрощенном подходе эллиптическую галактику можно рассматривать как совокупность звезд, родившихся одновременно в ходе одиночной вспышки звездообразования. Приняв эту гипотезу, мы можем рассчитать светимость и показатели цвета галактики на любой момент времени (см. Приложение). Приведем, следуя в основном Тинсли [211], простую аналитическую модель эволюции фотометрических свойств эллиптической галактики.
Предположим, что галактика возникла в момент времени ![]() в ходе короткой одиночной вспышки звездообразования. Полная масса
всех звезд равна M
в ходе короткой одиночной вспышки звездообразования. Полная масса
всех звезд равна M![]() , их химический состав близок к солнечному.
Начальная функция масс (НФМ) родившихся звезд описывается степенным законом
, их химический состав близок к солнечному.
Начальная функция масс (НФМ) родившихся звезд описывается степенным законом
![]() , где
, где ![]() -- масса звезд вблизи
точки поворота с главной последовательности (ГП) в момент времени
-- масса звезд вблизи
точки поворота с главной последовательности (ГП) в момент времени ![]() .
Время жизни звезд на ГП (
.
Время жизни звезд на ГП (![]() ) связано с их массой выражением
) связано с их массой выражением
![]() (
(
![]() ).
Светимость может быть выражена через соотношение масса-светимость:
).
Светимость может быть выражена через соотношение масса-светимость:
![]() , где
, где
![]() .
Полная светимость галактики в первом приближении может быть представлена
как сумма светимостей звезд, находящихся на ГП, (карликов) и гигантов:
.
Полная светимость галактики в первом приближении может быть представлена
как сумма светимостей звезд, находящихся на ГП, (карликов) и гигантов:
![]() .
.
Через время ![]() после вспышки звездообразования на ГП остаются только
звезды в интервале масс от
после вспышки звездообразования на ГП остаются только
звезды в интервале масс от ![]() (нижняя граница НФМ) до
(нижняя граница НФМ) до ![]() (масса
точки поворота). Число таких звезд в интервале масс
(масса
точки поворота). Число таких звезд в интервале масс
![]() равно
равно
Используя (101) и (102) и введенные ранее аппроксимации,
можно найти интегральные массы и светимости гигантов и звезд на ГП.
Так, например, отношение полной массы гигантов к массе карликов
со временем увеличивается, но не превышает величины ![]() .
Следовательно, вклад гигантов в полную звездную массу галактики
пренебрежим.
.
Следовательно, вклад гигантов в полную звездную массу галактики
пренебрежим.
Полная светимость звезд на ГП при ![]() составляет
составляет
Отношение светимостей гигантов и звезд на ГП может быть представлено в следующем виде:
Подставив в (105) реалистические значения параметров, получаем, что в коротковолновой (голубой) области спектра
Оценим темп эволюции интегральной светимости эллиптической галактики.
Полная светимость может быть представлена как
Второе слагаемое в правой части (107) гораздо меньше первого (см. [211]) и поэтому
Следовательно, в первом приближении темп эволюции светимости эллиптических галактик (
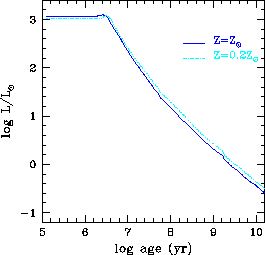
Проведенное выше элементарное рассмотрение приближенно согласуется с
результатами детальных численных расчетов эволюции фотометрических
характеристик эллиптических галактик [211]. На рис. 52
для примера показано изменение со временем болометрической светимости
родившихся в ходе одиночной вспышки звездообразования звезд для
двух значений металличности. При ![]() лет падение светимости
в логарифмических координатах происходит почти по линейному закону.
За время от
лет падение светимости
в логарифмических координатах происходит почти по линейному закону.
За время от ![]() лет после вспышки звездообразования до
лет после вспышки звездообразования до ![]() лет полная светимость уменьшается более, чем на 4
лет полная светимость уменьшается более, чем на 4![]() .
.
 |
Показатели цвета звезд, родившихся в ходе одиночной вспышки
звездообразования, со временем увеличиваются (становятся краснее).
Как видно из приведенных в Приложении таблиц, цвета реальных
эллиптических галактик при ![]() соответствуют показателям цвета звезд
с возрастом
соответствуют показателям цвета звезд
с возрастом ![]() лет.
лет.
Спиральные галактики
Спиральные галактики сложнее эллиптических и их нельзя описать в виде однородного по возрасту звездного населения. Процесс звездообразования в спиралях продолжается на протяжении всей их эволюции и поэтому в любой момент они представляют собой смесь звездных населений разных возрастов. При анализе фотометрической эволюции спиральных галактик в модели необходимо закладывать историю звездообразования (обычно рассматривается постоянная скорость звездообразования или затухающая со временем по экспоненциальному закону). В этом случае нельзя использовать простые соображения, использованные для анализа эллиптических галактик, и такие объекты можно изучать только на основе численного моделирования [211].
Величины эволюционных поправок для спиральных галактик, также как
и для эллиптических, могут достигать нескольких звездных величин
(например, [257]) и, следовательно, они сравнимы с ![]() -поправкой
и коррекцией за космологическое ослабление поверхностной яркости
(правда, эволюционная поправка имеет другой знак -- далекие, то есть
более молодые, объекты являются более яркими).
-поправкой
и коррекцией за космологическое ослабление поверхностной яркости
(правда, эволюционная поправка имеет другой знак -- далекие, то есть
более молодые, объекты являются более яркими).
В заключение этого раздела следует упомянуть еще два относительно
слабо изученных фактора, затрудняющих интерпретацию наблюдений
далеких объектов. Первый фактор -- это поглощение в межгалактической
среде. Второй -- ослабление излучения за счет поглощения в дисках
проектирующихся на луч зрения галактик. Поглощение в дисках фоновых
галактик не является серъезной проблемой при наблюдениях близких
объектов. Согласно приведенным в [260] расчетам, за счет
этого эффекта в полосе ![]() теряется не более 5% излучения от
галактики, находящейся при
теряется не более 5% излучения от
галактики, находящейся при ![]() (эта оценка зависит от принятой
космологической модели). Однако для галактики на
(эта оценка зависит от принятой
космологической модели). Однако для галактики на ![]() эта доля
увеличивается до
эта доля
увеличивается до ![]() 30%.
30%.
<< 9.1 Полезные формулы | Оглавление | 9.3 Результаты изучения ... >>
|
Публикации с ключевыми словами:
Фотометрическая система - слабые галактики - Скопление галактик - фотометрия
Публикации со словами: Фотометрическая система - слабые галактики - Скопление галактик - фотометрия | |
См. также:
Все публикации на ту же тему >> | |
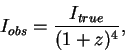
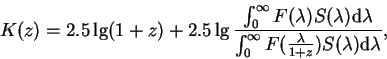
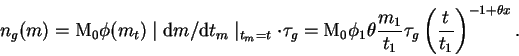
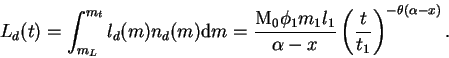
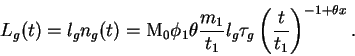
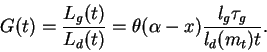
![\begin{displaymath}
L(t) = [1 + G(t)] L_d(t) =
\frac{{\rm M}_0 \phi_1 m_1 l_1}{\...
...a - x} (1+G) \left(\frac{t}{t_1}\right)^{-\theta(\alpha - x)}.
\end{displaymath}](https://images.astronet.ru/pubd/2006/08/23/0001215351/img986.gif)