Лекция 15. Построение модели Галактики
15.5. Интегральные уравнения звёздной статистики
Как упоминалось выше, для проверки точности моделей Галактики можно использовать звёздные подсчёты. В последние десятилетия звёздные подсчёты возродились вновь в связи с появлением мощных телескопов с автоматизированной обработкой результатов наблюдений. Использовать звёздные подсчёты для проверки моделей Галактики можно с помощью так называемых интегральных уравнений звёздной статистики, окончательный вид которых получил в начале ХХ-го века Шварцшильд.
Пусть мы наблюдаем область неба в телесном угле ω. Объем пространства с расстояниями от наблюдателя от r до r+dr будет равен ωr2dr, а число звёзд с видимыми величинами m тогда будет равно

|
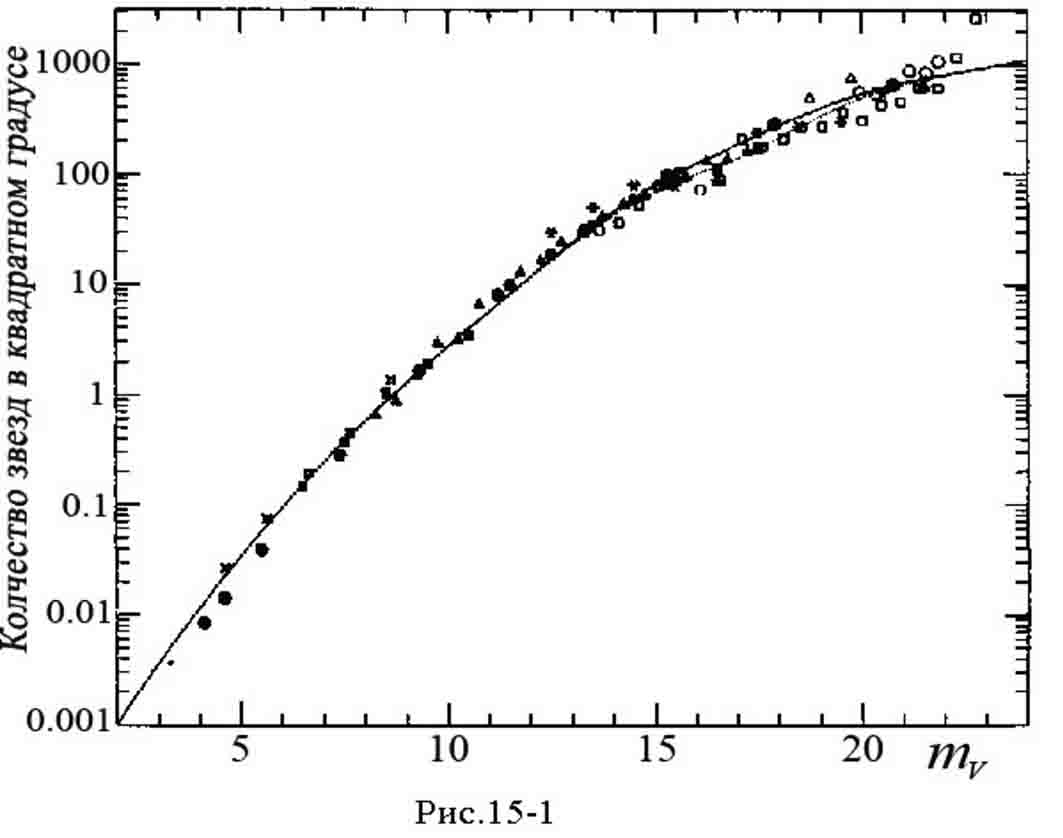
В настоящее время интегральные уравнения звёздной статистики используются для решения обратной задачи - по звёздной плотности из данной модели Галактики с помощью известной функции светимости получают расчётную функцию блеска, которая сравнивается с наблюдаемой в данном направлении. При этом для сравнения выбираются области, где поглощение света заведомо мало, в частности направление на галактические полюсы и окна прозрачности. Пример такого сравнения приведен на рис. 15-1. Здесь результаты звёздных подсчётов (функция блеска) в направлении галактического полюса (точки) сравниваются с предсказанной функцией блеска, полученной на основе многокомпонентной модели Галактики Бакала и Сонейры (сплошные линии). Рисунок показывает отличное согласие результатов моделирования и наблюдательных данных, по крайней мере, до видимой звёздной величины V ≈ 20m.
|
Публикации с ключевыми словами:
звездная астрономия
Публикации со словами: звездная астрономия | |
См. также:
Все публикации на ту же тему >> | |