Лекция 11. Структура Галактики и типы населений
11.2 Звёздные подсчёты
В предыдущих лекциях мы рассмотрели пространственное распределение рассеянных и шаровых звёздных скоплений в Галактике. Однако большая часть массы Галактики собрана в отдельных звёздах, не связанных с крупными звёздными группировками. Основная информация о распределении звёзд в Галактике получена путем звёздных подсчётов. Фактически звёздные подсчёты явились первым методом исследования в звёздной астрономии.
Первым серьезным исследованием структуры Галактики были звёздные подсчёты Гершеля. При этом впервые было применено выборочное исследование методом звёздных черпков. Подсчитать все звёзды, увиденные Гершелем в телескоп, было невозможно, поэтому он выбрал сначала 1083 площадки диаметром около 15' в области -30° < δ < +45° . В них Гершель насчитал 177600 звёзд до 14m.5. Позднее Д. Гершель добавил еще 2299 площадок южного неба. Таблицы численностей звёзд в площадках в зависимости от значений координат на небе позволили сделать следующие выводы:
На основе подсчётов Гершель построил первую модель Галактики, имеющую сейчас чисто исторический интерес, с ней можно познакомиться в учебниках.
После Гершелей неоднократно проводились звёздные подсчёты, причем в разных областях неба определяли интегральную функцию блеска N(m) - число звёзд ярче m-ой звёздной величины, и дифференциальную функцию блеска A(m) - число звёзд в единичном интервале звёздных величин. Из данных определений следует связь между этими функциями:
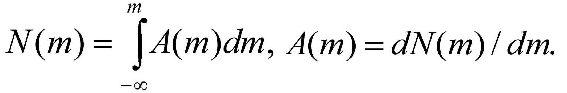
|
Возьмем звёзды одинаковой светимости. До некоторого расстояния r от наблюдателя все они будут ярче звёздной величины m. Звёзды слабее на 1m должны быть видны на расстоянии в 2.5121/2 ≈ 1.58 раза большим, что следует из основной формулы. Число наблюдаемых звёзд прямо пропорционально объему пространства, т.е.
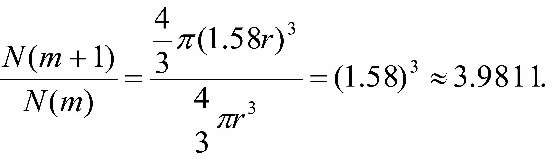
|
Опираясь на имевшиеся в то время результаты подсчётов звёзд, Зеелигер нашел, что во всех направлениях N(m) возрастает медленнее, чем по его теореме. (При этом оказалось, что более медленно число звёзд возрастает вне плоскости Млечного Пути.) В дальнейшем стало понятно, что отклонения поведения количества звёзд от теоремы Зеелигера вызывается главным образом существованием межзвёздного поглощения света.
Для получения представления о структуре Галактики и решения других вопросов звёздной астрономии Каптейн предложил план глубоких и всесторонних исследований звёзд в определенном числе выделенных площадок, распределенных по всему небу. До сих пор эти площадки, так называемые SA (selected areas) изучены лучше, чем лежащие между ними области неба, так как именно в этих областях на протяжении ХХ века гораздо чаще проводили фотометрию звёзд, определяли спектральные классы и лучевые скорости звёзд.
Сирс и ван-Райн в 1925 году провели звёздные подсчёты, использовав громадный материал астрографических каталогов <Карты неба> для подсчётов звёзд до 13m.5 и каталогов площадок Каптейна для продолжения этих подсчётов до 18m.5. Результаты подсчётов усредненные (сглаженные) по галактическим широтам и долготам частично показаны в таблице 11-2, где приведены величины lg N(m,b) до 21m.
Таблица 11-2
| m | lg N(m) | N(m+1)/N(m) | [N(m, 0º)]/[N(m, 90º)] | ||
| Все небо | b=00 | b=900 | |
||
| 4 | 2.553 | 2.88 | 2.88 | 2.88 | 3.4 |
| 5 | 3.012 | 2.85 | 2.85 | 2.85 | 3.4 |
| 6 | 3.468 | 2.80 | 2.82 | 2.77 | 3.4 |
| 7 | 3.916 | 2.77 | 2.80 | 2.70 | 3.4 |
| 8 | 4.358 | 2.72 | 2.77 | 2.60 | 3.6 |
| 9 | 4.793 | 2.67 | 2.75 | 2.50 | 3.9 |
| 10 | 5.220 | 2.61 | 2.70 | 2.39 | 4.3 |
| 11 | 5.635 | 2.54 | 2.67 | 2.29 | 4.8 |
| 12 | 6.041 | 2.47 | 2.62 | 2.17 | 5.6 |
| 13 | 6.433 | 2.39 | 2.55 | 2.06 | 6.8 |
| 14 | 6.811 | 2.31 | 2.46 | 1.97 | 8.4 |
| 15 | 7.173 | 2.22 | 2.35 | 1.87 | 10.4 |
| 16 | 7.520 | 2.12 | 2.23 | 1.77 | 13.2 |
| 17 | 7.847 | 2.03 | 2.13 | 1.68 | 16.6 |
| 18 | 8.155 | 1.93 | 2.04 | 1.60 | 21.0 |
| 19 | 8.439 | 1.84 | 1.93 | 1.51 | 27.0 |
| 20 | 8.704 | 1.76 | 1.84 | 1.43 | 34.4 |
| 21 | 8.949 | - | - | - | 44.2 |
Из второго столбца видно, насколько быстро возрастает число звёзд, которые можно видеть при увеличении проницающей силы телескопов. Последний столбец показывает резкое возрастание концентрации к плоскости Галактики все более слабых звёзд. Кроме того, подсчёты этих авторов показали увеличение численности звёзд в области центра Галактики и недостаток в области антицентра.
Широкие звёздные подсчёты дали возможность впервые оценить полное число звёзд в Галактике. Оказывается, что дифференциальная функция блеска хорошо представляется степенной зависимостью:
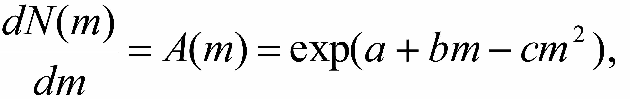
|
|
Публикации с ключевыми словами:
звездная астрономия
Публикации со словами: звездная астрономия | |
См. также:
Все публикации на ту же тему >> | |