Черные дыры в двойных звездных системах
12.12.2005 21:11 | "Соросовская Энциклопедия"
1. Введение
Черной дырой называется область пространства-времени, в которой гравитационное поле настолько сильно, что даже свет не может покинуть эту область. Это происходит, если размеры тела меньше его гравитационного радиуса rg,
Общая теория относительности А. Эйнштейна предсказывает удивительные свойства черных дыр, из которых важнейшее – наличие у черной дыры горизонта событий. Для невращающейся черной дыры радиус горизонта событий совпадает с гравитационным радиусом. На горизонте событий для внешнего наблюдателя ход времени останавливается. Космический корабль, посланный к черной дыре, с точки зрения далекого наблюдателя никогда не пересечет горизонт событий, а будет непрерывно замедляться по мере приближения к нему. Все, что происходит под горизонтом событий, внутри черной дыры, внешний наблюдатель не видит. Космонавт в своем корабле в принципе способен проникнуть под горизонт событий, но передать какую-либо информацию внешнему наблюдателю он не сможет. При этом космонавт, свободно падающий под горизонтом событий, вероятно, увидит другую Вселенную и даже свое будущее. Это связано с тем, что внутри черной дыры пространственная и временная координаты меняются местами и путешествие в пространстве здесь заменяется путешествием во времени. Еще более необычны свойства вращающихся черных дыр. У них горизонт событий имеет меньший радиус и погружен он внутрь эргосферы – такой области пространства-времени, в которой тела должны непрерывно двигаться, подхваченные вихревым гравитационным полем вращающейся черной дыры.
Столь необычные свойства черных дыр многим кажутся просто фантастическими, поэтому существование черных дыр в природе часто ставится под сомнение. Однако, согласно новейшим наблюдательным данным, черные дыры действительно существуют и им присущи удивительные свойства.
2. Как образуются черные дыры
Известно, что если масса ядра звезды, претерпевшего изменения химического состава из-за термоядерных реакций и состоящего в основном из элементов группы железа, превышает 1,4Mʘ (Mʘ – масса Солнца), но не превосходит 3Mʘ, то в конце ядерной эволюции звезды происходит коллапс (быстрое сжатие) ядра, в результате которого внешняя оболочка звезды, не затронутая термоядерными превращениями, сбрасывается, что наблюдается как вспышка сверхновой звезды. Коллапс приводит к формированию нейтронной звезды, в которой силам гравитационного притяжения противодействует градиент давления вырожденного нейтронного вещества. Огромные силы давления вырожденного нейтронного вещества обусловлены тем, что нейтроны обладают полуцелым спином и подчиняются принципу Паули, согласно которому в данном энергетическом состоянии может находиться только один нейтрон.
При сжатии ядра звезды, достигшей последней стадии эволюции, температура поднимается до гигантских значений, достигающих миллиарда кельвин, когда ядра атомов начинают разваливаться на протоны и нейтроны. Протоны поглощают электроны, превращаются в нейтроны, испуская при этом нейтрино. Нейтроны же, согласно квантово-механическому принципу Паули, при сильном сжатии начинают эффективно отталкиваться друг от друга. В случае, если масса коллапсирующего ядра меньше 3Mʘ, скорости нейтронов значительно меньше скорости света и упругость вещества, обусловленная в основном эффективным отталкиванием нейтронов, может уравновесить силы гравитации и привести к образованию устойчивых нейтронных звезд. В случае, если ядро звезды более массивно ( m>3Mʘ), то, согласно существующим представлениям, образующаяся нейтронная звезда остывая коллапсирует в черную дыру. Поскольку при образовании нейтронной звезды радиус ее ядра уменьшается от 106 до 10 км, из условия сохранения магнитного потока ( H0R02= HnRn2, где H0≈100 Э, R0≈106 км – соответственно напряженность магнитного поля и радиус ядра звезды до сжатия, а Hn, Rn – те же характеристики для нейтронной звезды) следует, что магнитное поле нейтронной звезды радиусом в 10 км может достигать очень больших величин, вплоть до 1012 Э, а плотность вещества – до миллиарда тонн в кубическом сантиметре. Такие нейтронные звезды проявляют себя как радиопульсары и рентгеновские пульсары. Радиопульсары наблюдаются как источники строго периодических (порядка секунд) импульсов радиоизлучения, возникающих при переработке энергии быстрого вращения звезды в направленное радиоизлучение через посредство сильного магнитного поля. Рентгеновские пульсары светят за счет аккреции вещества в тесных двойных звездных системах: сильное магнитное поле нейтронной звезды направляет плазму на магнитные полюсы, где она сталкивается с поверхностью нейтронной звезды и разогревается в ударной волне до температур в десятки и сотни миллионов кельвин. Это приводит к излучению рентгеновских квантов. Поскольку ось магнитного диполя не совпадает с осью вращения нейтронной звезды, рентгеновские пятна (их называют аккреционными колонками) при вращении нейтронной звезды то видны для земного наблюдателя, то экранируются телом нейтронной звезды, что приводит к эффекту маяка и феномену рентгеновского пульсара – строго периодической переменности рентгеновского излучения с периодами от долей секунды до тысяч секунд. Периодические пульсации радио- или рентгеновского излучения свидетельствуют о наличии у нейтронной звезды сильного магнитного поля, твердой поверхности и быстрого вращения. У черной дыры строго периодических пульсаций излучения ожидать не приходится, поскольку, согласно предсказанию общей теории относительности (ОТО), описывающей сильные гравитационные поля, черная дыра не имеет ни твердой поверхности, ни сильного магнитного поля.
Для звезд, массы железных ядер которых в конце эволюции превышают 3Mʘ, ОТО предсказывает неограниченное сжатие ядра (релятивистский коллапс) с образованием черной дыры. Это объясняется тем, что силы гравитации, стремящиеся сжать звезду, определяются плотностью энергии, а при громадных плотностях вещества, достигаемых при сжатии столь массивного ядра звезды, главный вклад в плотность энергии вносит уже не энергия покоя частиц, а энергия их движения и взаимодействия. Получается, что давление вещества при больших плотностях как бы само "весит": чем больше давление, тем больше плотность энергии и, следовательно, силы гравитации, стремящиеся сжать вещество. Кроме того, при сильных гравитационных полях, согласно ОТО, становятся принципиально важными эффекты искривления пространства-времени, что также способствует неограниченному сжатию ядра звезды.
Черные дыры с очень большими массами (до миллиардов солнечных масс), по-видимому, существуют в ядрах галактик. Кроме того, теория предсказывает возможность существования первичных черных дыр, возникших в момент образования Вселенной. Мы ограничимся рассмотрением лишь черных дыр звездной массы, образовавшихся на конечных этапах эволюции массивных (с массами в десятки солнечных) звезд.
3. Методы определения масс черных дыр
Известно, что массу звезды можно измерить, если она входит в двойную систему (см. статью А.А. Киселева "Двойные звезды" в этом томе). При этом, поскольку размеры орбиты двойной системы в миллионы раз больше гравитационных радиусов компонент, для определения масс звезд, в том числе масс нейтронных звезд и черных дыр в двойных системах, точность закона тяготения Ньютона вполне достаточна.
С бортов специализированных спутников открыты десятки тысяч компактных рентгеновских источников, большинство из которых представляют собой рентгеновские двойные системы – тесные двойные системы, состоящие из нормальной оптической звезды типа Солнца и релятивистского объекта, находящегося в режиме аккреции вещества (см. статью А.М. Черепащука "Тесные двойные звезды на поздних стадиях эволюции" в этом томе). Космические рентгеновские и наземные оптические наблюдения в данном случае прекрасно дополняют друг друга: наличие мощного рентгеновского источника (со светимостью в сотни тысяч раз превышающей болометрическую светимость Солнца) указывает на присутствие в двойной системе массивного объекта малых размеров (менее радиуса Земли), а спектральные и фотометрические наблюдения оптического спутника позволяют измерить массу релятивистского объекта. Если масса релятивистского объекта превышает 3Mʘ, его можно считать кандидатом в черные дыры. Число таких кандидатов в черные дыры в двойных системах с надежно измеренными массами достигло десяти и, благодаря успехам рентгеновской и оптической астрономии, непрерывно возрастает. Постепенно выясняется замечательный факт: ни один из известных десяти кандидатов в черные дыры не является рентгеновским пульсаром, то есть кандидаты в черные дыры отличаются от нейтронных звезд не только большими массами, но и наблюдательными проявлениями в полном соответствии с предсказаниями ОТО.
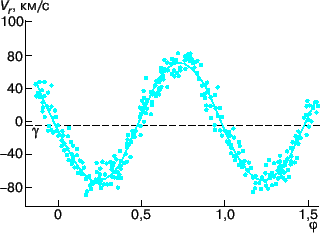 |
Рис. 1. Кривая лучевых скоростей системы Лебедь X-1, то есть зависимость от времени проекции на луч зрения скорости оптической звезды |
Опишем, как можно определить массу черной дыры в рентгеновской двойной системе. Наблюдения доплеровских смещений линий в спектре оптической звезды, вызванных ее орбитальным движением, позволяют построить кривую лучевых скоростей этой звезды, то есть зависимость от времени проекции вектора полной скорости звезды на луч зрения (см. рис. 1). Период, амплитуда и форма кривой лучевых скоростей определяют функцию масс оптической звезды:
| fo(m)= (mx sin i)3/(mx+mo)2 =1,038·10-7Ko3 P(1-e2 ) 3/2, | (1) |
где mx, mo – массы релятивистского объекта и оптической звезды (в солнечных массах), Ko – наблюдаемая полуамплитуда кривой лучевых скоростей оптической звезды (в км/с), P – орбитальный период (в сутках), e – эксцентриситет орбиты, i – наклонение орбиты системы (угол между нормалью к плоскости орбиты и лучом зрения). Функция масс оптической звезды fo(m) – это абсолютный нижний предел для массы релятивистского объекта mx . Значение массы релятивистского объекта (в нашем случае черной дыры) вычисляется по формуле
Величины q и i можно определить из анализа оптической кривой блеска рентгеновской двойной системы, из продолжительности затмения рентгеновского источника телом оптической звезды (в случае, когда наклонение орбиты i близко к 90°); для оценки этих параметров может служить также информация об отсутствии рентгеновских затмений, о расстоянии до системы и о вращательном уширении линий поглощения в спектре оптической звезды.
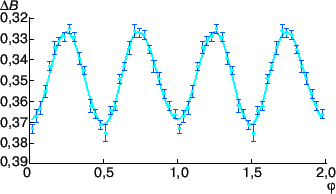 |
Рис. 2. Оптическая кривая блеска системы Лебедь X-1. Здесь φ – фаза орбитального периода, ΔB – разность в звездных величинах между Лебедь X-1 и звездой сравнения в синих лучах. Точки – данные наблюдений, сплошная линия – теоретическая кривая блеска, рассчитанная с учетом эффекта эллипсоидальности оптической звезды при оптимальных параметрах модели |
 |
Рис. 3. Кривая блеска рентгеновской Новой Мухи 1991 в неактивном состоянии, обусловленная в основном эффектом эллипсоидальности оптической звезды. Точки – данные наблюдений, сплошная линия – теоретическая кривая блеска, соответствующая оптимальным параметрам модели |
Модель рентгеновской двойной системы, используемая при интерпретации ее оптической кривой блеска, учитывает четыре причины оптической переменности. Это, во-первых, эффект эллипсоидальности оптической звезды, он связан с деформацией ее формы в гравитационном поле релятивистского объекта; во-вторых, эффект "отражения", связанный с прогревом оптической звезды мощным рентгеновским излучением аккрецирующего релятивистского объекта и орбитальным движением компонент; в-третьих, взаимные затмения компонентов и, в-четвертых, прецессия аккреционного диска, окружающего релятивистский объект (аккреционный диск может быть наклонен к плоскости орбиты и медленно прецессировать. Тогда в разных орбитальных циклах вклад диска в суммарный поток будет различным). Эффекты эллипсоидальности и "отражения" были впервые обнаружены и использованы для оценки параметров q и i в рентгеновских двойных системах Лебедь Х-1 и Геркулес Х-1 советскими учеными В.М. Лютым, Р.А. Сюняевым и А.М. Черепащуком в 1972 году. Эти эффекты оказались типичными оптическими проявлениями рентгеновских двойных систем, они помогают осуществлять их надежную оптическую идентификацию: совпадение периодов и фаз оптической и рентгеновской переменности или совпадение рентгеновской и оптической вспышек доказывает достоверность отождествления. На рис. 2 и 3 представлены оптические кривые блеска двух рентгеновских двойных систем Лебедь Х-1 (рис. 2) и Новой Мухи 1991 (рис. 3) в неактивном состоянии, содержащих компактные звезды – кандидаты в черные дыры. На рис. 4 изображена компьютерная модель системы Новая Мухи 1991 для оптимальных значений ее параметров: q=16, i = 41°, mx =13Mʘ.
![\includegraphics[width=78mm]{pic4.eps}](https://images.astronet.ru/pubd/2005/12/12/0001210267/img34.gif) |
Рис. 4. Компьютерная модель системы Новая Мухи 1991, построенная для оптимальных параметров (см. текст). Оптическая звезда приливно деформирована и имеет грушевидную форму. Аккреционный диск вокруг черной дыры имеет большие относительные размеры |
4. Как отличить черные дыры от нейтронных звезд
Аккрецирующая черная дыра не должна проявлять себя как рентгеновский пульсар. У нее может наблюдаться лишь иррегулярная переменность рентгеновского излучения с характерными временами Δt ≈ rg /c ≈0,0001-0,001 с. И действительно, в рентгеновской двойной системе Лебедь Х-1, содержащей черную дыру с массой около 10Mʘ, в те периоды, когда рентгеновская светимость понижена, а рентгеновский спектр – жесткий и степенной, наблюдается быстрая иррегулярная переменность рентгеновского потока на временах порядка миллисекунды. Наблюдения, выполненные с бортов современных рентгеновских обсерваторий, таких, как ГИНГА, МИР-КВАНТ, ГРАНАТ, АСКА, показали, что рентгеновские спектры систем – кандидатов в черные дыры – систематически более жесткие, чем спектры аккрецирующих нейтронных звезд, и простираются до энергий в несколько мегаэлектронвольт.
Как уже отмечалось, аккрецирующая нейтронная звезда может проявлять себя как рентгеновский пульсар. Однако если нейтронная звезда обладает слабым магнитным полем (напряженностью менее 1010 Э) или если ее ось вращения "неудачно" ориентирована относительно земного наблюдателя, то при аккреции на такую нейтронную звезду регулярные пульсации рентгеновского излучения могут и не наблюдаться . Поэтому отсутствие строго периодических пульсаций рентгеновского излучения нельзя считать строгим доказательством присутствия черной дыры в системе.
Однако при слабом магнитном поле нейтронной звезды и несильном темпе аккреции вещества на ее поверхности могут происходить термоядерные взрывы накопленного вещества, приводящие к коротким (длительностью ~1-10 с) и мощным вспышкам рентгеновского излучения. Такие объекты получили название рентгеновских барстеров 1-го типа (от английского слова burst – вспышка, взрыв). Барстерная переменность также является характерным признаком аккрецирующей нейтронной звезды, обладающей твердой поверхностью. Поскольку черная дыра не обладает твердой поверхностью, аккреция вещества на нее не должна приводить к феномену рентгеновского барстера 1-го типа. Отсутствие этого феномена также является лишь необходимым признаком присутствия в системе черной дыры. Таким образом, важнейшие признаки аккрецирующей черной дыры: мощное рентгеновское излучение, отсутствие феноменов рентгеновского пульсара или рентгеновского барстера 1-го типа и большая масса (более 3Mʘ). Среди этих четырех признаков надежное определение массы релятивистского объекта в рентгеновской двойной системе является решающим при идентификации его с черной дырой.
5. Новейшие данные
| п/п |
Рентгеновский источник |
fo(m),
Mʘ |
Масса релятивистского объекта, mx / Mʘ |
Масса оптической звезды, mo / Mʘ |
| 1 | Cyg X-1 (X-1 Лебедя) | 0,23 | 7-18 | 20-30 |
| 2 | LMC X-3 | 2,3 | 7-11 | 3-6 |
| 3 | LMC X-1 | 0,14 | 4-10 | 18-25 |
| 4 | A0620-00 (V616 Единорога) | 3,1 | 5-17 | ~0,7 |
| 5 | V404 Cyg (V404 Лебедя) | 6,3 | 10-15 | 0,5-1 |
| 6 | XN Mus (Новая Мухи) 1991 | 3,01 | 9-16 | 0,7-0,8 |
| 7 | QZ Vul (QZ Лисички) | 5,0 | 5,3-8,2 | ~0,7 |
| 8 | XN Per (Новая Персея) 1992 | 0,9 | 2,5-5 | ~0,4 |
| 9 | XN Sco (Новая Скорпиона) 1994 | 3,2 | 4-6 | ~2,3 |
| 10 | XN Oph (Новая Змееносца) 1997 | 4,0 | 5-7 | ~0,8 |
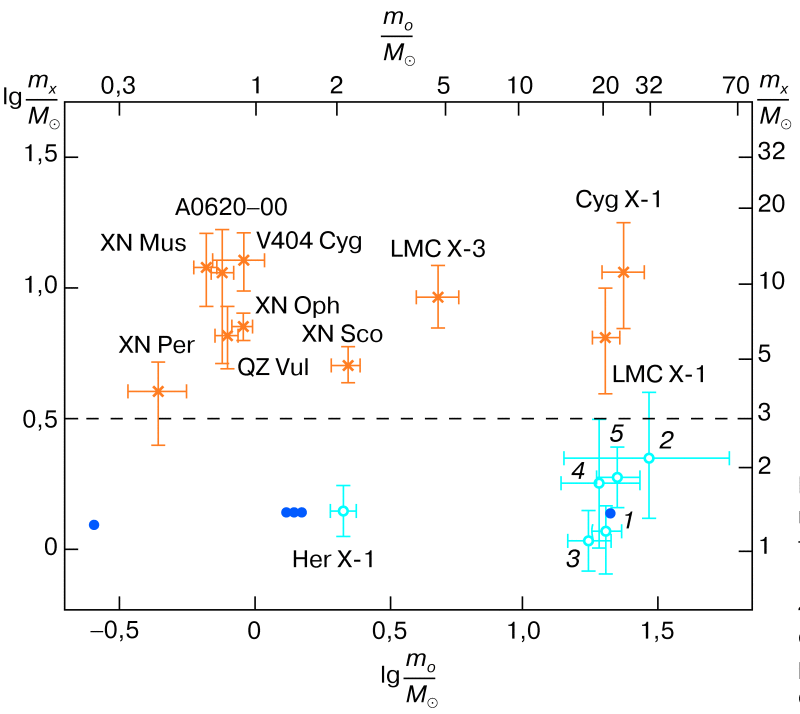 |
Рис. 5. Зависимость масс нейтронных звезд (кружки) и черных дыр (крестики) от масс спутников mo в тесных двойных системах. Цифрами обозначены 1 - система Cen X-3, 2 - LMC X-4, 3 - SMC X-1, 4 - 4U 1538-52, 5 - 4U 0900-40. Указаны ошибки определения масс. Темные кружки соответствуют радиопульсарам в двойных системах, ошибки определения масс которых менее размеров кружка. |
К настоящему времени в двойных системах измерены массы шести рентгеновских пульсаров и пяти радиопульсаров. Оказалось, что во всех случаях, когда удается надежно определить массу рентгеновского или радиопульсара (то есть нейтронной звезды), она не превосходит 3Mʘ, то есть теоретический верхний предел для массы нейтронной звезды, предсказываемый ОТО. Среднее значение массы нейтронной звезды, полученное для одиннадцати объектов, составляет около 1,4Mʘ и прекрасно согласуется с современной теорией поздних стадий эволюции массивных звезд.
Перейдем теперь к наиболее интригующему вопросу о том, как обстоят дела с массивными (с массами более 3Mʘ) рентгеновскими источниками. К настоящему времени известно десять рентгеновских двойных систем с массивными рентгеновскими источниками (табл. 1).
Надежность определения масс черных дыр mx в этих системах не вызывает сомнения, поскольку модель двойной системы в данном случае уверенно обоснована тем фактом, что в моменты минимумов блеска лучевая скорость оптической звезды совпадает с лучевой скоростью центра масс системы. Следовательно, изменения со временем лучевой скорости оптической звезды связаны с ее орбитальным движением, а не с пульсациями звезды или движением газовых потоков в системе. Применение мощных методов определения масс, развитых для тесных двойных систем, позволяет дать надежные оценки масс черных дыр.
Большие функции масс рентгеновских двойных систем пытались объяснить в рамках модели тройной системы. В этой модели рентгеновский источник – это аккрецирующая нейтронная звезда, а большая функция масс связана с движением оптической звезды вокруг третьей массивной звезды. Высокоточные спектроскопические исследования не выявили признаков тройственности ни у одной из десяти описанных выше рентгеновских двойных систем. Кроме того, в системах, где масса оптической звезды мала (менее одной-двух Mʘ), модель тройной системы неприемлема уже потому, что третья звезда должна иметь массу в несколько солнечных и на ее ярком фоне невозможно было бы наблюдать линии поглощения слабой маломассивной оптической звезды. Таким образом, к настоящему времени проблема черных дыр имеет прочный наблюдательный базис.
На рис. 5 приведены массы релятивистских объектов в зависимости от масс спутников в двойных системах. Спутниками рентгеновских пульсаров и черных дыр в двойных системах являются оптические звезды спектральных классов М-О. Спутники радиопульсаров – неактивные нейтронные звезды (например, система PSR 1913+16), белые карлики (PSR 1855+09), а также массивные звезды спектрального класса В (PSR 1259-63). Как видно на рисунке, масса релятивистских объектов не зависит от масс спутников. И нейтронные звезды, и черные дыры встречаются в двойных системах со спутниками как большой, так и малой массы. Ситуация здесь подобна той, которая имеет место в классических тесных двойных звездных системах, где встречаются любые комбинации компонент.
В тех случаях, когда спутником является массивная горячая оптическая звезда спектрального класса О или В (системы Лебедь X-1, LMC X-3, LMC X-1), рентгеновский источник квазистационарный. Во всех системах, у которых спутники – маломассивные холодные звезды поздних спектральных классов, рентгеновский источник является транзиентным (рентгеновской новой): в основном, спокойном, состоянии его рентгеновская светимость мала (менее 1033 эрг·с-1), однако раз в несколько десятков лет наблюдается явление рентгеновской новой, когда рентгеновская светимость увеличивается в миллионы раз и затем с характерным временем порядка нескольких месяцев спадает до фонового уровня. Эта корреляция между характером нестационарности рентгеновского источника и массой спутника – оптической звезды – должна обязательно учитываться при построении теории нестационарной дисковой аккреции на черные дыры.
Следует подчеркнуть очень важный наблюдательный факт: ни у одного из десяти массивных (с массой более 3Mʘ) рентгеновских источников – кандидатов в черные дыры – не обнаружено феноменов рентгеновского пульсара или рентгеновского барстера 1-го типа, характерных для аккрецирующих нейтронных звезд. Этот факт имеет фундаментальное значение и может рассматриваться как наблюдательный аргумент (но, разумеется, еще не как окончательное доказательство) в пользу того, что указанные в табл. 1 десять кандидатов в черные дыры действительно являются черными дырами в смысле ОТО.
6. Заключение
Мы описали астрономические методы и результаты определения масс черных дыр в рентгеновских двойных системах в основном из оптических исследований. Значения масс большого числа нейтронных звезд и черных дыр подтверждают справедливость предсказаний ОТО А. Эйнштейна. Новейшие наблюдательные данные по черным дырам, изложенные выше, имеют принципиальное значение для фундаментальной физики и релятивистской астрофизики, а также для теории внутреннего строения звезд и звездной эволюции. В последние годы в проблеме поиска и наблюдательных исследований черных дыр произошла "тихая" революция и гипотеза черных дыр во Вселенной превратилась в наблюдательную реальность. Это, несомненно, означает качественно новый этап в исследованиях черных дыр и их удивительных свойств, что в ближайшем будущем должно привести к значительному прогрессу в этой увлекательной области исследований.
Литература
|
Публикации с ключевыми словами:
черные дыры - функция масс - двойные системы - барстер - кандидаты в черные дыры
Публикации со словами: черные дыры - функция масс - двойные системы - барстер - кандидаты в черные дыры |

|
См. также:
Все публикации на ту же тему >> | |