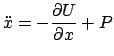Современное состояние теории движения искусственных спутников Земли
Т.В.Бордовицына
Томский Государственный Университет
Дается краткое описание современного состояния теории движения искусственных спутников Земли (ИСЗ). Рассматриваются аналитические и численные методы моделирования движения ИСЗ. Сопоставляются возможности существующих теорий движения и потребностей их практического применения.
|
Настоящая лекция является своеобразным представлением учебного пособия автора на тему "Теория движения искусственных спутников Земли. Аналитические и численные методы". Эта книга написана для того, чтобы дать студентам, специализирующимся в области небесной механики и космической геодезии, учебное пособие, охватывающее если не все, то хотя бы большинство методов и подходов, используемых для построения аналитических и численных моделей движения ИСЗ.
За 45 лет существования раздела науки, именуемого динамикой ИСЗ, создано много новых методов и алгоритмов, предназначенных как для приближенного, так и для высокоточного моделирования движения, написаны подробные монографии и аналитические обзоры, но учебников практически нет. Вышедшая в 1965 г. книга П. Е. Эльясберга "Введение в теорию полета искусственных спутников Земли", которую можно было бы порекомендовать студентам для первоначального ознакомления с проблемой, давно стала библиографической редкостью. А по современным результатам нет даже сколько-нибудь подробных обзоров. Подготовкой настоящего пособия мы попытались ликвидировать этот пробел.
С математической точки зрения задача о движении искусственного спутника Земли, как и задача о движении любого естественного объекта Солнечной системы, является задачей Коши. Движение описывается обыкновенными дифференциальными уравнениями с начальными условиями.
Обычно движение искусственного спутника Земли представляется как
движение материальной частицы бесконечно малой массы в поле
тяготения центрального тела с массой ![]() под действием сил,
определенных потенциальной функцией
под действием сил,
определенных потенциальной функцией ![]() , и совокупности
непотенциальных сил
, и совокупности
непотенциальных сил ![]() . В этом случае дифференциальные
уравнения движения частицы в прямоугольной инерциальной системе
координат, связанной с центральным телом
. В этом случае дифференциальные
уравнения движения частицы в прямоугольной инерциальной системе
координат, связанной с центральным телом ![]() , можно записать
следующим образом:
, можно записать
следующим образом:
с начальными условиями
| (2) |
где
Как аналитический, так и численный подходы к решению уравнений небесной механики основаны на приближении решений отрезками каких-либо рядов, однако в построении этих решений есть принципиальная разница.
Аналитический подход позволяет строить ряды, аппроксимирующие решение на значительных интервалах времени от одного до нескольких тысяч оборотов объекта. Кроме того, очень существенно, что аналитическая аппроксимация хотя и может зависеть от типа орбиты, но никогда напрямую не связана с начальными условиями уравнений движения. В связи с этим аналитическую аппроксимацию можно считать общим решением. И именно поэтому аналитические методы иногда называют методами общих возмущений.
Главная трудность при аналитическом подходе состоит в представлении правых частей уравнений движения в виде явных функций времени. Это достигается путем разложения возмущающей функции в ряд пуассоновского типа. Сложность построения точных аналитических аппроксимаций решения уравнений (1) приводит к тому, что более или менее общее решение, приемлемое для различных типов орбит, построить практически невозможно и применение каждой отдельной теории движения ограничено конкретным классом орбит.
При численном подходе к решению уравнений движения аппроксимация ищется в виде различных модификаций отрезка ряда Тейлора на интервале времени, существенно меньшем одного оборота. Коэффициенты разложения, что очень важно, вычисляются, исходя из начальных условий уравнений движения; и полученное решение является частным. Поэтому численные методы называют иногда методами специальных или частных возмущений. В то же время способ построения численных решений очень мало зависит от особенностей рассматриваемой орбиты, и численные модели движения строятся обычно для всего диапазона типов орбит ИСЗ.
При численном подходе к решению уравнений (1) существенными становятся некоторые общие свойства этих уравнений. Так, сингулярность уравнений (1) в окрестности начала координат для орбит, имеющих большие эксцентриситеты, приводит к сильным и неравномерным изменениям функций правых частей уравнений движения, что при применении численного метода требует постоянного изменения шага интегрирования и, как следствие, ведет к непроизводительным затратам компьютерного времени. Кроме того, решения уравнений (1) неустойчивы по Ляпунову даже в невозмущенном случае. Эта особенность, совершенно несущественная с точки зрения построения аналитического решения, в численном интегрировании приводит к усилению ошибки усечения аппроксимирующей формулы метода.
В докладе мы рассмотрим оба подхода к задаче моделирования движения ИСЗ, обсудим специфические особенности каждого подхода и приведем простые примеры. Кроме того, мы дадим обзор современных высокоточных аналитических и численных моделей движения ИСЗ и обсудим возможности их практического применения.
|
Публикации с ключевыми словами:
спутник
Публикации со словами: спутник | |
См. также:
Все публикации на ту же тему >> | |