Bibliography >>

ФОРМИРОВАНИЕ И ЭВОЛЮЦИЯ
Согласно современным представлениям (см., например, обзор Ларсона [1]), большинство одиночных и двойных звезд могло сформироваться при распаде неиерархических кратных звезд. Такие объекты образуются при фрагментации ядер молекулярных облаков (см., например, Клессен и др. [2]). Несмотря на огромное количество работ по теории звездообразования и по наблюдениям областей звездообразования, до сих пор нет какой-либо "стандартной" модели звездообразования [1]. По-видимому, формирующиеся малые группы звезд обладают широким диапазоном характеристик (размеров, дисперсий скоростей, спектров масс и т. д.).
На начальной стадии эволюции таких систем основную роль играют газодинамические процессы, которые можно описать в рамках SPH-схемы (см., например, обзор Боденхеймера и др. [3], а также статью Монахана [4]). Другой эффективный подход -- решение гидродинамических уравнений методом сеток с использованием кратных сеток или адаптивного "рафинирования" ячеек (AMR) (см. ссылки в том же обзоре [3]). В AMR-схеме в динамическом режиме меняются положения и размеры сеток, по мере необходимости создаются новые сетки и удаляются ненужные.
Численное моделирование процесса формирования звездных систем
показывает, что могут образовываться системы различной кратности с
характерными размерами
![]() а. е. В конце 60-х гг.
прошлого века ван Альбада [5] предположил, что устойчивые
двойные и кратные звезды могли сформироваться в результате
динамического распада малых звездных групп, содержащих от
нескольких до нескольких десятков звезд.
а. е. В конце 60-х гг.
прошлого века ван Альбада [5] предположил, что устойчивые
двойные и кратные звезды могли сформироваться в результате
динамического распада малых звездных групп, содержащих от
нескольких до нескольких десятков звезд.
С другой стороны, иерархические устойчивые кратные звезды также могут формироваться из вращающегося газопылевого облака в результате фрагментации (см., например, обзор [3]).
Дальнейшая эволюция системы может быть описана в рамках
гравитационной задачи ![]() тел с учетом ряда дополнительных
эффектов -- слияний компонентов при тесных сближениях, приливных
взаимодействий звезд, потери массы компонентами вследствие
звездного ветра и вспышечной активности. Пример динамической
эволюции неиерархической системы
тел с учетом ряда дополнительных
эффектов -- слияний компонентов при тесных сближениях, приливных
взаимодействий звезд, потери массы компонентами вследствие
звездного ветра и вспышечной активности. Пример динамической
эволюции неиерархической системы ![]() тел показан в следующем
фильме. Здесь мы видим сближения, выбросы и уходы звезд,
формирование двойных подсистем. В финале эволюции образуется
двойная или устойчивая иерархическая тройная система.
тел показан в следующем
фильме. Здесь мы видим сближения, выбросы и уходы звезд,
формирование двойных подсистем. В финале эволюции образуется
двойная или устойчивая иерархическая тройная система.
Численные эксперименты (см., например, Стерзик и Дурисен [6],
Рубинов, Петрова и Орлов [7]) показывают, что неиерархические
системы малой кратности распадаются на динамически несвязанные
подсистемы. Это могут быть одиночные звезды, двойные, устойчивые
иерархические тройные и, возможно, системы большей кратности.
Рассмотрим распределение состояний кратных систем с
![]() и начальным спектром масс Солпитера на
момент времени 300
и начальным спектром масс Солпитера на
момент времени 300 ![]() , где
, где ![]() -- среднее начальное
время пересечения компонентом системы (табл. 1). Примерно в
половине случаев к этому моменту эволюция системы заканчивается
формированием двойной системы. Еще примерно в 10-15% случаев
образуется устойчивая тройная система. Около 30% систем к этому
моменту не завершили свою эволюцию.
-- среднее начальное
время пересечения компонентом системы (табл. 1). Примерно в
половине случаев к этому моменту эволюция системы заканчивается
формированием двойной системы. Еще примерно в 10-15% случаев
образуется устойчивая тройная система. Около 30% систем к этому
моменту не завершили свою эволюцию.
Интересно сопоставить результаты с функцией кратности наблюдаемых
звезд. По каталогу 807 физических кратных систем функцию кратности
построил Токовинин [8]. Он нашел отношения числа систем
разной кратности ![]() :
:
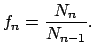
Отметим, что отношение ![]() в пределах ошибок примерно постоянно,
начиная с
в пределах ошибок примерно постоянно,
начиная с ![]() , и составляет
, и составляет
![]() . При переходе от
тройных к двойным оно уменьшается примерно вдвое (табл. 2).
. При переходе от
тройных к двойным оно уменьшается примерно вдвое (табл. 2).
Орлов и Титов [9] оценили отношение числа звезд, входящих в
системы кратности
![]() , для близких звезд в пределах
25 пк от Солнца как
, для близких звезд в пределах
25 пк от Солнца как
![]() . Соответствующие оценки
отношений
. Соответствующие оценки
отношений
![]() ,
,
![]() в пределах ошибок
согласуются с данными Токовинина [8]. Оценка
в пределах ошибок
согласуются с данными Токовинина [8]. Оценка
![]() для звезд окрестности Солнца согласуется с оценкой
для звезд окрестности Солнца согласуется с оценкой
![]() , полученной для процесса распада малых групп звезд.
, полученной для процесса распада малых групп звезд.
Если мы предположим, что неустойчивые тройные системы в конечном
счете распадаются с формированием финальной двойной, то доля
финальных двойных достигнет 70%. Соответствующее отношение
![]() не сильно отличается от оценок, полученных из
наблюдений. Сейчас мы не знаем, сколь часто формируются устойчивые
системы с кратностью
не сильно отличается от оценок, полученных из
наблюдений. Сейчас мы не знаем, сколь часто формируются устойчивые
системы с кратностью ![]() . По-видимому, часть систем с
. По-видимому, часть систем с ![]() неустойчивы и распадаются за время, большее 300
неустойчивы и распадаются за время, большее 300 ![]() ,
с образованием двойных или устойчивых тройных систем. Поэтому
оценка
,
с образованием двойных или устойчивых тройных систем. Поэтому
оценка
![]() ненадежна.
ненадежна.
Интересно определить характеристики финальных устойчивых систем и сравнить их с данными наблюдений двойных и тройных звезд.
Основные характеристики двойных звезд -- большая полуось и
эксцентриситет орбиты. При начальных размерах группы ![]() а. е. большие полуоси финальных и выброшенных двойных систем
находятся в диапазоне от
а. е. большие полуоси финальных и выброшенных двойных систем
находятся в диапазоне от ![]() до
до ![]() а. е. Этот
диапазон согласуется с данными для широких двойных (см., например,
Дюкенуа и Майор [10], Хикокс [11]). Более тесные двойные
в принципе могли сформироваться при динамическом распаде более
компактных групп звезд.
а. е. Этот
диапазон согласуется с данными для широких двойных (см., например,
Дюкенуа и Майор [10], Хикокс [11]). Более тесные двойные
в принципе могли сформироваться при динамическом распаде более
компактных групп звезд.
Распределения эксцентриситетов двойных, формирующихся при распаде
систем с кратностью ![]() и начальным спектром масс Солпитера,
приведены на рис. 1. Прямая соответствует закону
и начальным спектром масс Солпитера,
приведены на рис. 1. Прямая соответствует закону ![]() , полученному Амбарцумяном [12] для равновесного
распределения двойных в звездном поле. Такое же распределение
получено в статистической теории распада тройных систем (см.
Монахан [13]).
, полученному Амбарцумяном [12] для равновесного
распределения двойных в звездном поле. Такое же распределение
получено в статистической теории распада тройных систем (см.
Монахан [13]).
Из рисунка видно, что результаты численного моделирования согласуются
с теорией.
Распределения эксцентриситетов широких двойных звезд
после учета наблюдательной селекции также согласуются с законом
![]() (см., например, Валтонен [14], Токовинин [15]).
Это согласование является дополнительным аргументом
в пользу динамического происхождения широких двойных.
(см., например, Валтонен [14], Токовинин [15]).
Это согласование является дополнительным аргументом
в пользу динамического происхождения широких двойных.
Перейдем к рассмотрению устойчивых тройных систем.
Устойчивые тройные, образующиеся при распаде малых групп,
обладают значительной иерархией --
среднее отношение больших полуосей орбит внешней и внутренней двойных
составляет примерно ![]() , а среднее отношение периодов --
приблизительно
, а среднее отношение периодов --
приблизительно ![]() .
.
На рис. 2 представлены распределения эксцентриситетов внутренних и внешних двойных.
Из рисунка видно, что как для внутренних, так и для внешних пар
распределения эксцентриситетов отличаются от закона
![]() . Наблюдается дефицит сильно вытянутых орбит с
. Наблюдается дефицит сильно вытянутых орбит с ![]() . Особенно этот дефицит заметен для внешних двойных. Средние
значения эксцентриситетов составляют
. Особенно этот дефицит заметен для внешних двойных. Средние
значения эксцентриситетов составляют
![]() ,
,
![]() . Нами была рассмотрена
выборка 38 иерархических тройных звезд с известными элементами
орбит внутренней и внешней двойных. По этой выборке средние
значения эксцентриситетов
. Нами была рассмотрена
выборка 38 иерархических тройных звезд с известными элементами
орбит внутренней и внешней двойных. По этой выборке средние
значения эксцентриситетов
![]() ,
,
![]() . Эти значения
несколько меньше величин, полученных для модельных систем.
Особенно заметно различие для внутренних двойных. Это различие
может быть связано с частичной циркуляризацией орбит внутренних
двойных из-за приливного взаимодействия компонентов, которое не
учитывалось при численном моделировании. Кроме того, на результате
может сказаться селекция -- трудность обнаружения сильно
вытянутых систем.
. Эти значения
несколько меньше величин, полученных для модельных систем.
Особенно заметно различие для внутренних двойных. Это различие
может быть связано с частичной циркуляризацией орбит внутренних
двойных из-за приливного взаимодействия компонентов, которое не
учитывалось при численном моделировании. Кроме того, на результате
может сказаться селекция -- трудность обнаружения сильно
вытянутых систем.
Еще одна важная характеристика структуры иерархических тройных систем -- относительная ориентация орбит внутренней и внешней двойных. В наших моделях с первоначально изотропным распределением скоростей в финальных устойчивых тройных несколько преобладают системы с прямыми движениями (рис. 3).
Анализ распределения ![]() для устойчивых тройных, образующихся
при распаде систем с
для устойчивых тройных, образующихся
при распаде систем с
![]() звезд, был выполнен в
работе Стерзика и Токовинина [16]. Результат зависит от
геометрии системы, спектра масс, соотношения между энергией
вращения и энергией случайных движений компонентов. Для случаев с
близкими к изотропному распределениями начальных скоростей
финальные тройные показывают умеренное, но значимое преобладание
прямых движений со средними значениями угла между векторами
орбитальных моментов внешней и внутренней пар
звезд, был выполнен в
работе Стерзика и Токовинина [16]. Результат зависит от
геометрии системы, спектра масс, соотношения между энергией
вращения и энергией случайных движений компонентов. Для случаев с
близкими к изотропному распределениями начальных скоростей
финальные тройные показывают умеренное, но значимое преобладание
прямых движений со средними значениями угла между векторами
орбитальных моментов внешней и внутренней пар
![]() . Для наблюдаемых 22 тройных систем с
известными элементами орбит внутренней и внешней двойных (однако с
неопределенностью долгот восходящих узлов) получена усредненная
оценка угла
. Для наблюдаемых 22 тройных систем с
известными элементами орбит внутренней и внешней двойных (однако с
неопределенностью долгот восходящих узлов) получена усредненная
оценка угла
![]() . Эта оценка получена
по смеси верных и ложных углов. Тем не менее видны явная
некомпланарность орбит и тенденция к преобладанию систем с прямыми
движениями. Эта оценка согласуется и с результатами наших
численных экспериментов [7].
. Эта оценка получена
по смеси верных и ложных углов. Тем не менее видны явная
некомпланарность орбит и тенденция к преобладанию систем с прямыми
движениями. Эта оценка согласуется и с результатами наших
численных экспериментов [7].
Нами были выполнены численные эксперименты с другим начальным спектром масс, менее крутым, чем спектр масс Солпитера. Также были рассмотрены разные начальные размеры систем -- от 3 до 1000 а. е. и разные начальные значения вириального отношения -- от 0.001 до 0.9.
Выяснилось, что имеются некоторые инвариантные свойства финальных систем
- Высокая доля устойчивых тройных (10-15%).
- Универсальность распределения эксцентриситетов финальных и уходящих
двойных
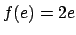 .
.
- Значительная иерархия финальных тройных.
- Внешние двойные имеют менее вытянутые орбиты,
чем внутренние.
- Преобладание тройных систем с прямыми движениями.
На динамическую эволюцию кратных звезд могут влиять некоторые дополнительные факторы, в частности:
1) динамическое трение звезд о межзвездную среду,
2) потеря массы звездами,
3) приливное взаимодействие звезд при тесных сближениях.
Нами были рассмотрены первые два эффекта. Для реалистичных оценок плотности межзвездной среды и темпа потери массы результаты оказываются практически теми же, что и без учета этих эффектов.
Потеря массы за счет звездного ветра сказывается на динамической
эволюции широких кратных систем с характерными начальными
размерами ![]() а. е. Финальные двойные и тройные становятся
в среднем более широкими. При этом внешние двойные в устойчивых
тройных системах в среднем становятся более вытянутыми.
а. е. Финальные двойные и тройные становятся
в среднем более широкими. При этом внешние двойные в устойчивых
тройных системах в среднем становятся более вытянутыми.
Теперь рассмотрим эволюцию двойных и иерархических тройных систем, которые могут формироваться как при распаде малых групп, так и при фрагментации вращающегося протозвездного облака.
Широкие двойные системы сохраняют стабильность, если они достаточно изолированы от звезд поля. В тесных двойных с обменом веществом между компонентами возможно слияние звезд. В результате образуются объекты, которые называются голубыми бродягами. В более широких двойных приливное взаимодействие компонентов приводит к циркуляризации орбит, синхронизации вращения компонентов с орбитальным движением и ортогонализации осей вращения звезд к плоскости орбиты.
Приливное взаимодействие звезд, потеря массы и обмен веществом между компонентами могут повлиять на динамическую эволюцию иерархических тройных систем, находящихся вблизи границы устойчивости.
Оказалось (см. Орлов и Петрова [17]), что влияние приливов на изменение параметров устойчивости тройных систем зависит от вращения звезд. Если ротационные скорости звезд превышают синхронизованные с орбитальным движением, то запас устойчивости тройной системы уменьшается. В противном случае он возрастает.
Эффект потери массы посредством звездного ветра несколько сложнее. Здесь следует рассмотреть два сценария нарушения устойчивости тройной системы:
- Обмен компонентами -- нарушение иерархической структуры системы.
- Уход удаленного компонента без предшествующего нарушения
иерархии.
Оказалось (Орлов, Петрова и Иванова [18]), что потеря массы звездами приводит к повышению запаса устойчивости тройной системы по отношению к нарушению иерархии. Что касается ухода удаленной звезды без нарушения иерархии, то результат зависит от отношения масс компонентов. Если масса удаленного компонента меньше, чем суммарная масса внутренней двойной, то имеет место тенденция к потере устойчивости. В противном случае наблюдается увеличение запаса устойчивости. Следует отметить, что характерные времена изменения меры устойчивости сравнимы с эволюционными временами компонентов.
Можно рассмотреть также эффект обмена веществом в тесной паре (Петрова [19]). Изменение запаса устойчивости зависит от того, какой из компонентов тесной пары теряет вещество. Если массу теряет более массивный компонент пары, то двойная становится более тесной и запас устойчивости тройной системы увеличивается. Если массу теряет более легкий компонент пары, то двойная становится шире и запас устойчивости уменьшается. Гравитационные возмущения со стороны третьего удаленного компонента приводят к некоторым нерегулярностям в зависимостях изменений параметров устойчивости со временем - зависимости часто имеют вид ступенек. Наиболее сильные изменения параметров устойчивости происходят вблизи перицентра внешней двойной.
В заключение заметим, что в принципе при фрагментации газовых облаков могут формироваться как неиерархические динамически неустойчивые, так и иерархические устойчивые кратные системы. В первом случае система распадается на устойчивые двойные и кратные подсистемы и одиночные звезды. Время распада обычно на несколько порядков величины короче эволюционных времен компонентов. Во втором случае динамическая эволюция протекает значительно медленнее - характерные времена сравнимы с эволюционными временами компонентов.
Для дальнейших работ в этом направлении требуется, с одной стороны, накопление надежного статистического материала для тройных звезд и звезд большей кратности с известными орбитами внутренней и внешней пар (особенно оценки взаимного наклона орбит), а с другой стороны, необходимы достаточно ''рафинированные'' численные модели динамики малых групп звезд, а также алгоритмы объективного сравнения моделей и наблюдений.
Bibliography >>
|
Публикации с ключевыми словами:
кратные системы - двойные звезды - двойные системы - тройные системы - тройные звезды
Публикации со словами: кратные системы - двойные звезды - двойные системы - тройные системы - тройные звезды | |
См. также:
Все публикации на ту же тему >> | |