Черная дыра
1. Введение
2. Поле тяготения невращающейся
черной дыры
3. Поле тяготения вращающейся
черной дыры
4. Физические процессы
в поле тяготения черной дыры
1. Введение
Черная дыра - область пространства, в к-рой поле тяготения настолько сильно, что
вторая космич. скорость (параболическая
скорость)
для находящихся в этой области тел должна была бы превышать скорость света, т.е.
из Ч.д. ничто не может вылететь - ни излучение, ни частицы, ибо в природе ничто не
может
двигаться со скоростью, большей скорости света. Границу области, за к-рую не выходит
свет, наз. горизонтом Ч.д. Для того чтобы поле тяготения смогло "запереть" излучение,
создающее это поле масса ![]() должна сжаться до объема с радиусом,
меньшим гравитационного радиуса
должна сжаться до объема с радиусом,
меньшим гравитационного радиуса ![]() . Гравитац. радиус чрезвычайно мал даже для больших масс (напр., для
Солнца, имеющего массу
. Гравитац. радиус чрезвычайно мал даже для больших масс (напр., для
Солнца, имеющего массу ![]() г,
г, ![]() 3 км).
3 км).
Поле тяготения Ч.д. описывается теорией тяготения Эйнштейна (см. Тяготение). Согласно этой теории, вблизи Ч.д. геометрич. св-ва пространства описываются неевклидовой (римановой) геометрией, а время течет медленнее, чем вдали, вне сильного поля тяготения.
По совр. представлениям, массивные звезды (с массой в неск. ![]() и больше), заканчивая свою эволюцию, могут в конце концов сжаться (сколлапсировать)
и превратиться в Ч.д. (см. Эволюция звезд,
Гравитационный коллапс).
и больше), заканчивая свою эволюцию, могут в конце концов сжаться (сколлапсировать)
и превратиться в Ч.д. (см. Эволюция звезд,
Гравитационный коллапс).
Если Ч.д. возникает при сжатии невращающегося незаряженного тела, то ее внеш. поле
тяготения оказывается строго сферическим и зависящим только от полной массы тела
![]() . Все отклонения от сферичности в граивтац. поле при образовании Ч.д. излучаются
в виде гравитац. волн (см. Гравитационное
излучение). Оставшееся поле не зависит от распределения массы внутри сжавшегося
тела. Т.о., хотя внутри Ч.д. может быть "спрятано" очень несимметрично сжимающееся
тело,
внеш. поле тяготения будет строго сферически-симметричным (т.н. поле Шварцшильда).
. Все отклонения от сферичности в граивтац. поле при образовании Ч.д. излучаются
в виде гравитац. волн (см. Гравитационное
излучение). Оставшееся поле не зависит от распределения массы внутри сжавшегося
тела. Т.о., хотя внутри Ч.д. может быть "спрятано" очень несимметрично сжимающееся
тело,
внеш. поле тяготения будет строго сферически-симметричным (т.н. поле Шварцшильда).
При образовании Ч.д. излучаются также все физ. поля, кроме статического электрического поля (если коллапсирующее тело было электрически заряженным).
Если тело, образовавшее Ч.д., вращалось, то вокруг Ч.д. сохраняется "вихревое" гравитац. поле, увлекающее все тела вблизи Ч.д. во вращательное движение вокруг нее. Это поле определяется помимо массы Ч.д. только ее полным моментом импульса. Поле тяготения вращающейся Ч.д. наз. полем Керра.
2. Поле тяготения невращающейся черной дыры
Движение тел в поле тяготения Шварцшильда обладает рядом особенностей. В теории Ньютона
движение по окружности вокруг тяготеющего центра возможно на любом расстоянии R
от него. В теории Эйнштейна это не так. Чем ближе к Ч.д., тем больше скорость кругового
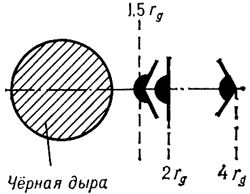
движения. На окружности с R=1,5 rg скорость
движения достигает световой. Ближе к Ч.д. движение по окружности, очевидно, вообще
невозможно. В действительности же движение по окружности становится неустойчивым
на значительно
больших расстояниях, а именно: начиная с R=3 rg,
когда скорость движения составляет всего половину световой. Только на расстояниях,
превышающих 3rg, возможно устойчивое круговое движение.
На пределе устойчивости круговых орбит энергия
связи частицы ![]() , где m - масса
частицы.
, где m - масса
частицы.
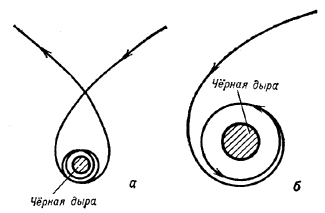
Особый интерес представляет возможность гравитац. захвата черной дырой тел, прилетающих из бесконечности к тяготеющей массе, описывает около нее параболу или гиперболу и (если не испытывает соударения с тяготеющей массой) снова улетает в бесконечность. Гравитац. захват в этой задаче невозможен.
|
| Рис. 1. |
Наконец, если тело подойдет вплотную к указанной окружности, то его орбита будет неограниченно навиватсья на окружность. Тело окажется гравитационно захваченным Ч.д. и никогда снова не улетит в космос (рис. 1, б). Если же тело подлетит еще ближе к Ч.д., то после неск. оборотов или даже не успев сделать ни одного оборота, оно упадет в Ч.д.
|
| Рис. 2. |
|
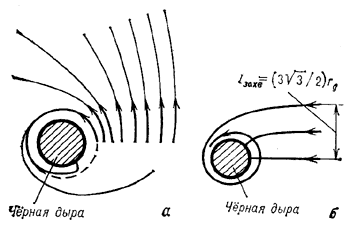
| Рис. 3. |
Наличие критич. окружности ведет к тому, что все лучи с прицельным параметром на
бесконечности ![]() гравитационно захватываются
(рис. 3, б).
гравитационно захватываются
(рис. 3, б).
3. Поле тяготения вращающейся черной дыры
Около вращающейся Ч.д., как уже было сказано, должно существовать "вихревое" гравитац. поле. Вдали от Ч.д. оно очень слабо, а вблизи возрастает настолько, что ведет к качественно новым эффектам.
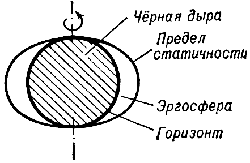
Так, в окрестности вращающейся Ч.д. возникает область, в к-рой все тела и фотоны увлекатся в движение вокург Ч.д. Внеш. граница этой области наз. пределом статичности. Однако внутри предела статичности тела и фотоны совсем не обязательно должны падать к центру, они могут и приближаться к Ч.д. и удаляться от нее, могут выходить за предел статичности. Т.о., предел статичности не явл. границей Ч.д., ее горизонтом, из-под к-рого нельзя выйти. Линейные размеры предела статичности по порядку величины равны rg. Горизонт Ч.д. расположен глубже, под пределом статичности. Пространство между горизонтом и пределом статичности наз. эргосферой (рис. 4). Предел статичности касается горизонта в полюсах вращающейся Ч.д.
При падении тела на вращающуюся Ч.д. оно сначала отклоняется в своем движении в сторону вращения Ч.д., пересекает границу эргосферы и постепенно приближается к горизонту. Для внеш. наблюдателя свет, испускаемый падающим телом, становится все более красным и менее интенсивным, затем полностью затухает: тело, уйдя под горизонт, становится невидимым для внеш. наблюдателя. На горизонте все тела имеют одну ту же угловую скорость обращения, в какое бы место горизонта ни попадало падающее тело.
Общая для всех падающих тел угловая скорость ![]() на горизонте Ч.д.
и есть скорость ее вращения:
на горизонте Ч.д.
и есть скорость ее вращения: ![]() , где I
-
момент импульса тела, из к-рого возникла Ч.д.,
, где I
-
момент импульса тела, из к-рого возникла Ч.д., ![]() - масса,
S - площадь горизонта Ч.д. Момент импульса Ч.д. заданной массы не может быть
сколь
угодно большим. Максимально возможные значения I и
- масса,
S - площадь горизонта Ч.д. Момент импульса Ч.д. заданной массы не может быть
сколь
угодно большим. Максимально возможные значения I и ![]() определяются тем, что при образовании Ч.д. линейная скорость вращения точек экватора
тела
не превышает скорости света. По порядку величины
определяются тем, что при образовании Ч.д. линейная скорость вращения точек экватора
тела
не превышает скорости света. По порядку величины ![]() .
Для Ч.д. с массой, равной массе Солнца,
.
Для Ч.д. с массой, равной массе Солнца, ![]() (1/с).
(1/с).
|
| Рис. 4. |
Рассмотрим для примера захват фотона, движущегося в плоскости экватора максимально быстро вращающейся Ч.д.
Для фотона, движущегося в направлении вращения Ч.д., прицельный параметр lзахв,1=1/2
rg; для фотона, движущегося
против вращения, прицельный параметр намного больше: lзахв,2=4
rg. Изменяется ситуация и с круговыми орбитами.
Для Ч.д. без вращения последняя устойчивая круговая орбита имеет радиус 3rg;
частица, движущаяся по ней, имеет скорость c/2. И самое
важное: чтобы попасть на эту орбиту, частица с массой m должна отдать энергию
![]() (энергию связи) в виде, напр., гравитационного
излучения.
(энергию связи) в виде, напр., гравитационного
излучения.
В случае максимально быстро вращающейся дыры последняя круговая орбита лежит в экваториальной
плоскости близко к горизонту, глубоко внутри эргосферы. Но здесь частица может
двигаться только в сторону вращения Ч.д. Энергия, к-рую выделяет частица, попавшая
на эту орбиту, гораздо больше и составляет ![]() .
В то
же время последняя устойчивая орбита частицы, обращающейся вокруг дыры в противоположном
направлении, лежит вне эргосферы и частица, попадающая в нее, выделяет энергию
.
В то
же время последняя устойчивая орбита частицы, обращающейся вокруг дыры в противоположном
направлении, лежит вне эргосферы и частица, попадающая в нее, выделяет энергию ![]() .
.
Полная масса вращающейся Ч.д. определяется как ее размерами (площадью S горизонта),
так и энергией вращения:
![]() .
.
Если вращение отсутствует (I=0), то ![]() определяется
только размерами Ч.д. При максимально возможной скорости вращения Ч.д. второе слагаемое
под корнем равно первому.
определяется
только размерами Ч.д. При максимально возможной скорости вращения Ч.д. второе слагаемое
под корнем равно первому.
4. Физические процессы в поле тяготения черной дыры
В эргосфере Ч.д. возможны процессы, приводящие к уменьшению энергии вращения Ч.д.,
т.е., как оказывается, Ч.д. может терять энергию. В частности, когда в эргосферу
влетае
частица, имевшая вдали от Ч.д. энергию ![]() (включая энергию
покоя), и распадается на две частицы, то распад может произойти таким образом, что
одна
частица упадет на Ч.д., а другая, сравнительно немного увеличив свою скорость в момент
распада, перейдет на такую орбиту, что вылетит из эргосферы с огромной скоростью.
Эта
скорость может намного превышать и первоначальную скорость подлета частицы к эргосфере,
и величину изменения скорости при распаде. В результате полная энергия вылетевшей
частицы
(включая энергию
покоя), и распадается на две частицы, то распад может произойти таким образом, что
одна
частица упадет на Ч.д., а другая, сравнительно немного увеличив свою скорость в момент
распада, перейдет на такую орбиту, что вылетит из эргосферы с огромной скоростью.
Эта
скорость может намного превышать и первоначальную скорость подлета частицы к эргосфере,
и величину изменения скорости при распаде. В результате полная энергия вылетевшей
частицы
![]() окажется больше
окажется больше ![]() . Избыток энергии
. Избыток энергии
![]() черпается из энергии вращения Ч.д. Энергия
вращения Ч.д. может уменьшаться также при рассеянии эл.-магн. волн на Ч.д. Рассеянная
волна при определенных условиях может оказаться интенсивнее падающей. Потеря энергии
вращения Ч.д. при распаде частицы в эргосфере достигает максимума, когда распад происходит
на горизонте. При этом площадь горизонта не меняется. Во всех других случаях площадь
горизонта несколько увеличивается за счет энергии частицы, упавшей в Ч.д. Оказывается,
что площадь горизонта Ч.д. не уменьшается ни при каких процессах вообще (за исключением
медленного самопроизвольного квантового испарения Ч.д., о к-ром говорится далее).
Напр., ч.д. могут столкнуться и слиться в одну. Часть их энергии будет унесена при
этом за
счет излучения гравитац. волн, но горизонт возникшей Ч.д. будет по площади больше,
чем сумма площадей горизонтов первоначальных дыр. Ни при каких воздействиях (приливных
и
других) Ч.д. не может разделиться на две или большее количество Ч.д.
черпается из энергии вращения Ч.д. Энергия
вращения Ч.д. может уменьшаться также при рассеянии эл.-магн. волн на Ч.д. Рассеянная
волна при определенных условиях может оказаться интенсивнее падающей. Потеря энергии
вращения Ч.д. при распаде частицы в эргосфере достигает максимума, когда распад происходит
на горизонте. При этом площадь горизонта не меняется. Во всех других случаях площадь
горизонта несколько увеличивается за счет энергии частицы, упавшей в Ч.д. Оказывается,
что площадь горизонта Ч.д. не уменьшается ни при каких процессах вообще (за исключением
медленного самопроизвольного квантового испарения Ч.д., о к-ром говорится далее).
Напр., ч.д. могут столкнуться и слиться в одну. Часть их энергии будет унесена при
этом за
счет излучения гравитац. волн, но горизонт возникшей Ч.д. будет по площади больше,
чем сумма площадей горизонтов первоначальных дыр. Ни при каких воздействиях (приливных
и
других) Ч.д. не может разделиться на две или большее количество Ч.д.
В эргосфере Ч.д. могут протекать квантовые процессы рождения частиц. В сильном поле тяготения Ч.д. вакуум (представляет собой физ. поля в наинизшем энергетическом состоянии) не устойчив и из него могут рождаться частицы и античастицы, в основном безмассовые: фотоны, нейтрино, гравитоны.
Рожденные частицы, улетая из эргесферы на бесконечность, уносят энергию Ч.д. Характерная
частота ![]() рождающихся фотонов по порядку величины равна
рождающихся фотонов по порядку величины равна ![]() .
Скорость потери энергии вращения Ч.д. определяется соотношением:
.
Скорость потери энергии вращения Ч.д. определяется соотношением:
![]() .
.
Чрезвычайно важно, что вакуум неустойчив в поле тяготения не только вращающейся Ч.д.,
но и невращающейся. Это означает, что за счет квантовых процессов невращающаяся Ч.д.
также теряет энергию, уменьшаются ее масса и размеры. Невращающаяся Ч.д. излучает
как абсолютно черное тело с темп-рой T=1011(1015/![]() ) К, полная мощность эл.-магн. излучения L=1010(1015/
) К, полная мощность эл.-магн. излучения L=1010(1015/![]() ) эрг/с, а время существенного
уменьшения массы Ч.д.
) эрг/с, а время существенного
уменьшения массы Ч.д. ![]() лет,
где
лет,
где ![]() - значение массы Ч.д. в г. Приведенные соотношения
показыввают,
что квантовые процессы совершенно ничтожны для Ч.д., возникших из звезд с массами
- значение массы Ч.д. в г. Приведенные соотношения
показыввают,
что квантовые процессы совершенно ничтожны для Ч.д., возникших из звезд с массами
![]() >1034 г. Однако они существенны
для
маломассивных первичных Ч.д., к-рые могли возникать на ранних этапах расширения Вселенной.
>1034 г. Однако они существенны
для
маломассивных первичных Ч.д., к-рые могли возникать на ранних этапах расширения Вселенной.
По мере уменьшения массы Ч.д. мощность излучения должна расти, и в конце концов маленькая Ч.д. породит мощную вспышку жесткого гамма-излучения (последние 109 г Ч.д. излучает за 0,1 с, что подобно взрыву миллиона мегатонных водородных бомб).
В реальных условиях Вселенной ч.д., к-рые могли возникнуть из звезд, все время увеличивают свою массу за счет падения на них газа и излучения, в т.ч. и реликтового излучения Вселенной. Увеличение массы Ч.д. при этом хотя обычно и мало, но существенно превышает потери за счет квантового испарения.
Ч.д., возникшие в результате коллапса массивных звезд, могут вызывать своим сильным гравитац. полем бурные процессы при падении в них газа. Такие газовые потоки могут быть особенно мощными, когда на Ч.д., входящую в состав тесной двойной звездной системы, газ перетекает от звезды-гиганта. Газ, нагретый при падении в поле тяготения Ч.д., дает рентг. излучение, и по этому излучению Ч.д. может быть обнаружена. Вероятно, одна ч.д. уже обнаружена таким способом в рентг. источнике Лебедь Х-1 (см. Рентгеновская астрономия, Аккреционные диски).
Возможно, что в центре ядер галактик и квазаров существуют сверхмассивные Ч.д., с
массой до ![]() , в поле тяготения к-рых протекают
бурные
процессы, являющиеся причиной активности ядер галактик и квазаров.
, в поле тяготения к-рых протекают
бурные
процессы, являющиеся причиной активности ядер галактик и квазаров.
Лит.:
Зельдович Я.Б., Новиков И.Д., Теория тяготения и эволюция звезд, М., 1971; Мизнер
Ч., Торн К., Уилер Дж., Гравитация, т. 3, пер. с англ., М., 1977; Фролов В.П., Черные
дыры
и квантовые процессы в них, УФН, 1976, т. 118, в. 3, с. 473; Торн К., Поиски черных
дыр, пер. с англ., там же, с. 453.
(И.Д. Новиков)
|
Публикации с ключевыми словами:
черные дыры - black hole
Публикации со словами: черные дыры - black hole | |
См. также:
Все публикации на ту же тему >> | |