Радиоэхо с длительными задержками: новый подход к проблеме
Радиоэхо с длительными задержками: новый подход к проблеме
Р.Т. Файзуллин
Омский Государственный Университет
(Материалы конференции "SETI-XXI")
Одними из наиболее вероятных кандидатов на роль инопланетного сообщения являются неоднократно фиксировавшиеся с самого начала эры радио, задержки радиосигналов: так называемый "парадокс Штермера", "мировое эхо", "long delayed echoes" (LDE). Имеются в виду радиоэхо с очень длительными задержками и аномально малыми потерями энергии. В отличие от известных эхо с задержками в доли секунды, механизм которых давно объяснен, задержки радиосигналов в секунды, в десятки секунд и даже минуты остаются одной из самых давних и интригующих загадок физики ионосферы [1]. Сейчас трудно себе представить, но в начале века любые зарегистрированные радиошумы первым делом и с легкостью эпохи штурма и натиска, рассматривались как сигналы внеземной цивилизации:
"Отмеченные мной перемены происходили в определенное время, и аналоги между ними и цифрами была настолько четкой, что не мог увязать их ни с одной известной мне причиной. Мне знакомы естественные электрические помехи возникающие из-за солнца, полярного сини и теллурических токов, и я был уверен, как только можно быть уверенным в фактах, что эти помехи не вызваны ни одной из обычных причин... Только через какое-то время меня осенило, что наблюдаемые мною помехи могли возникнуть в результате сознательных действий. Все сильнее охватывает меня предчувствие, что первым услышал приветствие от одной планеты другой... Несмотря на слабость и нечеткость, оно дало мне глубокую убежденность и веру, что вскоре все люди как один устремят на небосвод над нами взгляды, переполненные любовью и почтением, захваченные радостной новостью: Братья! Мы получили сообщение с другой планеты, неизвестной и далекой. И звучало оно: раз... два... три..."
Николай Тесла, 1900
Но с LDE было не так, - идея о том, что радиоэхо может быть искусственным явлением, своеобразной визитной карточкой; внеземного спутника, привлекающего наше внимание, эта идея была выдвинута только после публикации астрономом Рональдом Брейсуэллом краткой заметки напечатанной в журнале Nature, в 1960 году. В начале же, LDE были восприняты как свидетельства наличия в космическом пространстве специфических облаков быстро движущейся плазмы, способных не просто отражать радиосигналы, подобно земной ионосфере, но и фокусировать исходный сигнал так, что мощность отраженного сигнала превышает треть мощности исходного! Исходным моментом послужило письмо инженера Йоргена Халса известному астрофизику Карлу Штермеру
"... At the end of the summer of 1927 I repeatedly heard signals from the Dutch short-wave transmitting station PCJJ at Eindhoven. At the same time as I heard these I also heard echoes. I heard the usual echo which goes round the Earth with an interval of about 1/7th of a second as well as a weaker echo about three seconds after the principal echo had gone. When the principal signal was especially strong, I suppose the amplitude for the last echo three seconds later, lay between 1/10 and 1/20 of the principal signal in strength. From where this echo comes I cannot say for the present, I can only confirm that I really heard it." [2]
Для подтверждения этих фактов астрофизик Штермер, физик Ван-дер-Поль (знаменитое уравнение Ван-дер-Поля) и инженер Халс организовали серию экспериментов, целью которых было: проверить наличие феномена и его частоту проявления.
В 1927 году передатчик, расположенный в Эйндховене начал передавать импульсы, которые регистрировались Халсом в Осло. Первоначально каждый сигнал представлял собой последовательность трех точек Морзе. Эти сигналы Повторялись каждые 5 секунд. В сентябре режим передатчика был изменен: интервалы были увеличены до 20 секунд. Детали эксперимента описаны недостаточно подробно, так как публикация условий эксперимента произошла в трудах конференции и в ограниченном объеме. 11 октября 1928 года, наконец, были зарегистрированы серии радиоэхо, об этом Ван-дер Поль сообщает в своей телеграмме Штермеру и Халсу: "Прошлой ночью наши сигналы сопровождались эхо, время эхо варьировалось между 3 и 15 секундами, половина эхо больше чем 8 секунд!" Халс и Штермер в свою очередь подтвердили получение эти эхо в Осло. Были получены несколько серий эхо. Регистрировавшиеся радиозадержки варьировались от 3 секунд, до 3.5 минут! В ноябре 1929 года эксперимент был завершен.
Были точно зарегистрированные следующие 5 серий радиозадержек [3]:
1) 15,9,4,8,13,8,12,10,9,5,8,7,6
2) 12,14,14,12,8
3) 12,5,8
4) 12,8,5,14,14,15,12,7,5,5,13,8,8,8,13,9,10,7,14,6,9,5,9
5) 8,11,15,8,13,3,8,8,8,12,15,13,8,8 (в секундах)
В мае того же 1929 года Ж. Голль и Г. Талон провели новое успешное исследование LDE феномена:
"... In May 1929, a French expedition was in Indo-China to study an eclipse of the Sun. J B Galle and G Talon, captain of the naval vessel L'Inconstant, had orders to study the effects of the eclipse on radio propagation, particularly long delayed echoes. They used a 500 watt transmitter with a 20 metre aerial attached to an 8 metre mast, powered by the generators of the Indo-China Hydrographic Service vessel La Perouse. The two aptly named ships sailed from Saigon on May 2nd, and on May 5th they conducted test transmissions in "la baie de Penitencier", PouloCondere, and detected long delayed echoes. Weather conditions prevented work on May 6th and 7th, but on the 8th the ships were back on station and transmitted for the first ten minutes of every half hour. On May 9th, the day of the eclipse, signals were sent for nearly six hours with one 20 minute break, and again for ten minutes in every half hour the following day. Two dots were sent every 30 seconds on 25 metres wavelength, varying in a fixed musical sequence to aid correct identification and timing of the echoes. Large numbers of echoes were heard, clearly divided into two groups: weak echoes, about 1/100 the original signal strength, and strong ones 1/3 to 1/5 the intensity of the transmitted signal, with no significant relation between strength and delay time. (These intensities are too great for natural reflection at such apparent distances, but no-one seems to have thought of that at the time.) In their preliminary report Galle and Talon said echoes stopped altogether during the totality of the eclipse, but in fact they paused 3 1/2 minutes before the eclipse became total and began again half way through it. Delay times ranged from 1 second to 30 seconds, though two 31 second echoes and of 32 seconds were heard between 15.40 and 16.00 on the day of the eclipse. 1 and 2 second echoes might seem impossible for a probe in the Moon's orbit, but for an extraordinary circumstance. At 14h 19m 29s on the day of the eclipse the operator "forgot" to send the required dots, but 5 and 10 second echoes were heard nonetheless. From this Galle and Talon concluded that some echoes might have 40 seconds delay or more: either theirmusical tone sequence let them down, or they were unable to believe evidence that the probe was anticipating their signals as it transmitted its "replies" [4, 5, 6].
В 1934 году феномен "задержанного радиоэха" наблюдал англичанин Е.Эпплтон и его данные, оформленные в виде гистограммы, являются одними из наиболее четко оформленных материалов по LDE экспериментам [1] (Рис. 1).
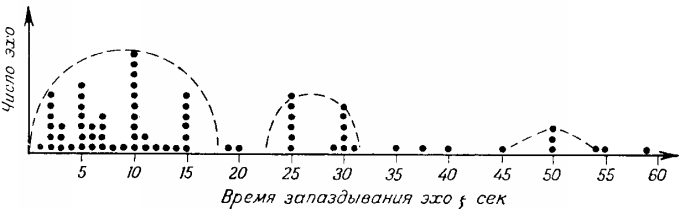
|
|
Рис. 1. |
В 1967 году эксперименты по обнаружению LDE проводились в Стэнфордском университете Ф.Кроуфордом. Феномен удалось подтвердить, но особо длинные радиоэхо и серии, подобные тем, что наблюдались в 20-30-х годах, не были обнаружены. Часто встречались задержки со временами 2 и 8 секунд, со сдвигом частоты и сжатием времени между импульсами эхо по сравнению со времене между импульсами основного сигнала. Опыт исследования известных данных LDE приводит к еще одному любопытному наблюдению - в любом новом диапазоне радиоволн, т.е. в том диапазоне, который только начинает использоваться, феномен проявляется четко и серийно, так же, как и в 20-х годах, затем, по прошествии нескольких лет эхо "расплываются" и перестают фиксироваться серии.
Английский астроном Лунен [6] обратил внимание на то, что эхо, наблюдавшиеся в 20-х годах, были свободны от временного сжатия, и не было доплеровского сдвига частот, и интенсивность штермеровских частот оставалась постоянной, независимо от времени запаздывания. Последний факт очень трудно объяснить, оставаясь в рамках предположений о естественности сигнала - естественные радиоэхо с задержкой 3 секунды и 3 минуты принципиально не могут быть одной интенсивности - происходит рассеивание сигнала, так как волна испускаемая передатчиком это все-таки не когерентный лазерный импульс!
Именно Дункан Лунен выдвинул гипотезу о том, что эхо штермеровских серий представляет собой сигнал межзвездного зонда и изменение времени запаздывания представляет собой попытку передачи какой-то информации. Предполагая, что информация эта о месте нахождении планетной системы, с которой прибыл зонд, он, основываясь на аналогии с картиной созвездий на звездной сфере, пришел к выводу, что родная звезда отправителей зонда - это эпсилон Волопаса:
" ... If the data points are plotted with delay time on the y-axis (normal scientific practice, followed by all the 1920s experimenter' s who presented their results graphically), nothing significant appears. With delay time on the x-axis, however, the graph looks more like an intelligent signal . There is a vertical "barrier" at 8 seconds dividing the diagram into two parts of an equal area; on the left there is a single dot, at three seconds, which was unique in being an exact repeat of the transmitted signal, three dots, the other echoes being 2 second long dashes. On the right of the barrier the main figure has a striking but incomplete resemblance to the constellation Bootes, the Herdsman . If the 3 second dot is transplanted across the barrier to a corresponding position on the right, it occupies the position of the star Epsilon Bootis and so completes the constellation figure. ..."
Им была рассмотрена одна из штермеровских серий 1928 года:
8, 11, 15, 8, 13, 3, 8, 8, 8, 12, 15, 13, 8, 8.
Произвольность геометрических построений Лунена была показана почти сразу же и не скептиками, а самими энтузиастами - болгарские любители астрономии с помощью иного способа дешифровки получили другую "родину" отправителей - звезду дзета Льва, а способ расшифровки А.Шпилевского, наконец, позволил получить и всем известную, так всеми ожидаемую, тау Кита.
Сложившаяся ситуация была очень похожа на ту, которую описал в своем романе "Глас Господа" Станислав Лем - краткая заметка, промелькнувшая в печати и содержащая намек на Контакт была утоплена в море псевдонаучных публикаций, после которых любой серьезный человек не рассматривал весь массив информации без предвзятости. Правда в случае Лунена не понадобилось участие спецслужб, и не понадобилась, дезинформация - все случившееся можно рассматривать, как процедуру верификации, проведенную, как мы уже упоминали, самими энтузиастами ... То, что подобные "картинки" можно продуцировать без особого труда показывает Рис. 3.
На нем изображены координаты импульсов зарегистрированных в эксперименте МЕТА и опубликованные в Астрофизическом журнале [7]. Каждый из этих импульсов был подобен широко известному "сигналу" Wow! и они были зарегистрированы на той самой "горячей" линии ? волне длиной 21 см! Что же мы видим, если соединить небесные координаты сигналов по порядку определяемому датами, то мы получим "траекторию" некоего космического корабля, который подобно самолету, время от времени мигал нам сигнальными огнями (Рис. 3).
|
|
|
Рис. 2. |
Казалось бы все - вот они! Но, к сожалению, это всего лишь артефакт - устройство, с помощью которого сканировалось небо, сканировало лишь очень маленький интервал по вертикали, и день ото дня интервал этот поднимался вверх, а затем, достигнув максимальной вертикальной отметки, начал опускаться вниз. Уже следующий рисунок, на котором таким же образом упорядочены "сигналы" на удвоенной длине волны 42 см, показывает, что "траектория" получилась чисто случайно (Рис. 4).
В чем же заключалась ошибка Лунена? Если задана произвольная конфигурация точек, мы почти всегда можем найти подходящую конфигурацию на звездном небе. Это утверждение есть не что иное, как частный случай так называемой теоремы Рамсея - то есть при достаточном количестве точек или объектов мы можем найти среди этих точек заранее заданную конфигурацию с заранее определенными свойствами. Идеально точно она, конечно, не получится, но, увеличивая мощность рассматриваемого множества точек (т.е. числа точек или звезд на звездной сфере) мы можем получить сколь угодно точную копию заданной фигуры.
|
|
|
Рис. 3. |
|
|
|
Рис. 4. |
То есть ошибка Лунена состояла в том, что он пытался построить фигуру, используя задержки, которая бы выглядела КАК созвездие. Но созвездий много, да они и сами являются культурными артефактами - способ группировки звезд по созвездиям произволен и те, определенные созвездия, что у нас есть сейчас, это всего лишь плод художественного воображения вавилонских и греческих пастухов и не более того.
Прежде чем переходить к гипотезе являющейся предметом данной статьи рассмотрим некоторые естественные ограничения, и очевидные требования, которым должно удовлетворять возможное контактное сообщение.
Следует ожидать, что процедура передачи, как и само содержание, сообщение, представляет собой некий очень хорошо продуманный и неоднократно приводивший к успеху стандарт. Поэтому само сообщение должно рассматриваться как продукт высочайших технологий, продукт, прошедший испытания не один десяток раз и вероятней всего разработанный даже не той цивилизацией, что посылает сообщение в данный момент времени. Следует подчеркнуть, что речь идет не только о технологиях в обычном смысле этого слова, но и о социальных технологиях.
Какие отсюда следуют выводы? Во-первых, следует ожидать гарантированность успеха распознавания искусственности сообщения. Это означает, что с высокой вероятностью фиксация сообщения влечет за собой и его распознавание. Отсюда очевидным образом следует, что сообщение должно быть обязательно зафиксировано, то есть, занесено в анналы науки, религии или других долговременных организаций. Одномоментности расшифровки, или вернее одномоментности осознания ожидать не следует, во всяком случае, она очень маловероятна.
Следующее - должно ли быть сообщение избыточным? Это довольно тонкий вопрос, что именно понимать под избыточностью, и так ли она полезна. Рассмотрим пример связанный с знаменитым сигналом "Ого-го!" или "Wow!". Пусть из той же точки небесной сферы, где первоначально был получен этот странный сигнал, будут поступать его аналоги, причем временные интервалы между их поступлениями будут относиться между собой как простые числа (так называемые позывные). Будет ли это свидетельством искусственности? Несомненно. Но, есть многое зависящее и от получателя. Будет ли получатель сканировать на протяжении долгого времени (столетий) именно этот участок неба, дело не в угасающем научном интересе, дело в рутинных финансовых возможностях?
Будет ли небо получателя чисто от подобных радиосигналов (спутники)? Кроме того, кто гарантирует, что в природе нет физических процессов, при которых происходят спонтанные разряды с интервалами времени, относящимися друг к другу, как простые числа? Таким образом, избыточность "сигнала" наоборот может служить основанием для принятия решения об его естественном происхождении.
(Последние исследования о спонтанных сцинтилляциях в межзвездных облаках водорода ставят под сомнение саму возможность подобного канала связи, т.к. естественные сцинтилляции создают шум, причем шум, который в силу своей сложности может походить на искусственный сигнал, т.е. опять проявляется теория Рамсея).
Вместо избыточности следует ожидать независимости. Мы постепенно перешли к обсуждению возможного содержания сигнала или как принято называть - позывных. Примеры позывных уже есть, хотя это и примеры земного происхождения (Пионеры 10, 11 и последующие, дальние зонды Вояджеры), и на основании реальных сообщений можно вполне обоснованно сделать предположения о первоначальной (в историческом плане) форме стандартного сообщения - немного о себе, координаты, и что-нибудь о Космосе.
Изменится ли что-нибудь потом?
"Когда человек узнает, что движет звездами, тогда Сфинкс засмеется, и род людской прервется" (Надпись на стенах Абу Симбела)
Сколько бы времени ни прошло, как бы не различались уровни развития цивилизаций, но контактное сообщение всегда будет направлено тем, кого интересуют звезды. Это должно быть то, что отличает человека от животного, даже от разумного животного.
Следующий немаловажный момент, опять приводящий нас к звездам - это интервал времени, в котором контактное сообщение будет представлять интерес для получателя. В нашем случае этот интервал условно можно взять равным всему времени существования человека как вида, т.е. это примерное 100 000 лет!
Можно, конечно, заявить, что все основные факты о звездах мы уже знаем, но такое утверждение само далеко не ново ...
Все вышесказанное позволяет выдвинуть следующую гипотезу и сформулировать требования к ее верификации:
- Времена задержек сигнала следует интерпретировать как номера небесных тел в некотором объективном упорядочении.
- Следует искать неожиданные геометрические свойства, присущие фигурам, полученным на звездной сфере и в случае успеха попытаться установить математический и физический смысл данных свойств.
- Полученные факты должны подтверждаться для нескольких независимых серий радиозадержек, полученных в разное время и разными исследователями, что позволит исключить произвольность интерпретации и "подделку" данных.
- Полученные результаты должны пройти стандартную научную апробацию в виде выступлений на научных конференциях и в виде опубликованных научных статей (без упоминаний или ссылок на проблему SETI), что должно подтвердить независимую от гипотезы Контакта значимость выявленных математических и физических фактов.
Прежде чем переходить к конкретным результатам, обсудим более детально представленные пункты. Рассмотрим пункт 1, и выясним, какие небесные тела имеются в виду. Планеты? Но часть из них не может быть наблюдаема невооруженным глазом и требование к "демократичности", т.е. требование к тому, что полученное знание было бы визуальным и доступным максимальному количеству наблюдателей в случае планет не выполняется. Ближайшие к нам звезды? Но аналогично планетам самые близкие к нам звезды могут быть и не видны без телескопа, настолько они малы по массе и светимости. Кроме того, скорости малых звезд настолько велики, что их позиции на звездной сфере за тысячи лет изменяются очень сильно и предполагаемая фигура "расплывается". То же относится к галактикам, ярким туманностям и прочим слабосветящимся объектам. Остаются наиболее яркие звезды, относительные скорости их малы, они наблюдаемы, они всегда вызывали интерес.
По каким параметрам их можно упорядочить? По расстояниям, по массам, по светимостям?
Но их параллаксы даже сейчас определены не совсем точно, массы являются вторичными расчетными величинами, и остаются светимости или более точно визуальные звездные величины V.
Эти величины определяются с высокой точностью фотоэлектрическим методом, и одновременно их можно определить с помощью экспертной оценки на самой ранней стадии цивилизации.
Ниже приведены координаты и названия первых пятидесяти по визуальной яркости звезд.
Упорядочение наиболее ярких звезд по величине V.
(Куликовский [8], 1985)
| l | b | |||
| 1. Сириус | 6h 43m | -16 35 | 227 | -9 |
| 2. Канопус | 6h 23m | -52 40 | 261 | -25 |
| 3. Арктур | 14h 13m | +19 27 | 15 | +69 |
| 4. Вега | 18h 35m | +38 44 | 67 | +19 |
| 5. Толиман | 14h 36m | -60 38 | 316 | +1 |
| 6. Капелла | 5h 13m | +45 57 | 163 | +5 |
| 7. Ригель | 5h 12m | -08 15 | 209 | -25 |
| 8. Процион | 7h 37m | +05 21 | 219 | +13 |
| 9. Бетельгейзе | 5 52 | +07 24 | 200 | -9 |
| 10. Ахернар | 1 36 | -57 29 | 291 | -59 |
| 11. Хадар | 14 00 | -60 08 | 314 | .0 |
| 12. Альтаир | 19 48 | +08 44 | 48 | -9 |
| 13. Акрукс | 12 24 | -62 49 | 300 | 0 |
| 14 Альдебаран | 4 33 | +16 25 | 181 | -20 |
| 15. Антарес | 16 26 | -26 19 | 352 | +15 |
| 16. Спика | 13 23 | -10 54 | 316 | +51 |
| 17. Поллукс | 7 42 | +28 09 | 192 | +23 |
| 18. Фомальгаут | 22 55 | -29 53 | 20 | -65 |
| 19. Мимоза | 12 45 | -59 09 | 302 | +3 |
| 20. Денеб | 20 40 | +45 06 | 84 | +2 |
| 21. Регул | 10 06 | +12 13 | ||
| 22. Адара | 6 57 | -28 54 | ||
| 23. Кастор | 7 31 | +32 00 | ||
| 24. Шаула | 17 30 | -37 04 | ||
| 25. Беллатрикс | 5 22 | +06 18 | ||
| 26. Гакрукс | 12 28 | -56 50 | ||
| 27. Эль-Нат | 5 23 | +28 34 | ||
| 28. Миаплацидус | 9 13 | -69 31 | ||
| 29. Алнилам | 5 34 | -01 14 | ||
| 30. Аль Наир | 22 05 | -47 12 | ||
| 31. Алиот | 12 52 | +56 14 | ||
| 32. Алнитак | 5 38 | -01 58 | ||
| 33. Дубхе | 11 01 | +62 01 | ||
| 34. Мирфак | 3 21 | +49 41 | ||
| 35. Гамма Пар | 8 08 | -47 12 | ||
| 36. Каус Ауст | 18 21 | -34 25 | ||
| 37. Везен | 7 06 | -26 19 | ||
| 38. Бенетнаш | 13 46 | +49 34 | ||
| 39. Авиор | 8 22 | -59 21 | ||
| 40. Тэта Ск | 17 34 | -42 58 | ||
| 41. Менкалинан | 5 56 | +44 57 | ||
| 42. Альхена | 6 35 | +16 27 | ||
| 43. Металах | 16 43 | -68 56 | ||
| 44. Дельта Пар | 8 43 | -54 31 | ||
| 45. Пикок | 20 22 | -56 54 | ||
| 46. Мирзам | 6 20 | -17 56 | ||
| 47. Альфард | 9 25 | -08 26 | ||
| 48. Мира | 2 17 | -03 12 | ||
| 49. Хамаль | 2 04 | +23 14 | ||
| 50. Полярная | 1 49 | +89 02 |
(Гиппарх первый упорядочил звезды по звездной величине собрав несколько человек, славившихся исключительно острым зрением, он предложил им оценить по порядку яркости звезды. Усреднив результаты, он получил свою шкалу. Это было не что иное, как первое научное применение так называемого метода экспертной оценки. Заметим, что упорядочение Гиппарха несколько отличается от упорядочения по фотоэлектрической величине)
Второй пункт, какие фигуры следует искать? Опыт неудачи Лунена демонстрирует, что поиск антропоморфных символов, скорее всего обречен на неудачу и поиск следует направить на математические фигуры, не случайные по своей сути и являющиеся отражением законов звездной динамики. Но какое отношение имеет звездная величина к динамике? Известно, что полная светимость звезды L является функцией от ее массы, более точно она пропорциональна массе в кубе, плюс некая мала величина, а визуальна звездная величина, очевидно пропорциональна L/R2. То есть, звездная величина является автомодельным параметром, одновременно характеризующим и массу и расстояние.
Третий пункт есть не что иное, как обычное требование к эксперименту - повторяемость исключает случайность. То же относится и к четвертому пункту, можно представить себе, что случайным образом мы получили нечто странное и "похожее" на математическую фигуру, но сам факт публикации служит доказательством значимости результата. Публикации предполагают не только описание феномена, но и некоторое развитие, например, подтверждение предложенной физической модели численными экспериментами, создание новых алгоритмов, на основе наблюдаемых феноменов и т.п. Также - какова вероятность того, что, основываясь на случайном наборе чисел можно получить научный факт?
Перейдем к непосредственному рассмотрению фактов и выдвижению гипотезы.
Рассмотрим так называемую первую серию Штермера:
15, 9, 4, 8, 13, 8, 12, 10, 9, 5, 8, 7, 6.
Естественно ожидать, что эта серия, если, конечно, она является искусственным посланием, содержит "позывные" - некоторый геометрический факт, иллюстрацию, подобную той, что была предложена Гауссом (теорема Пифагора иллюстрированная вырубками в сибирских лесах или каналами с горящей нефтью в Сахаре).
Что особенного в представлении этих звезд? Если рассматривать их в обычных декартовых координатах в пространстве или на звездной сфере, то казалось бы ничего необычного нет, но давайте перейдем в сферическую систему координат.
Как она строится? Рассмотрим звездную сферу с радиусом единица, то есть представим, что мы как наблюдатели находимся на Земле, а нас окружает очень большая сфера. Пусть звезды, находящиеся снаружи сферы, проектируются на эту сферу и мы, пренебрегая расстояниями до них, видим только яркие точки на сфере. Каждая такая точка лежит на пересечении линии со сферой, линии проведенной через центр сферы и реальным местоположением звезды. Тогда звезде можно сопоставить угловые координаты (l,b).
Через центр сферы проходит плоскость, выбрав некий луч на этой плоскости, проходящий через центр, можно отсчитывать угол относительно луча- это одна координата l. Друга получается как угол b между плоскостью и лучом, направленным из центра сферы на точку сферы, которая не лежит на данной плоскости.
Очевидно, что угол l меняется от нуля до 360 градусов, а b варьируется от -90 до +90 градусов. Тогда если рассмотреть систему координат, где в качестве оси OX выступает OL, а в качестве оси OY ось OB, то мы получим представление всех звезд в прямоугольнике [0,360]x[-90,90]. Казалось бы, разница заключается лишь в удобстве представления данных, но не все так просто. Например, в качестве секущей звездную сферу плоскости можно выбрать произвольную плоскость, но можно выбрать и плоскость вращения системы наблюдателя! Т.е. выбрать динамически выделенную систему координат связанную с моментом вращения. Так под (l,b) понимается галактическая система координат, где плоскость сечения звездной сферы совпадает с плоскостью Галактики, l = 0 выбрано, конечно, произвольно, но может быть и не совсем произвольно, так как l = 0 отвечает направлению на центр Галактики.
Другая система координат соотнесена с плоскость эклиптики и отвечает плоскости вращения или соответствует моменту Солнечной системы и третья сферическая система координат, это экваториальная, здесь секущая плоскость перпендикулярна оси вращения Земли.
Отметим, что в силу произвольности выбора начала l = 0 и периодичности, мы имеем для представления звезд не прямоугольник, а цилиндр, восстановленные перпендикуляры над l = 0 и l = 360 задают одни и те же прямые.
На первый взгляд, данная система координат кажется надуманной и неудобной, но на самом деле неудобно именно декартово представление, сферические же системы координат, позволяют изображать всю звездную сферу на ограниченном куске плоскости и являются естественными, в силу локальной сферической симметрии, в силу изотропности пространства, и в силу естественной связи l-координаты с моментом вращения системы.
Тогда в галактической системе координат мы получаем действительно удивительную фигуру, фигуру, которая вполне может выполнять роль "позывных" (Рис. 5).
Мы получили 8 прямых из которых, следуя порядку поступления сигналов можно образовать две тройки параллельных прямых и еще одну пару взаимно параллельных (Рис. 6, Рис. 7).
Отметим, что произвольная выборка из номеров, отвечающих первой серии Штермера, уже не дает подобной симметрии и более того, вероятность случайной и настолько полной иллюстрации свойства параллельности, при случайном обходе заданных точек, равна числу порядка 1/(12!). ( Код, если это код, легко поддается расшифровке - соединяя первые 5 точек в порядке 15, 9, 4, 8, 13 мы получаем две параллельные прямые и далее становится совершенно очевидным, что необходимо провести прямые 13, 8, 12, чтобы получить отрезки (8, 12), (12, 10) и.т.д., здесь, наверное, стоит вспомнить идею о кодах максимально простых для расшифровки и о уже существующих кодах с исправлением ошибок).
|
|
|
Рис. 5. |
|
|
|
Рис. 6. |

|
|
Рис. 7. |
Оказывается, что и четвертая серия Штермера является иллюстрацией свойства параллельности. Например, обход точки на плоскости (l,b), в порядке 12 8 5 14 14 15 12 7 5 5 13 8 8 8 13 9 10 7 14 6 9 5 9 мы получаем аналогичную фигуру (Рис. 8). Свойство параллельности проиллюстрировано на следующих рисунках 9-12
Заметим, что здесь мы заменили 11 по счету отметку (или 11-й эхо-сигнал) равную 13 на 14, принципиально это не меняет картину, но добавляет пару "параллельных" прямых.
Возможно, при регистрации радиоэха была допущена ошибка, но как мы видим, она не влияет на дешифровку в целом! Далее, эти большие по объему серии, будем считать "оберткой" письма выполняющие одновременно функцию "содержания" и попытаемся найти некоторое объективное объяснение тому, что для казалось бы совершенно случайно распределенных точек на плоскости удается построить столько почти параллельных прямых. Непосредственная проверка показывает, что если взять, к примеру, координаты ближайших 50 звезд, то подобной богатой "параллельности" не наблюдается, также ее не наблюдается в случае если мы рассматриваем случайные наборы точек.
|
|
|
Рис. 8. |
|
|
|
Рис. 9. |
|
|
|
Рис. 10. |
|
|
|
Рис. 11. |
|
|
|
Рис. 12. |
Будем далее считать, что галактическая система координат это то поле или "доска", на которой в дальнейшем будет представлена информация и рассмотрим 3 серию зарегистрированную Штермером, Халсом и Ван-дер-Полем - задержки равные 12,5, 8.
Снова рассматривая упорядочение по звездным величинам, измеренным фотоэлектрическим способом (данные взяты из монографии Куликовского), мы получим следующие, соответствующие номерам звезды, 5- альфа Центавра (арабы называют ее Толиман), 8 - Процион, 12 - Альтаир. Оказывается, что эти три звезды лежат на одной линии, причем точка 5 лежит на "перекрестье" двух линий (если рассматривать цилиндр). Обратимся ко второй серии Штермера 12, 14, 14, 12, 8, здесь к указанным трем звездам добавляется Альдебаран.
Опять три звезды 14, 12, 8 лежат примерно на одной линии, которая, кстати, содержит и точку 5. Пойдем дальше и сделаем допущение, что значимы не только сами задержки - эхо, но и их дополнения до 20, мы учитываем конкретные условия эксперимента Штермера и, считая, что сигналы имеют искусственный характер, мы можем рассматривать как равноправные данные и задержки и их дополнения (Рис. 13).
Добавляются всего две новых звезды 6 - Капелла и 15 - Антарес, но картина приобретает завершенный и исключительно симметричный вид. Может быть это случайное совпадение? Пусть даже и переход в другие сферические системы координат, в эклиптическую (Рис. 14), и в экваториальную (Рис. 15), сохраняет симметрию, но все-таки может быть отличие от идеальных прямых делает подобные свойства очень вероятными?
Обратим внимание на то, что число 20, или, иначе говоря, интервал между сигналами посланными с Земли, "завязано" в представленных картинах
|
|
|
Рис. 13. |
Например, в галактическом представлении точки с номерами 5 и 6 лежат на перекрестии линий, соединяющих точки с номерами в сумме дающими число 20. В экваториальной же системе координат линии, пересекающиеся накрест, ограничиваются точками, номера, которых взаимно дополнительны до 20. Если рассматривать дополнения до 20, для первой серии Штермера, то мы опять получим иллюстрацию параллельности, т.е. если соединить точки с номерами 5 11 16 12 7 12 8 10 11 15 12 13 14, являющимися дополнительными к номерам 15 9 4 8 13 8 12 10 9 5 8 7 6, то полученный "негатив" просто поражает своей симметрией! (Рис. 16) и опять мы получаем иллюстрацию свойства параллельности.
Проведенные численные эксперименты показывают, что подобные симметрии получить довольно трудно, но более всего доказательно рассмотрение независимых данных - обработка результатов эксперимента Эпплтона 1934 года.
Оказывается, что уже для 50 точек ( позиций 50 звезд) мы можем выделить инвариантную конфигурацию "сетка": в экваториальном (Рис. 17) представлении, в эклиптическом (Рис. 18) и в галактическом (Рис. 19). Здесь также, каждой задержке отвечает звезда, с соответствующим номером и проверяется свойства "лежать на одной прямой". Обратим внимание на то, что "сетка" строится с помощью двух образующих цилиндра.
|
|
|
Рис. 14. |
|
|
|
Рис. 15. |
|
|
|
Рис. 16. |
Легко проверить инвариантность и по пространству, то есть то, что Солнечная система не есть некоторая выделенная система координат. Например, если в качестве начала координат рассматривать местоположение звезды альфа Центавра и пересчитать визуальные яркости 50 звезд, самых ярких в новой системе отсчета (например, минус альфа Центавра, плюс Солнце и некоторые другие звезды), то мы получим полный аналог уже имеющимся картинам (Рис. 20).
То же самое получается в случае переноса начал координат на место Проциона (Рис. 21).
В качестве системы координат выбрана галактическая система, и мы здесь ограничились представлением для двух ближайших соседей Солнца- расстояние до альфы Центавра 4 световых года, а до Проциона 11 световых лет.
Переход к более удаленным звездам, например, к Альтаиру (Рис. 22) также возможен, но требуется очень аккуратный пересчет параллаксов и визуальных яркостей для более чем ста ближайших звезд.
|
|
|
Рис. 17. |
|
|
|
Рис. 18. |
|
|
|
Рис. 19. |
Но что это означает? Какой смысл (пока еще динамический, конечно) кроется за найденными фигурами?
Во-первых, что мы можем сказать о рисунках более точным языком - языком математики? Что можно найти похожего в арсенале геометрии?
Оказывается, есть математические объекты в некотором роде "похожие" на выявленные геометрические природные соотношения. Это так называемые конфигурации [9], простейшим примером может служить конфигурация Брианшона - Паскаля (Рис. 23).
Данные 9 точек удовлетворяют следующим условиям: через каждую точку проходит по три прямые, на каждой прямой лежит по три точки. Поэтому формальное обозначение этого объекта (9)_3
Заметим, что совпадение свойств или "похожесть" проявляется при подобных операциях построения, конфигурации это математические объекты, базовые для проективной геометрии
|
|
|
Рис. 20. |
|
|
|
Рис. 21. |
|
|
|
Рис. 22. |
Для того чтобы исключить элемент случайности обратимся к представлениям ближайших гигантских и сверхгигантских галактик, наиболее ярким галактикам.
Мы рассматриваем галактики сравнимые по массе, например, туманность Андромеды, наша Галактика, Двингело 1, Треугольник - это гигантские галактики, а карликовые галактики по массе в тысячи и десятки тысяч раз меньше гигантских.
При построении аналогичном тому, какое мы проводили для случая ярчайших звезд в экваториальной системе координат мы получим аналог конфигурации Паскаля (Рис. 24). Отметим только, что упорядоченность по яркости здесь не представлена.
Точно также как и в случае ближайших звезд, упорядоченность имеется и в других системах координат эклиптической (Рис. 25), галактической (Рис. 26) и добавляется представление в так называемой cупергалактической (Рис. 27) системе координат, координаты галактик взяты из базы данных внегалактических объектов NED: http://nedwww.ipac.caltech.edu/index.html
|
|
|
Рис. 23. |
|
|
|
Рис. 24. |
|
|
|
Рис. 25. |
Выполнение свойств, выявленных сначала для расположения звезд, и для галактик несколько проясняет ситуацию. Галактики практически покоятся относительно друг друга, - скорости их пренебрежимо малы по сравнению с характерными линейными размерами галактик и расстояниями между ними, то есть полная энергия системы почти совпадает с потенциальной энергией. Но это означает, что потенциальная энергия система достигает своего максимального значения.
Может быть, конфигурационные свойства и есть следствие экстремальности состояния системы?
Что тогда можно сказать относительно системы ближайших ярких и массивных звезд? Ближайшее окружение Солнца находится в так называемом коротационном узле [14], где скорость вращения Галактики и скорость вращения спиральных ветвей совпадают. Это означает, что уже несколько миллиардов лет окружение Солнца движется вне зон, где происходят нестационарные процессы и поэтому можно ожидать, что за это время произошло стационирование распределения масс, связанных сейчас в звезды большой светимости и массы.
Это приводит нас к рассмотрению известной математической проблемы, носящей название задачи Штейнера:
- заданы N точек или на плоскости или в пространстве, необходимо соединить их отрезками прямых так, что сумма длин этих отрезков будет минимальна. Следует учесть, что можно вводить дополнительные точки, кроме тех которые имеются.
|
|
|
Рис. 26. |
|
|
|
Рис. 27. |
В общей, математической постановке задача была сформулирована в статье Милоша Кесслера и Войцеха Ярника опубликованной в 1934 году, но известность к задаче пришла после знаменитой книги Куранта и Роббинса "Что такое математика?" [11]. Курант и Роббинс указали на связь общей постановки задачи с проблемой Штейнера - поиску одной точки, сумма расстояний, от которой до всех точек заданного множества была бы минимальна (Яков Штейнер крупный немецкий геометр 19 века). Дальнейшие следы уводят в глубь веков, еще Эванджелиста Торричелли и Бонавентура Кавальери занимались интересным частным случаем задачи: найти точку Р, сумма расстояний от которой до каждой из трех заданных минимальна. Они доказали, что сумма расстояний минимальна, когда все сопряженные углы больше или равны 120 градусам. Кроме того, они предложили и алгоритм решения задачи.
Чтобы проиллюстрировать сказанное выше приведем геометрические фигуры являющиеся решениями задачи Штейнера (деревья Штейнера) для малого числа точек. Для случая трех точек, расположенных в вершинах правильного треугольника: решение и приближения приведены на рисунке 28.
|
|
|
Рис. 28. |
Для случая 4 точек, расположенных в вершинах прямоугольника, решение и сравнения приведены на следующем рисунке 29.
|
|
|
Рис. 29. |
Нас больше интересуют механические аналогии, когда минимум длины интерпретируется как некий экстремальный энергетический принцип для механической системы. Например, Курант и Роббинс (КР) [11] указали, что если вершины дерева Штейнера рассматривать как соединенные упругой нитью узлы, то минимум длины отвечает минимуму суммарной потенциальной энергии натяжения.
Следуя данной аналогии, они построили остроумное устройство позволяющее находить приближенные решения задачи. КР использовали в качестве модели мыльную пленку, натянутую между двумя параллельными стеклами, соединенными между собой стержнями в положениях заданных точек. Приподнимая одно стекло над другим, КР получали некоторую пленку, соединяющую стрежни. В силу экстремального энергетического принципа положение пленки давало одно из решений задачи. К сожалению, получить точное решение таким способом не всегда представляется возможным, и мы получаем так называемые относительно минимальные деревья Штейнера. Но оказывается, то такие деревья можно получать не только с помощью механического устройства КР.
Обратим внимание на тот факт, что в дереве Штейнера нет вершины, имеющей более трех ребер и кроме того, каждая точка Штейнера, т.е. дополнительная к заданным точка имеет сходящиеся к ней ребра, под углами 120 градусов. Представим себе, что заданные точки дерева фиксированы, а точки Штейнера "ищут" положение статического равновесия, так, чтобы итоговая конфигурация удовлетворяла принципу максимума потенциальной гравитационной энергии (массы точек считаются равными, а потенциальна гравитационная энергия отрицательна).
Тогда можно легко показать, что любое малое отклонение от подобной конфигурации приводит к тому, что суммарная длина ребер дерева Штейнера возрастает и более того, можно ранжировать относительно минимальные деревья Штейнера по "силе" отвечающей заданному возмущению.
Но вместо того, чтобы рассчитывать гравитационные силы, можно рассчитывать вторые производные от координат, и выбирая в итерационной процедуре для каждой точки Штейнера положение с минимальной суммой вторых производных, а проще говоря, ставя ее в центр координат трех ближайших соседей, мы довольно быстро получим приближенное решение задачи. Например, все ранее рассмотренные случаи, получаются после нескольких (4 - 10) итерационных обходов подвижных точек. Очевидно, что трехмерный случай (как и случаи более высокой размерности) ничем не отличается от двумерного. Варьируя начальные приближения, мы получим несколько относительно минимальных деревьев, и если каждое из них получается не один раз, то вероятность того, что мы пропустили самое минимальное, очень мала. Подобным образом удается получить и другие известные точные решения задачи Штейнера (рис 30)
|
|
|
Рис. 30. Точное решение задачи Штейнера, полученное методом гравитационной аналогии (черные кружки - точки Штейнера). |
Вернемся к звездам. Пусть в качестве "заданных" или фиксированных точек дерева Штейнера выступают очень массивные звезды, а в качестве добавочных, или точек Штейнера фигурируют звезды, масса которых несколько меньше. Тогда положение с максимальной потенциальной энергией будет отличаться тем, что звезды средней массы или "точки Штейнера" расположатся так, что каждая будет лежать в плоскости трех своих ближайших соседей.
Что отсюда следует? В сферической системе координат, с плоскостью одного угла l, совпадающей с плоскостью образованной трем соседями, все три звезды-соседки будут лежать на линии l = 0. Если же мы начнем поворачивать плоскость так, что одна звезда будет оставаться в плоскости угла l, то в силу симметрии, в новой сферической системе координат изображение всех трех звезд будет лежать на одной линии, вернее на двух образующих цилиндра, также как и в наблюдаемых случаях.
Можно ослабить условие неподвижности самых массивных звезд и считать фиксированными положения только звезд, лежащих на границе некоторого объема. Оказывается, что и в этом случае симметрии в сферических системах координат сохраняются.
На следующем рисунке 30 приведен пример, когда одна точка уравновешивается тремя.
|
|
|
Рис. 31. |
На рисунке 31 приведен пример, когда рассматриваются уже 5 точек, одна из которых есть точка обзора.
На рисунке 32 приведены результаты расчета для большего числа точек.
Как мы видим, рисунки, полученные в результате моделирования очень похожи на те конфигурации, которые наблюдаются на звездном небе.
|
|
|
Рис. 32. |
|
|
|
Рис. 33. |
Апробация представленных выше материалов, в которых, конечно, ни словом не упоминались, ни проблема SETI, ни феномен LDE, заключалась не только в публикациях статей и в выступлениях на научных конференциях, но и в некотором тесте на значимость результатов, т.е. в наблюдении за реакцией слушателей, и за их оценками уровня новизны представленных геометрических фактов. В большей мере, чем сам факт публикаций, это влило на оценку значимости полученных фактов самим автором.
Т.е это был растянутый по времени социально-психологический эксперимент с обратной связью.
Хронологически первым было выступление на Международной конференции "Группы в геометрии и анализе" Омск 1995. Отметим, что Оргкомитет возглавлял академик Решетняк Ю.Г. и д. ф.-м. н. Винберг Э.Б., то есть конференция по уровню действительно была значимой.
Был представлен доклад с названием "Симметрии в расположении ярких звезд и задача N-тел с конечной скоростью передачи сигнала". Выступление было принято в штыки и вызвало довольно горячую дискуссию, в которой участвовали профессор Винберг и профессор Водопьянов и другие. Но так как автор не претендовал на выдвижение "теорий", а просто представил легко проверяемый экспериментальный факт инвариантности конфигурационных свойств для естественных объектов, то факт был принят во внимание (был принят, надо сказать, скрепя сердце).
Следующим шагом апробации стала дискуссия с академиком А.Т. Фоменко, в августе 1996 года. Его резюме былов следующим:
"Представленные факты, несомненно таят некоторый глобальный по значимости закон, но на данный момент я не вижу математических инструментов способных описать его, может быть стоит обратить внимание на поиск групп, отвечающих данным симметриям, и попытаться промоделировать подобные структуры в ряде численных экспериментов"
В том же 1996 году был сделан доклад "An Approximations for Genetic Algorithms and Star Patterns" [12].
В этой работе, на основе указанных симметрий, был предложен алгоритм оптимизации, где значение целевой функции рассматривалось, как гравитирующая масса, зависящая от местоположения пробной точки, а поиск экстремума функции моделировался, как физический процесс коллапса нескольких таких точек (в дальнейшем разработанный метод гравитационной аналогии был успешно применен в задаче поиска траекторий элементарных частиц в экспериментах физики высоких энергий и в чисто технической задаче оптимизации работы гидравлического устройства.)
С другой стороны, попытки моделирования конфигураций привели к построению приближенного алгоритма решения задачи Штейнера, подобного алгоритму Куранта - Роббинса, пригодному уже не только для плоскости, но и для пространства произвольной размерности.
В 1997 году автором был представлен доклад на XIV Сессии Международной Школы по моделям механики сплошной среды . "Конечноэлементные аналогии при моделировании нестандартных сплошных сред" [13].
Уточненный и расширенный вариант этого доклада был представлен на 2-й Зимней школе по Новым Математическим Методам в Механике, г. Новосибирск, Институт Гидродинамики им М.А.Лаврентьева, 1998 год.
Тезисы докладов были опубликованы также на нескольких научных физических и астрономических конференциях, например, на конференции Вычислительная Астрофизика- 98, Япония, Токио, 2-ой Конгресс по Индустриальной Математике г. Новосибирск, и.т.д.
Следует сделать вывод о том, что в целом реакция слушателей была благожелательной, так, например, иногда даже встречались выкрики "это открытие!" и не было откровенного скепсиса и неприятия, но утверждать, что новые факты стали хорошо известны и интересны широкому кругу исследователей пока нельзя, но этого на первых порах и не требуется.
Остается важный вопрос, можно ли получить, хотя бы предположительную, но все-таки информацию о местонахождении планеты или базы отправителей зонда? Конечно, здесь мы ступаем на зыбкую почву интерпретации символов, но некоторый вывод сделать можно.
Обратим внимание на то, что большая часть задержек зарегистрированных радиоэхо и в 20-ые годы и в экспериментах Кроуфорда равнялась восьми. Числу восемь у нас отвечает звезда Процион, двойная звезда, одна компонента которой белый карлик, а друга это звезда спектрального класса F5 IV, у которой с большой вероятностью нет планет пригодных для жизни. Но почему мы считаем, что сигнал должен указывать непременно на родную планету отправителей? С точки зрения гипотезы о том, что развитая цивилизация уже давно не зависит от ресурсов только материнской планеты, эта звезда одна из наиболее подходящих звезд из ближайшего окружения Солнца, - как временная база, здесь возможно расположить долговременный спутник около высокоэнергетичного белого карлика и орбита спутника будет стабильна.
Конечно, необходимы независимые улики, указывающие на Процион. Оказывается, что они имеются. Рассмотрим пятую серию Штермера, ту самую, на основании которой Лунен сделал вывод о местоположении отправителей, и покажем, что эта серия может содержать информацию о местоположении.
Рассматривая рисунки полученные проведением линий, соединяющих точки с координатами отвечающим номерам звезд, мы получим треугольники (довольно интересные и не случайные треугольники) с общей вершиной в точке отвечающей расположению Проциона.
Если же рассмотреть другое упорядочение звезд по блеску, например, взяв за основу порядок предложенный Гиппархом (или порядок определяемый не фотоэлектрическим, а фотографическим способом фиксации визуальной яркости), то тогда проекции линий соединяющих координаты звезд на плоскость земного экватора будут давать в некотором роде "стрелу", проходящую через центр окружности, и сохраняющую свою форму при переходе к эклиптическим координатам и указывающую на Процион (Рис. 33).
|
|
|
Рис. 34. |
Следует отметить, что здесь, казалось бы, мы отступаем от постулированного ранее требования "объективности" символа, но так ли уж символ "стрела" антропоморфен? Возможно, что символ вектора или направленности также общепринят, как и строго определяемые математические фигуры.
Но стоит отметить еще один немаловажный момент, время регистрации сигналов, это конец двадцатых, начало тридцатых годов... Не был ли тогда нарушен некий запрет на контакт, с целью предотвратить гибель десятков миллионов людей? Имея соответствующий социальный опыт нетрудно спрогнозировать развитие последовавших событий. И нам ведь еще крупно "повезло" - будь атомная бомба сделана раньше на год или два, и обеими сторонами сразу, то, сколько бы еще людей погибло в итоге?
Конечно, категорично утверждать, что представленные материалы есть не что иное, как расшифровка "сообщения" слишком рано, но как мы надеемся, в работе удалось показать, что очевидная гипотеза о соотнесении номеров задержек с номерами звезд в естественном упорядочении приводит к нетривиальным результатам, получившим развитие в научных публикациях.
Также нам кажется, что способ представлений геометрических свойств и фигур непосредственно на звездной сфере, прямо перекликается с идеей Гаусса (1826г), предложившего осуществить гигантские вырубки в сибирской тайге в виде прямоугольного треугольника с длинами сторон относящимися как 3, 4, 5..
Автор выражает признательность за помощь и поддержку Л.М.Гиндилису.
PS :Обсудить работу можно по адресу: http://cmm.univer.omsk.su/gbook
(*)
Project Meta's data. There was registred 37 strong strange 'aletrts' similar famous
signal WOW! (Horowitz&Sagan ApJ, 415, 218-235, 1993).
Five year of project Meta:an all-sky narrow-band radio search for extraterrestrial signals.
1420 MHz
00.82 3.25 7735
00.87 57.5 6942
06.08 -3.5 6782
06.23 9.5 6822
11.58 31.5 6876
21.15 -21.0 6737
21.98 38.5 6894
01.70 33.5 8014
02.90 32.0 8022
03.10 58.0 7847
12.32 16.0 8160
12.73 -12.5 8364
15.55 17.0 8154
19.57 47.5 7916
23.72 8.5 8216
2840 MHz
00.82 3.25 7735
01.30 -22.00 7577
01.83 7.0 7769
05.73 6.0 7326
08.00 -8.50 7415
08.03 11.00 7301
08.08 7.00 7769
08.67 45.75 7159
08.95 -15.75 7452
10.43 -21.25 7481
11.23 58.00 7230
14.30 57.50 7228
14.65 46.50 7164
15.47 -18.00 7599
17.10 2.00 7351
18.05 23.50 7061
18.37 -19.50 7467
18.45 38.50 7127
18.67 -23.25 7493
18.68 -22.25 7565
19.18 -0.50 7699
19.67 -23.00 7560
20.03 30.75 7092
01.30 -22.00 7577
01.83 7.0 7769
05.73 6.0 7326
08.00 -8.50 7415
08.03 11.00 7301
08.08 7.00 7769
08.67 45.75 7159
08.95 -15.75 7452
10.43 -21.25 7481
11.23 58.00 7230
14.30 57.50 7228
14.65 46.50 7164
15.47 -18.00 7599
17.10 2.00 7351
18.05 23.50 7061
18.37 -19.50 7467
18.45 38.50 7127
18.67 -23.25 7493
18.68 -22.25 7565
19.18 -0.50 7699
19.67 -23.00 7560
20.03 30.75 7092
RA DEC Date
00.87 57.5 6942
06.08 -3.5 6782
06.23 9.5 6822
11.58 31.5 6876
21.15 -21.0 6737
21.98 38.5 6894
01.70 33.5 8014
02.90 32.0 8022
03.10 58.0 7847
12.32 16.0 8160
12.73 -12.5 8364
15.55 17.0 8154
19.57 47.5 7916
23.72 8.5 8216
2840 MHz
00.82 3.25 7735
01.30 -22.00 7577
01.83 7.0 7769
05.73 6.0 7326
08.00 -8.50 7415
08.03 11.00 7301
08.08 7.00 7769
08.67 45.75 7159
08.95 -15.75 7452
10.43 -21.25 7481
11.23 58.00 7230
14.30 57.50 7228
14.65 46.50 7164
15.47 -18.00 7599
17.10 2.00 7351
18.05 23.50 7061
18.37 -19.50 7467
18.45 38.50 7127
18.67 -23.25 7493
18.68 -22.25 7565
19.18 -0.50 7699
19.67 -23.00 7560
20.03 30.75 7092
Литература
- Я.Л. Альперт Распространение волн в ионосфере М., Наука, 1985.
- Macvey, J.W., Whispers From Space. Chapter 13 "From What Far Star" P.193. London Abelard Schuman. 1973. ISBN 0 200 72243 3
- C. Stormer, Proceedings of the Royal Society of Edinburgh 50, Part II, no. 15 (1933)
- J B Galle, "Observations relatives a la radio-electricite et a la physique du globe", L'Onde Electrique 9 (1930), pp. 257-265
- J B Galle, G Talon and M Ferrie, "Recherches relatives a la propogation des ondes radioelectriques effectuees a l'occasion de l'eclipse du 9 mai 1929", Comptes Rendus de L'Academie des Sciences, vol. 130 (1930), pp 48-52.
- Lunan. D. INTERSTELLAR CONTACT. Chapter 12. "The News From Bootes". P.223 - 262. Henry Regnery Company: Chicago. 1975 ISBN 0 8092 8258 5 (First published in Great Britain 1974 under the title "Man and the Stars")
- P.Horowitz, C. Sagan Five Years of Project META: All-Sky Narrow-Band Radio Search for Extrateerestrial Signals The Astrophysical Journal, 451:218-235,1993 September 20.
- П.Г. Куликовский Звездная астрономия М., Наука, 1985.
- Гильберт Д., Кон-Фоссен С. Наглядная геометрия М.: Наука, 1981.-344 с.
- Gilbert E.N., Pollak H.O. Steiner minimal trees, SIAM Journal of Applied Mathematics, 16, #1 (1968), pp 1-29.
- Курант Р., Роббинс Г. Что такое математика? ОГИЗ, М.-Л., 1947.
- Faizullin R.T. An Approximations for Genetic Algorithms and Star's Pattern // 1 st On-Line Internet Conference of Soft Computing, Nagoya, Japan, 19-30 Aug 1996. 77-82.
- Файзуллин Р.Т. Конечноэлементные аналогии при моделировании нестандартных сплошных сред //Тр. XIV сессии Международной школы по моделям сплошной среды, Москва:МГУ, 1998. c. 233-238.
- Марочник Л.С., Сучков А.А. Галактика. М.: Наука, 1984, 392 с.
|
Публикации с ключевыми словами:
SETI - задержки радиосигналов - парадокс Штермера
Публикации со словами: SETI - задержки радиосигналов - парадокс Штермера | |
См. также:
Все публикации на ту же тему >> | |































