Астронет > Колебания и волны

по текстам по ключевым словам в глоссарии по сайтам перевод по каталогу

Колебания и волны. Лекции.

В.А.Алешкевич, Л.Г.Деденко, В.А.Караваев (Физический факультет МГУ)
Издательство Физического факультета МГУ, 2001 г. Содержание

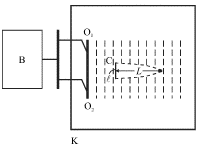
Один из таких опытов выглядит следующим образом (рис. 5.21). В неглубокую кювету К с большой площадью основания наливают воду. Волны на ее поверхности возбуждают с помощью вибратора В, приводящего в периодическое движение два маленьких шарика О₁ и О₂, которые являются точечными источниками волн. Эти шарики слегка погружены в воду и совершают синхронные колебания с частотой $\nu \sim 10^{2} Гц$ в направлении, перпендикулярном поверхности воды. От каждого из точечных источников распространяется волна с длиной $\lambda \sim 3 мм$ и скоростью $c\sim 40 см/с.$ Гребни этих волн в фиксированный момент времени изображены на рисунке пунктиром. В результате наложения волн образуется интерференционная картина, которую удобно наблюдать в стробоскопическом освещении (освещая ее вспышками света, следующими также с частотой $\nu \sim 10^{2} Гц$ ). При таком освещении волны будут казаться практически неподвижными.

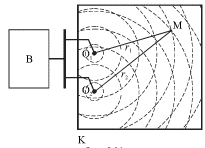Рис. 5.21.

Наиболее сильные возмущения поверхности будут наблюдаться в тех местах, где волны складываются в фазе. Говорят, что здесь располагаются интерференционные максимумы. В местах, куда волны приходят в противофазе, поверхность будет практически не возмущена: здесь располагаются интерференционные минимумы. Возмущение поверхности в произвольной точке M зависит от разности хода $\Delta r = r_{2} - r_{1},$ где $r_{1}$ и $r_{2}$ - расстояния от точки M до соответствующего точечного источника. Действительно, смещение s поверхности жидкости в точке M можно рассматривать как результат наложения двух синусоидальных (т.е. монохроматических) волн, прошедших расстояния $r_{1}$ и $r_{2}$ :

$s(t) = s_{0} \sin (\omega t - kr_{1} - \varphi _{1} ) + s_{0} \sin (\omega t - kr_{2} - \varphi _{2} ).$

(5.44)

Здесь предполагается, что обе волны в точке M имеют одинаковые амплитуды (хотя это и не совсем верно), и постоянные фазовые добавки $\varphi _{1}$ и $\varphi _{2},$ так что их разность $\Delta \varphi = \varphi _{2} - \varphi _{1}$ не зависит от времени.

Выполняя в (5.44) суммирование, получаем:

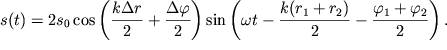$s(t) = 2s_{0} \cos \left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle k\Delta r}}{\displaystyle {\displaystyle 2}}} + {\displaystyle \frac{\displaystyle {\displaystyle \Delta \varphi }}{\displaystyle {\displaystyle 2}}}} \right)\sin \left( {\displaystyle \omega t - {\displaystyle \frac{\displaystyle {\displaystyle k(r_{1} + r_{2} )}}{\displaystyle {\displaystyle 2}}} - {\displaystyle \frac{\displaystyle {\displaystyle \varphi _{1} + \varphi _{2} }}{\displaystyle {\displaystyle 2}}}} \right).$

(5.45)

Если положить для простоты $\Delta \varphi = 0,$ то положение интерференционных максимумов определяется из условия

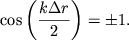$\cos \left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle k\Delta r}}{\displaystyle {\displaystyle 2}}}} \right) = \pm 1.$

(5.46)

Поскольку $k = 2\pi / \lambda,$ то последнему условию соответствует разность хода

$\Delta r = r_{2} - r_{1} = m\lambda,$

(5.47)

где $m = 0, \pm 1, \pm 2, \ldots.$

Каждому максимуму принято присваивать порядковый номер, определяемый соответствующим числом $m$ (максимум нулевого, первого, минус первого и т.д. порядка). Интерференционные минимумы располагаются в тех местах, где

$\Delta r = r_{2} - r_{1} = (2m + 1){\displaystyle \frac{\displaystyle {\displaystyle \lambda }}{\displaystyle {\displaystyle 2}}},$

(5.48)

и так же нумеруются $(m = 0, \pm 1, \pm 2, \ldots).$

Рассмотренная интерференционная картина соответствует идеализированной ситуации. Реальные волны даже в лучшем случае являются квазимонохроматическими. Для таких волн амплитуды $s_{0}$ и фазы $\varphi _{1}$ и $\varphi _{2}$ являются медленно меняющимися функциями времени (заметные изменения этих функций происходят за время $\tau \gg T = {\displaystyle \frac{\displaystyle {\displaystyle 2\pi }}{\displaystyle {\displaystyle \omega }}}$ ). Однако, если оба шарика приводятся в колебательное движение одним вибратором, разность фаз $\Delta \varphi$ в (5.45) остается постоянной, положение интерференционных максимумов задается формулой (5.47) и не зависит от времени.

В практически важных случаях источники интерферирующих волн могут быть независимы. В нашем опыте это можно осуществить, если использовать два вибратора, к каждому из которых присоединен маленький шарик. Тогда разность фаз $\Delta \varphi$ будет также изменяться на масштабе времени $\tau,$ и ее можно записать в виде

$\Delta \varphi (t) = \overline {\displaystyle \Delta \varphi } + \delta (t),$

(5.49)

где $\overline {\displaystyle \Delta \varphi }$ - среднее по времени значение разности фаз, $\delta (t)$ - знакопеременная функция. Считая для простоты в (5.45) $s_{0} = {\displaystyle \rm const},$ приходим к выводу, что интерференционная картина, как целое, будет достаточно хаотично смещаться в разные стороны. Если такую картину снимать на кинопленку со временем экспозиции кадра $\Delta t \gt \tau ,$ то на каждом кадре будет отпечатана усредненная за время $\Delta t$ "размазанная" картина. Она может стать совсем неразличимой, если интерференционные максимумы будут смещаться на величины, равные или превышающие расстояния между соседними максимумами. Такая ситуация достаточно часто встречается при интерференции световых волн. Чтобы полного "смазывания" картины не произошло, очевидно, необходимо выполнение следующего условия:

$|\delta (t)| \ll 2\pi.$

(5.50)

Чем лучше выполняется это неравенство, тем выше качество картины. Так, например, для световых волн $\tau \sim 10^{ - 9}\div 10^{ - 12} с,$ и при визуальном наблюдении (для органов зрения $\Delta t\sim 0,1 с$ ) мы всегда регистрируем "размазанную" интерференционную картину.

С качеством картины напрямую связано понятие когерентности интерферирующих волн. Когерентность характеризуется безразмерным коэффициентом $\gamma$ (степенью когерентности), который может меняться в интервале $0 \lt \gamma \lt 1.$ Чем выше качество картины, тем больше степень когерентности. Для монохроматических волн, конечно, $\gamma = 1.$

Этим замечанием о когерентности волн мы здесь и ограничимся, а детальное описание этого понятия будет дано в курсе "Оптика".

Дифракция волн.

В упрощенном смысле под дифракцией понимают круг явлений, в которых проявляется отступление от прямолинейного распространения волн. Такое понимание дифракции, вообще говоря, неверно, поскольку прямолинейное распространение волн является лишь определенным приближением. Действительно, специфика любого волнового движения проявляется в том, что это движение, возникнув вначале в ограниченной области, стремится распространиться в равной степени во все стороны. Выбором специальной формы этой области можно добиться того, что волна побежит преимущественно в некоторых направлениях. Вдоль одного из таких направлений побежит фрагмент волны, который с определенной точностью можно считать движущимся прямолинейно.

Для наблюдения основных закономерностей дифракции видоизменим характер возбуждения волн на поверхности воды в описанном ранее опыте. В качестве источника волны вместо шариков будем использовать пластину O₁O₂, длина которой $\ell _{0} = (3\div 5) см,$ т.е. заметно превышает длину волны $\lambda \sim 3 мм$ (рис. 5.22). В результате по поверхности воды побежит "плоская" волна в направлении, перпендикулярном пластине. Отчетливо наблюдаются две прямолинейные границы Г₁ и Г₂, отделяющие возмущенную волной и гладкую части поверхности воды. Для этой последней части можно употребить заимствованный из оптики термин: "область геометрической тени". Саму волну часто называют волновым пучком, или лучом. В этом эксперименте можно считать, что волна распространяется прямолинейно и не заходит в область тени. Это связано с тем, что размер ее волнового фронта $\ell _{0} \gg \lambda.$

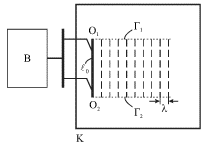Рис. 5.22.

Уменьшим теперь этот размер. Это наиболее просто осуществить, если параллельно пластине O₁O₂ установить две вертикальные стенки С₁ и С₂, расстояние $\ell$ между которыми можно изменять (рис. 5.23).

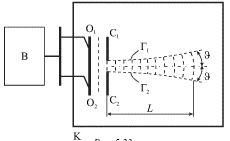Рис. 5.23.

Если сделать $\ell \leq 5\lambda \approx 15 мм,$ то волна начнет постепенно заходить в область тени, а ее фронт будет искривляться. На некотором характерном расстоянии $L$ волновой пучок приобретет заметную угловую расходимость и далее будет распространяться по части поверхности, ограниченной углом $2\vartheta.$ При уменьшении зазора $\ell$ между стенками угол $2\vartheta$ возрастает, а расстояние $L$ уменьшается. Это отступление от прямолинейного распространения является результатом дифракции, существенно тогда, когда $\ell \sim \lambda.$

Не составляет труда оценить величины $\vartheta$ и $L,$ используя подход, предложенный французским ученым О. Френелем в XIX столетии для объяснения дифракции световых волн. Следуя Френелю, участок фронта падающей волны в зазоре между стенками можно рассматривать как цепочку из $N \gg 1$ близко расположенных одинаковых точечных источников $O_{1}, O_{2}, \ldots, O_{N}$ (рис. 5.24).

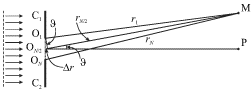Рис. 5.24.

Возмущение в любой точке M поверхности воды есть результат интерференции $N$ волн от этих, так называемых "вторичных" источников, и зависит от разности хода всех интерферирующих волн. В практически важных случаях расстояния $r_{1}, r_{2}, \ldots, r_{N} \gg \ell,$ поэтому отрезки $O_{1}M, O_{2}M, \ldots, O_{N}M$ можно считать параллельными. Понятно, что в точку P, лежащую на оси волнового пучка, интерферирующие волны приходят в фазе и возмущение поверхности в ней будет максимальным. Напротив, в точке M волны могут погасить друг друга, если разность хода $\Delta r = r_{N / 2} - r_{1}$ между волнами от крайнего источника O₁ и среднего источника $O_{N / 2}$ будет равна $\lambda / 2.$ Поскольку эта разность, как видно из рис. 5.24, равна ${\displaystyle \frac{\displaystyle {\displaystyle \ell }}{\displaystyle {\displaystyle 2}}}\sin \vartheta,$ то

$\Delta r = {\displaystyle \frac{\displaystyle {\displaystyle \ell }}{\displaystyle {\displaystyle 2}}}\sin \vartheta = {\displaystyle \frac{\displaystyle {\displaystyle \lambda }}{\displaystyle {\displaystyle 2}}}.$

(5.51)

Аналогично, в противофазе будут приходить волны и от других пар источников $(O_{2}, O_{N / 2 + 1};\; O_{3}, O_{N / 2 + 2};\; \ldots;\; O_{N / 2 - 1}, O_{N}).$ Говорят, что в точке M будет наблюдаться первый минимум дифракционной картины. Не составляет труда написать условие, подобное (5.51), и для других минимумов. Однако, как показывает строгий анализ, более 90% всей энергии переносится волной в пределах угла $2\vartheta.$ Поэтому на рисунке (5.23) границы Г₁ и Г₂ весьма условны и очерчивают лишь основную, наиболее энергоемкую часть пучка.

Для оценки дифракционной расходимости волновых пучков используется угол $\vartheta,$ который при $\ell \gg \lambda$ оценивается согласно (5.51) по формуле

$\vartheta \approx {\displaystyle \frac{\displaystyle {\displaystyle \lambda }}{\displaystyle {l}}}.$

(5.52)

Такую расходимость пучок приобретает на некотором характерном расстоянии $L.$ Его можно легко оценить из рисунка 5.25, на котором пунктиром изображены асимптоты к границам Г₁ и Г₂. Будем условно считать, что на расстоянии $L$ поперечный размер пучка удвоился и стал равным $2\ell.$ Тогда с учетом (5.52) мы можем записать:

$\vartheta = {\displaystyle \frac{\displaystyle {\displaystyle \ell }}{\displaystyle {l}}} = {\displaystyle \frac{\displaystyle {\displaystyle \lambda }}{\displaystyle {\displaystyle \ell }}}.$

(5.53)

Отсюда

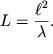$L = {\displaystyle \frac{\displaystyle {\displaystyle \ell ^{2}}}{\displaystyle {\displaystyle \lambda }}}.$

(5.54)

Величина $L$ называется дифракционной длиной пучка с длиной волны $\lambda$ и поперечным размером $\ell.$ Она определяет масштаб расстояний, на которых развивается заметная дифракция пучка.

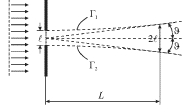Рис. 5.25.

Сделаем некоторые оценки. В опыте, изображенном на рисунке (5.22), $\ell = 5 см,\; \lambda = 3 мм,$ и $L\sim 80 см.$ Это означает, что в кювете дифракция просто не успевает заметно развиться. При уменьшении $\ell$ (рис. 5.23) до величины $\ell = 5\lambda = 15 мм,$ дифракционная длина пучка $L = 7,5 см,$ и дифракция становится отчетливо видна.

Если на пути волнового пучка поставить препятствие - стенку С (рис. 5.26), то сразу за стенкой будет тень, однако волна, пройдя расстояние $\sim L = \ell ^{2} / \lambda,$ обогнет препятствие. Иллюстрацией к сказанному является, например, возможность услышать звуковой сигнал автомобиля, находясь позади небольшого строения. Однако за многоэтажный дом звук практически не проникает.

Рис. 5.26.

Назад| Вперед

Публикации с ключевыми словами: колебания - волны Публикации со словами: колебания - волны
См. также: Эхо из глубин красного гиганта

Обсудить эту публикацию

Версия для печати

Астрометрия - Астрономические инструменты - Астрономическое образование - Астрофизика - История астрономии - Космонавтика, исследование космоса - Любительская астрономия - Планеты и Солнечная система - Солнце