Колебания и волны. Лекции.
В.А.Алешкевич, Л.Г.Деденко, В.А.Караваев (Физический факультет МГУ)Издательство Физического факультета МГУ, 2001 г. Содержание
В последние годы была выявлена детальная структура мантии Земли. На рис. 5.3
показано распределение скорости ![]() в мантии, из которого можно
сделать заключение о её структуре. Земная кора и верхний слой мантии до
глубины
в мантии, из которого можно
сделать заключение о её структуре. Земная кора и верхний слой мантии до
глубины ![]() образуют наружную зону - литосферу, или
литосферную плиту. Эта жесткая плита расколота примерно на 10 больших плит,
по границам которых расположено подавляющее число очагов землетрясений. Под
жесткой литосферной плитой на глубинах
образуют наружную зону - литосферу, или
литосферную плиту. Эта жесткая плита расколота примерно на 10 больших плит,
по границам которых расположено подавляющее число очагов землетрясений. Под
жесткой литосферной плитой на глубинах ![]() расположен слой
повышенной текучести, называемый астеносферой. Из-за её малой вязкости
расположен слой
повышенной текучести, называемый астеносферой. Из-за её малой вязкости ![]() литосферные плиты как бы плавают в
"астеносферном океане" Земли. В астеносфере, где температура вещества
близка к температуре плавления, скорости волн понижены. Начиная с
литосферные плиты как бы плавают в
"астеносферном океане" Земли. В астеносфере, где температура вещества
близка к температуре плавления, скорости волн понижены. Начиная с ![]() скорости возрастают из-за увеличения давления. При
скорости возрастают из-за увеличения давления. При ![]() возрастание скорости есть результат фазовых переходов
(минералы оливины переходят в шпинелевую модификацию), а на глубинах
возрастание скорости есть результат фазовых переходов
(минералы оливины переходят в шпинелевую модификацию), а на глубинах ![]() скорость возрастает из-за роста давления. На глубинах
скорость возрастает из-за роста давления. На глубинах ![]() расположена вторая зона фазовых переходов, однако остается
открытым вопрос о том, какие конкретно переходы ответственны за быстрый рост
скорости.
расположена вторая зона фазовых переходов, однако остается
открытым вопрос о том, какие конкретно переходы ответственны за быстрый рост
скорости.
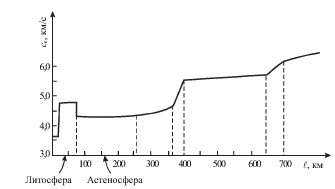 |
| Рис. 5.3. |
На рис. 5.4 изображен разрез Земли, построенный в соответствии с современными сейсмическими данными.
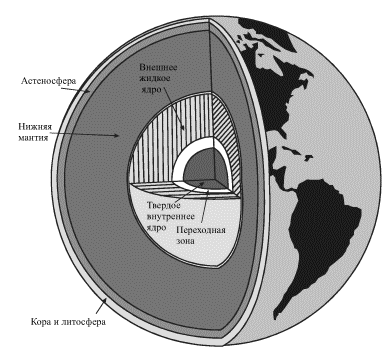 |
| Рис. 5.4. |
При распространении объемной сейсмической волны в трехмерном случае амплитуда уменьшается с расстоянием r, пройденным волной от точечного источника. Уравнение такой волны, называемой сферической, имеет вид:
| (5.4) |
Из этого уравнения видно, что амплитуда волны убывает, во-первых, из-за ее
геометрического расхождения во все стороны от эпицентра; это убывание
происходит обратно пропорционально пройденному волной расстоянию ![]() Во-вторых, амплитуда волны убывает из-за перехода части энергии волны в
тепло вследствие неидеальной упругости земных недр. Это ослабление
характеризуется коэффициентом затухания
Во-вторых, амплитуда волны убывает из-за перехода части энергии волны в
тепло вследствие неидеальной упругости земных недр. Это ослабление
характеризуется коэффициентом затухания ![]() Коэффициент
Коэффициент ![]() пропорционален частоте сейсмической волны, поэтому короткие волны затухают
быстрее длинных. Расчет показывает, что для коэффициентов затухания s- и
p-волн могут быть записаны соотношения
пропорционален частоте сейсмической волны, поэтому короткие волны затухают
быстрее длинных. Расчет показывает, что для коэффициентов затухания s- и
p-волн могут быть записаны соотношения
Частоты объемных сейсмических волн лежат в инфразвуковом диапазоне
![]() Следовательно, для волн с частотой
Следовательно, для волн с частотой ![]() уменьшение амплитуды в е раз у поперечной волны происходит на пути ~ 1000 км, а у продольной волны - на пути ~ 4000 км.
уменьшение амплитуды в е раз у поперечной волны происходит на пути ~ 1000 км, а у продольной волны - на пути ~ 4000 км.
Помимо бегущих волн, в объеме Земли могут наблюдаться и стоячие волны, когда вся Земля колеблется, как целое, с различными частотами, соответствующими различным модам колебаний. Конфигурации этих мод относятся к двум основным типам: сфероидальные колебания (наибольший период ~ 55 мин., частота ~ 3*10-4 Гц) и торсионные (крутильные) колебания (наибольший период ~ 44 мин., частота ~ 3,8*10-4 Гц). В настоящее время спектр этих колебаний насчитывает несколько тысяч экспериментально обнаруженных частот.
Поверхностные сейсмические волны.
Наряду с объемными, по Земле могут распространятся и поверхностные волны. Эти волны бывают двух типов и называются волнами Рэлея и Лява. Они были теоретически предсказаны Дж. Рэлеем в 1855 г. и Лявом в 1911 г. В Рэлеевской волне частицы грунта смещаются в вертикальной плоскости, ориентированной вдоль направления распространения волн, а траектории их движения представляют собой эллипсы (см. далее гравитационные волны на поверхности жидкости). В волне Лява частицы движутся в горизонтальной плоскости поперек направления распространения волны.
Длины поверхностных волн ![]() возбуждаемых при землетрясении, лежат в
интервале от десятков до многих сотен километров. В поверхностных волнах
амплитуда убывает с глубиной, и на глубине
возбуждаемых при землетрясении, лежат в
интервале от десятков до многих сотен километров. В поверхностных волнах
амплитуда убывает с глубиной, и на глубине ![]() колебания
мантии малы. Поэтому с помощью таких волн можно исследовать лишь наружные
слои Земли.
колебания
мантии малы. Поэтому с помощью таких волн можно исследовать лишь наружные
слои Земли.
Из-за двумерного распространения амплитуда поверхностных волн убывает
медленнее (обратно пропорционально ![]() ), чем у объемных волн.
Поэтому такие волны могут по несколько раз обегать вокруг земного шара.
Скорость поверхностных волн зависит от частоты, т. е. они обладают
дисперсией.
), чем у объемных волн.
Поэтому такие волны могут по несколько раз обегать вокруг земного шара.
Скорость поверхностных волн зависит от частоты, т. е. они обладают
дисперсией.
На рисунке 5.5 показаны зависимости групповых скоростей волн Рэлея ![]() и Лява
и Лява ![]() от периода колебания волны. Легко видеть, что волны Лява
распространяются быстрее волн Рэлея. Отметим, что на рис. 5.5 показаны
от периода колебания волны. Легко видеть, что волны Лява
распространяются быстрее волн Рэлея. Отметим, что на рис. 5.5 показаны
![]() и
и ![]() лишь для волн, амплитуды которых определенным образом
убывают с глубиной. Возможны поверхностные волны и с другими распределениями
амплитуд по глубине.
лишь для волн, амплитуды которых определенным образом
убывают с глубиной. Возможны поверхностные волны и с другими распределениями
амплитуд по глубине.
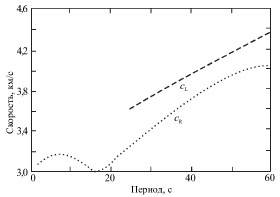 |
| Рис. 5.5. |
Сейсмические волны можно вызвать при помощи взрыва. Небольшие взрывы используются в инженерной сейсмологии для проведения разведки полезных ископаемых (нефти, руды, газа и т. д.). Подземные ядерные взрывы создают интенсивные волны, которые можно регистрировать на любых расстояниях. Это дает возможность надежно проводить контроль над подземными ядерными испытаниями.
Волны в жидкостях и газах.
В жидкостях и газах возможны лишь деформации
сжатия и растяжения, поэтому в них могут распространятся только продольные
волны. Хотя мы ранее и рассчитывали скорость распространения возмущений в
газе, тем не менее вычислим скорость распространения продольных волн с
использованием волнового уравнения. Последнее может быть получено из (4.74),
в котором ![]() следует заменить величиной
следует заменить величиной ![]() где
где ![]() - давление в волне,
- давление в волне, ![]() - равновесное давление в среде,
- равновесное давление в среде,
![]() - возмущение давления. Тогда мы можем записать
- возмущение давления. Тогда мы можем записать
![$ dm{\displaystyle \frac{\displaystyle {\displaystyle \partial ^{2}s}}{\displaystyle {\displaystyle \partial t^{2}}}} = [ - \delta p(x + dx,t) + \delta p(x,t)]S. $](http://images.astronet.ru/pubd/2002/04/09/0001175791/tex/formula904.gif) | (5.5) |
Чтобы из (5.5) получить волновое уравнение, необходимо знать материальное уравнение среды
| (5.6) |
Качественно эта зависимость изображена на рис. 5.6. При очень малых
возмущениях плотности ![]() и
давления
и
давления ![]() из (5.6) получаем:
из (5.6) получаем:
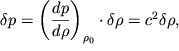 | (5.7) |
где введено обозначение
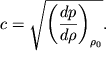 | (5.8) |
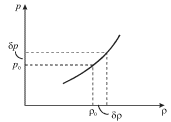 |
| Рис. 5.6. |
С учетом (4.69) и (4.72) возмущения плотности ![]() в (5.7) связаны
со смещением s соотношением:
в (5.7) связаны
со смещением s соотношением:
| (5.9) |
Следовательно, (5.7) примет вид:
| (5.10) |
Подставляя (5.10) в (5.5), записывая ![]() и переходя к
пределу при
и переходя к
пределу при ![]() получим волновое уравнение
получим волновое уравнение
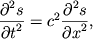 | (5.11) |
из которого сразу видно, что скорость волны задается выражением (5.8) и не
зависит от частоты (дисперсия отсутствует). Естественно, что с такой
скоростью распространяются волны с длиной волны ![]() превосходящей
длину свободного пробега молекул в газе или межатомные расстояния в
жидкостях
превосходящей
длину свободного пробега молекул в газе или межатомные расстояния в
жидкостях ![]() В этом случае жидкость и газ могут рассматриваться как
сплошные среды. Для волн высоких частот, когда
В этом случае жидкость и газ могут рассматриваться как
сплошные среды. Для волн высоких частот, когда ![]() возникает дисперсия, а волны с длиной
возникает дисперсия, а волны с длиной ![]() распространяться
вообще не могут.
распространяться
вообще не могут.
Упругие волны в жидкостях и газах, как, впрочем, и в твердых телах,
называются акустическими, а раздел физики, который их изучает - акустикой.
Частоты этих волн лежат в диапазоне от долей герца (инфразвук) до 1013
Гц (гиперзвук). Этим частотам соответствуют длины волн ![]() от
десятков километров до нескольких ангстрем. Значения скоростей (фазовых и
групповых) для разных сред лежат в диапазоне от долей до десятков км/с.
от
десятков километров до нескольких ангстрем. Значения скоростей (фазовых и
групповых) для разных сред лежат в диапазоне от долей до десятков км/с.
Для воздуха материальное уравнение (5.6) является уравнением адиабаты и в акустике обычно записывается в виде (см. также предыдущие лекции):
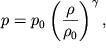 | (5.12) |
где ![]() - показатель адиабаты.
- показатель адиабаты.
Тогда из (5.8) скорость волны (в акустике употребляют термин "скорость звука") в газе получается равной
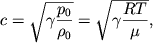 | (5.13) |
где ![]() - молярная масса газа.
- молярная масса газа.
Скорость звука зависит, таким образом, от рода газа и по порядку величины совпадает со средней скоростью теплового движения молекул.
Для жидкости материальным уравнением является полуэмпирическое уравнение Тета:
![$ p = p_{вн} {\displaystyle \left[ {\displaystyle \left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle \rho }}{\displaystyle {\displaystyle \rho _{0} }}}} \right)^{\Gamma } - 1} \right]}, $](http://images.astronet.ru/pubd/2002/04/09/0001175791/tex/formula923.gif) | (5.14) |
где ![]() - характерное внутреннее давление, обусловленное
межмолекулярным взаимодействием (оно составляет для большинства жидкостей
без пузырьков и различных включений несколько тысяч атмосфер). Параметр
- характерное внутреннее давление, обусловленное
межмолекулярным взаимодействием (оно составляет для большинства жидкостей
без пузырьков и различных включений несколько тысяч атмосфер). Параметр
![]() имеет порядок нескольких единиц (например, для воды
имеет порядок нескольких единиц (например, для воды ![]() ).
).
В таблице приведены значения скорости звука, измеренные в некоторых газах
(при температуре ![]() ) и жидкостях.
) и жидкостях.
| Газы | Скорость звука, м/с | Жидкости | Скорость звука, м/с |
| Водород | 1265 | Вода | 1490 |
| Гелий | 965 | Этил. спирт | 1180 |
| Азот | 334 | Водород | 1127 |
| Воздух | 331 | Кислород | 911 |
| Кислород | 316 | Азот | 867 |
| Углекислота | 216 | Гелий | 180 |
|
Публикации с ключевыми словами:
колебания - волны
Публикации со словами: колебания - волны | |
|
См. также:
| |