Колебания и волны. Лекции.
В.А.Алешкевич, Л.Г.Деденко, В.А.Караваев (Физический факультет МГУ)Издательство Физического факультета МГУ, 2001 г. Содержание
Вынужденные колебания с произвольной частотой.
Будем искать решение уравнения (2.10) в комплексном виде:
| (2.26) |
Вынуждающую силу в правой части (2.10) также запишем в комплексной форме:
| (2.27) |
где ![]() - действительное число, поскольку для простоты
мы положили, что начальная фаза в выражении для силы (2.5) равна нулю.
- действительное число, поскольку для простоты
мы положили, что начальная фаза в выражении для силы (2.5) равна нулю.
Тогда уравнение (2.10) можно записать в виде:
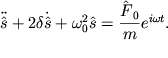 | (2.28) |
Комплексную амплитуду ![]() легко
находим подстановкой (2.26) в (2.28):
легко
находим подстановкой (2.26) в (2.28):
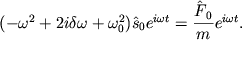 | (2.29) |
Отсюда получаем:
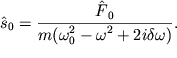 | (2.30) |
Из (2.30) нетрудно найти амплитуду колебаний ![]()
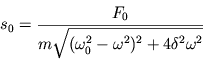 | (2.31) |
и фазу ![]()
| (2.32) |
полностью определяющие вынужденные колебания (2.25).
Зависимость амплитуды ![]() от частоты
от частоты ![]() задаваемая формулой
(2.31), называется амплитудно-частотной характеристикой (АЧХ), а
зависимость
задаваемая формулой
(2.31), называется амплитудно-частотной характеристикой (АЧХ), а
зависимость ![]() описываемая формулой (2.32),
называется фазо-частотной характеристикой (ФЧХ). На рис. 2.3 изображена
АЧХ, которая отображает нарастание амплитуды
описываемая формулой (2.32),
называется фазо-частотной характеристикой (ФЧХ). На рис. 2.3 изображена
АЧХ, которая отображает нарастание амплитуды ![]() при приближении
при приближении ![]() к
к ![]() Это явление получило название резонанса смещений.
Интересно, что максимальное значение амплитуды, в
Это явление получило название резонанса смещений.
Интересно, что максимальное значение амплитуды, в ![]() раз превосходящее
статическое смещение
раз превосходящее
статическое смещение ![]() достигается на частоте
достигается на частоте
| (2.33) |
которая несколько меньше как собственной частоты ![]() так и
частоты затухающих колебаний
так и
частоты затухающих колебаний ![]() Для
практических целей для частот
Для
практических целей для частот ![]() лежащих вблизи частоты
лежащих вблизи частоты ![]() формула (2.31) может быть значительно упрощена. Так, можно положить
формула (2.31) может быть значительно упрощена. Так, можно положить
| (2.34) | |
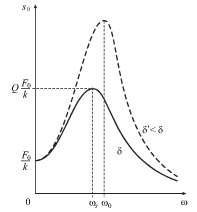 |
| Рис. 2.3. |
С учетом приближений (2.34) формула (2.31) примет вид:
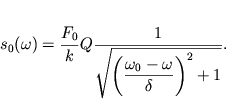 | (2.35) |
В физике безразмерную функцию
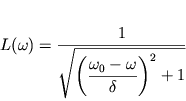 | (2.36) |
называют Лоренцевой, а график этой функции называют Лоренцевым контуром.
Ширину ![]() этого контура, определяющую остроту резонанса,
находят из условия убывания вдвое энергии колебательной системы,
пропорциональной квадрату амплитуды
этого контура, определяющую остроту резонанса,
находят из условия убывания вдвое энергии колебательной системы,
пропорциональной квадрату амплитуды ![]() в (2.35), что
эквивалентно приближенному соотношению
в (2.35), что
эквивалентно приближенному соотношению
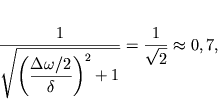 | (2.37) |
которое поясняется рисунком 2.4. При этом условии ![]() т.е.
т.е. ![]() Ширина Лоренцева
контура характеризует полосу пропускания колебательной системы, т.е. такую
область частот внешней силы, для которых система эффективно откликается на
гармоническое внешнее воздействие. Легко видеть, что добротность системы
равна
Ширина Лоренцева
контура характеризует полосу пропускания колебательной системы, т.е. такую
область частот внешней силы, для которых система эффективно откликается на
гармоническое внешнее воздействие. Легко видеть, что добротность системы
равна
| (2.38) |
т.е. обратно пропорциональна полосе пропускания.
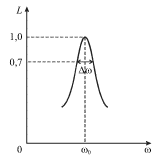 |
| Рис. 2.4. |
С уменьшением коэффициента ![]() АЧХ меняет свою форму, как это
изображено пунктиром на рис. 2.3 для
АЧХ меняет свою форму, как это
изображено пунктиром на рис. 2.3 для ![]() Полоса
пропускания
Полоса
пропускания ![]() уменьшается, добротность
уменьшается, добротность ![]() возрастает, и
резонанс становится более острым.
возрастает, и
резонанс становится более острым.
Фазо-частотная характеристика для двух различных коэффициентов затухания
изображена на рис. 2.5. Физическое содержание зависимости ![]() мы подробно обсудили для трех различных режимов вынужденных
колебаний. Отметим лишь, что с уменьшением затухания
мы подробно обсудили для трех различных режимов вынужденных
колебаний. Отметим лишь, что с уменьшением затухания ![]() кривая
кривая
![]() становится более "чувствительной" к изменению
частоты вблизи резонанса.
становится более "чувствительной" к изменению
частоты вблизи резонанса.
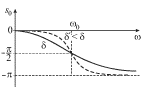 |
| Рис. 2.5. |
Наряду с резонансом смещений, можно говорить о резонансе скоростей ![]() и резонансе ускорений
и резонансе ускорений ![]()
Скорость колеблющейся массы равна:
| (2.39) |
а ее ускорение:
| (2.40) |
т.е. амплитудно-частотная характеристика для скорости получается умножением
АЧХ (2.31) на ![]() а для ускорения - на
а для ускорения - на ![]() :
:
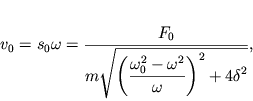 |
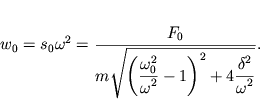 |
На рис. 2.6 изображены частотные зависимости амплитуд скорости ![]() и ускорения
и ускорения ![]()
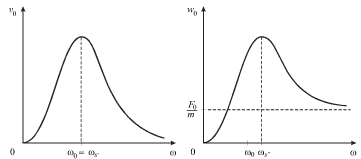 |
| Рис. 2.6. |
Характерно, что резонанс скорости происходит на частоте ![]() а резонанс ускорения - при
а резонанс ускорения - при ![]() Отметим, что все резонансные частоты связаны между собой:
Отметим, что все резонансные частоты связаны между собой:
| (2.41) |
Отметим также, что по причинам, рассмотренным ранее, в области низких частот
малы как ускорение, так и скорость. В области высоких частот ускорение
конечно ![]() и обеспечивается лишь
внешней силой. Однако скорость по-прежнему незначительна, поскольку тело не
успевает разогнаться.
и обеспечивается лишь
внешней силой. Однако скорость по-прежнему незначительна, поскольку тело не
успевает разогнаться.
Не представляет труда нарисовать самостоятельно фазо-частотные
характеристики для скорости и для ускорения, пользуясь формулами (2.39) и
(2.40), поскольку они получаются простым сдвигом ФЧХ для смещения (2.32),
изображенной на рис. 2.5, вверх соответственно на ![]() или на
или на ![]()
В заключение рассмотрим вопрос о подводе энергии к осциллятору при произвольной частоте вынуждающей силы. Средняя за период мощность этой силы равна
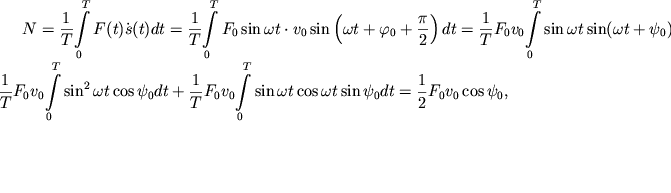 |
где ![]() - сдвиг фаз между скоростью и силой. Мы видим, что максимум подводимой к осциллятору мощности
достигается на частоте
- сдвиг фаз между скоростью и силой. Мы видим, что максимум подводимой к осциллятору мощности
достигается на частоте ![]() поскольку при этом максимальны и
амплитуда скорости
поскольку при этом максимальны и
амплитуда скорости ![]() и
и ![]() При других
частотах вынуждающей силы эта мощность быстро уменьшается и стремится к
нулю, как при
При других
частотах вынуждающей силы эта мощность быстро уменьшается и стремится к
нулю, как при ![]() так и при
так и при ![]()
|
Публикации с ключевыми словами:
колебания - волны
Публикации со словами: колебания - волны | |
|
См. также:
| |