4.3.3. Прямая и обратная задачи над намагниченным вертикальным бесконечно длинным столбом (стержнем).
1. Прямая задача. Пусть на глубинеНеобходимо найти напряженность поля вдоль профиля x над телом. Потенциал от верхнего полюса столба в точке P будет равен потенциалу точечной массы (см.2.4):
| (2.7) |
Составляющие поля выражаются производными потенциала по соответствующим осям координат:
| (2.8) |
Используя полученные формулы,
можно построить графики напряженности поля (рис. 2.4). Легко видеть,
что над столбом будут максимумы ![]() и
и ![]() , а значения их будут одного знака, положительные при вертикальной
, а значения их будут одного знака, положительные при вертикальной
![]() . Горизонтальная составляющая (
. Горизонтальная составляющая (![]() ) слева
будет иметь максимум, а справа - минимум. Вдалеке от столба аномалии
исчезают. В плане над таким столбом изолинии
) слева
будет иметь максимум, а справа - минимум. Вдалеке от столба аномалии
исчезают. В плане над таким столбом изолинии ![]() и
и ![]() будут иметь вид концентрических окружностей
одного знака.
будут иметь вид концентрических окружностей
одного знака.
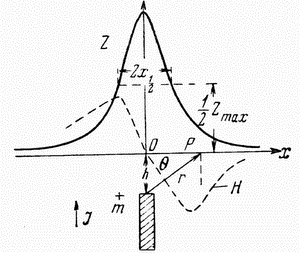 |
| Рис. 2.4. Магнитное поле вертикального бесконечно длинного столба |
2. Обратная задача.
Решение уравнений (2.8) дает возможность по характерным точкам на
графиках определить глубину залегания верхней кромки вертикального
бесконечно длинного столба ( ![]() ). Так центр столба находится
в точке, где
). Так центр столба находится
в точке, где ![]() а
а ![]()
Для точек, удаленных на расстояния ![]() от начала координат, в которых
от начала координат, в которых ![]() равно половине максимального
равно половине максимального
Решив это уравнение, получим ![]() h. Аналогичным образом находятся связи и между другими характерными
точками
h. Аналогичным образом находятся связи и между другими характерными
точками ![]() ,
, ![]() (экстремумы на составляющей
(экстремумы на составляющей
![]() ),
), ![]() (абсциссы точек пересечения
(абсциссы точек пересечения
![]() и
и ![]() ). В результате получаются следующие формулы
для расчета
). В результате получаются следующие формулы
для расчета ![]() по абсолютным значениям этих параметров:
по абсолютным значениям этих параметров:
| (2.9) |
Зная ![]() , можно оценить величину магнитной массы:
, можно оценить величину магнитной массы:
Так как
Отсюда, если известно \kappa по измерениям на образцах,
можно определить площадь поперечного сечения столба ( ![]() ).
).
4.3.4. Прямая и обратная задачи над вертикально намагниченным шаром.
1. Прямая задача. Пусть вертикально намагниченный шар с центром на глубине| (2.10) |
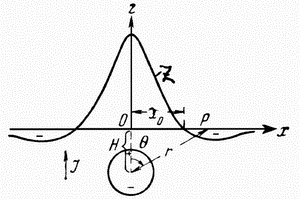 |
| Рис. 2.5. Магнитное поле шара |
Отсюда, взяв производные, найдем элементы магнитного
поля шара:
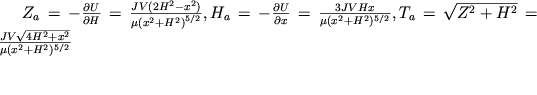 | (2.11) |
Анализ этих формул и построенных по ним графиков показывает, что над центром шара (
Таким образом, в плане над шаром изолинии
![]() и
и ![]() будут иметь вид концентрических
окружностей. При этом изолинии
будут иметь вид концентрических
окружностей. При этом изолинии ![]() будут двух знаков,
а
будут двух знаков,
а ![]() - одного.
- одного.
2. Обратная задача. Решение уравнений (2.11) теми же приемами, что и для столба, дает возможность по характерным точкам на графиках найти глубину центра вертикально намагниченного шара:
| Ha=1,8|xZ1/2|=1,8|xZH|=1,5|xT1/2|=0,7|xZ0|=0,5|xZmin|= | (2.12) |
где ![]() и
и ![]() - абсциссы точек половины
- абсциссы точек половины
![]() - точки с
- точки с
![]() точки с
точки с ![]()
Зная ![]() , можно оценить магнитную массу шара
(
, можно оценить магнитную массу шара
( ![]() ):
):
Отсюда, так как
4.3.5. Прямая и обратная задачи над вертикально намагниченным тонким пластом бесконечного простирания и глубины.
Пусть на глубине ![]() параллельно оси
y расположен бесконечно длинный вертикальный пласт (с толщиной
параллельно оси
y расположен бесконечно длинный вертикальный пласт (с толщиной
![]() , меньшей глубины залегания), намагниченный вертикально
(рис. 2.6). Определим для простоты лишь
, меньшей глубины залегания), намагниченный вертикально
(рис. 2.6). Определим для простоты лишь ![]() вдоль
оси
вдоль
оси ![]() .
.
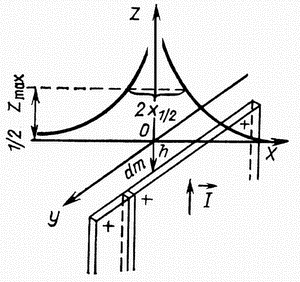 |
| Рис. 2.6. Магнитное поле тонкого пласта бесконечного простирания |
Поскольку нижняя часть пласта расположена глубоко,
то влияние магнитного полюса глубоких частей пласта будет мало, и
можно считать, что магнитные массы сосредоточены вдоль поверхности
в виде линейных полюсов. Магнитная масса единицы длины пласта равна
![]()
Разобьем пласт на множество
тонких "столбов". Тогда притяжение пласта будет складываться из притяжения
всех элементарных столбов, а вертикальная составляющая его магнитного
притяжения будет равна интегралу в пределах от ![]() до
до ![]() (по оси
(по оси ![]() ) выражения для притяжения элементарного столба.
Потенциал элементарного тонкого столба равен
) выражения для притяжения элементарного столба.
Потенциал элементарного тонкого столба равен
,
а вертикальная составляющая ![]() ,
,
откуда ![]() равно
равно
| (2.13) |
График ![]() будет иметь максимум
над центром пласта и асимптотически стремиться к нулю при удалении
от пласта. В плане над пластом будут вытянутые аномалии
будет иметь максимум
над центром пласта и асимптотически стремиться к нулю при удалении
от пласта. В плане над пластом будут вытянутые аномалии ![]() одного знака. Анализируя формулу (2.13), можно найти связи
между глубиной залегания пласта (
одного знака. Анализируя формулу (2.13), можно найти связи
между глубиной залегания пласта ( ![]() ) и
) и ![]() ,
т.е. абсциссой графика, где
,
т.е. абсциссой графика, где ![]()
Магнитная масса единицы длины равна ![]() . Заменив
. Заменив ![]() , получим
, получим
![]() .
Зная
.
Зная ![]() и
и ![]() , можно рассчитать
ширину пласта.
, можно рассчитать
ширину пласта.
|
Публикации с ключевыми словами:
геофизика - Земля - земная кора
Публикации со словами: геофизика - Земля - земная кора | |
См. также:
Все публикации на ту же тему >> | |