Радиационные дисконы - новые астрофизические объекты
В.В.ЖЕЛЕЗНЯКОВ
Нижегородский государственный университет
|
Рассмотрено строение астрофизических объектов нового типа - радиационных дисконов. Они включают в себя горячий белый карлик или нейтронную звезду с сильным магнитным полем, где под действием давления, вызываемого излучением на циклотронных частотах, происходят истечение вещества и накопление его в магнитосфере вокруг звезды. Обсуждаются кандидаты в дисконы - магнитные белые карлики GD229, PG1031+234 и GrW+70°8247. |
Что такое радиационный дискон
Наряду с обычными звездами, свет которых можно видеть невооруженным глазом, в нашей и других галактиках существуют так называемые вырожденные звезды. В таких звездах вещество или его отдельные компоненты в основном состоят из вырожденного газа, движение частиц в котором описывается не классическими, а квантовыми законами. Давление в такого рода газах существенно возрастает по сравнению с давлением классического газа в обычных звездах. Это делает возможным образование звезд малых размеров - белых карликов и нейтронных звезд, - в которых огромные силы гравитации уравновешиваются сильным давлением вырожденного газа. Размеры белых карликов сравнимы с размерами Земли, а нейтронных звезд еще меньше, всего лишь 10-15 км, в то время как их массы порядка массы Солнца. У многих вырожденных звезд существуют сильные магнитные поля, достигающие 107-109 Гс у белых карликов и 1011-1013 Гс у нейтронных звезд.
Столь сильные магнитные поля резко меняют характер взаимодействия плазмы в окрестности звезды с ее излучением. Благодаря магнитному полю возникает сильное циклотронное рассеяние излучения в плазме на частоте вращения электронов в магнитном поле - электронной гирочастоте (циклотронной частоте) ![]() и ее гармониках
и ее гармониках ![]() (B - магнитное поле, e и m - заряд и масса электрона, c - скорость света, s - целое положительное число). Этот эффект приводит к формированию циклотронных особенностей в спектрах вырожденных звезд. Такие особенности в виде линий и полос наблюдались (и объяснялись теоретически) в оптических спектрах магнитных белых карликов (как изолированных, так и находящихся в двойных системах, где происходит аккреция - перетекание вещества с обычной звезды на вырожденную), в спектрах рентгеновских пульсаров и космических гамма-всплесков. Кроме того, сильные магнитные поля вырожденных звезд могут влиять на движение плазмы. Во-первых, сильное магнитное поле определяет картину течений вещества и существенно влияет на характер аккреции на звезду и истечения вещества с ее поверхности. Во-вторых, при поглощении или рассеянии излучения на циклотронных частотах плазме передается его импульс, что приводит к появлению силы давления излучения. В случае, если эта сила превышает силу тяжести, можно ожидать, что динамика плазмы в окрестности магнитных вырожденных звезд в значительной степени определяется радиационным давлением, подобно тому как параметры атмосфер горячих звезд-гигантов определяются давлением излучения в резонансных линиях ионов. Давление циклотронного излучения может порождать плазменные течения типа звездного ветра с поверхности и разгонять вещество в таких течениях до субрелятивистских скоростей. Оно способно тормозить вещество в аккреционной колонке рентгеновских пульсаров и формировать плазменные структуры особого типа в магнитосферах одиночных звезд. Последней проблеме и посвящена статья.
(B - магнитное поле, e и m - заряд и масса электрона, c - скорость света, s - целое положительное число). Этот эффект приводит к формированию циклотронных особенностей в спектрах вырожденных звезд. Такие особенности в виде линий и полос наблюдались (и объяснялись теоретически) в оптических спектрах магнитных белых карликов (как изолированных, так и находящихся в двойных системах, где происходит аккреция - перетекание вещества с обычной звезды на вырожденную), в спектрах рентгеновских пульсаров и космических гамма-всплесков. Кроме того, сильные магнитные поля вырожденных звезд могут влиять на движение плазмы. Во-первых, сильное магнитное поле определяет картину течений вещества и существенно влияет на характер аккреции на звезду и истечения вещества с ее поверхности. Во-вторых, при поглощении или рассеянии излучения на циклотронных частотах плазме передается его импульс, что приводит к появлению силы давления излучения. В случае, если эта сила превышает силу тяжести, можно ожидать, что динамика плазмы в окрестности магнитных вырожденных звезд в значительной степени определяется радиационным давлением, подобно тому как параметры атмосфер горячих звезд-гигантов определяются давлением излучения в резонансных линиях ионов. Давление циклотронного излучения может порождать плазменные течения типа звездного ветра с поверхности и разгонять вещество в таких течениях до субрелятивистских скоростей. Оно способно тормозить вещество в аккреционной колонке рентгеновских пульсаров и формировать плазменные структуры особого типа в магнитосферах одиночных звезд. Последней проблеме и посвящена статья.
Предположим, что в верхних слоях фотосферы магнитного белого карлика или нейтронной звезды давление циклотронного излучения превышает силу тяжести и приводит к истечению плазмы с поверхности звезды. Магнитное давление вокруг таких звезд много больше динамического давления движущейся плазмы. Поэтому вещество из фотосферы магнитной вырожденной звезды не может истекать свободно - оно, как правило, движется вдоль силовых линий магнитного поля. Основная часть "выметаемой" давлением излучения фотосферной плазмы не в состоянии деформировать или разомкнуть силовые линии магнитного поля (которое для простоты считаем дипольным) и накапливается в магнитосфере. Лишь относительно малая часть силовых линий, примыкающих к магнитной оси, может быть разомкнута плазменным течением.
Изложенные соображения легли в основу гипотезы [1] о возможном существовании новых астрофизических объектов - радиационных дисконов (схема на рис. 1).
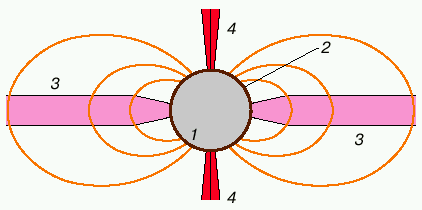 |
| Рис. 1.Первоначальная модель радиационного дискона [1]: 1 - горячая изолированная магнитная вырожденная звезда (белый карлик или нейтронная звезда); 2 - фотосфера, из которой истекает плазменный ветер, порождаемый циклотронным излучением; 3 - диск вблизи магнитного экватора в закрытой части магнитосферы; 4 - ускоряемый давлением излучения джет вдоль магнитной оси |
Эти объекты включают в себя горячую вырожденную звезду с сильным магнитным полем, из фотосферы которой под действием давления циклотронного излучения истекает плазменный ветер, плотный плазменный диск вблизи магнитного экватора и пару струй-джетов, расположенных вдоль магнитной оси. Диск формируется истекающим веществом и поддерживается давлением излучения фотосферы. Возможность существования дисков околозвездных объектов хорошо известна в астрофизике. Такие диски образуются, например, в двойных системах при аккреции вещества с нормальной звезды на компактный объект. Другим примером служат молодые звезды, на стадии формирования которых диски могут возникать из газовых комплексов вследствие вращения системы. Радиационный дискон - пример особого астрофизического объекта с дисковой структурой, для существования которой не требуется вращения или аккреции со звезды-компаньона в двойной системе.
Как стать дисконом
Выясним прежде всего, при каких условиях магнитная вырожденная звезда (например, белый карлик) может стать радиационным дисконом.
Сердце дискона - центральная звезда. Она является источником вещества для формирования оболочки этого объекта и излучения, которое это вещество выбрасывает с поверхности звезды и поддерживает в магнитосфере. Дискон может сформироваться лишь в том случае, когда давление циклотронного излучения нарушает гидростатическое равновесие фотосферы. При каких параметрах звезды (величине температуры фотосферы и напряженности магнитного поля звезды) это возможно?
Сила давления циклотронного излучения пропорциональна потоку излучения на гирочастоте. Поэтому температура звезды должна быть достаточно высока, чтобы сила давления излучения, приходящаяся на одну частицу, превосходила силу тяжести mpg, действующую на протон (mp - масса протона, g - ускорение свободного падения на поверхности звезды). Очевидно, наиболее благоприятные условия для формирования дискона возникают в том случае, если гирочастота располагается вблизи максимума частотного спектра излучения звезды. Спектр излучения белого карлика в основном совпадает со спектром излучения абсолютно черного тела с той же температурой: спектральная интенсивность излучения на выходе из фотосферы одинакова во всех направлениях и составляет
![]()
где T* - температура поверхности звезды, ![]() - циклическая частота, h - постоянная Планка, k - постоянная Больцмана. Максимум этой функции соответствует частоте, для которой
- циклическая частота, h - постоянная Планка, k - постоянная Больцмана. Максимум этой функции соответствует частоте, для которой ![]() 2,82. Поэтому магнитное поле и температура звезды должны быть близки к значениям, при которых
2,82. Поэтому магнитное поле и температура звезды должны быть близки к значениям, при которых ![]() . Последнее соотношение можно представить в виде
. Последнее соотношение можно представить в виде
![]()
Лишь в этом случае может начаться истечение водородной плазмы из фотосферы. Конкретные расчеты, проведенные в работе [2], позволили построить диаграмму, показанную на рис. 2.
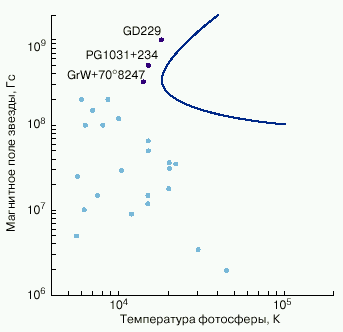 |
| Рис. 2. Диаграмма магнитное поле - температура фотосферы для белого карлика с ускорением свободного падения на поверхности g = 108 см/с2. Справа от сплошной кривой сила давления циклотронного излучения превышает силу тяжести. Светлыми точками показано положение на этой диаграмме известных магнитных белых карликов. Темными точками указаны звезды - кандидаты в радиационные дисконы |
Здесь в плоскости параметров lg B-lg T* проведена кривая, соответствующая значениям температуры и магнитного поля, при которых радиационная сила равна силе тяжести на поверхности белого карлика с g = 108 см/с2. При меньших температурах, слева от этой кривой, преобладает тяготение и вещество фотосферы находится в гидростатическом равновесии. Наоборот, при больших температурах, в области справа от кривой, равновесие фотосферы невозможно, поскольку в верхних ее слоях сила давления излучения превышает mpg. Из диаграммы видно, что наименьшая температура, при которой может начаться истечение вещества из фотосферы магнитного белого карлика, составляет около 2![]() 104 К; магнитное поле звезды при этом должно быть равно (3-6)
104 К; магнитное поле звезды при этом должно быть равно (3-6) ![]() 108 Гс, что в целом согласуется с приведенной выше оценкой благоприятной величины магнитного поля B. На диаграмме показаны также точки, соответствующие параметрам известных белых карликов. Темными точками отмечены три звезды с наиболее сильным магнитным полем: GD229, PG1031+234 и GrW+70°8247. Они имеют и довольно высокую температуру, так что эти объекты вполне могут стать кандидатами в радиационные дисконы.
108 Гс, что в целом согласуется с приведенной выше оценкой благоприятной величины магнитного поля B. На диаграмме показаны также точки, соответствующие параметрам известных белых карликов. Темными точками отмечены три звезды с наиболее сильным магнитным полем: GD229, PG1031+234 и GrW+70°8247. Они имеют и довольно высокую температуру, так что эти объекты вполне могут стать кандидатами в радиационные дисконы.
Сильно ли дует звездный ветер
Оценим поток вещества, который может создаваться давлением циклотронного излучения вблизи поверхности звезды. Допустим, что вдоль силовых линий магнитного поля через единицу площади проходит в единицу времени J частиц, которые разгоняются от дозвуковой скорости в основании течения до больших сверхзвуковых скоростей ![]() на выходе из него. Максимальная скорость потери массы достигается, если рассматриваемый поток плазмы полностью отбирает импульс от излучения, с которым он может взаимодействовать. Циклотронный резонанс возникает между плазмой и излучением с частотой
на выходе из него. Максимальная скорость потери массы достигается, если рассматриваемый поток плазмы полностью отбирает импульс от излучения, с которым он может взаимодействовать. Циклотронный резонанс возникает между плазмой и излучением с частотой ![]() в системе отсчета, связанной с плазмой. В соответствии с формулой Доплера соответствующая частота излучения в системе отсчета, связанной со звездой, равна
в системе отсчета, связанной с плазмой. В соответствии с формулой Доплера соответствующая частота излучения в системе отсчета, связанной со звездой, равна ![]() . Следовательно, истекающее вещество, разгоняясь от скорости
. Следовательно, истекающее вещество, разгоняясь от скорости ![]() до
до ![]() , перехватывает весь импульс излучения в интервале частот шириной порядка
, перехватывает весь импульс излучения в интервале частот шириной порядка ![]() . Продольная (вдоль магнитного поля) компонента потока импульса излучения в этом частотном интервале , где
. Продольная (вдоль магнитного поля) компонента потока импульса излучения в этом частотном интервале , где ![]() - угол между магнитным полем и радиусом-вектором, проведенным из центра звезды, а индекс * здесь и далее обозначает соответствующие величины на поверхности звезды. Приравнивая эту величину потоку импульса плазмы
- угол между магнитным полем и радиусом-вектором, проведенным из центра звезды, а индекс * здесь и далее обозначает соответствующие величины на поверхности звезды. Приравнивая эту величину потоку импульса плазмы ![]() , находим [4]
, находим [4]
![]()
(![]() - угол между магнитной осью звезды и радиусом-вектором). Интегрируя
- угол между магнитной осью звезды и радиусом-вектором). Интегрируя ![]() по звезде, определяем максимальную величину потери массы в единицу времени, обусловленную давлением циклотронного излучения:
по звезде, определяем максимальную величину потери массы в единицу времени, обусловленную давлением циклотронного излучения:
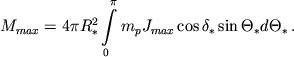
Оценки [3] , [4] показывают, что магнитный белый карлик с температурой 2 ![]() 104 К и полем (5-10)
104 К и полем (5-10) ![]() 108 Гс может терять около 20 000 т вещества в секунду, что составляет примерно 1% от темпа потери массы Солнца. Это большая величина, если учесть, что площадь белого карлика составляет всего лишь 10-4 от площади солнечной поверхности. Основная часть выброшенного вещества накапливается в закрытой части магнитосферы.
108 Гс может терять около 20 000 т вещества в секунду, что составляет примерно 1% от темпа потери массы Солнца. Это большая величина, если учесть, что площадь белого карлика составляет всего лишь 10-4 от площади солнечной поверхности. Основная часть выброшенного вещества накапливается в закрытой части магнитосферы.
Как устроена магнитосфера дискона
Рассмотрим более подробно строение плазменной магнитосферы дискона. Предположим сначала, что плазма вокруг звезды, обладающей дипольным магнитным полем, достаточно разрежена и излучение проходит через нее практически без ослабления (так называемый случай оптически тонкой магнитосферы). В этом случае можно пренебречь влиянием плазмы на излучение и считать интенсивность (а следовательно, и силу давления излучения) в любой точке вокруг звезды заданной и не зависящей от параметров плазменной оболочки. Анализ движения и плазмы в этом случае значительно упрощается.
Сила давления циклотронного излучения в оптически тонкой плазме вокруг звезды меняется с расстоянием r от центра звезды вследствие двух факторов. Во-первых, из-за сферической расходимости излучения его поток падает пропорционально (R* / r)2, где R* - радиус звезды. Во-вторых, более существенное влияние на силу давления циклотронного излучения оказывает неоднородность дипольного магнитного поля, вследствие которой гирочастота уменьшается с расстоянием от звезды: ![]() . Соответственно меняется и интенсивность излучения
. Соответственно меняется и интенсивность излучения ![]() , попадающего в резонанс с частицами магнитосферной плазмы. Рано или поздно гирочастота смещается в низкочастотную часть спектра
, попадающего в резонанс с частицами магнитосферной плазмы. Рано или поздно гирочастота смещается в низкочастотную часть спектра ![]() , где зависимость интенсивности от частоты описывается законом Рэлея-Джинса; в этом случае
, где зависимость интенсивности от частоты описывается законом Рэлея-Джинса; в этом случае ![]() . Поэтому, пройдя через точку максимума, сила давления излучения
. Поэтому, пройдя через точку максимума, сила давления излучения ![]() начинает уменьшаться гораздо быстрее, чем сила тяжести
начинает уменьшаться гораздо быстрее, чем сила тяжести ![]() . Следовательно, даже если вблизи звезды давление излучения намного превышает силу тяжести, на некотором расстоянии r0 эти силы сравняются, а потом тяготение окажется превалирующим. Поэтому вокруг звезды существует равновесная поверхность, на которой компоненты силы давления излучения и силы тяжести вдоль магнитного поля компенсируют друг друга:
. Следовательно, даже если вблизи звезды давление излучения намного превышает силу тяжести, на некотором расстоянии r0 эти силы сравняются, а потом тяготение окажется превалирующим. Поэтому вокруг звезды существует равновесная поверхность, на которой компоненты силы давления излучения и силы тяжести вдоль магнитного поля компенсируют друг друга:![]() . Решая это уравнение, можно определить форму равновесной поверхности - зависимость
. Решая это уравнение, можно определить форму равновесной поверхности - зависимость ![]() . Результаты расчетов [3],[4] приведены на рис. 3.
. Результаты расчетов [3],[4] приведены на рис. 3.
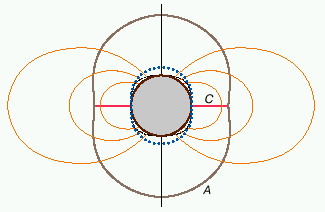 |
| Рис. 3. Структура плазменной оболочки радиационного дискона [3], [4], [5]. Оптически тонкая плазма концентрируется вблизи замкнутой равновесной поверхности А, охватывающей звезду, и диска С в плоскости магнитного экватора. Оптически толстая плазменная оболочка простирается от звезды до равновесной поверхности. Циклотронное рассеяние в такой оболочке приводит к формированию широкой и глубокой полосы депрессии в спектре наблюдаемого излучения дискона. Точками показан гирорезонансный слой, соответствующий коротковолновому краю полосы |
Для реальных параметров магнитных белых карликов равновесная поверхность отстоит от поверхности звезды примерно на (1-2)R*.
Итак, циклотронное излучение может поддерживать плазму вокруг магнитной звезды лишь в довольно компактной области. Выясним, как распределяется в ней "выметенное" с поверхности звезды вещество. Гидростатическое равновесие вдоль магнитного поля определяется балансом сил тяжести, давления плазмы и давления излучения
![]()
В этом уравнении введена координата h вдоль силовой линии, использовано выражение p = 2NkT для давления полностью ионизованной водородной плазмы (T и N - ее температура и концентрация, совпадающая с концентрациями электронов и протонов), а также учтено, что из-за весьма большой теплопроводности горячей плазмы температура T (при отсутствии притока или отвода тепла) будет практически одинакова во всех точках вдоль силовой линии.
Определим точки максимума плотности плазмы, в которых dN / dl = 0. Это, во-первых, равновесная поверхность r0(Q) и, кроме того, часть плоскости магнитного экватора (Q = p /2), заключенная между звездой и равновесной поверхностью. Действительно, в этом месте продольные (вдоль магнитного поля) компоненты сил тяжести и радиационного давления обращаются в нуль, что и обеспечивает соблюдение равенства dN / dl = 0.
Отметим, что для силовых линий, пересекающих равновесную поверхность, продольная компонента радиационной силы превышает соответствующую проекцию силы тяжести в области между звездой и равновесной поверхностью, так что их равнодействующая направлена к вершине силовой линии. Наоборот, вне равновесной поверхности, где доминирует сила тяжести, продольная компонента равнодействующей направлена к поверхности звезды. Для тех силовых линий, которые расположены целиком под равновесной поверхностью, рассматриваемая проекция равнодействующей направлена к плоскости магнитного экватора, на которой она обращается в нуль. Следовательно, сама равновесная поверхность и часть плоскости магнитного экватора, заключенная внутри нее, представляют собой области устойчивого равновесия - потенциальную яму для плазмы: при смещении частицы из этой области вдоль силовой линии возникает возвращающая сила. Вблизи равновесной поверхности и заключенной внутри нее части магнитного экватора будет накапливаться плазма. Распределение плазмы в потенциальной яме вблизи равновесной поверхности имеет вид
![]()
где ![]() , N0 - концентрация плазмы на равновесной поверхности,
, N0 - концентрация плазмы на равновесной поверхности, ![]() - характерная толщина оболочки, выраженная в радиусах звезды,
- характерная толщина оболочки, выраженная в радиусах звезды,
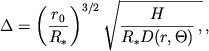
H = 2kT / (mp g), а D (r,![]() ) - медленно меняющаяся функция порядка единицы, вид которой не приводится из-за громоздкости. Так как H
) - медленно меняющаяся функция порядка единицы, вид которой не приводится из-за громоздкости. Так как H ![]() R* , то толщина рассматриваемой оболочки составляет лишь несколько процентов от величины r0 . Полное количество вещества, накапливающегося в такой оболочке, можно оценить интегрируя распределение
R* , то толщина рассматриваемой оболочки составляет лишь несколько процентов от величины r0 . Полное количество вещества, накапливающегося в такой оболочке, можно оценить интегрируя распределение ![]() :
:
![]()
Если ничто не препятствует накоплению вещества в магнитосфере, то за счет истечения плазмы с поверхности концентрация в оболочке будет расти. Постепенно оболочка станет настолько плотной, что уже нельзя будет пренебречь ее влиянием на распределение излучения вокруг звезды. Произойдет это в тот момент, когда размер оболочки станет сравним со средней длиной свободного пробега фотонов или, что то же самое, оптическая толщина плазмы на циклотронной частоте станет порядка единицы. Если это условие выполняется при некоторой концентрации ![]() , то минимальное время накопления оптически толстой оболочки примерно равно
, то минимальное время накопления оптически толстой оболочки примерно равно
![]()
Оценки, сделанные в [3] , [4] для типичных параметров белых карликов, показывают, что время t0 очень мало - порядка десятка секунд. Таким образом, тонкий "кокон" вблизи равновесной поверхности мог бы существовать лишь короткое время. После этого вокруг звезды накапливается достаточно плотная плазма, меняющая интенсивность излучения и пространственное распределение радиационного давления. В этом случае профиль концентрации вещества вокруг звезды формируется под действием давления излучения, которое, в свою очередь, этим веществом определяется.
Качественную картину строения оптически толстой оболочки можно представить определив характер движения плазмы вблизи равновесной поверхности в тот момент, когда ее оптическая толщина приближается к единице и она начинает ослаблять поток излучения и уменьшать силу радиационного давления. Равновесие силы тяжести и силы давления излучения нарушается, сила тяжести слегка превышает радиационную, и плазма "проседает" ближе к поверхности звезды. Там поток излучения на резонансной частоте больше, так что радиационная сила, даже ослабленная за счет рассеяния в оптически толстой плазме, может скомпенсировать тяготение. Далее поступающее от звезды вещество будет накапливаться еще ниже, и в конце концов вся область между звездой и равновесной поверхностью заполнится оптически толстой плазмой.
Равновесный профиль концентрации можно определить, если принять во внимание сильную неоднородность магнитного поля. Действительно, излучение на данной частоте попадает в циклотронный резонанс с плазмой, помещенной в неоднородное магнитное поле, лишь в ограниченной области пространства - гирорезонансном слое. Его размер можно оценить вспоминая, что тепловое движение электронов со скоростями ![]() приводит к доплеровскому разбросу резонансных частот
приводит к доплеровскому разбросу резонансных частот ![]() , который обычно существенно меньше
, который обычно существенно меньше ![]() (здесь
(здесь ![]() - угол между направлением распространения излучения и магнитным полем). Размер гирорезонансного слоя lB соответствует расстоянию, на котором гирочастота меняется на величину порядка ширины циклотронной линии:
- угол между направлением распространения излучения и магнитным полем). Размер гирорезонансного слоя lB соответствует расстоянию, на котором гирочастота меняется на величину порядка ширины циклотронной линии: ![]() , где l - координата вдоль направления распространения излучения. Считая циклотронную линию достаточно узкой, представим левую часть этого уравнения в виде
, где l - координата вдоль направления распространения излучения. Считая циклотронную линию достаточно узкой, представим левую часть этого уравнения в виде ![]() , отсюда находим, что
, отсюда находим, что
![]()
где ![]() - характерный масштаб неоднородности магнитного поля. Для плазмы в магнитосфере белого карлика с дипольным полем
- характерный масштаб неоднородности магнитного поля. Для плазмы в магнитосфере белого карлика с дипольным полем ![]() , а
, а ![]() 10^{-2}, так что для достаточно плавного распределения концентрации можно пренебречь неоднородностью N на масштабе порядка lB . Теперь выясним, каково предельное количество вещества, которое может поддерживаться излучением звезды в данной точке магнитосферы. Допустим, что плазма вокруг звезды достаточно плотная и весь импульс излучения, которое в состоянии взаимодействовать с веществом в рассматриваемой точке, передается плазме (именно в этом случае радиационная сила будет максимальна). Если вещество в гирорезонансном слое толщиной lB и единичной площадью взаимодействует с излучением из интервала частот
10^{-2}, так что для достаточно плавного распределения концентрации можно пренебречь неоднородностью N на масштабе порядка lB . Теперь выясним, каково предельное количество вещества, которое может поддерживаться излучением звезды в данной точке магнитосферы. Допустим, что плазма вокруг звезды достаточно плотная и весь импульс излучения, которое в состоянии взаимодействовать с веществом в рассматриваемой точке, передается плазме (именно в этом случае радиационная сила будет максимальна). Если вещество в гирорезонансном слое толщиной lB и единичной площадью взаимодействует с излучением из интервала частот ![]() вблизи
вблизи ![]() , то ему передается импульс
, то ему передается импульс ![]() в единицу времени. Возникающая при этом сила должна скомпенсировать силу тяжести mpg(r /R*)-2NlB , действующую на вещество в рассматриваемом объеме. Приравнивая силу тяжести и силу давления излучения, находим профиль концентрации плазмы
в единицу времени. Возникающая при этом сила должна скомпенсировать силу тяжести mpg(r /R*)-2NlB , действующую на вещество в рассматриваемом объеме. Приравнивая силу тяжести и силу давления излучения, находим профиль концентрации плазмы
![]()
Все пространство между звездой и равновесной поверхностью заполняется плазмой с таким распределением концентрации за время
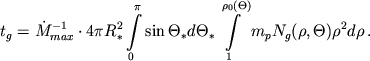
Дальнейшее накопление вещества за счет притока с поверхности звезды нарушит равновесие сил и приведет к разрушению оболочки. При этом магнитосфера "просветлится", сила давления излучения возрастет и начнется новый цикл накопления плазмы между звездой и равновесной поверхностью.
Как увидеть радиационный дискон
Анализ показывает, что вокруг горячих магнитных белых карликов с достаточно сильным магнитным полем возникает оптически толстая нестационарная плазменная оболочка, формируемая и поддерживаемая давлением излучения, идущего от звезды. Ясно, что такая плазменная структура должна заметно менять наблюдаемое излучение звезды. По характеру этих изменений и можно судить о существовании радиационных дисконов в Галактике.
В плазме, находящейся в магнитосфере белого карлика, могут распространяться электромагнитные волны двух типов: обыкновенная и необыкновенная [5]. Обе эти волны эллиптически поляризованы: конец вектора электрического поля описывает эллипс, подобный проекции ларморовской окружности электрона на плоскость, перпендикулярную направлению распространения волны (при распространении вдоль магнитного поля этот эллипс вырождается в окружность, а поперек - в отрезок). Необыкновенная волна поляризована так, что электрический вектор вращается в ту же сторону, что и электрон в магнитном поле. Для этой волны циклотронный резонанс проявляется наиболее сильно. В обыкновенной волне вращение вектора электрического поля противоположно вращению электрона, поэтому она взаимодействует с плазмой гораздо слабее. Циклотронный резонанс для обыкновенных волн в плазме на белых карликах практически отсутствует, в то время как сильное циклотронное рассеяние необыкновенного излучения в неоднородном магнитном поле делает его изотропным. Интенсивность рассеянного необыкновенного излучения, выходящего во все стороны из гирорезонансного слоя, составляет примерно половину того, что подходит к нему от поверхности звезды:![]() . Напротив, интенсивность обыкновенной компоненты практически не меняется:
. Напротив, интенсивность обыкновенной компоненты практически не меняется: ![]() . Следовательно, если звезда закрыта от наблюдателя оптически толстой плазменной оболочкой, в ее спектре на частотах
. Следовательно, если звезда закрыта от наблюдателя оптически толстой плазменной оболочкой, в ее спектре на частотах ![]() в интервале
в интервале ![]() возникнет дефицит излучения: его интенсивность составит лишь
возникнет дефицит излучения: его интенсивность составит лишь ![]() от уровня излучения фотосферы. Излучение в пределах указанного частотного интервала (полосы депрессии) должно быть сильно поляризовано, так как
от уровня излучения фотосферы. Излучение в пределах указанного частотного интервала (полосы депрессии) должно быть сильно поляризовано, так как ![]() . Наконец, любые вариации плотности плазмы вокруг звезды должны проявляться в виде переменности интенсивности излучения и степени его поляризации в полосе депрессии. Перечисленные характерные черты довольно легко обнаружить, что делает поиск дисконов отнюдь не безнадежным делом.
. Наконец, любые вариации плотности плазмы вокруг звезды должны проявляться в виде переменности интенсивности излучения и степени его поляризации в полосе депрессии. Перечисленные характерные черты довольно легко обнаружить, что делает поиск дисконов отнюдь не безнадежным делом.
Наиболее вероятным кандидатом в радиационные дисконы является магнитный белый карлик GD229 - самый необычный представитель этой небольшой группы звезд. Его излучение в непрерывном спектре сильно поляризовано: степень линейной поляризации оптического континуума составляет около 4%, что косвенным образом указывает на наличие сильного магнитного поля. Помимо этого GD229 имеет исключительно богатый спектр, содержащий множество особенностей в поглощении (рис. 4).
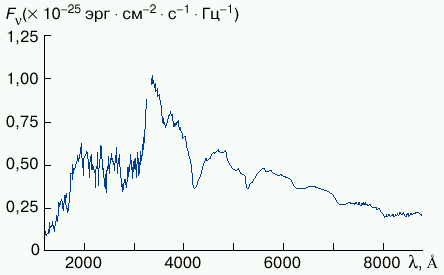 |
| Рис. 4. Спектр магнитного белого карлика GD229 от инфракрасного до ультрафиолетового диапазона [6]. Видны многочисленные спектральные особенности в оптическом диапазоне и сильнейшая полоса депрессии в ближнем ультрафиолетовом диапазоне на длинах волн 2000-3000 A |
Неоднократные попытки интерпретировать всю совокупность наблюдаемых линий и полос успеха пока не имели, так что уже более 15 лет спектр звезды остается необъясненным. Однако его наиболее заметную деталь - чрезвычайно широкую и глубокую полосу поглощения в ближнем ультрафиолетовом диапазоне на длинах волн 2000-3000 A - можно объяснить циклотронным рассеянием в плазменной оболочке, находящейся в неоднородном магнитном поле вокруг звезды и закрывающей от наблюдателя весь ее диск. Альтернативное объяснение, что такая спектральная особенность обязана своим происхождением какому-либо атомному переходу, модифицированному в сильном магнитном поле, кажется весьма маловероятным.
О магнитном поле звезды в случае циклотронного происхождения можно судить по положению этой полосы в спектре. Считая, что коротковолновый край депрессии соответствует магнитному полю вблизи экватора белого карлика, получим оценку величины этого поля 5 ![]() 108 Гс (соответственно поле на магнитном полюсе Bp
108 Гс (соответственно поле на магнитном полюсе Bp ![]() 109 Гс). Форма спектра вне полосы депрессии соответствует излучению черного тела с температурой T*
109 Гс). Форма спектра вне полосы депрессии соответствует излучению черного тела с температурой T* ![]() (1,8-2)
(1,8-2) ![]() 104 К. Согласно диаграмме на рис. 2, существование стационарной фотосферы при этом невозможно, и должен возникать ветер, порождаемый излучением на циклотронных частотах. При этом с поверхности звезды может истекать около 20 000 т вещества в секунду. Равновесная поверхность, на которой сравниваются продольные компоненты силы тяжести и силы давления излучения, в рассматриваемом случае отстоит от поверхности звезды примерно на 3R* в направлении магнитной оси и на 2,2R* в плоскости магнитного экватора. При указанном темпе потери массы пространство между звездой и этой равновесной поверхностью заполняется оптически толстой плазмой за время порядка одного часа.
104 К. Согласно диаграмме на рис. 2, существование стационарной фотосферы при этом невозможно, и должен возникать ветер, порождаемый излучением на циклотронных частотах. При этом с поверхности звезды может истекать около 20 000 т вещества в секунду. Равновесная поверхность, на которой сравниваются продольные компоненты силы тяжести и силы давления излучения, в рассматриваемом случае отстоит от поверхности звезды примерно на 3R* в направлении магнитной оси и на 2,2R* в плоскости магнитного экватора. При указанном темпе потери массы пространство между звездой и этой равновесной поверхностью заполняется оптически толстой плазмой за время порядка одного часа.
Циклотронное рассеяние излучения звезды в этой плазменной оболочке может привести к возникновению широкой полосы депрессии на уровне 75% от уровня континуума. Это первое следствие, к которому приводит модель радиационного дискона. Его можно проверить пользуясь известными наблюдательными данным. Рисунок 5 показывает, что интенсивность в полосе депрессии в спектре GD229 действительно близка к значению, указываемому теорией.
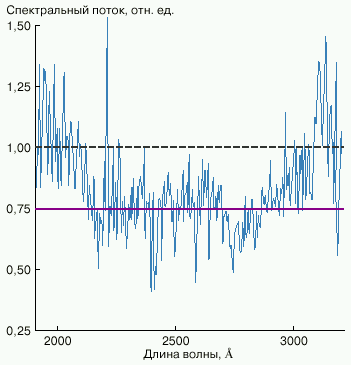 |
| Рис. 5. Спектр GD229 в ближнем ультрафиолетовом диапазоне, полученный спутником IUE 23 января 1980 года во время сеанса наблюдений длительностью 60 мин [7]. По вертикальной оси отложено отношение спектрального потока излучения звезды к спектральному потоку излучения абсолютно черного тела с температурой 1,8 |
Вторым важным предсказанием в модели дискона является сильная поляризация излучения в полосе депрессии, которая может достигать десятков процентов. К сожалению, нам не удалось получить какие-либо данные о поляриметрических наблюдениях GD229 в ультрафиолетовом диапазоне и проверить это предсказание теории мы не смогли. Наконец, третье интересное следствие существования вокруг GD229 нестационарной плазменной атмосферы, поддерживаемой циклотронным излучением, - переменность излучения в полосе депрессии с характерными временами около 1 часа. Наблюдательные данные дают некоторые указания на подобную переменность. На рис. 6 представлены ультрафиолетовые спектры GD229, полученные в январе 1980 года. Время накопления спектров составляло от 60 до 90 минут. Чтобы снизить влияние посторонних шумов, мы усреднили наблюдательные данные по длинам волн. Графики показывают, что изменение уровня излучения в полосе депрессии статистически значимо. Конечно, это лишь предварительный результат. С большей уверенностью говорить о том, что GD229 - радиационный дискон, можно будет после проведения дополнительных спектральных и поляризационных наблюдений.
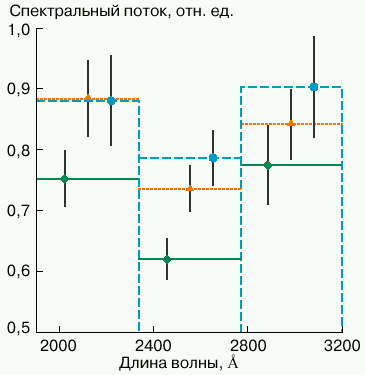 |
| Рис. 6. Указания на переменность излучения в полосе депрессии в спектре GD229. Гистограммы показывают среднюю интенсивность излучения в соответствующих интервалах длин волн для трех наблюдений длительностью 80 мин (зеленая линия), 60 мин (голубая линия) и 90 мин (оранжевая линия), выполненных в январе 1980 года спутником IUE. Единицы измерения по вертикальной оси такие же, как на рис. 5. Штрихи у точек соответствуют трем стандартным отклонениям s от указанного среднего значения. Один из спектров на длинах волн 1900-2760 A отличается от других более чем на 3 |
Интересно отметить, что в спектре другого кандидата в радиационные дисконы - белого карлика PG1031+234 также имеется указание на наличие полосы депрессии в ультрафиолетовом диапазоне, куда попадает гирочастота, соответствующая магнитному полю этой звезды B ![]() (0,5-1)
(0,5-1) ![]() 109 Гс. Действительно, согласно рис. 7, спектр PG1031+234 в инфракрасном и видимом диапазонах хорошо соответствует температуре T*
109 Гс. Действительно, согласно рис. 7, спектр PG1031+234 в инфракрасном и видимом диапазонах хорошо соответствует температуре T* ![]() 2,5
2,5 ![]() 104 К, в то время как в ультрафиолетовой части спектра интенсивность наблюдаемого излучения значительно меньше. По нашему мнению, это свидетельствует о наличии широкой полосы депрессии, которая формируется точно так же, как на GD229. Подтвердить эту гипотезу могли бы наблюдения поляризации и временной переменности ультрафиолетового излучения PG1031+234.
104 К, в то время как в ультрафиолетовой части спектра интенсивность наблюдаемого излучения значительно меньше. По нашему мнению, это свидетельствует о наличии широкой полосы депрессии, которая формируется точно так же, как на GD229. Подтвердить эту гипотезу могли бы наблюдения поляризации и временной переменности ультрафиолетового излучения PG1031+234.
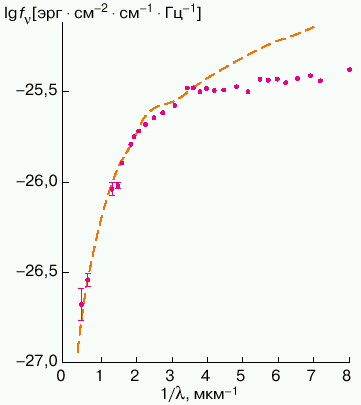 |
| Рис. 7. Спектральный поток fn наблюдаемого излучения магнитного белого карлика PG1031+234; |
Объекты, подобные описанному в статье радиационному дискону, требуют для своего существования лишь достаточно высокой температуры поверхности звезды и сильного магнитного поля. В этом смысле модель радиационного дискона универсальна. Помимо магнитных белых карликов плазменный ветер и оболочки, порождаемые давлением излучения на циклотронных частотах, могут наблюдаться у центральных звезд планетарных туманностей - эволюционных предшественников белых карликов, которые имеют температуру T* ![]() 105 К (конечно, при условии, что магнитное поле этих звезд превышает 108 Гс), а также у одиночных нейтронных звезд с B
105 К (конечно, при условии, что магнитное поле этих звезд превышает 108 Гс), а также у одиночных нейтронных звезд с B ![]() (0,2-1)
(0,2-1) ![]() 1011 Гс и T*
1011 Гс и T* ![]() (2-4)
(2-4) ![]() 106 К. У нейтронных звезд с параметрами B
106 К. У нейтронных звезд с параметрами B ![]() 1010 Гс и T*
1010 Гс и T* ![]() (1-3)
(1-3) ![]() 107 К, которые входят в состав маломассивных рентгеновских двойных систем, дисконы могут формироваться спорадически во время рентгеновских всплесков, а в спокойном состоянии радиационное давление может менять темп аккреции и порождать квазипериодические осцилляции наблюдаемого рентгеновского излучения. Развитие теории радиационных дисконов применительно к этим объектам - дело ближайшего будущего.
107 К, которые входят в состав маломассивных рентгеновских двойных систем, дисконы могут формироваться спорадически во время рентгеновских всплесков, а в спокойном состоянии радиационное давление может менять темп аккреции и порождать квазипериодические осцилляции наблюдаемого рентгеновского излучения. Развитие теории радиационных дисконов применительно к этим объектам - дело ближайшего будущего.
Литература
| [1] | Беспалов П.А., Железняков В.В. // Письма в "Астрон. журн." 1990. Т. 16. С. 1030. |
| [2] | Железняков В.В., Сербер А.В. // Там же. 1991. Т. 17. С. 419. |
| [3] | Zheleznyakov V.V., Serber A.V. // Space Sci. Rev. 1994. Vol. 68. P. 275. |
| [4] | Zheleznyakov V.V., Serber A.V., Kuijpers J. // Astron. Astrophys. 1996. Vol. 308. P. 465. |
| [5] | Zheleznyakov V.V. Radiation in Astrophysical Plasmas. Kluwer Acad. Publ., 1996 |
| [6] | Schmidt G.D., Latter W.B., Foltz C.B. // Astrophys. J. 1990. Vol. 350. P. 758. |
| [7] | Green R.F., Liebert J. // Publ. Astron. Soc. Pacific. 1981. Vol. 93. P. 105. |
| [8] | Schmidt G.D., West S.C., Liebert J. et al. // Astrophys. J. 1986. Vol. 309. P. 318. |
|
Публикации с ключевыми словами:
истечение вещества - нейтронные звезды - давление излучения - сильное магнитное поле - циклотронное излучение - Плазма - белый карлик
Публикации со словами: истечение вещества - нейтронные звезды - давление излучения - сильное магнитное поле - циклотронное излучение - Плазма - белый карлик | |
См. также:
Все публикации на ту же тему >> | |