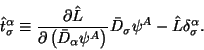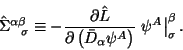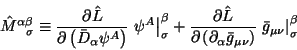- 2.1.1 Проблемы определения углового момента в полевой теории
- 2.1.2 Симметризация Белинфанте
- 2.1.3 Теорема Нетер и метод Белинфанте
2.1 Классический метод Белинфанте
2.1.1 Проблемы определения углового момента в полевой теории
Вначале мы коротко изложим основные положения
оригинальной работы Белинфанте [1], во многом даже следуя его стилю и
обозначениям. Рассмотрим теорию некоторых динамических
полей представленных обобщенным символом ![]() с лагранжианом
с лагранжианом
и сохраняется
на выполненных уравнениях движения. Следуя правилам обычной механики тензорную плотность углового (орбитального) момента следоволо бы определить как
Здесь возникает проблема: определенный таким образом угловой момент не сохраняется
даже с учетом закона сохранения (2.3). Дело в том, что тензор энергии-импульса определенный в (2.2) в общем случае не симметричен. Ситуацию в (2.5) мог бы спасти сохраняющийся симметричный тензор энергии-импульса, который можно было бы построить по другим правилам, или симметризовать уже имеющийся (2.2).
2.1.2 Симметризация Белинфанте
Вторую из этих возможностей использовал Белинфанте [1],
который предложил следующее.
Пусть при бесконечно малых вращениях
определяемых антисимметричным параметром
![]() вариации координат и динамических переменных имеют вид:
вариации координат и динамических переменных имеют вид:
![]() и
и
![]() ,
где
,
где
![]() -- оператор.
Определим величину
-- оператор.
Определим величину
Далее величину (2.6) или ее обобщения мы будем называть поправкой Белинфанте. Теперь добавим производную от (2.6) к каноническому выражению (2.2):
Как и прежде, в (2.3):
сохраняется
2.1.3 Теорема Нетер и метод Белинфанте
В оригинальном изложении метод Белинфанте
представлен, фактичести, на уровне уравнений движения.
Сейчас мы опишем его единым образом в рамках
лагранжевой теории.
Для этого запишем лагранжиан (2.1) в общековариантном виде:
с определенной как в лекции 1 производной Ли:
и произвольным вектором
Структура этого тока важна и мы ее обсудим подробно. Первый член -- это симметричный (так называемый метрический) тензор энергии-импульса полей
второе слагаемое выражено уже известным каноническим тензором энергии-импульса (2.2), только теперь мы записываем его в явно ковариантном виде:
В третьем слагаемом в (2.11) главную роль играет спиновый тензор:
Мы предполагаем, что уравнения движения
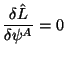 |
выполняются и не будем больше учитывать предпоследний член в (2.11). Наконец, структуру Z-члена мы не выписываем, но отмечаем, что он исчезает на киллинговых векторах фона.
В силу тождества
![]() должен существовать суперпотенциал, то есть антисимметричная
тензорная плотность. Действительно, такой суперпотенциал существует,
и закон сохранения
должен существовать суперпотенциал, то есть антисимметричная
тензорная плотность. Действительно, такой суперпотенциал существует,
и закон сохранения
![]() может быть заменен
законом сохранения:
может быть заменен
законом сохранения:
антисимметрична по верхним индексам:
Сравнивая определения (2.7) и (2.14)
мы определяем поправку
Белинфанте точно также как в (2.6):
и добавим к обеим частям
В силу определения (2.17) спиновый член в левой части (2.18) компенсируется добавкой Белинфанте. Кроме того, оказывается, что выражения в формулах (2.16) и (2.17) совпадают в общем случае:
Теперь запишем симметризованный с помощью метода Белинфанте, как это было сделано в (2.8), канонический тензор энергии-импульса:
Сравнивая последние два равенства находим, что симметризованный тензор энергии-импульса (2.19) равен метрическому тензору энергии-импульса (2.12):
![]() .
.
Электординамика,
лагранжиан которой соответствует форме (2.9),
является хорошей иллюстрацией изложенного. Канонический тензор энергии- импульса (2.13) и тензор спина (2.14) преобретают вид:
| = | 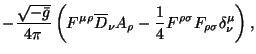 |
||
| = | ![$\displaystyle -{\sqrt{-\bar g}\over 4\pi}F^{\mu[\rho}A^{\sigma]}.$](http://images.astronet.ru/pubd/2001/09/12/0001170672/img197.gif) |
Тогда поправка Белинфанте (2.17) записывается как
![$\displaystyle \hat S^{\dag\mu\nu\rho}=
\hat \Sigma^{\dag\rho[\mu\nu]}+
\hat \Si...
...-
\hat \Sigma^{\dag\nu[\rho\mu]}= {\sqrt{-\bar g}\over 4\pi} F^{\mu\nu}A^{\rho}$](http://images.astronet.ru/pubd/2001/09/12/0001170672/img198.gif) |
и приводит к Белинфанте модифицированному тензору энергии-импульса (2.19):
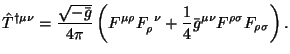 |
С другой стороны, это есть известный симметричный, калибровочно инвариантный тензор энергии-импульса электоромагнитного поля, который получается варьированием
<< 2. Развитие и обобщение ... | Оглавление | 2.2 Приложение процедуры Белинфанте ... >>
|
Публикации с ключевыми словами:
законы сохранения - Общая теория относительности - гравитация
Публикации со словами: законы сохранения - Общая теория относительности - гравитация | |
См. также:
Все публикации на ту же тему >> | |
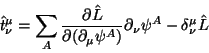
![\begin{displaymath}
\hat f_{\mu\nu}^{??\alpha} \equiv
\sum_A {{\partial \hat L}\...
... {\partial(\partial_\alpha \psi^A)}}{\bf S}_{[\mu\nu]}
\psi^A.
\end{displaymath}](http://images.astronet.ru/pubd/2001/09/12/0001170672/img164.gif)