<< 1.7 Вариационный принцип | Оглавление | 2. Аналитическая теория политропных ... >>
1.8 Теорема вириала
Предположим, что уравнение состояния степенное:
![]() . Тогда удельная
тепловая энергия
. Тогда удельная
тепловая энергия
![]() . Мы знаем, что в равновесии
. Мы знаем, что в равновесии
![]() при произвольной
при произвольной
![]() . Пусть
. Пусть
![]() .
Такое возмущение
описывает подобное (гомологическое) расширение или сжатие звезды. Тогда
.
Такое возмущение
описывает подобное (гомологическое) расширение или сжатие звезды. Тогда
![]() . Следовательно,
. Следовательно,
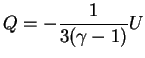
Теперь положим
![]() , причем не будем считать
, причем не будем считать ![]() малой величиной,
а исходное состояние -- равновесным. Обозначим через
малой величиной,
а исходное состояние -- равновесным. Обозначим через ![]() и
и ![]() соответствующие
величины энергий исходной модели. Тогда после преобразования
соответствующие
величины энергий исходной модели. Тогда после преобразования
![]() (для степенного уравнения состояния). Если
(для степенного уравнения состояния). Если
![]() , то
, то
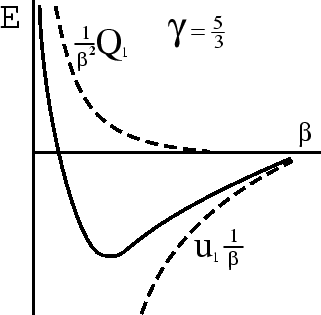
![]() . Как выглядит в этом случае
кривая
. Как выглядит в этом случае
кривая
![]() ? При
? При
![]() асимптотика определяется
величиной
асимптотика определяется
величиной ![]() , при
, при
![]() -- величиной
-- величиной ![]() (рис. 11). Получаем, что при
(рис. 11). Получаем, что при
![]() кривая имеет один и только один минимум, т.е. равновесие устойчиво.
кривая имеет один и только один минимум, т.е. равновесие устойчиво.
Получим теорему вириала другим способом из уравнения равновесия, причем зависимость
![]() может быть произвольной. (Выше при выводе теоремы вириала из вариационного
принципа зависимость
может быть произвольной. (Выше при выводе теоремы вириала из вариационного
принципа зависимость
![]() была существенна). Умножим уравнение равновесия
(1.6) на
была существенна). Умножим уравнение равновесия
(1.6) на ![]() :
:
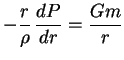
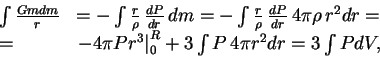
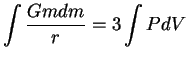
При степенном уравнении состояния, используя
![]() , имеем уже
известное соотношение
, имеем уже
известное соотношение
![]() .
.
В действительности уравнение состояния не степенное, но для многих оценок полезно
знать свойства звезд с таким уравнением состояния. Для степенного уравнения
состояния имеется подобие, т.е. достаточно решить задачу при данном ![]() для одного значения
для одного значения ![]() , чтобы найти функциональную зависимость
, чтобы найти функциональную зависимость ![]() и
и ![]() . В систему уравнений
. В систему уравнений
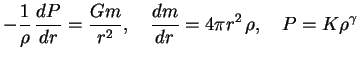
![$\displaystyle [G]={\mbox{см}^3\over \mbox{г} \cdot \mbox{с}^2}, \;[K]={\mbox{см...
...\over \mbox{см}^3}\right)^{-\gamma+1}, \;[\rho_c]=
{\mbox{г}\over\mbox{см}^3}.
$](http://images.astronet.ru/pubd/2008/02/15/0001226214/img305.gif)
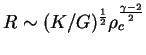 .
.
Более наглядно эта связь получается с помощью порядковых оценок:
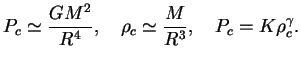
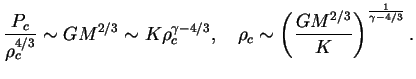
Подчеркнем, что вид кривых ![]() и
и ![]() зависит от безразмерной
величины
зависит от безразмерной
величины ![]() , т.е. кривые для разных
, т.е. кривые для разных ![]() не подобны.
не подобны.
<< 1.7 Вариационный принцип | Оглавление | 2. Аналитическая теория политропных ... >>
|
Публикации с ключевыми словами:
Эволюция звезд - внутреннее строение звезд - термоядерные реакции - физические процессы
Публикации со словами: Эволюция звезд - внутреннее строение звезд - термоядерные реакции - физические процессы | |
См. также:
Все публикации на ту же тему >> | |