args[0]=message
args[1]=DB::DB::Message=HASH(0x399ebc0)
Re: Черная дыра
29.06.2014 14:07 | А.П. Васи
 Физические котлеты и математические мухи.
Физические котлеты и математические мухи.Вчера :: 18:10:57
http://www.sciteclibrary.ru/cgi-bin/yabb2/YaBB.pl?num=1403964657
\\\По этой причине, чтобы не остаться голодными и не питаться математическими
моделями котлет нужно уметь отделять математических мух от физических котлет.
К сожалению, на сегодняшний день, всё это настолько перепутано, что вместо
реальных физических котлет нам приходится питаться паштетом из математических
моделей.
Типичным примером такого подлога является теория относительности, когда вместо
реальной физической модели нам подсунули математический суррогат и заставляют
его есть. А он нам просто не лезет.
С некоторых пор, математики окончательно разбушевавшись, как это умел делать
Фантомас, математика начала изобретать свои физические законы, и это касается не
только ТО. Нам начали подсовывать суррогат из зависящей от частоты диэлектрической
проницаемости плазмы и частотозависимой диэлектрической проницаемости
диэлектриков, предлагая на этой почве построить вечные двигатели. Начали нас
кормить волновыми функциями и квантами электромагнитного поля.
Вобщем, вся современная физика это сплошной неудобоваримый метафизический
суррогат из практически несъедобных математических моделей.
Но где же подевались настоящие котлеты из натурального физического мяса.
А их украли у нас Эйнштейны, Ландау и Гизбурги и иже с ними, и вместе с ними украли
у нас и всю физику.\\\
------------------------------------------------------------------------------------------
С моей точки зрения физику украсть у физика невозможно, лично мне в
этом контексте сложившейся ситуации в физике сто лет назад и продолжающуюся
до сих пор - очень обидно за мои школьные годы, и за ту физику которую мне
преподавали по школьным учебникам, за то что на самом деле
есть книжки по физике и по лучше раз в 30, а если их бы альты переписали
то они бы были вообще хорошие - я даже уверен что такого не произойдёт.
Собственно без адекватной базовой физики в школьные годы, юзер
не получает адекватных знаний о практических достижениях и не знает
уже проведенных опытах, и будет вынужден всю эту ботву изучать
с нуля и вникать в неё по картинкам и описаниям через интернет.
Что собственно и есть базовый тормоз.
И вообще если на сегодняшний день нет физического определения
сопротивления проводника - то это ясный конь - позор, но
это надо осознать сперва, потом поставить такую задачу,
потом про-финансировать конкурс на лучшие модели.
Потом выбрать - а вот здесь я задам вопрос на который каждый
может сам себе ответить самостоятельно -
Выберут ту модель -
- Автор которой пообещает больше из премии комиссии
- которая лучше описывает физический смысл в механическом варианте,
- которая содержит больше формул,
- которая меньше всего противоречит текущей парадигме
- автор которой имеет звание академика
- автор которой член комиссии по борьбе с лженаукой
?
[Цитировать][Ответить][Новое сообщение]
| Форумы >> Обсуждение публикаций Астронета |
| Список / Дерево Заголовки / Аннотации / Текст |
- Черная дыра
(И. Д. Новиков, "Физика Космоса", 1986,
26.03.2003 20:16, 22.4 КБайт, ответов: 659)
1. Введение
2. Поле тяготения невращающейся черной дыры
3. Поле тяготения вращающейся черной дыры
4. Физические процессы в поле тяготения черной дыры1. Введение
Черная дыра - область пространства, в к-рой поле тяготения настолько сильно, что вторая космич. скорость (параболическая скорость) для находящихся в этой области тел должна была бы превышать скорость света, т.е. из Ч.д. ничто не может вылететь - ни излучение, ни частицы, ибо в природе ничто не может двигаться со скоростью, большей скорости света. Границу области, за к-рую не выходит свет, наз. горизонтом Ч.д. Для того чтобы поле тяготения смогло "запереть" излучение, создающее это поле масса
 должна сжаться до объема с радиусом,
меньшим гравитационного радиуса
должна сжаться до объема с радиусом,
меньшим гравитационного радиуса 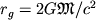 . Гравитац. радиус чрезвычайно мал даже для больших масс (напр., для
Солнца, имеющего массу
. Гравитац. радиус чрезвычайно мал даже для больших масс (напр., для
Солнца, имеющего массу 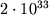 г,
г, 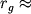 3 км).
3 км).
Поле тяготения Ч.д. описывается теорией тяготения Эйнштейна (см. Тяготение). Согласно этой теории, вблизи Ч.д. геометрич. св-ва пространства описываются неевклидовой (римановой) геометрией, а время течет медленнее, чем вдали, вне сильного поля тяготения.
По совр. представлениям, массивные звезды (с массой в неск.
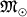 и больше), заканчивая свою эволюцию, могут в конце концов сжаться (сколлапсировать)
и превратиться в Ч.д. (см. Эволюция звезд,
Гравитационный коллапс).
и больше), заканчивая свою эволюцию, могут в конце концов сжаться (сколлапсировать)
и превратиться в Ч.д. (см. Эволюция звезд,
Гравитационный коллапс).
Если Ч.д. возникает при сжатии невращающегося незаряженного тела, то ее внеш. поле тяготения оказывается строго сферическим и зависящим только от полной массы тела
 . Все отклонения от сферичности в граивтац. поле при образовании Ч.д. излучаются
в виде гравитац. волн (см. Гравитационное
излучение). Оставшееся поле не зависит от распределения массы внутри сжавшегося
тела. Т.о., хотя внутри Ч.д. может быть "спрятано" очень несимметрично сжимающееся
тело,
внеш. поле тяготения будет строго сферически-симметричным (т.н. поле Шварцшильда).
. Все отклонения от сферичности в граивтац. поле при образовании Ч.д. излучаются
в виде гравитац. волн (см. Гравитационное
излучение). Оставшееся поле не зависит от распределения массы внутри сжавшегося
тела. Т.о., хотя внутри Ч.д. может быть "спрятано" очень несимметрично сжимающееся
тело,
внеш. поле тяготения будет строго сферически-симметричным (т.н. поле Шварцшильда).
При образовании Ч.д. излучаются также все физ. поля, кроме статического электрического поля (если коллапсирующее тело было электрически заряженным).
Если тело, образовавшее Ч.д., вращалось, то вокруг Ч.д. сохраняется "вихревое" гравитац. поле, увлекающее все тела вблизи Ч.д. во вращательное движение вокруг нее. Это поле определяется помимо массы Ч.д. только ее полным моментом импульса. Поле тяготения вращающейся Ч.д. наз. полем Керра.
2. Поле тяготения невращающейся черной дыры
Движение тел в поле тяготения Шварцшильда обладает рядом особенностей. В теории Ньютона движение по окружности вокруг тяготеющего центра возможно на любом расстоянии R от него. В теории Эйнштейна это не так. Чем ближе к Ч.д., тем больше скорость кругового движения. На окружности с R=1,5 rg скорость движения достигает световой. Ближе к Ч.д. движение по окружности, очевидно, вообще невозможно. В действительности же движение по окружности становится неустойчивым на значительно больших расстояниях, а именно: начиная с R=3 rg, когда скорость движения составляет всего половину световой. Только на расстояниях, превышающих 3rg, возможно устойчивое круговое движение. На пределе устойчивости круговых орбит энергия связи частицы
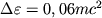 , где m - масса
частицы.
, где m - масса
частицы.
Особый интерес представляет возможность гравитац. захвата черной дырой тел, прилетающих из бесконечности к тяготеющей массе, описывает около нее параболу или гиперболу и (если не испытывает соударения с тяготеющей массой) снова улетает в бесконечность. Гравитац. захват в этой задаче невозможен.
Иначе обстоит дело в поле тяготения Ч.д. Конечно, если тело движется на больших расстояниях от Ч.д. (R>rg), где поле тяготения уже слабо и справедлива с большой точностью теория Ньютона, то траектория движения почти точно совпадает с параболой или гиперболой. В достаточной близости от Ч.д. траектория резко отличается от ньютоновской. Так, если скорость тела вдали от Ч.д. много меньшн световой и траектория его движения подходит близко к окружности с R=2 rg, то тело совершит много оборотов вокруг Ч.д., прежде чем снова улетит в космос (рис. 1, а).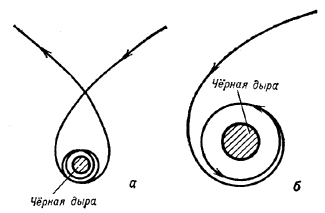
Рис. 1. Наконец, если тело подойдет вплотную к указанной окружности, то его орбита будет неограниченно навиватсья на окружность. Тело окажется гравитационно захваченным Ч.д. и никогда снова не улетит в космос (рис. 1, б). Если же тело подлетит еще ближе к Ч.д., то после неск. оборотов или даже не успев сделать ни одного оборота, оно упадет в Ч.д.
В поле тяготения Ч.д. выражение для параболической скорости записывается формально так же, как и в теории Ньютона. Однако необходимо сделать следующее уточнение. Когда тело движется прямо по радису к Ч.д., то какую бы скорость тело не имело, в т.ч. и больше параболической, оно упадет в Ч.д. Более того, если тело движется хотя и не прямо по радиусу к Ч.д., но траектория его достаточно близка к Ч.д., то оно тоже будет захвачено Ч.д. Следовательно, для того чтобы вырваться из окрестностей Ч.д., мало иметь скорость, превышающую параболическую, надо еще, чтобы угол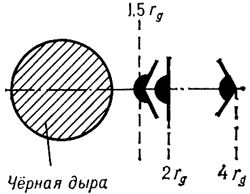
Рис. 2. 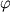 между направлением этой
скорости и направлением на Ч.д. превышал нек-рое критич. значение
между направлением этой
скорости и направлением на Ч.д. превышал нек-рое критич. значение 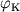 .
При
.
При 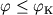 тело окажется захваченным Ч.д., при
тело окажется захваченным Ч.д., при 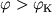 (и условии, что скорость больше или равна параболической) тело улетит
от Ч.д. Значение
(и условии, что скорость больше или равна параболической) тело улетит
от Ч.д. Значение 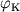 зависит от расстояния до Ч.д. На рис. 2 черным
цветом закрашен конус захвата: если вектор параболической скорости располагается
в этом
конусе, то тело будет захвачено Ч.д.
зависит от расстояния до Ч.д. На рис. 2 черным
цветом закрашен конус захвата: если вектор параболической скорости располагается
в этом
конусе, то тело будет захвачено Ч.д.
Поле тяготения Ч.д. искривляет траектории лучей света (и вообще любых ультрарелятивистских частиц, к-рые движутся практически по тем же траекториям, что и фотоны). Чем ближе к Ч.д. траектории, тем сильнее они искривлены. На рис. 3, а приведены траектории лучей света, испущенных на разных расстояниях от Ч.д. перпендикулярно к радиальному направлению. Для лучей существует критич. окружность с R=1,5 rg. По этой окружности может двигаться фотон, удерживаемый тяготением Ч.д. Однако это движение неустойчиво. При малейшем возмущении фотон либо попадает в Ч.д., либо улетает в космос.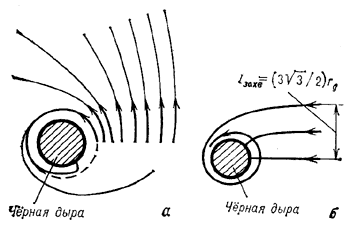
Рис. 3. Наличие критич. окружности ведет к тому, что все лучи с прицельным параметром на бесконечности
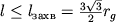 гравитационно захватываются
(рис. 3, б).
гравитационно захватываются
(рис. 3, б).
3. Поле тяготения вращающейся черной дыры
Около вращающейся Ч.д., как уже было сказано, должно существовать "вихревое" гравитац. поле. Вдали от Ч.д. оно очень слабо, а вблизи возрастает настолько, что ведет к качественно новым эффектам.
Так, в окрестности вращающейся Ч.д. возникает область, в к-рой все тела и фотоны увлекатся в движение вокург Ч.д. Внеш. граница этой области наз. пределом статичности. Однако внутри предела статичности тела и фотоны совсем не обязательно должны падать к центру, они могут и приближаться к Ч.д. и удаляться от нее, могут выходить за предел статичности. Т.о., предел статичности не явл. границей Ч.д., ее горизонтом, из-под к-рого нельзя выйти. Линейные размеры предела статичности по порядку величины равны rg. Горизонт Ч.д. расположен глубже, под пределом статичности. Пространство между горизонтом и пределом статичности наз. эргосферой (рис. 4). Предел статичности касается горизонта в полюсах вращающейся Ч.д.
При падении тела на вращающуюся Ч.д. оно сначала отклоняется в своем движении в сторону вращения Ч.д., пересекает границу эргосферы и постепенно приближается к горизонту. Для внеш. наблюдателя свет, испускаемый падающим телом, становится все более красным и менее интенсивным, затем полностью затухает: тело, уйдя под горизонт, становится невидимым для внеш. наблюдателя. На горизонте все тела имеют одну ту же угловую скорость обращения, в какое бы место горизонта ни попадало падающее тело.
Общая для всех падающих тел угловая скорость
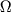 на горизонте Ч.д.
и есть скорость ее вращения:
на горизонте Ч.д.
и есть скорость ее вращения: 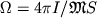 , где I
-
момент импульса тела, из к-рого возникла Ч.д.,
, где I
-
момент импульса тела, из к-рого возникла Ч.д.,  - масса,
S - площадь горизонта Ч.д. Момент импульса Ч.д. заданной массы не может быть
сколь
угодно большим. Максимально возможные значения I и
- масса,
S - площадь горизонта Ч.д. Момент импульса Ч.д. заданной массы не может быть
сколь
угодно большим. Максимально возможные значения I и 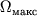 определяются тем, что при образовании Ч.д. линейная скорость вращения точек экватора
тела
не превышает скорости света. По порядку величины
определяются тем, что при образовании Ч.д. линейная скорость вращения точек экватора
тела
не превышает скорости света. По порядку величины 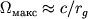 .
Для Ч.д. с массой, равной массе Солнца,
.
Для Ч.д. с массой, равной массе Солнца, 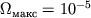 (1/с).
(1/с).
Гравитац. захват частиц Ч.д. с вращением несколько отличается от захвата невращающейся Ч.д. Легче всего захватываются частицы, к-рые пролетают вблизи Ч.д. в сторону, противоположную вращению, труднее захватываются частицы, летящие мимо Ч.д. в сторону вращения. Наглядно можно себе представить, что вихревое гравитац. поле вокруг Ч.д. действует подобно праще, ускоряя, отбрасывая тем самым частицы, движущиеся мимо Ч.д. в ту же сторону, в к-рую закручивается "вихрь" этого поля, и, наоборот, тормозя и захватывая частицы, движущиеся против "вихря".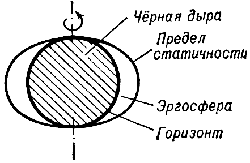
Рис. 4. Рассмотрим для примера захват фотона, движущегося в плоскости экватора максимально быстро вращающейся Ч.д.
Для фотона, движущегося в направлении вращения Ч.д., прицельный параметр lзахв,1=1/2 rg; для фотона, движущегося против вращения, прицельный параметр намного больше: lзахв,2=4 rg. Изменяется ситуация и с круговыми орбитами. Для Ч.д. без вращения последняя устойчивая круговая орбита имеет радиус 3rg; частица, движущаяся по ней, имеет скорость c/2. И самое важное: чтобы попасть на эту орбиту, частица с массой m должна отдать энергию
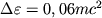 (энергию связи) в виде, напр., гравитационного
излучения.
(энергию связи) в виде, напр., гравитационного
излучения.
В случае максимально быстро вращающейся дыры последняя круговая орбита лежит в экваториальной плоскости близко к горизонту, глубоко внутри эргосферы. Но здесь частица может двигаться только в сторону вращения Ч.д. Энергия, к-рую выделяет частица, попавшая на эту орбиту, гораздо больше и составляет
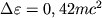 .
В то
же время последняя устойчивая орбита частицы, обращающейся вокруг дыры в противоположном
направлении, лежит вне эргосферы и частица, попадающая в нее, выделяет энергию
.
В то
же время последняя устойчивая орбита частицы, обращающейся вокруг дыры в противоположном
направлении, лежит вне эргосферы и частица, попадающая в нее, выделяет энергию 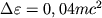 .
.
Полная масса вращающейся Ч.д. определяется как ее размерами (площадью S горизонта), так и энергией вращения:
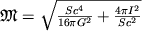 .
.
Если вращение отсутствует (I=0), то
 определяется
только размерами Ч.д. При максимально возможной скорости вращения Ч.д. второе слагаемое
под корнем равно первому.
определяется
только размерами Ч.д. При максимально возможной скорости вращения Ч.д. второе слагаемое
под корнем равно первому.
4. Физические процессы в поле тяготения черной дыры
В эргосфере Ч.д. возможны процессы, приводящие к уменьшению энергии вращения Ч.д., т.е., как оказывается, Ч.д. может терять энергию. В частности, когда в эргосферу влетае частица, имевшая вдали от Ч.д. энергию
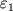 (включая энергию
покоя), и распадается на две частицы, то распад может произойти таким образом, что
одна
частица упадет на Ч.д., а другая, сравнительно немного увеличив свою скорость в момент
распада, перейдет на такую орбиту, что вылетит из эргосферы с огромной скоростью.
Эта
скорость может намного превышать и первоначальную скорость подлета частицы к эргосфере,
и величину изменения скорости при распаде. В результате полная энергия вылетевшей
частицы
(включая энергию
покоя), и распадается на две частицы, то распад может произойти таким образом, что
одна
частица упадет на Ч.д., а другая, сравнительно немного увеличив свою скорость в момент
распада, перейдет на такую орбиту, что вылетит из эргосферы с огромной скоростью.
Эта
скорость может намного превышать и первоначальную скорость подлета частицы к эргосфере,
и величину изменения скорости при распаде. В результате полная энергия вылетевшей
частицы
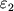 окажется больше
окажется больше 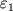 . Избыток энергии
. Избыток энергии
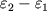 черпается из энергии вращения Ч.д. Энергия
вращения Ч.д. может уменьшаться также при рассеянии эл.-магн. волн на Ч.д. Рассеянная
волна при определенных условиях может оказаться интенсивнее падающей. Потеря энергии
вращения Ч.д. при распаде частицы в эргосфере достигает максимума, когда распад происходит
на горизонте. При этом площадь горизонта не ме
черпается из энергии вращения Ч.д. Энергия
вращения Ч.д. может уменьшаться также при рассеянии эл.-магн. волн на Ч.д. Рассеянная
волна при определенных условиях может оказаться интенсивнее падающей. Потеря энергии
вращения Ч.д. при распаде частицы в эргосфере достигает максимума, когда распад происходит
на горизонте. При этом площадь горизонта не ме