Пульсации звезд
[физика космоса]
собственные колебания колебания звезд, проявляющиеся в их периодическом сжатии и расширении. Простейший вид собств. колебаний звезды - радиальные сферически-симметричные пульсации, при к-рых она периодически расширяется и сжимается, сохраняя при этом форму шара (в общем случае нерадиальных колебаний меняется и форма звезды, напр., звезда периодически принимает форму то вытянутого, то сплюснутого эллипсоида). По совр.
[Цитировать][Ответить][Новое сообщение]
| Форумы >> Обсуждение публикаций Астронета |
| Список / Дерево Заголовки / Аннотации / Текст |
- >> Пульсации звезд
(С. А. Жевакин, А. А. Памятных, "Физика Космоса", 1986,
30.03.2003 21:02, 26.4 КБайт, ответов: 1)
собственные колебания колебания звезд, проявляющиеся в их периодическом сжатии и
расширении. Простейший вид собств. колебаний звезды - радиальные сферически-симметричные
пульсации,
при к-рых она периодически расширяется и сжимается, сохраняя при этом форму шара
(в общем случае нерадиальных колебаний меняется и форма звезды, напр., звезда периодически
принимает форму то вытянутого, то сплюснутого эллипсоида).
По совр. представлениям, переменность цефеид, звезд типов RV Тельца, RR Лиры,
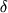 Щита,
Щита, 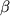 Цефея, ZZ
Кита
(белых карликов) и некоторых др. типов физ.
переменных звезд обусловлена их П.
Цефея, ZZ
Кита
(белых карликов) и некоторых др. типов физ.
переменных звезд обусловлена их П.
Внутр. строение большинства пульсирующих звезд таково, что они обладают значит. концентрацией массы к центру: плотность вещества в центре на неск. порядков превышает ср. плотность звезды. Особенно сильно это выражено у гигантов и сверхгигантов (к к-рым относятся, напр., цефеиды и переменные типа RR Лиры), в меньшей степени - у звезд вблизи главной последовательности (переменные типа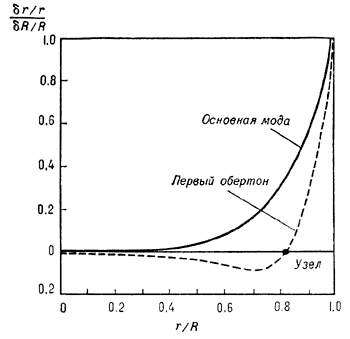
Рис. 1. Поведение относительной амплитуды 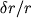
малых радиальных колебаний в пульсирующей
звезде-гиганте (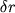 - амплитуда смещения
- амплитуда смещения
на расстоянии r от центра звезды,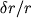 выражена
выражена
в единицах относительной амплитуды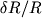 на поверхности
на поверхности
звезды, R - радиус звезды). Сплошная линия - колебания
на основной частоте, штриховая - на частоте первого
обертона. Колебания на частоте первого обертона имеют узел
при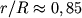 .
.
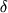 Щита,
Щита, 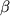 Цефея), но даже и у
них центральная плотность в 100-1000 раз больше средней и на много порядков больше
плотности
вещества на поверхности. Из-за неоднородного (по плотности) распределения вещества
П. негомологичны: относительные амплитуды колебаний в центре намного меньше, чем
на поверхности.
Поведение относительной амплитуды
Цефея), но даже и у
них центральная плотность в 100-1000 раз больше средней и на много порядков больше
плотности
вещества на поверхности. Из-за неоднородного (по плотности) распределения вещества
П. негомологичны: относительные амплитуды колебаний в центре намного меньше, чем
на поверхности.
Поведение относительной амплитуды 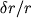 малых радиальных колебаний
в модели пульсирующей звезды показано на рис. 1, где сплошная линия соответствует
т.н.
осн. моде (собств. колебаниям с наибольшим периодом), штриховая лииня - первому обертону,
период к-рого меньше, чем для осн. моды, и к-рый характеризуется наличием одного
узла вдоль радиуса. Второй обертон имеет два узла вдоль радиуса, третий - три, и
т.д. Колебания с разных сторон узла происходят в противофазе: когда внеш. область
расширяется,
внутренняя сжимается. В большинстве пульсирующих звезд колебания представляют собой
стоячие волны, и поэтому положения узлов (в случае обертонных пульсаций) со временем
не
меняются.
малых радиальных колебаний
в модели пульсирующей звезды показано на рис. 1, где сплошная линия соответствует
т.н.
осн. моде (собств. колебаниям с наибольшим периодом), штриховая лииня - первому обертону,
период к-рого меньше, чем для осн. моды, и к-рый характеризуется наличием одного
узла вдоль радиуса. Второй обертон имеет два узла вдоль радиуса, третий - три, и
т.д. Колебания с разных сторон узла происходят в противофазе: когда внеш. область
расширяется,
внутренняя сжимается. В большинстве пульсирующих звезд колебания представляют собой
стоячие волны, и поэтому положения узлов (в случае обертонных пульсаций) со временем
не
меняются.
Период P собств. колебаний звезды при том или ином типе колебаний (для к.-л. моды) определяется в основном ср. плотностью вещества звезды
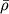 (т.е.
в конечном счете ее полной массой
(т.е.
в конечном счете ее полной массой 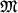 и радиусом R).
Это теоретич. соотношение имеет вид
и радиусом R).
Это теоретич. соотношение имеет вид 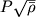 = const, где "постоянная"
различна для разных мод, и, кроме того, она немного зависит от внутр. строения звезды
(в частности, чем больше концентрация вещества к центру, тем меньше период осн. моды
при заданных
= const, где "постоянная"
различна для разных мод, и, кроме того, она немного зависит от внутр. строения звезды
(в частности, чем больше концентрация вещества к центру, тем меньше период осн. моды
при заданных 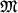 и R). Периоды большинства переменных
звезд согласуются с гипотезой радиальных колебаний в осн. моде, но у нек-рых звезд
наблюдается,
по-видимому, П. в обертонах или даже одновременно в неск. модах (в т.ч. и нерадиальных).
Для звезд конкретного типа переменности, напр., типа RR Лиры, имеющих сходное строение,
соотношение
и R). Периоды большинства переменных
звезд согласуются с гипотезой радиальных колебаний в осн. моде, но у нек-рых звезд
наблюдается,
по-видимому, П. в обертонах или даже одновременно в неск. модах (в т.ч. и нерадиальных).
Для звезд конкретного типа переменности, напр., типа RR Лиры, имеющих сходное строение,
соотношение 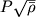 =const хорошо выполняется.
=const хорошо выполняется.
В пульсирующей звезде, за исключением ее самых внешних областей, колебания происходят почти адиабатически (см. Адиабатический процесс), в том смысле, что в течение цикла колебаний любой выделенный в звезде слой никак не изменяет проходящий через него поток излучения и пульсирует как бы в условиях полной теплоизоляции, без теплообмена с окружающими слоями. Анализ адиабатич. П. не может дать никакой информации о пульсационной устойчивости звезды, т.е. о том, будут ли малые колебания нарастать или затухать с течением времени. Однако такой анализ обычно дает хорошее описание механич. св-в звезды, в частности весьма точные значения периодов и правильное представление о распределении амплитуды П. вдоль радиуса.
Хотя неадиабатич. эффекты и малы, они приводят к медленному изменению амплитуды П. Очевидно, если в момент наибольшего сжатия выделенный в звезде слой получает нек-рое количество теплоты, то последующее расширение будет происходить при большем давлении, чем произошло сжатие. В результате работа, совершенная слоем за цикл колебаний, будет положительной, т.е., как и в любой тепловой машине, будет иметь место превращение тепловой энергии в механическую. Такой слой будет вносить вклад в возбуждение (раскачку) колебаний. Если же в момент наибольшего сжатия слой теряет теплоту, то он вносит вклад в затухание колебаний. Если суммарная работа всех слоев в звезде за цикл колебаний положительна, то звезда пульсационно неустойчива (колебания нарастают), в противоположном случае - устойчива (колебания затухают).
Накопление или потеря теплоты выделенным слоем звездного вещества (если в слое нет источников энергии) связаны с тем, какое изменение претерпевает идущий через слой поток излучения. В большинстве звезд поток излучения в момент наибольшего сжатия возрастает в направлении от центра к поверхности, т.е. через внеш. границу выделенного слоя выходит больше теплоты, чем поступает в слой через внутр. границу. Каждый слой в момент наибольшего сжатия теряет теплоту и способствует затуханию колебаний (звезда устойчива). Такое поведение потока излучения при сжатии обусловлено в основном изменениями коэффициента непрозрачности звездного вещества. Обычно при сжатии коэффициент непрозрачности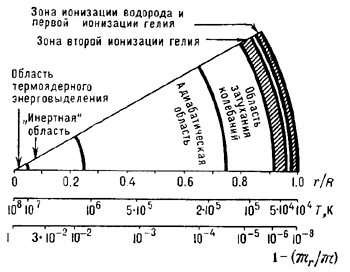
Рис. 2. Схематическое расположение областей,
определяющих основные особенности пульсаций
модели переменной звезды типа RR Лиры. Нижняя
шкала указывает доли звездной массы, отсчитываемой
от поверхности ("инертная" область в объеме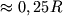
от центра содержит свыше 99% массы звезды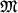 ,
,
а масса зон ионизации всего лишь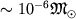 ).
).
 уменьшается, причем из-за негомологичности колебаний уменьшение на внешней границе
выделенного слоя будет б'ольшим, чем на внутренней, и поэтому слой будет терять теплоту.
Некоторый отток теплоты из слоя при сжатии может иметь место и при постоянном
уменьшается, причем из-за негомологичности колебаний уменьшение на внешней границе
выделенного слоя будет б'ольшим, чем на внутренней, и поэтому слой будет терять теплоту.
Некоторый отток теплоты из слоя при сжатии может иметь место и при постоянном  .
Дело в том, что поток излучения пропорционален довольно высокой (обычно
четвертой) степени темп-ры, а темп-ра при сжатии, как правило, возрастает. Поэтому
при негомологичности колебаний должен происходить отток теплоты из слоя в момент
наибольшего
сжатия. Согласно расчетам, время затухания колебаний в звездах-гигантах и сверхгигантах
должно составлять от сотен дней до неск. лет, т.е., казалось бы, мы вообще не должны
наблюдать пульсирующих звезд (а если случайно такая звезда обнаружится, амплитуда
ее П. должна уменьшаться "на глазах"). Существование большого числа длительно пульсирующих
звезд указывает на то, что в пульсирующей звезде должен постоянно действовать эффективный
механизм раскачки колебаний. На первый взгляд, такой механизм действует в недрах
звезд, где протекают термоядерные реакции, интенсивность к-рых сильно зависит от
темп-ры: при сжатии темп-ра возрастает, и вследствие этого усиливается выделение
ядерной энергии.
При расширении, наоборот, выделение энергии уменьшается. Однако из-за чрезвычайно
малых амплитуд колебаний в центре раскачивающий эффект, вызванный периодич. усилением
термоядерных
реакций, оказывается незначительным в сравнении с затуханием во внеш. слоях. Т.о.,
негомологичность собств. колебаний звезд заставляет отказаться от рассмотрения к.-л.
"центральных"
механизмов возбуждения П. и искать механизмы раскачки, локализованные во внеш. слоях.
Самым эффективным из найденных механизмов для классич. переменных звезд (цефеид,
переменных
типа RR Лиры и др. звезд в полосе неустойчивости, см. Эволюция звезд) оказалось действие зон частичной ионизации водорода и
гелия,
особенно зоны второй ионизации гелия.
.
Дело в том, что поток излучения пропорционален довольно высокой (обычно
четвертой) степени темп-ры, а темп-ра при сжатии, как правило, возрастает. Поэтому
при негомологичности колебаний должен происходить отток теплоты из слоя в момент
наибольшего
сжатия. Согласно расчетам, время затухания колебаний в звездах-гигантах и сверхгигантах
должно составлять от сотен дней до неск. лет, т.е., казалось бы, мы вообще не должны
наблюдать пульсирующих звезд (а если случайно такая звезда обнаружится, амплитуда
ее П. должна уменьшаться "на глазах"). Существование большого числа длительно пульсирующих
звезд указывает на то, что в пульсирующей звезде должен постоянно действовать эффективный
механизм раскачки колебаний. На первый взгляд, такой механизм действует в недрах
звезд, где протекают термоядерные реакции, интенсивность к-рых сильно зависит от
темп-ры: при сжатии темп-ра возрастает, и вследствие этого усиливается выделение
ядерной энергии.
При расширении, наоборот, выделение энергии уменьшается. Однако из-за чрезвычайно
малых амплитуд колебаний в центре раскачивающий эффект, вызванный периодич. усилением
термоядерных
реакций, оказывается незначительным в сравнении с затуханием во внеш. слоях. Т.о.,
негомологичность собств. колебаний звезд заставляет отказаться от рассмотрения к.-л.
"центральных"
механизмов возбуждения П. и искать механизмы раскачки, локализованные во внеш. слоях.
Самым эффективным из найденных механизмов для классич. переменных звезд (цефеид,
переменных
типа RR Лиры и др. звезд в полосе неустойчивости, см. Эволюция звезд) оказалось действие зон частичной ионизации водорода и
гелия,
особенно зоны второй ионизации гелия.
Расположение в звездах типа RR Лиры областей, ответственных за возбуждение и затухание П., показано на рис. 2. Равновесный радиус этих звезд составляет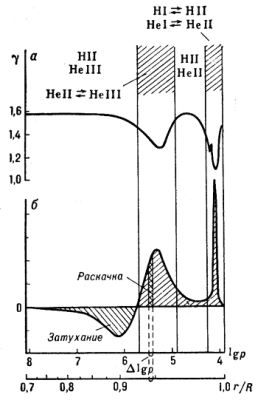
Рис. 3. а - Изменение показателя адиабаты 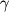
в звезде типа RR Лиры с глубиной (общее строение
звезды показано на рис. 2). Заштрихованы области
частичной ионизации. б - Вклад различных слоев звезды
в возбуждение или затухание малых колебаний. Слой
толщиной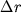 совершает за полный цикл колебаний
совершает за полный цикл колебаний
работу, измеряемую площадью с двойной штриховкой. Зона
HeII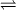 HeIII дает вклад
HeIII дает вклад 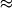 75-80%
в возбуждение
75-80%
в возбуждение
пульсаций. Суммарная работа всех слоев (заштрихованная
площадь с учетом знака работы) положительна, поэтому
звезда пульсационно неустойчива.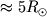 ,
эффективная темп-ра
,
эффективная темп-ра 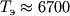 К, светимость
К, светимость 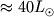 ,
темп-ра в центре
,
темп-ра в центре 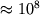 К, а плотность в центре
К, а плотность в центре 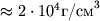 (
(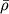 в 2 млрд. раз меньше).
Ионизация водорода и первая ионизация гелия происходят при темп-рах от
в 2 млрд. раз меньше).
Ионизация водорода и первая ионизация гелия происходят при темп-рах от 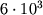 до
до  К, вторая ионизация гелия - от
К, вторая ионизация гелия - от 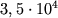 до
до 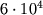 К. Эти области простираются вглубь менее чем на 0,1R,
однако именно они обеспечивают раскачку и поддержание П. Осн. затухание происходит
в области с температурой от
К. Эти области простираются вглубь менее чем на 0,1R,
однако именно они обеспечивают раскачку и поддержание П. Осн. затухание происходит
в области с температурой от 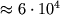 К у верхней границы
до
К у верхней границы
до
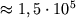 К у нижней. Более глучокие слои пульсируют практически адиабатически
и не влияют на устойчивость звезды. На внеш. границе еще более глубокой "инертной"
области амплитуда колебаний не превышает 1/1000 поверхностной амплитуды, и эту область
(вплоть до центра) при анализе П. можно уверенно считать "жестким" ядром звезды.
К у нижней. Более глучокие слои пульсируют практически адиабатически
и не влияют на устойчивость звезды. На внеш. границе еще более глубокой "инертной"
области амплитуда колебаний не превышает 1/1000 поверхностной амплитуды, и эту область
(вплоть до центра) при анализе П. можно уверенно считать "жестким" ядром звезды.
Раскачавающее действие зон частичной ионизации основано на том, что при сжатии они способны несколько задерживать проходящий через них поток излучения, а при расширении - наоборот, усиленно терять энергию, отдавая ее внешним слоям. Действительно, в зоне частичной ионизации энергия, выделяющаяся при сжатии, идет не только на нагрев газа, но и на его ионизацию. Это препятствует сильному повышению темпратуры при сжатии. [Относительные изменения плотности
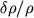 связаны с относительными изменениями
темп-ры
связаны с относительными изменениями
темп-ры 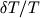 соотношением
соотношением 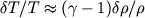 ,
строго выполняющимся лишь при адиабатич. колебаниях.] В зоне второй
ионизации гелия
,
строго выполняющимся лишь при адиабатич. колебаниях.] В зоне второй
ионизации гелия 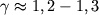 (рис. 3) вместо обычного значения
(рис. 3) вместо обычного значения
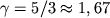 для идеального одноатомного газа, т.е. при сжатии
повышение темп-ры в зоне ионизации оказывается меньшим, чем в прилегающих более глубоких
слоях. Для заданного коэфф. непрозрачности поток излучения пропорционален T4,
а поэтому при сжатии в зоне ионизации произойдет задержка потока излучения, идущего
изнутри. Данный эффект, связанный с прямым влиянием изменений темп-ры на поток излучения,
наз.
для идеального одноатомного газа, т.е. при сжатии
повышение темп-ры в зоне ионизации оказывается меньшим, чем в прилегающих более глубоких
слоях. Для заданного коэфф. непрозрачности поток излучения пропорционален T4,
а поэтому при сжатии в зоне ионизации произойдет задержка потока излучения, идущего
изнутри. Данный эффект, связанный с прямым влиянием изменений темп-ры на поток излучения,
наз. 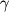 -механизмом. Значительную, если не осн. роль играют и изменения
непрозрачности. Коэффициент непрозрачности
-механизмом. Значительную, если не осн. роль играют и изменения
непрозрачности. Коэффициент непрозрачности 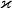 зависит от T
и
зависит от T
и 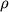 по закону
по закону 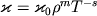 (
(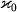 - постоянная величина для вещества данного хим. состава,
- постоянная величина для вещества данного хим. состава, 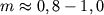 ,
, 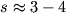 ). Из-за малых вариаций темп-ры в зоне ионизации
при П. изменения плотности становятся определяющими в законе непрозрачности, т.е.
при сжатии непрозрачность будет увеличиваться (в др. областях звезды она уменьшается
из-за сильного повышения темп-ры). Поток излучения обратно пропорционален коэфф.
). Из-за малых вариаций темп-ры в зоне ионизации
при П. изменения плотности становятся определяющими в законе непрозрачности, т.е.
при сжатии непрозрачность будет увеличиваться (в др. областях звезды она уменьшается
из-за сильного повышения темп-ры). Поток излучения обратно пропорционален коэфф.
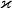 ,
поэтому из-за увеличения
,
поэтому из-за увеличения 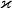 в зоне ионизации при сжатии (рис.
4) также произойдет задержка излучения. Кроме того, в зоне ионизации водорода поакзатель
s становится малым или даже отрицательным, что способствует еще большему увеличению
в зоне ионизации при сжатии (рис.
4) также произойдет задержка излучения. Кроме того, в зоне ионизации водорода поакзатель
s становится малым или даже отрицательным, что способствует еще большему увеличению
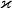 при сжатии. В целом эффект, связанный с прямым влиянием изменений
непрозрачности на поток излучения наз.
при сжатии. В целом эффект, связанный с прямым влиянием изменений
непрозрачности на поток излучения наз. 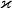 -механизмом. Следует
отметить, что
-механизмом. Следует
отметить, что 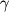 -механизм и
-механизм и 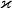 -механизм не явл.
независимыми,
их разделение несколько искусственное.
-механизм не явл.
независимыми,
их разделение несколько искусственное.
Рассмотренные эффекты изменений темп-ры и непрозрачности сами по себе еще недостаточны для обеспечения раскачки П. Во внутр. частях зоны ионизации, где
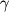 уменьшается в направлении от центра (достигая минимума ок. середины зоны), происходит
задержка потока излучения при сжатии; во внеш. же частях этой зоны, где
уменьшается в направлении от центра (достигая минимума ок. середины зоны), происходит
задержка потока излучения при сжатии; во внеш. же частях этой зоны, где 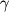 увеличивается в направлении от центра, при сжатии может происходить усиленный отток
теплотыЮ и тогда эта внеш. часть будет вносить вклад в затухание П. Затухание будет
иметь
место в области над зоной ионизации, где показатель
увеличивается в направлении от центра, при сжатии может происходить усиленный отток
теплотыЮ и тогда эта внеш. часть будет вносить вклад в затухание П. Затухание будет
иметь
место в области над зоной ионизации, где показатель 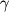 приблизительно
постоянен, а коэфф.
приблизительно
постоянен, а коэфф. 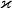 при сжатии уменьшается. При этом суммарный
раскачивающий эффект зоны ионизации может оказаться малым или вообще отсутствовать,
особенно при негомологичности колебаний (в данном случае при больших изменениях физ.
параметров
в ходе П. во внеш. части зоны по сравнению с внутр. областью).
при сжатии уменьшается. При этом суммарный
раскачивающий эффект зоны ионизации может оказаться малым или вообще отсутствовать,
особенно при негомологичности колебаний (в данном случае при больших изменениях физ.
параметров
в ходе П. во внеш. части зоны по сравнению с внутр. областью).
Однако из-за очень низкой плотности самых внеш. слоев их П. характеризуются сильной неадиабатичностью (сильным теплообменом между отдельными слоями), и оказывается, что такие разреженные слои неспособны эффективно задерживать проходящий через них поток излучения: в любой момент времени выделенный слой теряет через свою внеш. границу столько же энергии, сколько получает ее изнутри. Т.о., самые внешние слои не вносят никакого вклада в возбуждение или затухание П.
Для того чтобы зона ионизации создавала заметный раскачивающий эффект, она должна располагаться на нек-рой оптимальной глубине под поверхностью звезды, т.е. так, чтобы во внутр. ее части происходило сильное возбуждение П., и в то же время во внеш. части и выше нее благодаря неадиабатич. эффектам практически отсутствовало затухание. Именно такая ситуация, по-видимому, реализуется в зоне HeII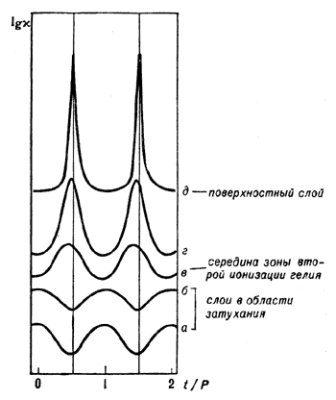
Рис. 4. Изменение коэффициента непрозрачности 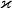
во внешних слоях модели классической цефеиды с течением
времени t (охвачены два периода P установившихся пульсаций).
Вертикальные линии отмечают моменты ниабольшего сжатия.
В эти моменты значения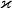 близки к максимальному значению
близки к максимальному значению
в зонах частичной ионизации водорода и гелия (слои в-д) и к
минимальному (слои а-б). (По данным Дж. Кокса) HeIII
переменных звезд. Вторая ионизация He происходит при темп-ре ок.
HeIII
переменных звезд. Вторая ионизация He происходит при темп-ре ок. 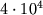 К (в середине зоны) в соответствии с потенциалом ионизации 54,4 эВ. Поэтому в звездах
с разной эффективной темп-рой Tэ зона ионизации
расположена
на различной глубине под поверхностью. Если она слишком близка к поверхности (Tэ
слишком велика), то колебания всей зоны характеризуются сильной
неадиабатичностью и зона не вносит вклада в возбуждение П. Если же зона лежит слишком
глубоко (Tэ слишком мала), неадиабатические эффекты
малы по всей зоне, и поэтому раскачивающее действие внутр. части зоны компенсируется
затуханием во внеш. части и зона также практически не вносит вклада в возбуждение
П. Т.о.,
должен существовать довольно узкий диапазон значений Tэ,
для к-рого возможно возбуждение П. в зоне второй ионизации гелия. Существование узкой,
почти вертикальной полосы неустойчивости на диаграмме Герцшпрунга-Ресселла, населенной переменными звездами, явл.
доказательством
эффективного действия рассмотренного ионизационного механизма в классических переменных
звездах. Очевидно, что подобная пульсационная неустойчивость сильно зависит от содержания
(обилия) гелия Y: ширина теоретической полосы
неустойчивости увеличивается с увеличением Y. Наилучшее согласие с наблюдениями
(особенно это касается положения высокотемпературной границы полосы неустойчивости)
достигается при предположении, что обилие гелия в пульсирующих звездах составляет
ок. 30%
(по массе). Эта оценка согласуется с другими независимыми определениями Y
в осн. типах переменных звезд.
К (в середине зоны) в соответствии с потенциалом ионизации 54,4 эВ. Поэтому в звездах
с разной эффективной темп-рой Tэ зона ионизации
расположена
на различной глубине под поверхностью. Если она слишком близка к поверхности (Tэ
слишком велика), то колебания всей зоны характеризуются сильной
неадиабатичностью и зона не вносит вклада в возбуждение П. Если же зона лежит слишком
глубоко (Tэ слишком мала), неадиабатические эффекты
малы по всей зоне, и поэтому раскачивающее действие внутр. части зоны компенсируется
затуханием во внеш. части и зона также практически не вносит вклада в возбуждение
П. Т.о.,
должен существовать довольно узкий диапазон значений Tэ,
для к-рого возможно возбуждение П. в зоне второй ионизации гелия. Существование узкой,
почти вертикальной полосы неустойчивости на диаграмме Герцшпрунга-Ресселла, населенной переменными звездами, явл.
доказательством
эффективного действия рассмотренного ионизационного механизма в классических переменных
звездах. Очевидно, что подобная пульсационная неустойчивость сильно зависит от содержания
(обилия) гелия Y: ширина теоретической полосы
неустойчивости увеличивается с увеличением Y. Наилучшее согласие с наблюдениями
(особенно это касается положения высокотемпературной границы полосы неустойчивости)
достигается при предположении, что обилие гелия в пульсирующих звездах составляет
ок. 30%
(по массе). Эта оценка согласуется с другими независимыми определениями Y
в осн. типах переменных звезд.
Аналогично зоне второй ионизации гелия могут действовать зоны ионизации водорода и первой ионизации гелия, поскольку и в них показатель адиабаты
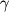 мал (рис.
3, а), а коэффициент непрозрачности при сжатии сильно возрастает (рис. 4, пик в поверхностном
слое). Но вклад этих зон в возбуждение П. невелик, поскольку они располагаются
обычно в разреженных поверхностных слоях. Лишь для относительно холодных звезд ионизация
водорода происходит в достаточно плотных слоях, и тогда эта зона частичной ионизации
может вносить существенный вклад в раскачку П. Однако в оболочках холодных звезд
перенос энергии осуществляется преимущественно конвекцией,
к-рая, по-видимому, препятствует возбуждению П. Почти несомненно, что именно появление
эффективной конвекции во внеш. слоях звезд и определяет положение низкотемпературной
границы полосы неустойчивости на диаграмме Герцшпрунга-Ресселла.
мал (рис.
3, а), а коэффициент непрозрачности при сжатии сильно возрастает (рис. 4, пик в поверхностном
слое). Но вклад этих зон в возбуждение П. невелик, поскольку они располагаются
обычно в разреженных поверхностных слоях. Лишь для относительно холодных звезд ионизация
водорода происходит в достаточно плотных слоях, и тогда эта зона частичной ионизации
может вносить существенный вклад в раскачку П. Однако в оболочках холодных звезд
перенос энергии осуществляется преимущественно конвекцией,
к-рая, по-видимому, препятствует возбуждению П. Почти несомненно, что именно появление
эффективной конвекции во внеш. слоях звезд и определяет положение низкотемпературной
границы полосы неустойчивости на диаграмме Герцшпрунга-Ресселла.
Анализ пульсационной устойчивости звезды относительно малых возмущений (т.н. линейный анализ устойчивости) еще не дает представления об амплитуде усатновившихся П. (а также о форме кривых блеска и лучевой скорости), он лишь указывает на возможность экспоненциального роста или затухания колебаний. Зависимость эффективности механизмов возбуждения
Теория радиальных колебаний, возбуждаемых ионизационными механизмами, хорошо объясняет осн. особенности П.з. в полосе неустойчивости (цефеиды, переменные типа RR Лиры,
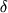 Щита), хотя ряд вопросов еще не решен. П. долгопериодических, полуправильных и неправильных
переменных изучены значительно хуже, отчасти из-за трудностей, связанных с необходимостью
учета взаимодействия П. с конвекцией, очень эффективной в оболочках этих звезд. Переменность
белых карликов и нек-рых звезд типа
Щита), хотя ряд вопросов еще не решен. П. долгопериодических, полуправильных и неправильных
переменных изучены значительно хуже, отчасти из-за трудностей, связанных с необходимостью
учета взаимодействия П. с конвекцией, очень эффективной в оболочках этих звезд. Переменность
белых карликов и нек-рых звезд типа 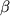 Цефея связана, вероятно,
с их нерадиальными колебаниями, однако механизмы возбуждения П. этих звезд пока неизвестны.
Солнце также явл., по-видимому, пульсирующей звездой, испытывающей различные виды
радиальных и нерадиальных колебаний с периодами от нескольких минут до нескольких
часов (см. Колебания и волны на
Солнце).
Цефея связана, вероятно,
с их нерадиальными колебаниями, однако механизмы возбуждения П. этих звезд пока неизвестны.
Солнце также явл., по-видимому, пульсирующей звездой, испытывающей различные виды
радиальных и нерадиальных колебаний с периодами от нескольких минут до нескольких
часов (см. Колебания и волны на
Солнце).
Лит.:
Жевакин С.А., Теория звездных пульсаций, в кн.: Пульсирующие звезды, М., 1970; Кокс Дж., Теория звездных пульсаций, пер. с англ., М., 1983.(С.А. Жевакин, А.А. Памятных)
- Re: Пульсации звезд (В. Н. Гладышев, 12.02.2009 21:09, 21.1 КБайт) Представления Эддингтона и Жевакина о механизме звездных пульсаций не выглядят убедительно с позиций теории колебаний. Точка зрения Голда и Пачини на природу пульсаров приводит к абсурдным следствиям. Ниже изложен взгляд на природу звездных пульсаций, позволяющий проблемы непротивореиво объединить. К сожалению, вложить рисунки не удалось. Они могут быть высланы by e-mail по запросу. С математической стороной задачи можно познакомиться по ссылкам. О звездных пульсациях. Гладышев В.Н. glavanik@yandex.ru Еще во времена Гиппарха было замечено, что яркость некоторых звезд изменяется. Две с лишним тысячи лет астрономических наблюдений позволили установить, что яркость одних звезд изменяется случайно, других очень строго периодически. Периодическое изменение яркости связывают с их пульсациями. Периоды пульсаций разных звезд значительно различаются. Это позволило разделить их на группы, отличающиеся главным образом периодом колебаний. Деление это не очень строгое, но существует [1]. Например, периоды долгопериодических переменных лежат в интервале 100 700 суток, звезды типа RV Тельца 20 150 суток, классические цефеиды 1 50 суток, звезды типа W Девы 2 45 суток, цефеиды с биениями 1 7 суток, звезды типа RR Лиры 1,5 24 часа, звезды типа Цефея 4 6 часов, карликовые цефеиды 1 3 часа, переменные белые карлики 200 1000 секунд. В последние десятилетия были открыты такие источники периодического электромагнитного излучения (ЭМИ) как магнитары и пульсары, характерные на сегодня длительности периодов повторения излучения которых лежат в интервале от нескольких миллисекунд до 12 секунд. Более того, если для первой группы медленных звезд изменение яркости излучения имеет форму, близкую к синусоидальной или к сумме двух-трех синусоид разной частоты, то для магнитаров и пульсаров типична импульсная форма сигнала. Такая большая разница временных характеристик и формы излучения звезд вынуждает искать разные модели для их описания. Около 1920 г. Эддингтон предложил модель поддержания периодических колебаний в звезде, в основу которой было положено предположение, что в звезде имеется зона, работающая как ключ, периодически открывающий или перекрывающий путь потоку излучения. Первоначально предполагалось, что такой зоной является зона ионизации водорода, происходящей при температуре порядка 10 тысяч К (кельвин). Однако, вскоре выяснилось, что пульсации возникают и в звездах, поверхностная температура которых превышает 30 тысяч К, т.е. в звезде нет зоны ионизации водорода, но пульсации в такой звезде все-таки возникают. Казалось, теория рухнула. Но Жевакин предложил считать, что ключом является зона второй ионизации гелия, которая происходит при температуре порядка 40-60 тысяч К. Таким образом, поскольку поверхностная температура всех известных звезд ниже температуры второй ионизации гелия, теория была спасена. Процессу ионизации водорода, как и первой ионизации гелия, была отведена роль некой частности, существенной роли в большинстве звезд не играющей. Остается не выясненной роль происходящих в звезде термоядерных реакций. Если Эддингтон отмечал их важную роль в колебательном процессе, то Кокс в этом сомневается. Он считает, что в центральных областях звезды, где эти реакции происходят, движения плазмы малы по сравнению с ее движениями в областях вблизи поверхности звезды. Представляется, что в этих взглядах слишком много неопределенностей для того, чтобы считать их установившимися. После открытия пульсаров возник вопрос, какова их сущность? Поскольку представления о механизме периодичного излучения цефеид уже существовали, то были предприняты попытки представить причины нестационарности пульсаров аналогично. Но возникли трудности, связанные с очень короткими длительностями периодов повторения их сигналов. У первых открытых пульсаров они составляли порядка 0,5 1,5 секунды. Пульсировать так быстро на основной частоте обычные звезды, в том числе самые маленькие, не могут. Были предложения объяснять высокую частоту повторения сигнала пульсациями звезды на высоких гармониках их собственных колебаний. Но не удалось объяснить, как в звезде возникают пульсации на высшей гармонике без пульсаций на основной частоте. Были попытки объяснить природу пульсаций сигналов пульсаров вращением традиционных звезд. Но и вращаться с такой скоростью они также не могут, поскольку будут разорваны центробежными силами. Предсказанные теоретически нейтронные звезды пульсировать с такой частотой тоже не могут: они для этого слишком малы. Тогда Голд и Пачини независимо друг от друга с разных сторон пришли к модели быстро вращающейся намагниченной нейтронной звезды с горячей точкой на ее поверхности, излучающей в узком луче электромагнитную энергию. В такой модели наблюдатель, если ему очень повезло, периодически оказывается в луче и воспринимает излучение как последовательность электромагнитных импульсов во всем спектре излучения звезды. Сегодня эта модель пульсара общепринята. Но и она не безупречна. Возникает ряд вопросов, без ответа на которые гипотеза Голда Пачини не выдерживает критики. Основные возражения состоят в следующем. 1. Прежде всего, утверждение, что пульсары являются нейтронными звездами, лишено реальности, поскольку нельзя полагать, что реальность существования самих нейтронных звезд доказана. Подтверждением такой реальности были объявлены пульсары. Логика этого утверждения была очень проста: если теоретически предсказанные нейтронные звезды существуют, а приписываемые им свойства позволяют объяснять некоторые особенности наблюдаемого излучения пульсаров, то пульсары - нейтронные звезды. Но если пульсары нейтронные звезды, то нейтронные звезды существуют. Удивительно, что сама эта излишняя простота суждения не привлекла к себе внимания авторов и сторонников гипотезы. Очевидно, сказалась победная эйфория: впервые теоретически предсказанные астрономические объекты открыты! Других, более аргументированных, доказательств реальности нейтронных звезд и обоснованности их идентификации с пульсарами пока тоже не существует. Поэтому и сами нейтронные звезды, и доказательства их реальности пока еще предстоит искать и обнаруживать. 2. Если существование нейтронных звезд возможно, простые оценки на основе сложившихся теоретических представлений о них говорят нам, что плотность вещества нейтронных звезд должна превышать плотность вещества ядер на порядок и более. Но нам не так уж много известно о свойствах ядерного вещества. Тем более, мы ничего не знаем о веществе в 10 раз более плотном. Мы вообще не знаем, возможно ли существование такого вещества. Можно что-то предполагать, но что-то утверждать и строить на этом предположении какие-то многоэтажные модели нельзя. 3. Если пульсар нейтронная звезда, то, в соответствии с оценками и результатами наблюдений, он должен иметь диаметр порядка 10-20 км и вращаться со скоростью до 40000 оборотов в минуту. Это - очень хороший гироскоп, но его размер превышает размер реального технического устройства в 100000 раз. Какие дополнительные требования может наложить такое изменение масштаба при совершенно исключительных и неизвестных свойствах материала нейтронной звезды? Можно что-то предполагать, но что-то утверждать невозможно. 4. По существующим оценкам мощность ЭМИ пульсара превышает мощность излучения Солнца в 100 и более раз. Если эта мощность даже была бы равномерно распределена по всей небольшой поверхности пульсара нейтронной звезды, вместо концентрации в горячей точке, то и в этом случае электрическая напряженность электромагнитного поля вблизи поверхности звезды достигла бы величины порядка миллиарда вольт на метр. Известные изоляторы не выдерживают такую электрическую напряженность. В подобных условиях источник ЭМИ был бы в состоянии постоянного короткого замыкания. Тем более при концентрации излучения в области горячей точки. Последствия такого режима трудно предсказуемы. Или пространство вокруг пульсара и внутри него должно обладать свойствами, которые нам не известны, и должно выдерживать такие электрические перегрузки. 5. Для объяснения причин поляризации ЭМИ пульсара и направленности его излучения предполагается существование в пульсаре магнитного поля индукцией порядка 1012-1015 гаусс. По частной информации, она может достигать 1017 Гс.! Летом 2002 автор участвовал в работе Международной научной конференции MEGAGAUSS-9 (MG-9). Главное направление тематики конференции ясно из ее названия. Как следует из сообщений участников, магнитные поля индукцией порядка 108 Гс и сегодня остаются мечтой для исследователей вещества. Даже эксперименты с полями индукцией порядка 2107 Гс уникальны и приводят к неожиданным результатам. Какие изменения свойств вещества можно ожидать в магнитных полях на 5-9 порядков еще более интенсивных? Сегодня предположить это невозможно. Для экстраполяции же имеющихся данных достаточных оснований нет. 6. Пульсар PSR 0531-21 в Крабовидной туманности идентифицирован как маленькая звездочка 16 величины. Возникает вопрос: как нейтронная звезда диаметром порядка 10-20 км может быть оптически видима на расстоянии 4 -5 тысяч световых лет? Для этого измерительные средства должны обеспечивать разрешение порядка 10-11- 10-10 угловой секунды. Но разрешающая способность лучших современных телескопов не превышает 10-2 секунды. Если же звезда все-таки видна, то, значит, ее размеры имеют совсем другой порядок величины. 7. У некоторых пульсаров наблюдалось неоднократное дискретное изменение частоты следования импульсов на небольшую, но конечную величину. Для объяснения этого факта предполагается, что нейтронная звезда имеет твердую оболочку. Под действием механических сил оболочка ломается и формируется новая оболочка, другого радиуса. При изменении радиуса звезды должна измениться и скорость ее вращения. Расчеты на основе измеренных изменений частоты пульсаций показали [2], что радиус звезды (порядка 5-10 км) должен был измениться на 10-10 от своей первоначальной величины, т.е. на 1 микрометр! Для примера, такие относительные деформации испытывает обычное стекло под давлением порядка 5-10 Па, т.е. когда в поле тяготения Земли масса порядка 1 кг, распределена по поверхности стекла площадью один квадратный метр, лежащего на абсолютно твердом основании. Т.е. литр воды разлит на этой площади слоем толщиной 1 миллиметр! Эти цифры и их связь с механическими свойствами гипотетической твердой оболочки пульсаров вызывают вопросы, но не вызывают доверия, потому что материалы, обладающие подобными свойствами не известны. Тем более, при высокой температуре. 8. Считается, что источником энергии излучения является энергия вращения пульсара. Вот только никому пока не удается [2] разработать и предложить механизм такого энергетического преобразования! 9. Частота пульсаций некоторых пульсаров так стабильна, что даже поступили предложения о создании пульсарной шкалы времени. В таком случае, где же пульсар черпает энергию для ЭМИ в соответствии с пунктом 8? 10. Открыты пульсары, частота следования импульсов которых возрастает. Где, в таком случае (п. 8), пульсар черпает энергию? Таким образом, как говорили древние римляне, ignotum per ignotius ... Применительно к пульсарам это значит, что мы пытаемся решать не ясные проблемы, опираясь на представления, которые еще менее ясны. Принятые сегодня представления предполагают, что природа формирования периодического ЭМИ звезд типа цефеид и пульсаров не имеют ничего общего. Так ли это? Кажется, Л.А. Арцимович говорил, что природа сложна, но не злонамеренна. Мы многое в ней не знаем, и этим незнанием необходимо пользоваться аккуратно. В противном случае можно не приблизиться к истине, а безнадежно от нее уйти. Хотя представления о звездах типа цефеид и о пульсарах существенно различны, и те и другие излучают периодически изменяющиеся сигналы, те и другие могут наблюдаться визуально как обычные звезды. Это дает возможность попытаться описать их с единых позиций. Будем исходить из того, что и цефеиды, и пульсары являются обычными звездами, отличающиеся тем, что пульсируют они на различающихся модах колебаний. Что это значит? Наиболее просто сущность формы таких колебаний можно объяснять графически. На рис.1a показано подобное звезде сферическое тело, которое пульсирует на самой низкой моде - на моде нулевого порядка. Видно, что в этом случае процесс колебаний звезды характеризуется центральной симметрией нулевого порядка. Это - элементарный случай сферических колебаний. По-видимому, так и колеблются классические цефеиды и мириды. Излучение такой звезды распространяется центрально симметрично и изменяется во времени по амплитуде в соответствии с пульсациями. Сферическое тело, совершающее колебания на моде первого порядка, показано на рис. 1b. Видно, что оно разделено неподвижной центральной плоскостью. Колебания полушарий происходят относительно этой плоскости в противофазе. В пространстве излучение приобретает некоторую направленность. Его диаграмма имеет вид восьмерки максимумы которой лежат в проходящей через центр шара плоскости, нормальной к плоскости нулевых колебаний. Если пульсирующая звезда вращается вокруг произвольной оси, излучение может быть дополнительно модулировано с двойной частотой вращения. Этим можно объяснить эффект Блажко, наблюдаемый у звезд, относимых к группе звезд типа RR Лиры. Сферическое тело, совершающее колебания на моде четвертого порядка, показано на рис. 1c. В этом случае поверхность тела оказывается разделенной на площадки узловыми параллелями и меридианами, которые остаются неподвижными при колебаниях площадок. Характерно, что любые две площадки, имеющие общую границу, пульсируют в противофазе. По- видимому, так колеблются цефеиды с биениями или полипериодические цефеиды. По крайней мере, численные оценки говорят о том, что соотношение периодов Рис. 1. Формы пульсаций звезд на низких модах колебаний. a нулевая мода колебаний, b первая мода, c четвертая мода колебаний на первой, второй и третьей гармониках четвертой моды хорошо соответствует типичному соотношению периодов гармонических составляющих сигналов, поступающих к нам от известных полипериодических цефеид [1]. Каждая из площадок формирует свою диаграмму направленности излучения, что может накладывать отпечаток на результат наблюдения такой звезды при ее вращении. Пульсации любых двух площадок, имеющих общую границу, происходят в противофазе. Рис. 2. Распределение поля пульсаций звезд на моде высокого порядка. С увеличением порядка моды количество площадок, на которые поверхность сферического тела разделена, увеличится. Это видно на рис. 2, где показан один из возможных вариантов распределения поля колебаний для моды приблизительно 25 порядка. Этот рисунок несколько схематичен, поскольку распределение параллелей на нем не вполне соответствует тому, что должно следовать из присоединенной функции Лежандра. Но это не существенно при качественных оценках. Более высокая строгость в рассматриваемом приближении не окупается ценностью результата, который был бы получен не данном этапе. Важно, что на сферической поверхности тела узловые линии пересекаются, и площадки, которые сформированы ими, имеют разную форму. Количество площадок увеличивается с увеличением порядка моды. При этом возрастает и частота пульсаций. Как и прежде, любые две соседние площадки, имеющие общую границу, пульсируют в противофазе. Описанные формы колебаний следуют из решения волнового уравнения для сферического тела при абсолютно мягких граничных условиях. Уравнение рассматривалось для случая некоторой постоянной скорости звука в звезде. Это не совсем справедливо, но другого реального пути решения этой задачи (кроме цифровых вычислений) пока не существует. Решение при таких условиях позволяет получить результат, качественно отражающий основные свойства строгого решения и дающий возможность анализировать явление. Как и в предыдущем случае, при колебаниях на модах высокого порядка каждая площадка формирует свою диаграмму направленности излучения. Их, как легко представить, может быть очень много, и лучи любых двух площадок, имеющих общую границу, колеблются в противофазе. К сожалению, никто не исследовал влияние факта формирования диаграммы направленности на свойства наблюдаемого излучения звезд. Как уже отмечалось, при пульсациях звезды на моде нулевого порядка модуляция ЭМИ за счет пульсаций происходит центрально симметрично, т.е., по существу, не направленно. При колебаниях звезды на модах первого, второго низкого порядка, когда изменения радиуса поверхности звезды и, соответственно, радиуса кривизны, в пределах каждой площадки невелико, каждая площадка излучает в пределах своего угла направленности, практически определяемого только распределением ЭМИ в пределах этой площадки. При увеличении порядка моды колебаний появляется еще один важный фактор, влияющий на направленность излучения. Дело в том, что, с одной стороны, диэлектрическая проницаемость среды в звезде и в окружающем пространстве различна, а с другой при высоком номере моды колебаний кривизна поверхностей площадок может изменяться во много раз даже при относительно небольших амплитудах пульсаций. Это приводит к тому, что в процессе периодических колебаний периодически происходит фокусировка и рассеяние излучения [3, 4] , как это показано на рис. 3. Это чрезвычайно важно. Наблюдатель, если он попадает в пределы диаграммы направленности одной из площадок, воспринимает ЭМИ в виде импульсов, спектр заполнения которых охватывает весь спектр излучения звезды. Т.е. так, как это имеет место при наблюдении пульсаров. Остаются вопросы: почему в звезде возникают пульсации? Почему они возникают на определенных модах? Эти вопросы рассмотрены [5, 6] и решены. Здесь их решение не приводится, поскольку оно, хотя и не очень сложно, но довольно громоздко. Интересующихся отсылаем, например, к [5, 6, 7] . . Рис. 3. Фокусировка и рассеяние излучения звезды при ее колебаниях на моде высокого порядка Кратко результат решения выглядит так. 1. Автоколебания в звезде возникают только при условии существования в ней некоторой поверхности, на которой скорость термоядерной реакции изменяется пространственным скачком. 2. Пульсации возникают на модах низкого порядка, если сферическая поверхность разрыва лежит в области середины радиуса звезды. 3. Пульсации возникают на модах все более высокого порядка при приближении поверхности разрыва к поверхности звезды. 4. При приближении поверхности разрыва к поверхности звезды спектр заполнения импульсов смещается в сторону гамма-диапазона. 5. С увеличением номера моды частота пульсаций возрастает. Предложенный подход позволил объяснить следующие факты и зависимости. Пункты 1 и 2 относятся в звездам, пульсирующих на модах низкого порядка, остальные к пульсарам. 1. Единство природы пульсирующих звезд. 2. Эффект Блажко. 3. Природу импульсного излучения пульсаров. 4. Связь пульсаров с взрывами сверхновых. 5. Высокую частоту следования импульсов. 6. Высокую интенсивность импульсов за счет фокусировки ЭМИ. 7. Природу гигантских импульсов. 8. Природу стабильных субимпульсов. 9. Природу плавающих субимпульсов. 10. Малые девиации импульсов во времени. 11. Постоянное изменение средней частоты следования импульсов. 12. Дискретное изменение частоты следования импульсов. 13. Поляризацию излучения пульсаров. 14. Широкий спектральный состав импульсов. 15. Выключение пульсаров. 16. Влияние номера моды колебаний на степень поляризации излучения пульсирующих звезд. Косвенные признаки, такие как оцениваемая ширина диаграммы направленности излучения, некоторые особенности спектра ЭМИ, наблюдающиеся месячные циклы излучения некоторых пульсаров позволяют ориентировочно оценить их размер. Он оказывается порядка размера белого карлика, т.е. пульсар имеет диаметр порядка 50-100 тысяч километров и более. Следовательно, пульсары никак не могут быть нейтронными звездами. Если изложенные представления о пульсациях звезд верны, их можно распространить и на магнитары. Все эти результаты получены без использования представлений о незнакомых нам нейтронных звездах, без предположений о запредельных скоростях их вращения и о гигантских магнитных полях в них. В их основу легли только известные физические законы и проверенные на опыте результаты известных экспериментов и наблюдений, результаты громоздкого, но достаточно строгого теоретического анализа. Детальное развитие изложенных представлений требует дальнейшей работы, конца которой не видно. Литература. 1. Кокс Дж.П. Теория звездных пульсаций. Пер. с англ.- М.: Мир, 1983. 326 с. 2. Смит Ф.Г. Пульсары: Пер. с англ. М.: Мир,1979. 268 с. 3. Фейнмановскиe лекции по физике. Т. 3. М.: Мир, 1965. 238 с. 4. Яворский К.М., Детлаф А.А. Справочник по физике. М.: Наука, 1965. 848 с. 5. Гладышев В.Н. Автоколебания при горении и термядерных взаимодействиях. Новосибирск: НИЦ ОИГГМ СО РАН, 1999. 134 с. 6. Gladyshev V.N. About a magnetic field of a pulsar // MEGAGAUSS-9. Proceedings of Ninth International Conference on Megagauss Magnetic Field Generation and Related Topic. Moscou St.-Petersburg? July 7-14, 2002. Sarov: VNIIEF, 2004, p.p 875-881. 7. Гладышев В.Н. Является ли пульсар нейтронной звездой? // Естественные и технические науки 2006, 6, с.с. 52-58.