Аномальный магнитный момент
30.08.2001 14:16 | "Физическая Энциклопедия"/Phys.Web.Ru
Отклонение величины магнитного момента элементарной частицы
от "нормального" значения, предсказываемого релятивистским квантовомеханическим
уравнением, описывающим поведение частицы.
Магнитный момент элементарной частицы с массой m и
зарядом е представляется
в виде ![]() ,
где
,
где
[Цитировать][Ответить][Новое сообщение]
| Форумы >> Обсуждение публикаций Астронета |
| Список / Дерево Заголовки / Аннотации / Текст |
- >> Аномальный магнитный момент
( "Физическая Энциклопедия"/Phys.Web.Ru,
30.08.2001 14:16, 8.1 КБайт)
Отклонение величины магнитного момента элементарной частицы от "нормального" значения, предсказываемого релятивистским квантовомеханическим уравнением, описывающим поведение частицы.
Магнитный момент элементарной частицы с массой m и зарядом е представляется в виде
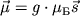 ,
где
,
где 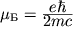 - магнетон
для рассматриваемой частицы,
- магнетон
для рассматриваемой частицы, 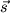 - ее спиновый
момент (в единицах
- ее спиновый
момент (в единицах
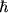 ), g - безразмерный множитель
(g-фактор), зависящий от типа
частицы. Из теоремы CPT следует,
что частица и античастица имеют одинаковые g-факторы.
Для частицы со спином 1/2 из уравнения Дирака в
пренебрежении радиационными
поправками следует, что g=2 при условии, что электромагнитное поле введено минимальным образом, т.
е. с помощью замены
), g - безразмерный множитель
(g-фактор), зависящий от типа
частицы. Из теоремы CPT следует,
что частица и античастица имеют одинаковые g-факторы.
Для частицы со спином 1/2 из уравнения Дирака в
пренебрежении радиационными
поправками следует, что g=2 при условии, что электромагнитное поле введено минимальным образом, т.
е. с помощью замены 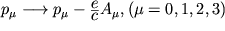 ,
где р - 4-импульс частицы, А
- четырехмерный
потенциал поля. Значение g=2 отвечает нормальному
(дираковскому) магнитному моменту частицы со спином 1/2. Аномальным магнитным моментом
называют часть, связанную
с отклонением g-фактора от 2. Эта часть целиком связана с радиационными
поправками.
,
где р - 4-импульс частицы, А
- четырехмерный
потенциал поля. Значение g=2 отвечает нормальному
(дираковскому) магнитному моменту частицы со спином 1/2. Аномальным магнитным моментом
называют часть, связанную
с отклонением g-фактора от 2. Эта часть целиком связана с радиационными
поправками.Измерения интервалов сверхтонкой структуры уровней энергии водорода и дейтерия, выполненные в 1947 Дж.Нафе (J.E.Nafe), Э. Нельсоном (Е.В.Nelson) и И. Раби (I.I.Rabi), показали отклонения от теории, в которой использовалось значение g=2 для электрона. Для объяснения этого отклонения Г. Брейт (G.Breit) в 1947 предположил наличие малой - аномальной - поправки к дираковскому значению g-фактора. В 1948 П.Куш (P.Kusch) и Г.Фоли (H.Foley) выполнили прямые измерения g-фактора электрона, подтвердившие предположение Брейта, В этом же году Ю.Швингер (J.Schwinger) показал, что радиационная поправка низшего порядка по постоянной тонкой структуры
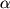 в рамках квантовой
электродинамики
(КЭД) приводит к значению
в рамках квантовой
электродинамики
(КЭД) приводит к значению 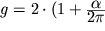 ,
хорошо согласующемуся с измеренным.
,
хорошо согласующемуся с измеренным.Аномальный магнитный момент частицы со спином 1/2 удобно выражать через т. н. аномалию
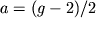 .
Измерения аномалии для лептонов
- электрона (е-),
позитрона (е+),
положительно и отрицательно заряженных мюонов
(
.
Измерения аномалии для лептонов
- электрона (е-),
позитрона (е+),
положительно и отрицательно заряженных мюонов
(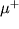 и
и 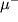 ) относятся к числу наиболее точных измерений
в физике. Проведены расчеты вклада в
) относятся к числу наиболее точных измерений
в физике. Проведены расчеты вклада в 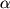 высших радиационных
поправок порядка
высших радиационных
поправок порядка 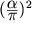 и
и 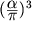 , в т.
ч. адронной поляризации
вакуума и слабого
взаимодействия; заканчиваются расчеты поправки порядка
, в т.
ч. адронной поляризации
вакуума и слабого
взаимодействия; заканчиваются расчеты поправки порядка 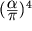 для электрона. Соответствующие экспериментальные и
теоретические
значения хорошо согласуются:
для электрона. Соответствующие экспериментальные и
теоретические
значения хорошо согласуются:
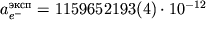 ,
,
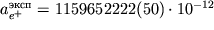
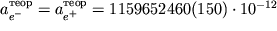
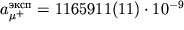
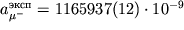
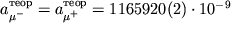
Это подтверждает справедливость КЭД и теоремы CPT. [Теоретические расчеты выполнены при значении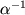 = 137,035963(15).]
= 137,035963(15).]Для частицы со спином 1 нормальному магнитному моменту отвечает значение g=1, поскольку такое значение g-фактора следует из уравнения Прока при минимальном включении электромагнитного поля. При этом аномальный магнитный момент связан с отклонением g-фактора от единицы. Указанное разделение магнитного момента частицы со спином 1 на нормальную и аномальную части встречается в литературе, но не является общепринятым. В теории электрослабого взаимодействия Вайнберга-Глэшоу-Салама для W-бозона g=2.
Для адронов аномальный магнитный момент и нормальный магнитный момент имеют, вообще говоря, одинаковый порядок величины, поэтому часто оказывается неудобным разделять полный магнитный момент на нормальную и аномальную части.