Лекция 3. Определение расстояний до звёздных объектов
3.2 Средние (вековые) параллаксы
В описываемом методе для определения средних параллаксов звёзд используется движение Солнца относительно этих звёзд. Измеряя видимые смещения звёзд, вызванные этим движением, можно определить расстояние до последних, так как угловые смещения звёзд пропорциональны их расстояниям от Солнца.
Недостатком метода является то, что кроме движения, являющегося отражением движения Солнца, звёзды имеют свои, так называемые "пекулярные" (остаточные) движения, которые необходимо отделять от параллактического движения. При этом приходится вводить предположение, что пекулярные движения являются хаотическими, что, как мы увидим в последующих лекциях, не всегда выполняется.
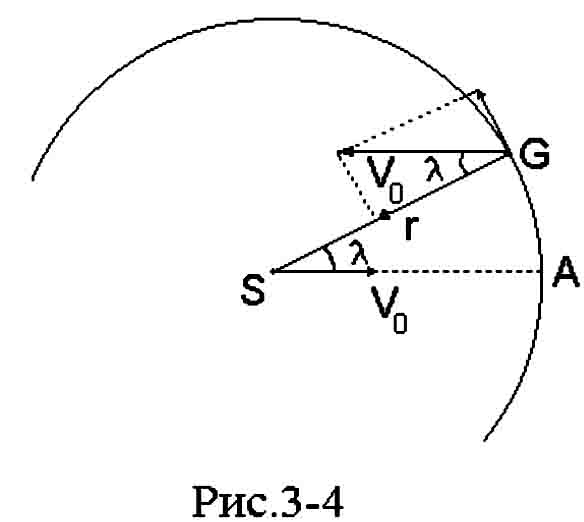 Пусть звезда G находится на расстоянии r = π-1 от Солнца (см. рис.3-4), двигающегося со скоростью V0 в направлении своего апекса A. Пусть V обозначает пространственную скорость звезды относительно Солнца. Мы можем записать:
Пусть звезда G находится на расстоянии r = π-1 от Солнца (см. рис.3-4), двигающегося со скоростью V0 в направлении своего апекса A. Пусть V обозначает пространственную скорость звезды относительно Солнца. Мы можем записать:
| V = VS + V0 |

|

|
Указанный метод хорошо послужил астрономам в ХХ веке, и не устарел в настоящее время. Дело в том, что определение абсолютных звёздных величин одним методом не дает полной уверенности, что мы не заметили какой-либо систематической ошибки в наблюдательных данных или методике их использования, так что сравнение результатов, полученных разными методами, повышает надежность оценок. Вместе с тем следует отметить, что применение кинематических методов определения расстояний до звёзд требует высокой однородности кинематических свойств используемых звёзд, что даже в окрестностях Солнца выполняется плохо.
|
Публикации с ключевыми словами:
звездная астрономия
Публикации со словами: звездная астрономия | |
См. также:
Все публикации на ту же тему >> | |