Сверхсветовое разбегание галактик и горизонты Вселенной: путаница в тонкостях
Сергей Попов
(А. Гуницкий)
Введение
В Природе очень много удивительного, и пытаться выделить самое-самое занятие неблагодарное. Кто-то полагает, что Жизнь - самое удивительное в Природе. Кто-то - что Разум. Если обратиться к неживой природе, то кто-то скажет об удивительных законах микромира, кто-то о процессах самоорганизации и хаосе. Но, наверное, если составлять список, то всегда в десятку самых удивительных феноменов будет попадать расширение Вселенной.
Мы не будем здесь обсуждать обоснованность выводов о расширении Вселенной на основе космологических наблюдений. Равно, мы не будем обсуждать основы специальной и общей теорий относительности (СТО и ОТО). Если оставить в стороне вопрос о "самом начале", которые нас здесь не будет существенно занимать (мы будем полагать под "началом" достаточно далекий момент времени - скажем, до первичного нуклеосинтеза - чтобы не вдаваться в спекуляции об очень ранней Вселенной, если угодно, то можно полагать "началом" - момент окончания инфляционной стадии, если она была), то сомнений в данных о расширении Вселенной нет, как нет больших сомнений в применимости ОТО в этом случае (всякие возможные эффекты квантовой гравитации и т.п. тут неважны). Мы будем обсуждать стандартную картину, следуя в основном недавней статье Тамары Дэвис (Tamara M. Davis) и Чарльза Лайнвивера (Charles H. Lineweaver) "Expanding confusion: common misconceptions of cosmological horizons and the superluminal expansion of the universe" и книге Эдварда Гаррисона (Edward Harrison) "Cosmology: the science of the universe". Стоит также упомянуть работы Кианга - T. Kiang - "Time, Distance, Velocity, Redshift: a personal guided tour", "Can We Observe Galaxies that Recede Faster than Light ? - A More Clear-Cut Answer". Кроме того, обсуждаемые вопросы разобраны во многих учебниках и монографиях по космологии.
Тонкие детали
(А. Гуницкий)
Расширение Вселенной (мы будем писать Вселенную с большой буквы, хотя речь идет именно о наблюдаемом мире, который иногда пишут с маленькой буквы) является очень странным процессом, осмысление которого во-первых вызывает определенный интеллектуальный дискомфорт, во-вторых приводит к некоторой путанице. Безусловно, путаница в головах не относится к профессиональным космологам и тем, кто серьезно разбирался с этими вопросами (в стандартных учебниках по космологии все обычно аккуратно расписано). Однако, в популярной литературе неточности присутствуют в избытке. Дэвис и Лайнвивер, ни в коей мере не претендуя на открытие нового феномена, попытались обсудить основные неточности, связанные с популярным (и не только) изложением некоторых деталей, связанных с расширением Вселенной, и на наш взгляд им это удалось. Так что их работа носит скорее просветительско-педагогический характер. В приложении к своей статье они приводят цитаты из известных книг известных людей, где в той или иной степени неточно описаны эти детали (не относя себя к числу великих, нельзя не отметить, что и мы в свое время внесли вклад в распространение путанных знаний, о чем весьма сожалеем). Забегая вперед скажем, что основным источником путаницы является использование формулы для релятивистского эффекта Доплера там, где ее применять нельзя.
Обсудим две детали: сверхсветовое расширение (когда скорость удаления галактики превышает световую) и горизонты. В этом нам будут помогать рисунки из статьи Дэвис и Лайнвивера.
Теоретическое введение
В начале немного пояснений.
Будем использовать метрику Робертсона-Уокера в упрощенном варианте:
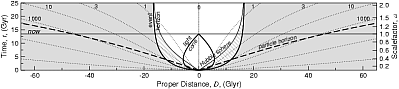
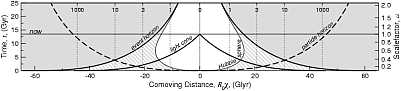
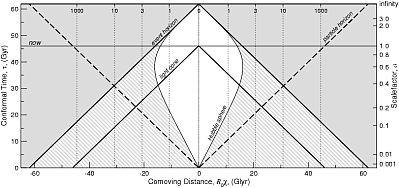
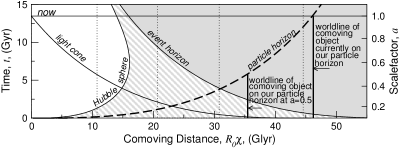
Наряду с обычным временем эти величины использованы для построения рисунков внизу. По вертикальной оси отложено время, по горизонтальной - расстояние. Мировые линии "галактик" отмечены пунктиром. Они пронумерованы красным смещением в настоящий момент времени (в космологии красное смещение связано не со скоростью напрямую, оно определяется формулой: 1+z=R(t0)/R(t), обратите внимание, красное смещение данного объекта изменяется со временем, в разных моделях оно может как расти так и уменьшаться). "Нам" соответствует линия χ=0 (и, разумеется, D=0). Как видно на втором (1б) и третьем (1в) рисунках, при использовании сопутствующего расстояния мировые линии всех "галактик" являются прямыми линиями. На первом рисунке (1а) видно расширение Вселенной: мировые линии "галактик" удаляются от нас - собственное расстояние растет.
Напомним, что постоянная Хаббла является величиной, изменяющейся со временем. Она равна отношению производной масштабного фактора по времени к самому масштабному фактору: H=(dR/dt)/R. Скорость убегания определяется как производная собственного расстояния:
В космологии бывает опасно применять СТО (и интуицию на ее основе), т.к. это может приводить к ошибочным выводам (Кианг называет это "тени СТО"). Дело в том, что скорость убегания существенно отличается от привычного нам понятия скорости. Для нее СТО неприменима "в лоб". Скорость убегания является не свойством источника, а свойством точки в пространстве. Поэтому не следует ждать прямой применимости понятий, интуитивно наработанных в СТО, к космологии.
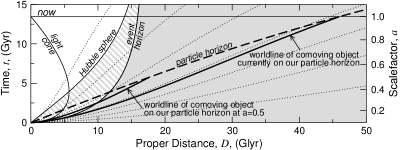
Очевидно, что есть расстояние - сфера Хаббла, DH, - на котором скорость убегания равна скорости света. Причем, как будет показано ниже, мы можем видет эти объекты (конечно, нужно учесть, что свету нужно время - и довольно большое - чтобы добраться до нас от этих объектов). Это удивительный факт ни чему не противоречит (в том числе и СТО, которую тут просто нельзя применять).
Сверхсветовое расширение
(А. Гуницкий)
Обсудим возможность наблюдения "сверхсветовых галактик". В начале поговорим о световом конусе. Импульс света от источника может достигнуть нас, если источник в момент излучения лежит внутри светового конуса (если он лежит на световом конусе, то мы видим его сейчас, если внутри - то мы видели его раньше). В "нормальных" координатах (верхний рисунок) световой конус превращается в каплеобразную фигуру. Это связано с расширением Вселенной. Если мы мысленно пойдем по световому лучу, пришедшему к нам от далекой галактики, назад по времени (на рисунке это движение вниз), то собственное расстояние (и сопутствующее) до этой галактики будет, естественно, уменьшаться. В начале оба расстояния от нашей Галактики будут увеличиваться (это пока нормально, мы же "уходим" от нашей Галактики), но потом картина для собственного расстояния начнет изменяться: сопутствующее расстояние будет увеличиваться, а вот собственное начнет уменьшаться . Движение в прошлое соответствует сжатию Вселенной, собственное расстояние (D=R(χ1 - χ2)) между двумя точками с заданными сопутствующими координатами (χ1 и χ2) будет уменьшаться за счет уменьшения масштабного фактора R(t). Поэтому и световой конус на рис 1а будет "закругляться" (более крупно это видно на рисунке 2а). На рисунке 1в (где по вертикальной оси отложено конформное время) световой конус ведет себя привычным образом (предоставляем читателю самому с этим разобраться), и ясно видно, что обычная логика имеет место - на больших красных смещениях мы видим сейчас объекты с более далеким сопутствующим расстоянием (а значит, в настоящий момент эти объекты дальше от нас, чем объекты с меньшими z).
Теперь посмотрим, как ведет себя Хаббловская сфера. Здесь все привычно, в "нормальных" координатах она уменьшается при движении в прошлое. Однако, при перерисовывании в сопутствующих координатах картина меняется (и это помогает прояснить смысл происходящего). Если мы используем сопутствующее расстояние, то хаббловская сфера ведет себя немонотонно! На третьем рисунке (1в) ясно видно, что для данной конкретной модели (30/70) источники могут попадать в Хаббловскую сферу, а потом выходить из нее.
И вот - самое интересное. Как хорошо видно, на нашем световом конусе есть источники, которые и в момент излучения, и в настоящий момент находятся за пределами нашей Хаббловской сферы, т.е. их скорость убегания выше световой и в момент испускания, и сейчас. Для модели 30/70 все источники с z>1.46 в настоящий момент удаляются от нас быстрее скорости света. В модели с замедлением расширения из факта превышения скорости света в настоящий момент автоматически следует превышение и в момент испускания излучения.
Как это может быть? Вообще говоря, то, что мы сейчас видим испущенный давным давно свет, а сами источники сейчас удаляются от нас со сверхсветовой скоростью, не должно вызывать удивления. Более интересно то, что мы также видим свет источников, которые в момент излучения имели скорость убегания больше световой, а свет от них все равно к нам попал. Попробуем это прояснить и будем использовать для наглядности сферу Хаббла. Здесь важно сравнить две вещи: как в данный момент времени ведет себя Хаббловская сфера (скорость ее расширения, dDH/dt) и скорость убегания фотона (Vrec -c). Если dDH/dt > Vrec -c, то фотон рано или поздно попадет внутрь Хаббловской сферы и сможет достичь нас. Т.е. важно понять, положительна или отрицательна скорость фотона относительно границы сферы Хаббла. Обратите внимание (рис 1а и 2а), что собственное расстояние от нас до фотона, двигающегося по нашему световому конусу, увеличивается пока фотон находится вне сферы Хаббла, и уменьшается внутри нее.
Мы посвятили столько времени разбору сферы Хаббла не потому, что это какое-то очень важное построение - можно прекрасно обойтись вообще без введения этого понятия. Например, до нас доходят (дошли или дойдут) фотоны, которые были испущены внутри светового конуса, проведенного из нашего бесконечного будущего. Чтобы это понять и объяснить никакая сфера Хаббла не нужна. Однако, "джинн уже выпущен из бутылки": сфера Хаббла, как расстояние, на котором скорость убегания равна скорости света, прочно вошла в популярную литературу. А потому важно понимать "что это за зверь".
Типичная путаница со сверхсветовыми скоростями убегания и возможностью наблюдения таких источников связана с тем, что используют формулу для релятивистского эффекта Доплера, в которой стремление красного смещения к бесконечности соответствует стремлению скорости к скорости света. Т.о., говорят, следуя этому заблуждению: "наблюдать галактики, убегающие со скоростью больше световой, нельзя, т.к. они находятся за горизонтом". На самом деле они находятся за сферой Хаббла, которая не является горизонтом, а потому их можно прекрасно наблюдать. В некоторых моделях горизонт и сфера Хаббла могут совпадать, но, по всей видимости, мы живем во Вселенной, где горизонт шире сферы Хаббла.
Красное смещение позволяет определить не скорость, а сопутствующее расстояние (если задана модель). Сопутствующее расстояние, χ, как функция z задается произведением (c/R0) на интеграл от нуля до z, под интегралом стоит dz'/H(z'). В ряде космологических моделей бесконечное красное смещение будет соответствовать бесконечному сопутствующему расстоянию. В модели 30/70 бесконечное красное смещение соответствует объекту на горизонте частиц с конечным сопутствующим расстоянием от нас. Как легко понять нулевое значение масштабного фактора в момент излучения будет давать бесконечное красное смещение, т.е. это соответствует источнику на t=0 (R(t=0)=0).
Отметим также (см. рис), что расстояние до далеких объектов нельзя оценивать, умножая скорость света на {(возраст Вселенной сейчас)-(возраст Вселенной в момент излучения)}. Собственное расстояние существенно выше. Часто можно прочесть, что "т.к. возраст Вселенной порядка 13 миллиардов лет, то расстояние до самых далеких из наблюдаемых галактик порядка 12 миллиардов световых лет". Это неверно. Например, расстояние до объекта с z=10 в модели, приведенной на рисунках, будет около 30 миллиардов световых лет (расстояние же между нами в момент излучения было гораздо меньше, и составляло несколько миллиардов световых лет). Обратите внимание на масштаб шкалы для самых больших расстояний на Карте Вселенной.
Обычная же интуиция применима на малых расстояниях. Примерно до z=0.1 результаты по выписанным выше формулам и по эффекту Доплера будут близки друг к другу. Также для таких близких источников можно оценивать расстояния умножая скорость света на {(возраст Вселенной сейчас)-(возраст Вселенной в момент излучения)}.
Горизонты
(А. Гуницкий)
С горизонтами большой путаницы в литературе нет. Просто полезно разобраться. Рассмотрим два важных горизонта: горизонт частиц и горизонт событий.
Горизонт частиц - это расстояние до самого далекого источника, в принципе наблюдаемого в данный момент времени (на всякий случай уточним, что речь идет о расстоянии до объекта в момент приема фотона, а не в момент излучения). Иногда этот радиус определяют по-другому: расстояние, которое фотон может пройти от t=0 до данного момента (т.е. это расстояние, на которое можно передать информацию за время, равное возрасту Вселенной). Из рис. 1в хорошо видно, что оба определения эквивалентны. В нерасширяющейся Вселенной конечного возраста (т.е. с "началом") этот радиус линейно рос бы со временем. Во Вселенной, расширяющейся с замедлением, радиус рос бы всегда, но медленнее. В ускоряющейся Вселенной радиус стремится к конечному значению (в сопутствующих координатах) при стремлении времени к бесконечности (т.е. есть объекты, которые мы никогда не увидим, сколько бы ни ждали). Этот горизонт нельзя определить как скорость света, умноженную на время после начала расширения. Сопутствующая координата объекта на горизонте частиц в момент t определяется как скорость света, умноженная на интерграл от 0 до данного времени t, под интегралом стоит dt'/R(t') - конформное время. Соответственно, для определения собственного расстояния надо потом умножить результат на масштабный фактор в данный момент. Обратите внимание, красное смещение источников на горизонте частиц бесконечно.
На рисунках горизонт частиц проиллюстрирован световым конусом из точки t=0, χ=0 в будущее. Однако, этот конус сам по себе не является горизонтом частиц! В каждый данный момент ti горизонт является сечением этого конуса плоскостью t=ti. Т.е. это трехмерная сфера вокруг нас, которая изменяется с течением времени. Зато нарисованный конус позволяет увидеть, как горизонт частиц изменяется со временем (в частности, как "галактики" входят в него, т.е. становятся видимыми для нас).
Горизонт событий - довольно хитрое понятие (и не во всякой космологической модели он существует). Давайте еще раз посмотрим на рис. 1в. Кроме нашего светового конуса (для настоящего момента времени), мы видим световой конус для момента в бесконечном будущем - это и есть горизонт событий. Он делить плоскость (пространство-время) на две части. События внутри конуса (напомним, что точка на этой плоскости - это именно событие в пространстве И времени) делятся на две группы. Те, что находятся внутри конуса или были доступны нам для наблюдения в прошлом, или же будут доступны в будущем. События вне конуса нам принципиально недоступны для наблюдений.
Обратите внимание, что в модели 30/70 бесконечному будущему соответствует конечное конформное время.
Попробуем дать некоторое дополнение/пояснение про горизонт событий. Расстояние до горизонта событий в настоящий момент - это расстояние до частицы, до которой может дойти наш световой сигнал, посланный в данный момент. На рис. 1в видно, что, если мы продолжим наш световой конус в будущее, то он попадет на верхнюю горизонталь в точке, которая находится на таком же сопутствующем расстоянии, на каком конус из бесконечного будущего пересекает нашу горизонталь ("now"). Или можно сказать так: световой конус частицы на горизонте событий пересечет нашу мировую линию в бесконечном будущем.
На рисунке 2б видно, что для сопутствующего расстояния горизонт событий сокращается. И это понятно. Во Вселенной, которая расширятся ускоренно, со временем сигналу все "труднее и труднее" добраться до далеких галактик - они удаляются слишком быстро (а будут еще быстрее). Сопутствующее расстояние до частицы на этом горизонте определяется как произведение скорости света на интеграл от данного момента времени до "конца" (до бесконечности), под интегралом, как и выше, dt'/R(t').
Заключение
(А. Гуницкий)
Выше мы постарались прояснить некоторые тонкие моменты, связанные с расширением Вселенной. Мы можем наблюдать (и наблюдаем) источники, которые и в момент излучения, и сейчас имеют скорость убегания, превышающую скорость света. Расстояния до далеких объектов превышают произведение скорости света и возраста Вселенной. Расстояние, на котором скорость убегания сравнивается со световой, не является горизонтом (т.е. границей видимой части Вселенной), и вообще не является физически выделенным расстоянием (объекты прямо перед этой границей и прямо за ней ничем не отличаются принципиально, как не отличаются и условия их наблюдений). Горизонтом наблюдаемой Вселенной является горизонт частиц, на нем источники имеют бесконечные красные смещения.
Выражаю глубокую признательность С.Блинникову, П.Иванову, М.Прохорову за ряд ценнейших замечаний.
|
Публикации с ключевыми словами:
Космология - Расширение Вселенной
Публикации со словами: Космология - Расширение Вселенной | |
См. также:
Все публикации на ту же тему >> | |