po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Razmernosti i podobie astrofizicheskih velichin << § 6.4 Chislennoe modelirovanie vspyshek i kollapsa zvezd | Oglavlenie | § 7.2 Vremya relaksacii zvezdnyh sistem >>

Glava VII. Analiz razmernostei i chislennoe modelirovanie zvezdnyh sistem

Teoriya analiza razmernostei i podobiya mozhet primenyat'sya i v zvezdnoi astronomii, zanimayusheisya izucheniem dinamiki zvezdnyh sistem. Nekotorye zadachi na primenenie metodov analiza razmernostei k zvezdnym sistemam byli rassmotreny v gl. 2. Zdes' my bolee podrobno rassmotrim metody analiza razmernostei i osobenno chislennoe modelirovanie primenitel'no k zvezdnym sistemam, rassmatrivaemym kak skoplenie material'nyh tochek, dvizhushihsya pod deistviem vzaimnogo gravitacionnogo prityazheniya. Stolknoveniyami zvezd budem prenebregat'. Kak i v predydushih glavah, my ne pretenduem na polnoe izlozhenie teorii zvezdnyh sistem, osnovnoe vnimanie udeleno voprosam analiza razmernostei i chislennomu modelirovaniyu.

§ 7.1 Sistema uravnenii i parametry zvezdnyh sistem

Terminom "zvezdnaya sistema" mozhno oboznachat' skopleniya zvezd s samym razlichnym ih chislom - ot neskol'kih zvezd v kratnyh sistemah do galaktik s sotnyami milliardov zvezd. K zvezdnym sistemam mozhno otnesti i skopleniya galaktik. Obshim dlya vseh etih sistem yavlyaetsya to, chto ih stroenie i evolyuciya opredelyayutsya tol'ko silami vzaimnogo gravitacionnogo prityazheniya. Osnovnaya sistema uravnenii, opisyvayushaya takie ob'ekty, est'

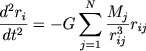
$\frac{d^{2}r_{i}}{dt^{2}}= - G \sum\limits_{j=1}^{N} \frac{M_{j}}{r^{3}_{ij}} r_{ij}$ (7.1)

Zdes' r_i - radius vektor i zvezdy (ili galaktiki), M_i - ee massa, r_ij=r_i-r_j, N - chislo zvezd ili galaktik v sisteme. Analizom sledstvii, vytekayushih iz uravnenii (7.1), i metodov ih chislennogo resheniya my i budem zanimat'sya.

Dlya etogo nam budet udobnee vse mnogoobrazie zvezdnyh sistem razbit' na dve osnovnye gruppy:

1. Zvezdnye sistemy, sostoyashie iz otnositel'no nebol'shogo chisla zvezd (N ≈ 10-10⁵). K nim otnosyatsya galakticheskie skopleniya i skopleniya galaktik. Forma takih sistem bolee ili menee sferichna, zametnogo vrasheniya u nih net. Vpred' my budem nazyvat' takie sistemy prosto skopleniyami, schitat' ih sferichnymi i predpolagat',chto oni ne vrashayutsya.

2. 1.Spiral'nye galaktiki, pokazyvayushie ochen' uploshennuyu strukturu (tolshina v 10-20 raz men'she diametra). Takie sistemy bystro vrashayutsya, no samo vrashenie neodnorodno (netverdotel'no). Chislo zvezd v spiral'nyh galaktikah N ≈ 10¹⁰-10¹². V dal'neishem takie sistemy, kotorye my budem nazyvat' prosto galaktikami, budut schitat'sya ochen' ploskimi i bystro vrashayushimisya, tak chto ih struktura v pervuyu ochered' opredelyaetsya imenno usloviyami vrasheniya.

Razumeetsya, etimi dvumya gruppami otnyud' ne ischerpyvaetsya raznoobrazie zvezdnyh sistem. Est' ellipticheskie galaktiki, v tom chisle i sfericheskoi formy, bez zametnogo vrasheniya, no imeyushie 10¹⁰ i bolee zvezd. Ochen' raznoobrazny geometricheskie formy galakticheskih skoplenii. Izvestny sluchai sistem negravitacionno vzaimodeistvuyushih galaktik. Dazhe sil'no uploshennye spiral'nye galaktiki sostoyat iz podsistem, v chislo kotoryh vhodyat promezhutochnye i sfericheskie podsistemy. Razumeetsya, vse eti osobennosti takzhe nuzhdayutsya v teoreticheskoi interpretacii.

Odnako, eshe raz podcherkivaem, s tochki zreniya issledovaniya obshih svoistv zvezdnyh sistem na osnove teorii analiza razmernostei i podobiya i dlya postanovki chislennogo modelirovaniya zvezdnyh sistem dostatochno rassmotret' dva ih tipa - kvazisfericheskie nevrashayushiesya sistemy s otnositel'no nebol'shim chislom zvezd i bystro vrashayushiesya ploskie galaktiki s ochen' bol'shim chislom zvezd.

Zvezdnye sistemy my budem harakterizovat' ih polnoi massoi

$\mathcal M = \sum\limits_{i=1}^{N} M_{i} = N \overline{M}$ (7.2)

gde $\overline{M}$ - srednyaya massa zvezdy. Strogo govorya, dinamika zvezdnyh sistem zavisit i ot raspredeleniya zvezd po massam. Pust' f(M)dM - normirovannoe na N chislo zvezd v skoplenii s massami ot M do M+dM. Togda

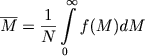
$\overline{M} = \frac{1}{N} \int\limits_{0}^{\infty} f(M)dM$ (7.3)

Vo mnogih sluchayah my ne budem uchityvat' razlichie mass zvezd. Togda my budem schitat' vse zvezdy imeyushimi odinakovuyu massu $\overline{M}$ . No v nekotoryh zadachah uchet funkcii f(M) obyazatelen. Vtorym vazhnym parametrom yavlyaetsya radius sistemy R. Prostranstvennoe raspredelenie zvezd v zvezdnyh sistemah, kak pravilo, neodnorodno. Chasto imeet mesto koncentraciya zvezd k centru. Tem ne menee mozhno vesti srednyuyu koncentraciyu zvezd - ob'emnuyu (srednee chislo zvezd v edinice ob'ema) dlya skoplenii i poverhnostnuyu (srednee chislo zvezd na edinicu poverhnosti) v galaktikah. Imeem dlya srednei ob'emnoi koncentracii

$\overline{n} = \frac{3N}{4 \pi R^{3}}$ (7.4)

i dlya srednei poverhnostnoi koncentracii

$\overline{n_{S}} = \frac{N}{\pi R^{2}}$ (7.5)

Takzhe ne odnorodno i vrashenie galaktik, i zdes' mozhno vvesti parametr $\overline{\Omega}$ - srednyuyu uglovuyu skorost' vrasheniya. V nevrashayushihsya zvezdnyh sistemah parametra Ω net, no udobno vvesti parametr harakternogo vremeni peresecheniya odnoi zvezdoi vsego skopleniya, oboznachaemyi v dal'neishem cherez P. Dobavlyaya ko vsem razmernym parametram i bezrazmernyi parametr N - chislo zvezd v skoplenii, imeem sleduyushie nabory harakternyh parametrov zvezdnyh sistem:

1. Skopleniya

$G, \mathcal{M}, R, \overline{n}, P, N$ (7.6)

2. Galaktiki

$G, \mathcal{M}, R, \overline{n_{S}}, \Omega, N$ (7.7)

Zdes' tol'ko $\overline{n}$ i $\overline{n_{S}}$ mogut byt' vyrazheny cherez kombinacii drugih parametrov.

Iz kombinacii nezavisimyh razmernyh parametrov (7.6) i (7.7) mogut byt' sostavleny tol'ko po odnomu bezrazmernomu kompleksu. Imeem matricu razmernosti dlya skoplenii:

$\begin{matrix} \, & [G] & [\mathcal{M}] & [R] & [P] \\ \mbox{g}&-1&1&0&0 \\ \mbox{sm}&3&0&1&0 \\ \mbox{sek}&-2&0&0&1 \end{matrix}$

Otsyuda sleduet bezrazmernyi kompleks

$\Pi = (G \mathcal{M})^{1/2} R^{-3/2} P \approx (G \overline{Mn})^{1/2} P$ (7.8)

Matrica razmernosti dlya galaktik imeet vid

$\begin{matrix} \, & [G] & [\mathcal{M}] & [R] & [\Omega] \\ \mbox{g} & -1 & 1 & 0 & 0 \\ \mbox{sm} & 3 & 0 & 1 & 0 \\ \mbox{sek}&-2 & 0 & 0 & -1 \end{matrix}$

Ei sootvetstvuet bezrazmernyi kompleks

$\Pi = (G \mathcal{M})^{1/2} R^{-3/2} \overline{\Omega}^{-1}$ (7.9)

Kak obychno, chislennye znacheniya bezrazmernyh kompleksov metodami teorii razmernosti ne opredelyayutsya, no iz togo fakta, chto imeetsya lish' po odnomu bezrazmernomu kompleksu, sleduet, chto v pervom priblizhenii velichiny Π dolzhny byt' poryadka edinicy. Strogo govorya, bezrazmernye kompleksy Π, opredelennye formulami (7.8) i (7.9), dolzhny v pervuyu ochered' zaviset' ot geometrii sistemy i lish' sushestvenno slabee ot chisla zvezd v etoi sisteme. Chtoby v etom ubedit'sya, ispol'zuem metody teorii podobiya.

Vvedem v (7.1) bezrazmernye peremennye posredstvom zameny

$r_{i} = R \xi_{i}, \quad M_{i}=q_{i}\overline{M}=q_{i} \frac{\mathcal{M}}{N}$ (7.10)

a takzhe

$t=P\tau, \quad \mbox{ili} \quad t=\frac{\tau}{\overline{\Omega}}$ (7.11)

dlya skoplenii galaktik ili galaktik sootvetstvenno. Togda sistema (7.1) priobretet vid

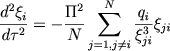
$\frac{d^{2}\xi_{i}}{d\tau^{2}} = - \frac{\Pi^{2}}{N} \sum\limits_{j=1, j \ne i}^{N} \frac{q_{i}}{\xi_{ji}^{3}}\xi_{ji}$ (7.12)

gde ξ_ji = ξ_j - ξ_i. Chislo chlenov v pravyh chastyah kazhdogo iz uravnenii sistemy (7.12) ravno N-1. Poetomu rassmatrivat' podobnye po strukture (naprimer, s odinakovoi koncentraciei k centru sfericheskie skopleniya), no sostoyashie iz raznogo chisla zvezd sistemy, to pravye chasti uravnenii (7.12) priblizhenno ravny parametru Π², umnozhennomu na srednee znachenie bezrazmernoi velichiny q_i/ξ_ji², kotoroe lish' v slaboi stepeni zavisit ot polnogo chisla zvezd v skoplenii.

Takim obrazom, ogranichivayas' dvumya klassami zvezdnyh sistem - kvazicfericheekimi nevrashayushimisya zvezdnymi skopleniyami i ploskimi vrashayushimisya galaktikami - i predpolagaya ih geometricheskoe podobie, my mozhem schitat', chto nezavisimo ot chisla zvezd v sisteme bezrazmernye kompleksy Π dolzhny byt' odinakovymi dlya kazhdogo klassa sistem. Po smyslu opredeleniya bezrazmernyh peremennyh (7.10) i (7.11) velichiny q_i, ξ_i i τ dolzhny byt' poryadka edinicy. Poetomu i bezrazmernye kompleksy Π dolzhny byt' poryadka edinicy. Itak, vremya peresecheniya zvezdoi kvazisfericheskogo skopleniya po ego diametru ravno

$P \approx \frac{R^{3/2}}{(G\mathcal{M})^{1/2}} \approx (G\overline{Mn})^{-1/2}$ (7.13)

Srednyaya uglovaya skorost' vrasheniya ploskoi galaktiki

$\overline{\Omega} \approx \frac{(G\mathcal{M})^{1/2}}{R^{3/2}} \approx (G\overline{M}\frac{\overline{n_{S}}}{R})^{1/2}$ (7.14)

Sootnoshenie tipa (7.14) mozhno neskol'ko obobshit', ispol'zuya dlya ego opredeleniya izmeneniya uglovoi skorosti s uvelicheniem rasstoyaniya ot centra galaktiki. Oboznachaya cherez M(r) massu galaktiki, zaklyuchennoi vnutri cilindra rabiusa r (i s vysotoi, ravnoi tolshine galaktiki), poluchim dlya uglovoi skorosti na etom rasstoyanii

$\Omega (r) \approx G^{1/2} \left( \frac{M(r)}{r^{3}} \right)^{1/2}$ (7.15)

S drugoi storony, sootnoshenie (7.14) mozhno proverit' po statisticheskoi svyazi mezhdu uglovoi skorost'yu i razmerom galaktik (ris. 25), poskol'ku, kak mozhno predpolagat', dispersiya mass galaktik, veroyatno, ne slishkom velika.

Vrashenie zvezdnyh sistem (a sledovatel'no, i svyazannoe s nim raspredelenie massy) opredelyaetsya nachal'noi evolyuciei sistemy i, s tochki zreniya chislennogo eksperimenta, dolzhno zadavat'sya kak nachal'noe uslovie zadachi. Estestvenno, chto pri etom prihoditsya v osnovnom ishodit' iz nablyudatel'nyh dannyh. Kak dlya nashei Galaktiki, tak i dlya ryada drugih spiral'nyh galaktik byli polucheny detal'nye raspredeleniya uglovyh skorostei i mass v ploskosti diska. Imeyutsya i statisticheskie dannye.

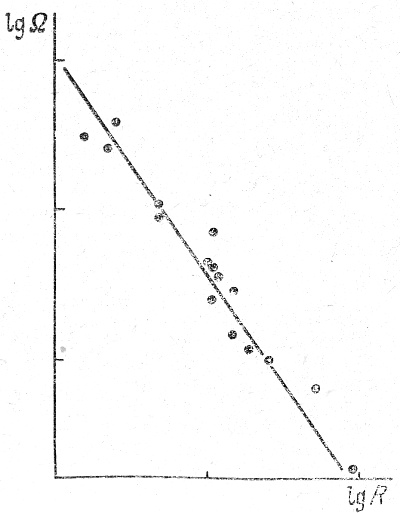
Ris. 25. Zavisimost' mezhdu uglovoi skorost'yu vrasheniya galaktik i ih razmerom.
Pryamaya liniya sootvetstvuet zavisimosti Ω ∼ R^-3/2

Naprimer, na ris. 26 privedeny statisticheskie zavisimosti mezhdu massoi galaktiki $\mathcal{M}$ i ee momentom vrasheniya $\mathfrak{M}$ ili kineticheskoi energiei vrasheniya W [1]. Pryamaya liniya sootvetstvuet empiricheskoi formule

$\mathfrak{M} \sim \mathcal{M} R^{2} \Omega \sim \mathcal{M}^{7/4}$ (7.16)

V rabote [2] bylo naideno, chto bezrazmernyi kompleks

$\Pi^{\prime} = W \mathfrak{R}^{2} G^{-2} \mathcal{M}^{-5}$ (7.17)

obladaet bolee slaboi zavisimost'yu ot geometrii sistemy i raspredeleniya mass vnutri sistemy.

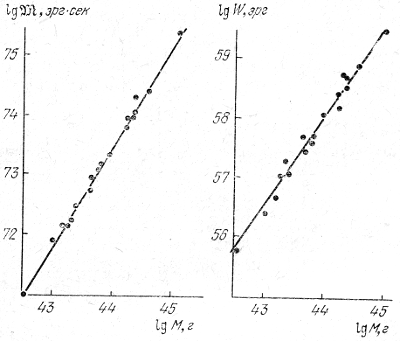
Ris. 26. Zavisimost' mezhdu vrashatel'nym momentom $\mathfrak{M}$ i massoi $\mathcal{M}$ (sleva) i mezhdu energiei vrasheniya W i massoi $\mathcal{M}$ (sprava) dlya spiral'nyh galaktik.

Issledovaniyu vrasheniya zvezdnyh sistem bylo posvyashen ochen' mnogo rabot, no poskol'ku uverennyh obshih sootnoshenii poka net, v chislennyh eksperimentah obychno vybirayut prosteishie modeli, kak naprimer, sluchai tverdotel'nogo vrasheniya.

<< § 6.4 Chislennoe modelirovanie vspyshek i kollapsa zvezd | Oglavlenie | § 7.2 Vremya relaksacii zvezdnyh sistem >>

Mneniya chitatelei [4]

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce