Astronet > Razmernosti i podobie astrofizicheskih velichin

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Razmernosti i podobie astrofizicheskih velichin << § 5.1 Pul'saciya peremennyh zvezd | Oglavlenie | § 5.3 Turbulentnost' i konvekciya >>

§ 5.2 Vrashenie i magnitnye polya zvezd

Nablyudeniya pokazyvayut, chto zvezdy vrashayutsya i chto na ih poverhnosti imeyutsya magnitnye polya, inogda ochen' sil'nye. Ochevidno, chto vrashayutsya i vnutrennie chasti zvezdy i chto tam tozhe est' magnitnye polya, odnako nikakih svedenii o haraktere vrasheniya central'nyh chastei zvezd i o napryazhennostyah magnitnyh polei vnutri nih u nas net. Poetomu pri issledovanii struktury vrashayushihsya i namagnichennyh zvezd prihoditsya delat' proizvol'nye dopusheniya. Etim problemam posvyasheno mnogo rabot, i v nashu zadachu ne vhodit ih obzor. V chastnosti, interes k vrasheniyu i magnitnym polyam zvezd ochen' vozros posle otkrytiya pul'sarov - vrashayushihsya namagnichennyh neitronnyh zvezd.

My ogranichimsya nekotorymi obsuzhdeniyami metodov teorii analiza razmernostei primenitel'no k etoi probleme, tem bolee opravdannogo, chto trudno sostavit' polnuyu, adekvatnuyu yavleniyam sistemu uravnenii, a eshe trudnee naiti reshenie podobnyh uravnenii.

Razumeetsya, ispol'zovanie tol'ko metoda teorii razmernostei dlya analiza sootnoshenii mezhdu opredelyayushimi parametrami bez resheniya sootvetstvuyushih sistem uravnenii sushestvenno ogranichivaet rassmotrenie problemy. Naprimer, my nichego ne smozhem skazat' o raspredelenii uglovyh skorostei vrasheniya ili magnitnyh polei v nedrah zvezdy. No, s drugoi storony, poluchaemye rezul'taty ne zavisyat ot etih raspredelenii, kotorye do sih por nel'zya ocenit' hotya by skol'ko-nibud' uverenno.

Rassmotrim teper' podrobno nabor opredelyayushih parametrov, kotorye mogut harakterizovat' vrashenie i magnitnye polya zvezd. Vrashenie harakterizuetsya uglovoi skorost'yu Ω;;; s razmernost'yu [Ω;;;] = sek^-1. V real'nyh zvezdah velichina Ω;;; menyaetsya v ochen' shirokih predelah - ot Ω;;; ≈ 200 sek^-1 u pul'sara Krabovidnoi tumannosti do Ω;;; ≈ 2,7 ⋅ 10^-6 sek^-1 u Solnca i, veroyatno, eshe mnogo men'she u zvezd krasnyh gigantov. Poka ne yasno, naskol'ko odnorodno (tverdotel'no) vrashenie zvezdy. Horosho izvestno, chto vrashenie poverhnostnyh sloev Solnca neodnorodno, ekvatorial'nye oblasti vrashayutsya s bol'shei uglovoi skorost'yu, chem polyarnye, a verhnie sloi solnechnoi atmosfery vrashayutsya bystree bolee glubokih sloev. Neodnokratno vyskazyvalos' predpolozhenie, chto yadra zvezd (naprimer, konvektivnye yadra goryachih zvezd) vrashayutsya bystree ostal'noi massy zvezdy. My budem schitat' vrashenie zvezdy tverdotel'nym ili po krainei mere budem rassmatrivat' tol'ko srednyuyu uglovuyu skorost' Ω;;;. Vtoroi sushestvennyi parametr vrashayusheisya zvezdy - ee moment inercii

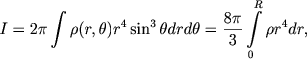
$I = 2\pi\int\rho(r,\theta)r^4\sin^3\theta drd\theta = \frac{8\pi}{3}\int\limits_0^R \rho r^4dr,$ (5.39)

gde, po-prezhnemu, r est' rasstoyanie do centra zvezdy, a θ - ugol mezhdu radiusom-vektorom i os'yu vrasheniya (vtoroe ravenstvo - dlya sluchaya, kogda plotnost' zavisit tol'ko ot r). Velichina momenta inercii sushestvenno zavisit ot raspredeleniya plotnosti vnutri zvezdy, no dlya podobnyh zvezd mozhno napisat'

$I = \zeta_n MR^2,$ (5.40)

gde parametr ζ_n men'she edinicy, a u zvezd s bol'shoi koncentraciei massy k centru (u krasnyh gigantov) mnogo men'she edinicy.

Esli v processe evolyucii zvezdy menyaetsya ee moment inercii (izmenyaetsya kak R, tak i ζ_n, poskol'ku izmenyaetsya koncentraciya veshestva k centru zvezdy), to menyaetsya i uglovaya skorost' v sootvetstvii s zakonom sohraneniya momenta vrasheniya

$\mathfrak{M} = I\Omega = const.$ (5.41)

Pravda, obsuzhdaetsya vopros i o potere momenta vrasheniya v processe evolyucii zvezd. Takaya poterya mozhet byt' vyzvana umen'sheniem massy zvezdy iz-za zvezdnogo vetra, ili zhe moment vrasheniya mozhet otbirat'sya ot zvezdy pri izluchenii eyu magnitogidrodinamicheskih voln (sm. nizhe). Razmernost' momenta vrasheniya, kotoryi takzhe yavlyaetsya opredelyayushim parametrom, est' $\mathfrak {M}$ = g ⋅ sm² ⋅ sek^-1. Eshe odin parametr - lineinuyu skorost' vrasheniya - my ne budem schitat' opredelyayushim. Lineinuyu skorost' vrasheniya legko vyrazit' cherez uglovuyu skorost', a s drugoi storony, v otlichie ot Ω;;; , I i $\mathfrak {M}$ , lineinaya skorost' ne opredelyaet svoistva vrasheniya zvezdy v celom.

Odnako est' eshe odna velichina s razmernost'yu skorosti, kotoraya harakterizuet vrashayushiesya zvezdy. V uravnenii gidrostaticheskogo ravnovesiya naryadu s siloi tyazhesti nado uchest' i centrobezhnuyu silu, kotoraya, v otlichie ot pervoi, ne yavlyaetsya sfericheski-simmetrichnoi, no takzhe lezhit v meridional'nyh ploskostyah. V rezul'tate poverhnosti ravnogo urovnya (odinakovoi velichiny summy gravitacionnogo potenciala i potenciala centrobezhnoi sily) ne sovpadayut so sfericheskimi poverhnostyami odinakovoi velichiny potoka luchistoi energii. Etot effekt privodit k poyavleniyu cirkulyacii veshestva zvezdy v meridional'nyh ploskostyah. Cirkulyacionnaya skorost', oboznachaemaya v dal'neishem cherez v_c, mnogo men'she kak lineinoi skorosti vrasheniya, tak i skorosti konvektivnyh dvizhenii. V konvektivnyh zonah i yadrah podobnoi cirkulyacii net.

Nakonec, poslednii parametr, harakterizuyushii vrashayushiesya zvezdy - koefficient vyazkosti veshestva, stremyashiisya vyrovnyat' neodnorodnost' vrasheniya, sdelat' ego tverdotel'nym. V konvektivnyh zonah i yadrah sushestvenna rol' turbulentnoi vyazkosti i tam vrashenie, po-vidimomu, bystro stanovitsya tverdotel'nym. V oblasti luchistogo perenosa energii rol' vyazkosti, po-vidimomu, mnogo men'she, i tam dol'she mozhet sohranyat'sya neodnorodnost' vrasheniya. V kachestve opredelyayushego parametra vyberem koefficient dinamicheskoi vyazkosti η, po poryadku velichiny ravnyi proizvedeniyu plotnosti na dlinu svobodnogo probega i na skorost' chastic, perenosyashih vrashatel'nyi moment. Razmernost' etoi velichiny [η] = g ⋅ sm^-1 ⋅ sek^-1. Razlichnye koefficienty vyazkosti harakterizuyutsya sootvetstvuyushei dlinoi svobodnogo probega i skorost'yu teh elementov, kotorye perenosyat kolichestvo dvizheniya. V turbulentnoi vyazkosti dlina svobodnogo probega i skorost' opredelyayutsya razmerom i skorost'yu turbulentnyh vihrei.

V ionizovannom gaze vyazkost' opredelyaetsya svobodnym probegom i teplovoi skorost'yu polozhitel'nyh ionov (protonov). Teoriya daet sleduyushuyu formulu dlya koefficienta dinamicheskoi vyazkosti ionizovannoi vodorodnoi plazmy:

$\eta \approx \frac{m_p^3}{e^4\Lambda}\left(\frac{\Re T}{\mu}\right)^{5/2} \approx 0,4 T_6^{5/2} \frac{\mbox{g}}{\mbox{sm} \cdot \mbox{sek}},$ (5.42)

gde Λ - kulonovskii logarifm (Λ ≈ 10-100). V srede s bol'shoi plotnost'yu izlucheniya vyazkost' opredelyaetsya dlinoi svobodnogo probega fotonov. Zdes' imeet mesto dinamicheskii koefficient luchistoi vyazkosti

$\eta = \frac{c}{\varkappa}(1-\beta),$ (5.43)

gde ϰ - obychnyi koefficient neprozrachnosti.

Teper' obratimsya k opredelyayushim parametram magnitnogo polya. Osnovnoi velichinoi yavlyaetsya magnitnaya indukciya V s razmernost'yu

$\eta = \frac{c}{\varkappa}(1-\beta),$ (5.44)

Na poverhnosti zvezd znachenie velichiny V takzhe var'iruetsya v bol'shih predelah - ot velichiny poryadka odnogo gaussa (obshee magnitnoe pole Solnca) do neskol'kih tysyach gauss u magnitnyh zvezd, vozmozhno, 10⁷ gauss u belyh karlikov i, veroyatno, 10¹⁰-10¹² gauss - u pul'sarov.

Struktura magnitnogo polya vnutri zvezd ostaetsya neizvestnoi. Sudya po tomu, chto na poverhnosti Solnca magnitnoe pole imeet slozhnuyu strukturu, mozhno predpolagat', chto i vnutri zvezd imeyutsya slozhnye magnitnye konfiguracii. Poskol'ku seichas pochti nichego nel'zya skazat' ob etoi strukture, chasto predpolagaetsya, chto vnutri zvezd (i, v chastnosti, pul'sarov) magnitnoe pole odnorodno, t. e. vse magnitnye silovye linii parallel'ny nekotoroi magnitnoi osi. Odnorodnoe vnutri zvezdy magnitnoe pole sozdaet vne ego dipol'noe magnitnoe pole s dipol'nym momentom, ravnym

$\Xi = \frac{1}{2}B_0R^3,$ (5.45)

gde B₀ - velichina odnorodnoi magnitnoi indukcii vnutri zvezdy s radiusom R. Kak izvestno, dipol'noe magnitnoe pole yavlyaetsya potencial'nym, t. e. vektor V vne zvezdy mozhet byt' vyrazhen cherez magnitnyi potencial Ψ , v dannom sluchae ravnyi

$\Psi = -\frac{\vec\Xi \vec r}{r^3},$ (5.46)

gde $\vec\Xi$ - vektor, chislennaya velichina kotorogo ravna (5.45), napravlennyi vdol' magnitnoi osi. Dlya polya imeem

$\vec B = grad\Psi.$ (5.47)

Po-vidimomu, magnitnaya os' ne sovpadaet s os'yu vrasheniya zvezdy. U Solnca ugol mezhdu obeimi osyami mal, no vozmozhno, chto u pul'sarov magnitnaya os' dazhe perpendikulyarna k osi vrasheniya.

Chasto vmesto magnitnoi indukcii V upotreblyayut napryazhennost' magnitnogo polya H. Vne zvezdy, gde magnitnaya pronicaemost' pochti tochno ravna edinice, eti velichiny blizki. Odnako vnutri zvezdy, gde raspolozheny istochniki magnitnogo polya, velichiny V i H razlichny i ih raznost' opredelyaetsya namagnichennost'yu veshestva zvezdy. Poskol'ku raspredelenie istochnikov magnitnogo polya vnutri zvezdy neizvestno, my po-prezhnemu budem harakterizovat' magnitnoe pole . vnutri zvezdy tol'ko vektorom $\vec B$ i magnitnym momentom $\vec\Xi$ , razmernost' kotorogo est' g^1/2 ⋅ sm^5/2 ⋅ sek^-1.

Naryadu s dinamicheskoi vyazkost'yu imeetsya i magnitnaya vyazkost', opredelyayushaya zatuhanie magnitnogo polya. Magnitnaya vyazkost' opredelyaetsya elektroprovodnost'yu plazmy, kotoraya v sluchae polnoi ionizacii ravna

$\lambda = \frac{30}{\Lambda}\frac{m_p}{e^2}\left(\frac{\Re T}{\mu}\right)^{3/2}.$ (5.48)

Magnitnaya vyazkost', analogichnaya kineticheskoi vyazkosti v=η/ρ, opredelyaetsya sootnosheniem

$\nu_m = \frac{c^2}{4\pi\lambda} \approx \frac{\Lambda}{80\pi}\frac{e^2c^2}{m_p}\left(\frac{\mu}{\Re T}\right)^{3/2}.$ (5.49)

Razmernost' etih velichin takova:

$[\lambda] = \frac{1}{\mbox{sek}}, \quad [\nu_m] = \frac{\mbox{sm}^2}{\mbox{sek}}.$ (5.50)

Rassmatrivaya magnitnye polya, sleduet uchityvat' velichinu plotnosti energii magnitnogo polya

$\omega = \frac{B^2}{8\pi}$ (5.51)

i velichinu plotnosti magnitnoi sily

$\vec f = \frac{1}{4\pi}[rot\vec B \times \vec B].$ (5.52)

Velichina rot $\vec B$ svyazana s plotnost'yu toka $J$ sootnosheniem

$rot\vec B = \frac{4\pi}{c}\vec J.$ (5.53)

Zdes' sushestvenno to, chto plotnost' toka pri zadannoi koncentracii zaryazhennyh chastic n dolzhna byt' ogranichena, a imenno:

$J < nec = J_{\mbox{krit}}.$ (5.54)

Esli konfiguracii s magnitnymi polyami izmenyayutsya, no tak, chto effektom dissipacii magnitnogo polya mozhno prenebrech', to imeetsya sohranyayushayasya velichina, a imenno potok magnitnoi indukcii $\vec \Phi$ cherez zadannuyu poverhnost'

$\Phi = \int (\vec B d\vec s) \sim BR^2.$ (5.55)

Eto yavlenie prinyato nazyvat' vmorozhennost'yu, ili prikleennost'yu magnitnyh silovyh linii v veshestve. Pri szhatii zvezdy s vmorozhennym magnitnym polem velichina magnitnoi indukcii V rastet kak R², t. e. magnitnyi moment zvezdy Ξ umen'shaetsya proporcional'no radiusu. Takim obrazom, opredelyayushim parametrom skoree yavlyaetsya velichina potoka magnitnoi indukcii Φ , a ne magnitnyi moment Ξ . No uslovie sohraneniya potoka magnitnoi indukcii ne vsegda soblyudaetsya (naprimer, szhatie vdol' magnitnogo polya ego voobshe ne izmenyaet), i poetomu v konkretnyh zadachah prihoditsya otdel'no obsuzhdat' rol' teh ili inyh opredelyayushih parametrov.

Teper' pereidem k poisku svyazi mezhdu razlichnymi opredelyayushimi parametrami vrasheniya i magnitnyh polei zvezd na osnovanii metodov analiza razmernostei. Rassmotrim snachala vrashayushiesya zvezdy, ne uchityvaya effekty magnitnyh polei. Perechislim opredelyayushie parametry dlya etogo sluchaya. Kak obychno, zdes' nado uchityvat' osnovnye parametry zvezd M, L, R i postoyannuyu tyagoteniya G. Vrashenie opisyvaetsya tol'ko dvumya opredelyayushimi parametrami s nezavisimymi razmernostyami: uglovoi skorost'yu vrasheniya Ω;;; i skorost'yu cirkulyacionnyh dvizhenii v_c. Moment inercii i moment vrasheniya srazu vyrazhayutsya cherez drugie parametry i my ispol'zuem eti velichiny tol'ko dlya togo, chtoby vyyasnit' fizicheskii smysl bezrazmernyh kompleksov.

Zapishem matricu razmernosti dlya ukazannyh opredelyayushih parametrov:

$\begin{matrix} \, & [\Omega] & [v_c] & [M] & [L] & [R] & [G] \\ \mbox{g}&0&0&1&1&0&-1 \\ \mbox{sm}&0&1&0&2&1&3 \\ \mbox{sek}&-1&-1&0&-3&0&-2\\ \end{matrix}$

Rang matricy raven trem i, sledovatel'no, imeyutsya tri bezrazmernyh kompleksa s nezavisimymi raz-mernostyami. Poskol'ku my interesuemsya effektami vrasheniya, vyberem, eti bezrazmernye kompleksy tak, chtoby v kazhdyi iz nih vhodila by uglovaya skorost' vrasheniya.

Pri etom uslovii poluchaem tri bezrazmernyh kompleksa. Pervyi iz nih, v kotorom my ne budem uchityvat' svetimost', est'

$\Pi_1 = \frac{\Omega^2 R^2}{GM} = \frac{3}{4\pi}\frac{\Omega^2}{G\bar\rho},$ (5.56)

gde $\bar\rho$ srednyaya plotnost' zvezdy. Vtoroi bezrazmernyi kompleks s uchetom svetimosti

$\Pi_2 = \frac{L R}{G\Omega M^2}.$ (5.57)

I, nakonec, tretii kompleks, vklyuchayushii cirkulyacionnuyu skorost', vyberem sleduyushim obrazom:

$\Pi_3 = \frac{v_c} {\Omega^2}\frac{G^2M^3}{L R^5}.$ (5.58)

Chislennoe znachenie bezrazmernyh kompleksov Π₁, Π₂, Π₃ poka ostaetsya neopredelennym. Obsudim ih fizicheskii smysl.

Legko videt', chto (5.56), po sushestvu, est' sravnenie uskoreniya sily tyazhesti na ekvatore zvezdy GM/R² s sootvetstvuyushim, centrobezhnym uskoreniem Ω;;;²R. Poskol'ku dlya ustoichivosti zvezdy neobhodimo, chtoby centrobezhnaya sila vsegda byla by sushestvenno men'she sily tyazhesti, to otsyuda sleduet, chto u ustoichivyh vrashayushihsya zvezd Π₁ ≪ 1.

Vtoroi bezrazmernyi kompleks est' otnoshenie energii, izluchennoi zvezdoi za vremya odnogo perioda obrasheniya, delennogo na 2π, k velichine, harakterizuyushei polnuyu gravitacionnuyu energiyu zvezdy (t. e. GM²/R). Ochevidno, chto i etot bezrazmernyi kompleks v ustoichivyh stacionarnyh zvezdah mnogo men'she edinicy.

Uslovie malosti oboih bezrazmernyh kompleksov, Π₁ i Π₂, imeet vpolne opredelennyi fizicheskii smysl - sostoyanie vrasheniya ne zavisit ot osnovnyh parametrov zvezdy i yavlyaetsya nezavisimym sledstviem nachal'nyh uslovii obrazovaniya zvezd. Zvezdy s odnimi i temi zhe znacheniyami M, L i R mogut vrashat'sya s razlichnymi uglovymi skorostyami.

Ob'yasnenie tret'ego bezrazmernogo kompleksa Π₃ neskol'ko slozhnee. Srazu vidno, chto etot kompleks takzhe nezavisim - ego nel'zya svesti k kompleksam Π₁ i Π₂, poskol'ku ni odin iz nih ne vklyuchaet cirkulyacionnuyu skorost'. S drugoi storony, tak zhe srazu vidno, chto vybor etogo kompleksa ne odnoznachen, poetomu privedem obosnovanie dlya takogo vybora. Perepishem (5.58) v vide

$\frac{GM}{R^2}v_c = \frac{\Omega^2 R^3}{GM}\frac{L}{M}\Pi_3$ (5.59)

i uchtem, chto, po opredeleniyu, v_c est' cirkulyacionnaya skorost', poyavlyayushayasya v zvezdah s luchistym perenosom energii blagodarya nesovpadeniyu ekvipotencial'nyh urovnei (ravnoi summy gravitacionnogo i centrobezhnogo potencialov) i poverhnostei ravnogo potoka luchistoi energii.

V (5.59) pervyi mnozhitel' sprava est' otnoshenie centrobezhnoi sily k sile gravitacii, vyzyvayushei eto nesovpadenie poverhnostei. Velichina GM/R² est' uskorenie sily tyazhesti i poetomu proizvedenie v_cGM/R² est' rabota, sovershaemaya cirkulyaciei nad edinicei massy veshestva za edinicu vremeni. Nakonec, L/M ≈ L_r/M_r est' divergenciya potoka luchistoi energii, takzhe otnesennaya k edinice massy, t. e. kak by "stok" luchistoi energii v dannom sloe v drugie formy energii - v dannom sluchae v rabotu cirkulyacii.

Sopostavlyaya eti zatraty raboty, mozhno schitat', chto bezrazmernyi kompleks Π₃ dolzhen byt' poryadka edinicy. Bolee togo, podobnoe sootnoshenie spravedlivo ne tol'ko dlya srednego po vsei zvezde znacheniya cirkulyacionnoi skorosti, no i dlya ee znachenii v kazhdoi tochke vnutri zvezdy. Po poryadku velichiny imeem:

$v_c(r) = \frac{\Omega^2 r^2L(r)}{G^2\rho(r)[M(r)]^2}.$ (5.60)

Podrobnoe opisanie effekta meridional'noi cirkulyacii dano v knige Shvarcshil'da [10] i v stat'e Mestelya v sbornike [11]. Pervonachal'no cirkulyaciya iz-za vrasheniya rassmatrivalas' kak effektivnyi mehanizm peremeshivaniya veshestva - process, vazhnyi dlya opredeleniya evolyucii zvezd. Odnako, kak sleduet iz (5.59) i (5.60),chislennoe znachenie skorosti cirkulyacii ochen' malo (u Solnca - okolo 10^-9 sm ⋅ sek^-1) i tol'ko v poverhnostnyh sloyah bystrovrashayushihsya zvezd ona mozhet byt' zametnoi, tak kak v_c ∼ Ω;;;²R⁵. Po-vidimomu, vse zhe rol' meridional'noi cirkulyacii v peremeshivanii zvezdnogo veshestva i, sledovatel'no, v zvezdnoi evolyucii nevelika.

Iz soobrazhenii analiza razmernostei netrudno poluchit' i ocenku harakternogo vremeni vyravnivaniya neodnorodnosti vrasheniya. Zdes' est' sleduyushie opredelyayushie parametry: gradient uglovoi skorosti, kotoryi my oboznachim cherez dΩ;;;/dr, s razmernost'yu [dΩ;;;/dr] = sm^-1 ⋅ sek^-1, dinamicheskaya vyazkost' η, opredelennaya formulami (5.42) ili (5.43), plotnost' veshestva ρ i, nakonec, harakternoe vremya dissipacii t_diss, v techenie kotorogo neodnorodnoe vrashenie stanet priblizitel'no odnorodnym. My vypisyvaem parametry, opisyvayushie usloviya v dannom meste, a ne obshie parametry zvezdy, poskol'ku effekt vyravnivaniya uglovyh skorostei, - perehod k tverdotel'nomu vrasheniyu, - est' differencial'nyi, a ne integral'nyi effekt, harakterizuyushii povedenie otdel'nyh chastei zvezdy.

Sostavlyaem matricu razmernosti:

$\begin{matrix} \, & [\frac{d\Omega}{dr}] & [\eta] & [t] & [\rho] \\ \mbox{g}&0&1&0&1 \\ \mbox{sm}&-1&-1&0&-3 \\ \mbox{sek}&-1&-1&1&0 \\ \end{matrix}$

Edinstvennyi bezrazmernyi kompleks:

$\Pi = \frac{d\Omega}{dr}\left(\frac{\eta}{\rho}\right)^{1/2}t_{\mbox{diss}}^{3/2}.$ (5.61)

V sluchae zametnogo effekta vyravnivaniya uglovyh skorostei iz-za deistviya vyazkosti etot bezrazmernyi kompleks dolzhen byt' poryadka edinicy. Otsyuda harakternoe vremya ustanovleniya tverdotel'nosti vrasheniya:

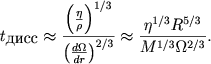
$t_{\mbox{diss}} \approx \frac{\left(\frac{\eta}{\rho}\right)^{1/3}}{\left(\frac{d\Omega}{dr}\right)^{2/3}} \approx \frac{\eta^{1/3}R^{5/3}}{M^{1/3}\Omega^{2/3}}.$ (5.62)

Eta velichina mala po sravneniyu s harakternym vremenem polnoi evolyucii zvezdy (u Solnca ~ 5 ⋅ 10⁶ let), no na ee otdel'nyh etapah netverdotel'nost' vrasheniya vpolne vozmozhna. Naprimer, perehod k stadii krasnogo giganta mozhet byt' svyazan s obrazovaniem bystro-vrashayushegosya yadra v centre zvezdy i gorazdo bolee medlenno vrashayusheisya obolochki.

Teper' obratimsya k analizu metodami teorii razmernostei uslovii namagnichennosti zvezd. Prezhde vsego naidem opredelyayushie parametry. Krome ochevidnyh velichin G, M, R, L sleduet uchest' vrashenie - parametr Ω;;; i magnitnuyu indukciyu V. Magnitnye polya, po-vidimomu, ne vyzyvayut kakih-libo sistematicheskih dvizhenii veshestva vnutri zvezd i poetomu zdes' net parametra, analogichnogo cirkulyacionnoi skorosti v_c. No, s drugoi storony, vo vseh elektromagnitnyh yavleniyah vsegda opredelyayushim parametrom dolzhna byt' skorost' sveta. Itak, ogranichimsya sleduyushim naborom opredelyayushih parametrov: V, Ω;;; , M, R, L, G, s. Otsyuda sleduet matrica razmernosti:

$\begin{matrix} \, & [B] & [\Omega] & [M] & [R] & [L] & [G] & [c] \\ \mbox{g}&1/2&0&1&0&1&-1&0 \\ \mbox{sm}&-1/2&0&0&1&2&3&1 \\ \mbox{sek}&-1&-1&0&0&-3&-2&-1 \\ \end{matrix}$

Ee rang raven trem i, sledovatel'no, est' chetyre nezavisimyh bezrazmernyh kompleksa. Po sravneniyu s bezrazmernymi kompleksami (5.56) - (5.68) zdes', po sushestvu, est' tol'ko odin novyi bezrazmernyi kompleks, svyazannyi s poyavleniem eshe odnogo opredelyayushego parametra. Bezrazmernye kompleksy (5.56) i (5.57) voobshe mozhno ostavit' bez izmeneniya:

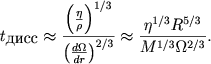
$t_{\mbox{diss}} \approx \frac{\left(\frac{\eta}{\rho}\right)^{1/3}}{\left(\frac{d\Omega}{dr}\right)^{2/3}} \approx \frac{\eta^{1/3}R^{5/3}}{M^{1/3}\Omega^{2/3}}.$ (5.63)

Kak my uzhe videli, eti kompleksy, po sushestvu, nichego ne dayut, t. e. uglovaya skorost' vrasheniya ne zavisit neposredstvenno ot osnovnyh parametrov, harakterizuyushih zvezdu. Takoi zhe harakter imeet i bezrazmernyi kompleks

$\Pi_3 = \frac{B^2 R^4}{GM^2} = 6\frac{B^2}{8\pi}\frac{4\pi R^3}{3}\frac{R}{GM^2}.$ (5.64)

Zdes' V²/8π - harakternaya velichina magnitnogo davleniya, a GM²/R⁴ - harakternaya velichina davleniya, uderzhivayushego zvezdu v stacionarnom sostoyanii. Takim obrazom, $\frac{B^2}{8\pi}\frac{4\pi}{3}R^3$ est' polnaya magnitnaya energiya zvezdy, a GM³/R - ee gravitacionnaya energiya. Otsyuda sleduet, chto Π₃ ne malo po sravneniyu s edinicei tol'ko u takih zvezd, u kotoryh magnitnoe davlenie igraet sushestvennuyu rol' v balanse vseh davlenii. Est' li takie ob'ekty v kosmicheskih usloviyah - poka skazat' trudno. U Solnca kompleks Π₃ nichtozhno mal, u magnitnyh gazovyh zvezd i pul'sarov velichina Π₃ takzhe ochen' mala, poryadka 10^-13, tak chto, veroyatno, bezrazmernye kompleksy Π₁, Π₂ i Π₃ dlya vseh real'nyh zvezd est' malye velichiny i, sledovatel'no, poetomu vryad li mogut sluzhit' kriteriyami podobiya.

No, v otlichie ot bezrazmernyh kompleksov (5.63), kotorye mogut menyat'sya ne tol'ko ot zvezdy k zvezde, no i u odnoi i toi zhe zvezdy v processe ee evolyucii, bezrazmernyi kompleks (5.64) ostaetsya postoyannym dlya dannoi zvezdy, esli vypolneno uslovie sohraneniya magnitnogo potoka (5.55). V samom dele, s uchetom, (5.55) sootnoshenie (5.64) mozhet byt' zapisano v vide

$\Pi_3 = \Phi^2G^{-1}M^{-2}.$ (5.65)

Vse parametry, vhodyashie v bezrazmernyi kompleks (5.65), ne menyayutsya v processe evolyucii, esli sohranyayutsya usloviya vmorozhennosti i massa zvezdy. Analogichnoe uslovie dlya vrasheniya zvezdy imelo by mesto, esli by mozhno bylo postroit' bezrazmernyi kompleks iz treh sohranyayushihsya v processe evolyucii velichin $\mathfrak{M}$ (5.41), M i G. Odnako eto nevozmozhno.

Chetvertyi bezrazmernyi kompleks vklyuchaet skorost' sveta:

$\Pi_4 = \frac{cBR}{G^{1/2}M\Omega}.$ (5.66)

Chtoby prinyat' smysl etogo bezrazmernogo kompleksa, perepishem ego v sleduyushem vide:

$\Pi_4 = 2\zeta_n\frac{c\Xi}{G^{1/2}\mathfrak{M}}.$ (5.67)

gde my vospol'zovalis' formulami (5.40), (5.41) i (5.45). Napomnim, chto ζ_n est' bezrazmernyi mnozhitel', opredelyayushii moment inercii tela.

Kak uzhe otmechalos', v real'nyh zvezdah bezrazmernye kompleksy Π₁, Π₂ (5.63) i Π₃ (5.64) na mnogo poryadkov men'she edinicy i sushestvenno razlichny u raznyh zvezd. Po-inomu vedet sebya kompleks Π₄ (5.66). Esli podstavit' syuda chislennye znacheniya parametrov, sootvetstvuyushih Solncu ili pul'saram, to v oboih sluchayah poluchayutsya blizkie po poryadku velichiny znacheniya, sravnimye s 10^-3. Vozmozhno takzhe, chto bezrazmernaya velichina $\frac{c\Xi}{G^{1/2}\mathfrak{M}}$ i blizhe k edinice, tak kak ζ_n obychno malo.

Etot rezul'tat uzhe bolee interesen. Esli prinyat', chto ne slishkom malaya velichina otnosheniya $\frac{c\Xi}{G^{1/2}\mathfrak{M}}$ svidetel'stvuet ob odinakovosti etogo otnosheniya dlya raznyh ob'ektov, to otsyuda sleduet utverzhdenie o tom, chto magnitnyi moment zvezdy proporcionalen ee momentu vrasheniya:

$\Xi \approx A\frac{\sqrt G}{c}\mathfrak{M},$ (5.68)

gde A - bezrazmernaya postoyannaya poryadka edinicy. Imenno takoe utverzhdenie bylo vyskazano eshe v v 1947 g. Blekketom,. Eta gipoteza v to vremya mnogo obsuzhdalas', no v konechnom schete byla ostavlena, poskol'ku ne vidno fizicheskih yavlenii, kotorye privodili by k proporcional'nosti mezhdu momentom vrasheniya i magnitnym momentom u zvezd (i planet, po Blekketu) raznyh tipov. Ne vidno fizicheskogo obosnovaniya etoi gipotezy i seichas, no sootnosheniya analiza razmernostei vse zhe dopuskayut takuyu zavisimost'. Vazhno, chto koefficient proporcional'nosti mezhdu magnitnym momentom i momentom vrasheniya vyrazhaetsya tol'ko cherez universal'nye postoyannye G i s.

V atomnoi fizike tozhe imeetsya universal'naya svyaz' mezhdu magnitnym momentom i momentom vrasheniya (ili spinovym momentom) elementarnyh chastic i atomov. Zdes' koefficient proporcional'nosti vyrazhaetsya cherez zaryad i massu elementarnyh chastic. Dlya tyazhelyh chastic

$\Xi \approx A\frac{e}{m_p c}\mathfrak{M},$ (5.69)

gde A - po-prezhnemu poryadka edinicy *).

Otnoshenie razmernyh koefficientov proporcional'nosti v (5.68) i (5.69) ravno

$\frac{m_p G^{1/2}}{e} = \left(\frac{\delta}{\alpha}\right)^{1/2},$ (5.70)

gde, napominaem, α i δ - postoyannye elektromagnitnogo i gravitacionnogo vzaimodeistviya elementarnyh chastic.

Vse zhe, po-vidimomu, sootnoshenie Blekketa (5.68) zasluzhivaet bolee vnimatel'nogo izucheniya. Podschitaem velichinu A v (5.68), ispol'zuya nablyudatel'nye dannye po ryadu astronomicheskih ob'ektov, ne ogranichivayas' tol'ko zvezdami.

V tabl. 8 dany znacheniya ishodnyh parametrov, po kotorym vychislena velichina A iz formuly (5.68).

Tablica 8

Ob'ekt	B, gs	Ξ , $\frac{\mbox{g}^{1/2}\mbox{sm}^{5/2}}{\mbox{sek}}$	$\mathfrak{M}, \, \frac{\mbox{g}\mbox{sm}^{2}}{\mbox{sek}}$	A
Zemlya	0,5	8 ⋅ 10²⁵	5,9 ⋅ 10⁴⁰	0,16
Solnce	2	2 ⋅ 10³²	(1-6) ⋅ 10⁴⁸	0,01
Pul'sar	10¹²	5 ⋅ 10²⁹	2 ⋅ 10⁴⁶	0,003
Galaktika	10^-6	5 ⋅ 10⁵⁹	2 ⋅ 10⁷³	1

Itak, u raznyh ob'ektov parametr A zametno razlichaetsya, no ved' i eti ob'ekty imeyut sushestvenno razlichnuyu prirodu. Poskol'ku parametr A vo mnogih sluchayah mal po sravneniyu s edinicei, to mal i bezrazmernyi kompleks Π₄ (5.67) (tak kak Π₄ = 2ζ_nA, a ζ_n < 1). No tem ne menee on vse zhe na poryadki bol'she chislennyh znachenii bezrazmernyh kompleksov (5.63) i (5.65). Poetomu (5.66) poka edinstvennaya ne ochen' malaya bezrazmernaya kombinaciya, kotoruyu mozhno sosta< vit' iz osnovnyh parametrov zvezdy, ee magnitnogo polya i uglovoi skorosti vrasheniya.

Obsheizvestno, chto vremya dzhoulevoi dissipacii magnitnogo polya v kosmicheskih ob'ektah ochen' veliko, chasto na poryadki velichin bol'she vremeni evolyucii etih ob'ektov. Sootvetstvuyushie ocenki mozhno takzhe poluchit', ispol'zuya soobrazheniya razmernosti, esli uchest' sleduyushii nabor opredelyayushih parametrov: koefficient magnitnoi vyazkosti ν_m (5.49), razmer oblasti R, gde imeet mesto zatuhanie, i harakternoe vremya zatuhaniya t_diss. Iz etih treh velichin mozhno obrazovat' odin bezrazmernyi kompleks, iz kotorogo sleduet, chto harakternoe vremya zatuhaniya magnitnogo polya

$t_{\mbox{diss}} \approx \frac{R^2}{\nu_m}.$ (5.71)

My ne vklyuchili v chislo opredelyayushih parametrov ni velichinu V, ni ee gradient tipa dB/dr, kak eto bylo sdelano v analogichnoi zadache po opredeleniyu dissipacionnogo processa vyravnivaniya uglovyh skorostei v formule (5.62). Delo v tom, chto v dannom sluchae ocenivaetsya ischeznovenie vsego polya, kotoroe proishodit vo vsem ob'eme i ne prekrashaetsya do teh por, poka vse pole ne dissipiruet. V sootnosheniyah (5.61) - (5.62) ocenivalsya lish' perehod k tverdotel'nomu vrasheniyu, kotoroe, estestvenno, opredelyaetsya gradientom uglovyh skbrostei. Nezavisimost' (5.71) ot V opredelyaetsya lineinost'yu uravnenii magnitnoi indukcii, opisyvayushih i dissipaciyu magnitnyi polei.

Velichina ν_m, rasschitannaya po molekulyarno-kineticheskoi teorii, sravnitel'no mala, i poetomu bol'shie razmery zvezd privodyat k bol'shomu vremeni zatuhaniya. Odnako v plazme imeyut mesto raznoobraznye kollektivnye processy, kotorye mogut na mnogo poryadkov uvelichit' ν_m (t. e. umen'shit' provodimost' plazmy). Poetomu s uchetom kollektivnyh processov vremya dissipacii magnitnogo polya mozhet byt' i ne stol' bol'shim. Analiz vseh etih voprosov vyhodit za ramki nastoyashei knigi.

V zaklyuchenie nastoyashego paragrafa rassmotrim vopros o potere momenta vrasheniya i magnitnogo polya zvezdy blagodarya izlucheniyu voln. Delo zdes' v sleduyushem. Kak horosho izvestno, vrashayushiisya zaryad izluchaet elektromagnitnye volny s chastotoi, ravnoi uglovoi skorosti vrasheniya ili ee garmonikam. Ochevidno, chto vrashayushiisya magnitnyi dipol' tozhe dolzhen izluchat' elektromagnitnye volny s chastotoi, ravnoi uglovoi skorosti vrasheniya. Opredelim moshnost' izlucheniya takih voln. Snachala budem schitat', chto vrashayushiisya magnitnyi dipol' s momentom Ξ nahoditsya v vakuume, tak chto nichto ne meshaet rasprostraneniyu izluchaemyh im voln. Ispol'zuem soobrazheniya analiza razmernostei. Ochevidno, chto opredelyayushih parametrov vsego chetyre: moshnost' izlucheniya, kotoruyu my oboznachim cherez L_m, magnitnyi moment uglovaya chastota vrasheniya Ω;;; i skorost' rasprostraneniya voln s. Matrica razmernosti imeet sleduyushii vid:

$\begin{matrix} \, & [L_m] & [\Xi] & [\Omega] & [c] \\ \mbox{g}&1&1/2&0&0 \\ \mbox{sm}&2&5/2&0&1 \\ \mbox{sek}&-3&-1&-1&1 \\ \end{matrix}$

Imeetsya tol'ko odin bezrazmernyi kompleks

$\Pi = L_mc^3\Xi^{-2}\Omega^{-4}.$ (5.72)

Velichina Π dolzhna zaviset' ot geometrii sistemy. Tochnyi raschet pokazyvaet, chto dipol', vrashayushiisya vokrug osi vrasheniya pod uglom, θ k etoi osi, izluchaet elektromagnitnye volny s moshnost'yu

$L_m = \frac{2}{3}\frac{\Xi^2\Omega^4}{c^3}\sin^2\theta.$ (5.73)

Esli schitat', chto polnaya svetimost' pul'sara poryadka L_m, to, po krainei mere dlya pul'sara v Krabovidnoi tumannosti, formula (5.73) daet ocenku Ξ ≈ 6 ⋅ 10²⁹ g^1/2sm^5/2sek^-1.

Na samom dele polozhenie slozhnee. Delo v tom, chto formula (5.73) spravedliva lish' dlya sluchaya, kogda skorost' rasprostraneniya elektromagnitnyh voln s chastotoi Ω;;; blizka k s i kogda voobshe vozmozhno rasprostranenie takih voln. Svoistva okruzhayushei pul'sar plazmy mogut sushestvenno izmenit' usloviya izlucheniya nizkochastotnyh voln. Naprimer, vrashayushiisya v plazmennoi srede magnitnyi dipol' izluchaet takzhe al'venovskie volny, skorost' rasprostraneniya kotoryh zavisit kak ot plotnosti sredy, tak i ot napravleniya rasprostraneniya. Polnaya moshnost' izlucheniya mozhet zametno otlichat'sya ot (5.73), v chastnosti, velichina L_m mozhet byt' proporcional'na i drugoi stepeni chastoty. Zdes' trebuetsya bolee podrobnyi analiz, i soobrazheniya metoda razmernostei okazyvayutsya nedostatochnymi.

Energiya, izluchaemaya etimi volnami, zabiraetsya iz kineticheskoi energii vrasheniya, ravnoi ½IΩ;;;². Odno vremenno eti zhe volny unosyat i moment vrasheniya. Iz (5.73) srazu sleduet, chto izluchenie elektromagnitnyh voln vrashayushimsya magnitnym dipolem, privodit k tormozheniyu vrasheniya, t. e. umen'sheniyu ego uglovoi skorosti v sootvetstvii s formuloi

$\frac{d\Omega}{dt} = -\frac{2}{3}\frac{\Xi^2\Omega^3}{Ic^3}\sin^2\theta.$ (5.74)

Etu zavisimost' mozhno proverit' na pul'sarah (sm. [12]), gde, blagodarya maloi velichine perioda, mozhno nablyudat' ego izmenenie. Pravda, my ne znaem tochno ni magnitnogo momenta pul'sara Ξ , ni ego momenta inercii I. Poetomu predpolozhim, chto izmenenie chastoty proporcional'no ee nekotoroi stepeni, t. e.

$\frac{d\Omega}{dt} \sim \Omega^n$ (5.75)

Differenciruya eto sootnoshenie, nahodim uslovie

$n = \frac{\Omega}{\frac{d\Omega}{dt}}\frac{d^2\Omega}{dt^2}.$ (5.76)

Kazhdaya iz velichin v pravoi chasti v principe mozhet byt' opredelena iz nablyudenii. V 1975 g. dannyh nablyudenii bylo eshe nedostatochno. Uverenno nablyudalas' vtoraya proizvodnaya lish' u pul'sara v Krabovidnoi tumannosti. V etom sluchae okazalos' primerno n ≈ 3,5. Po drugim pul'saram uverennyh dannyh net, no statisticheskii analiz privodit k srednemu znacheniyu n ≈ 2,4 [12]. Mozhno nadeyat'sya, chto v budushem bol'shie ryady nablyudenii pul'sarov pozvolyat tochnee opredelit' pokazatel' stepeni v (5.75).

Est' i drugie mehanizmy izmeneniya uglovoi skorosti vrasheniya, naprimer, poterya massy. No my rassmotrim bolee ekzoticheskii sluchai - effekt izlucheniya gravitacionnyh voln vrashayusheisya zvezdoi. Effektivnost' etogo mehanizma sushestvenno zavisit ot nesferichnosti zvezdy, tochnee, ot velichiny ee kvadrupol'nogo momenta, kotoryi mozhno opredelit' velichinoi

$Q = \chi_nMR^2,$ (5.77)

gde chislennyi koefficient zavisyashii ot raspredeleniya massy v zvezde i ot ee nesferichnosti, mozhet byt' ochen' mal. Naidem moshnost' izlucheniya gravitacionnyh voln na osnove soobrazhenii razmernosti. Opredelyayushimi parametrami budut Q, uglovaya skorost' Q, skorost' rasprostraneniya gravitacionnyh voln, ravnaya skorosti sveta c, i postoyannaya tyagoteniya N'yutona, naryadu s samoi velichinoi moshnosti L_g, kotoruyu sleduet opredelit'. Matrica razmernosti:

$\begin{matrix} \, & [L_g] & [Q] & [\Omega] & [c] & [G] \\ \mbox{g}&1&1&0&0&-1 \\ \mbox{sm}&2&2&0&1&3 \\ \mbox{sek}&-3&0&-1&-1&-2 \\ \end{matrix}$

Edinstvennyi bezrazmernyi kompleks:

$\Pi = L_g c^5 G^{-1}Q^{-2}\Omega^{-6}$ (5.78)

Tochnaya formula dlya moshnosti izlucheniya gravitacionnyh voln imeet vid [13]

$L_g = \frac{GQ^2}{45c^5}\Omega^6.$ (5.79)

Otsyuda izmenenie uglovoi skorosti pri izluchenii gravitacionnyh voln

$\frac{d\Omega}{dt} = -\frac{1}{45}\frac{GQ^2}{Ic^5}\Omega^5,$ (5.80)

t. e. eshe sil'nee rashoditsya s nablyudennym u pul'sarov znacheniem pokazatelya n v (5.75). Ne budem obsuzhdat' eti rashozhdeniya, no otmetim tol'ko odno lyubopytnoe sopostavlenie formul (5.79) i (5.74). Imeem dlya otnosheniya obeih moshnostei izlucheniya:

$\frac{L_g}{L_m} = \frac{1}{30\sin^2\theta}\frac{GQ^2\Omega^2}{\Xi^2c^5} = \frac{\chi^2_n}{15\zeta^2_n\sin^2\theta}\frac{G\mathfrak{M}^2}{c^2\Xi^2},$ (5.81)

gde ispol'zovana formula (5.40). Poslednii mnozhitel' v etoi formule est' postoyannaya velichina, esli pravil'no sootnoshenie Blekketa. Bezrazmernyi mnozhitel' dlya dannoi modeli tozhe postoyanen, hotya obychno on ochen' mal. Takim obrazom, esli spravedliva gipoteza Blekketa o proporcional'nosti mezhdu momentom vrasheniya i magnitnym momentom, to otsyuda sleduet proporcional'nost' mezhdu moshnostyami izlucheniya gravitacionnyh i elektromagnitnyh voln vrashayushimsya magnitnym dipolem.

*) N. R. Sibgatullin obratil nashe vnimanie eshe na odin primer, illyustriruyushii gipotezu Blekketa. Formula (5.69) spravedliva dlya sootnosheniya mezhdu mehanicheskim i magnitnym momentami vrashayushihsya naryazhennyh "chernyh dyr" (reshenie Kerra - N'yumena). V etom sluchae pod e sleduet ponimat' zaryad "chernoi dyry", vmesto m_p podstavit' ee massu, a A = 1.

<< § 5.1 Pul'saciya peremennyh zvezd | Oglavlenie | § 5.3 Turbulentnost' i konvekciya >>

Mneniya chitatelei [4]

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce