
Geometriya zvezdnogo neba
V.Yu. Protasov
Moskovskii Gosudarstvennyi Universitet, Mehaniko-matematicheskii fakul'tet, Vorob'evy Gory, Moskva, 119992, e-mail: v-protassov@yandex.ru
Nebo nad golovoi - samyi drevnii uchebnik geometrii. Pervye
ponyatiya, takie kak tochka i krug - ottuda. Skoree dazhe ne uchebnik,
a zadachnik. V kotorom otsutstvuet stranichka s otvetami. Dva kruga
odinakovogo razmera - Solnce i Luna, dvizhutsya po nebu, kazhdyi so
svoei skorost'yu. Ostal'nye ob'ekty - svetyashiesya tochki, dvizhutsya
vse vmeste, slovno oni prikrepleny k sfere, vrashayusheisya so
skorost'yu 1 oborot v 24 chasa. Pravda, sredi nih est' isklyucheniya -
5 tochek dvizhutsya kak im vzdumaetsya. Dlya nih podobrali osoboe slovo
- "planeta", po-grecheski - "brodyaga". Skol'ko chelovechestvo
sushestvuet, ono pytaetsya razgadat' zakony etogo vechnogo dvizheniya.
Pervyi proryv proizoshel v 3 veke do n.e., kogda grecheskie uchenye,
vzyav na vooruzhenie moloduyu nauku - geometriyu, smogli poluchit'
pervye rezul'taty ob ustroistve Vselennoi. Ob etom i poidet rech'.
Chtoby imet' nekotoroe predstavlenie o slozhnosti zadachi, rassmotrim
takoi primer. Predstavim sebe svetyashiisya shar diametrom 10 sm.,
nepodvizhno visyashii v prostranstve. Nazovem ego ![]() . Vokrug nego na
rasstoyanii chut' bol'she 10 metrov obrashatsya malen'kii sharik
. Vokrug nego na
rasstoyanii chut' bol'she 10 metrov obrashatsya malen'kii sharik ![]() diametrom 1 millimetr, a vokrug
diametrom 1 millimetr, a vokrug ![]() na rasstoyanii
na rasstoyanii ![]() sm.
obrashaetsya sovsem krohotnyi sharik
sm.
obrashaetsya sovsem krohotnyi sharik ![]() , ego diametr - chetvert'
millimetra. Na poverhnosti srednego sharika
, ego diametr - chetvert'
millimetra. Na poverhnosti srednego sharika ![]() zhivut
mikroskopichekie sushestva. Oni obladayut nekim razumom, no pokidat'
predely svoego sharika ne mogut. Vse chto oni mogut - smotret' na
dva drugih shara -
zhivut
mikroskopichekie sushestva. Oni obladayut nekim razumom, no pokidat'
predely svoego sharika ne mogut. Vse chto oni mogut - smotret' na
dva drugih shara - ![]() i
i ![]() . Sprashivaetsya, mogut li oni uznat'
diametry etih sharov, i izmerit' rasstoyaniya do nih ? Skol'ko ni
dumai, delo, kazalos' by, beznadezhnoe. My narisovali sil'no
umen'shennuyu model' Solnechnoi sistemy (
. Sprashivaetsya, mogut li oni uznat'
diametry etih sharov, i izmerit' rasstoyaniya do nih ? Skol'ko ni
dumai, delo, kazalos' by, beznadezhnoe. My narisovali sil'no
umen'shennuyu model' Solnechnoi sistemy (![]() - Solnce,
- Solnce, ![]() - Zemlya,
- Zemlya,
![]() - Luna). Vot takaya zadacha stoyala pered drevnimi astronomami.
I oni ee reshili ! Bolee 22 vekov nazad, ne pol'zuyas' nichem, krome
s samoi elementarnoi geometrii, na urovne 8 klassa (svoistva
pryamoi i okruzhnosti, podobnye treugol'niki i teorema Pifagora). I,
konechno, nablyudaya za Lunoi i za Solncem. Nad resheniem trudilis'
neskol'ko uchenyh. My vydelim dvuh. Eto matematik Eratosfen,
izmerivshii radius zemnogo shara, i astronom Aristarh, vychislivshii
razmery Luny, Solnca i rasstoyaniya do nih. Kak oni eto sdelali ?
- Luna). Vot takaya zadacha stoyala pered drevnimi astronomami.
I oni ee reshili ! Bolee 22 vekov nazad, ne pol'zuyas' nichem, krome
s samoi elementarnoi geometrii, na urovne 8 klassa (svoistva
pryamoi i okruzhnosti, podobnye treugol'niki i teorema Pifagora). I,
konechno, nablyudaya za Lunoi i za Solncem. Nad resheniem trudilis'
neskol'ko uchenyh. My vydelim dvuh. Eto matematik Eratosfen,
izmerivshii radius zemnogo shara, i astronom Aristarh, vychislivshii
razmery Luny, Solnca i rasstoyaniya do nih. Kak oni eto sdelali ?
 E.N.Koneva, M.V.Perepuhov. Cherez terniii k zvezdam |
 Ris. 1. |
Dlya sovremennikov Eratosfen byl znamenit kak krupneishii
uchenyi-enciklopedist, zanimavshiisya ne tol'ko matematikoi, no i
geografiei, kartografiei i astronomiei. On dolgoe vremya vozglavlyal
Aleksandriiskuyu biblioteku - centr mirovoi nauki togo vremeni.
Rabotaya nad sostavleniem pervogo atlasa Zemli (rech', konechno, shla
ob izvestnoi k tomu vremeni ee chasti), on zadumal provesti tochnoe
izmerenie zemnogo shara. Ideya byla takova. V Aleksandrii vse
znali, chto na yuge, v gorode Siena (sovremennyi Asuan) odin den' v
godu, v polden', Solnce dostigaet zenita. Ischezaet ten' ot
vertikal'nogo shesta, na neskol'ko minut osveshaetsya dno kolodca.
Proishodit eto v den' letnego solncestoyaniya, 22 iyunya - den'
naivysshego polozheniya Solnca na nebe. Eratosfen napravlyaet svoih
pomoshnikov2
v Sienu, i te ustanavlivayut, chto rovno v polden' (po solnechnym chasam)
Solnce nahoditsya tochno v zenite. Odnovremenno (kak napisano v
pervoistochnike: "v tot zhe chas"), t.e., v polden' po solnechnym
chasam, Eratosfen izmeryaet dlinu teni ot vertikal'nogo shesta v
Aleksandrii. Poluchilsya treugol'nik ![]() (
(![]() - shest,
- shest, ![]() -
ten', ris.2).
-
ten', ris.2).
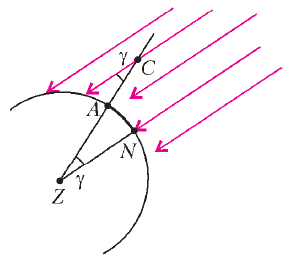 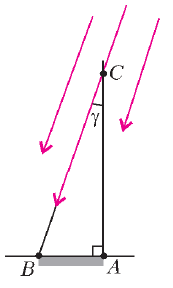 Ris. 2. |
Itak, solnechnyi luch v Siene perpendikulyaren
poverhnosti Zemli, a znachit prohodit cherez ee centr - tochku ![]() .
Parallel'nyi emu luch v Aleksandrii sostavlyaet ugol
.
Parallel'nyi emu luch v Aleksandrii sostavlyaet ugol
![]() s vertikal'yu. Pol'zuyas' ravenstvom nakrestlezhashih
uglov pri parallel'nyh, zaklyuchaem, chto
s vertikal'yu. Pol'zuyas' ravenstvom nakrestlezhashih
uglov pri parallel'nyh, zaklyuchaem, chto
![]() . Esli oboznachit' cherez cherez
. Esli oboznachit' cherez cherez ![]() dlinu okruzhnosti, a
cherez
dlinu okruzhnosti, a
cherez ![]() dlinu ee dugi
dlinu ee dugi ![]() , to poluchaem proporciyu
, to poluchaem proporciyu
![]() . Ugol
. Ugol ![]() v
treugol'nike
v
treugol'nike ![]() Eratosfen izmeril, poluchilos'
Eratosfen izmeril, poluchilos' ![]() .
Velichina
.
Velichina ![]() - ne chto inoe, kak dlina puti ot Aleksandrii do
Sieny, primerno
- ne chto inoe, kak dlina puti ot Aleksandrii do
Sieny, primerno ![]() km. Ee Eratosfen akkuratno vychislyaet, ishodya
iz srednego vremeni dvizheniya verblyuzh'ih karavanov, regulyarno
hodivshih mezhdu dvumya gorodami, a takzhe, ispol'zuya dannye
bematistov - lyudei special'noi professii, izmeryavshih rasstoyaniya
shagami. Teper' ostalos' reshit' proporciyu
km. Ee Eratosfen akkuratno vychislyaet, ishodya
iz srednego vremeni dvizheniya verblyuzh'ih karavanov, regulyarno
hodivshih mezhdu dvumya gorodami, a takzhe, ispol'zuya dannye
bematistov - lyudei special'noi professii, izmeryavshih rasstoyaniya
shagami. Teper' ostalos' reshit' proporciyu
![]() , poluchiv dlinu okruzhnosti (t.e., dlinu
zemnogo merediana)
, poluchiv dlinu okruzhnosti (t.e., dlinu
zemnogo merediana)
![]() km. Togda radius Zemli
km. Togda radius Zemli ![]() raven
raven
![]() , eto primerno
, eto primerno ![]() km. To, chto dlina zemnogo merediana
vyrazhaetsya stol' kruglym chislom v
km. To, chto dlina zemnogo merediana
vyrazhaetsya stol' kruglym chislom v ![]() km., ne udivitel'no,
esli vspomnit', chto edinica dliny v 1 metr i byla vvedena (vo
Francii v konce 18 veka), kak odna sorokamillionnaya chast'
okruzhnosti Zemli (po opredeleniyu !). Eratosfen, konechno,
ispol'zoval druguyu edinicu izmereniya - stadii (okolo 200
m). Stadiev bylo neskol'ko: egipetskii, grecheskii, vavilonskii, i
kakim iz nih pol'zovalsya Eratosfen - neizvestno. Poetomu trudno
sudit' navernyaka o tochnosti ego izmereniya. Krome togo, neizbezhnaya
oshibka voznikala v silu geograficheskogo polozheniya dvuh gorodov.
Eratosfen rassuzhdal tak: esli goroda nahodyatsya na odnom merediane
(t.e., Aleksandriya raspolozhena v tochnosti k severu ot Sieny), to
polden' v nih nastupaet odnovremenno. Poetomu, sdelav izmereniya vo
vremya naivysshego polozheniya Solnca v kazhdom gorode, my dolzhny
poluchit' pravil'nyi rezul'tat. No na samom dele Aleksandriya i
Siena - daleko ne na odnom merediane. Seichas v etom legko
ubedit'sya, vzglyanuv na kartu, no u Eratosfena takoi vozmozhnosti ne
bylo, on kak raz i rabotal nad sostavleniem pervyh kart. Poetomu
ego metod (absolyutno vernyi !) privel k oshibke v opredelenii
radiusa Zemli. Tem ne menee, mnogie issledovateli uvereny, chto
tochnost' izmereniya Eratosfena byla vysoka, i chto on oshibsya menee,
chem na
km., ne udivitel'no,
esli vspomnit', chto edinica dliny v 1 metr i byla vvedena (vo
Francii v konce 18 veka), kak odna sorokamillionnaya chast'
okruzhnosti Zemli (po opredeleniyu !). Eratosfen, konechno,
ispol'zoval druguyu edinicu izmereniya - stadii (okolo 200
m). Stadiev bylo neskol'ko: egipetskii, grecheskii, vavilonskii, i
kakim iz nih pol'zovalsya Eratosfen - neizvestno. Poetomu trudno
sudit' navernyaka o tochnosti ego izmereniya. Krome togo, neizbezhnaya
oshibka voznikala v silu geograficheskogo polozheniya dvuh gorodov.
Eratosfen rassuzhdal tak: esli goroda nahodyatsya na odnom merediane
(t.e., Aleksandriya raspolozhena v tochnosti k severu ot Sieny), to
polden' v nih nastupaet odnovremenno. Poetomu, sdelav izmereniya vo
vremya naivysshego polozheniya Solnca v kazhdom gorode, my dolzhny
poluchit' pravil'nyi rezul'tat. No na samom dele Aleksandriya i
Siena - daleko ne na odnom merediane. Seichas v etom legko
ubedit'sya, vzglyanuv na kartu, no u Eratosfena takoi vozmozhnosti ne
bylo, on kak raz i rabotal nad sostavleniem pervyh kart. Poetomu
ego metod (absolyutno vernyi !) privel k oshibke v opredelenii
radiusa Zemli. Tem ne menee, mnogie issledovateli uvereny, chto
tochnost' izmereniya Eratosfena byla vysoka, i chto on oshibsya menee,
chem na ![]() . Esli eto tak, to uluchshit' etot rezul'tat
chelovechestvo smoglo tol'ko cherez 2 tysyachi let, v seredine 19 veka.
Nad etim trudilas' gruppa uchenyh vo Francii i ekspediciya
V.Ya.Struve v Rossii. Dazhe v epohu velikih geograficheskih otkrytii,
v 16 veke, lyudi ne smogli dostich' rezul'tata Eratosfena, i
pol'zovalis' nevernym znacheniem dliny zemnoi okruzhnosti v 37.000
km. Ni Kolumb, ni Magellan ne znali, kakovy istinnye razmery
Zemli, i kakie rasstoyaniya im pridetsya preodolevat'. Oni-to
schitali, chto dlina ekvatora na 3 tysyachi km. men'she, chem na samom
dele. Znali by - mozhet i ne poplyli by.
. Esli eto tak, to uluchshit' etot rezul'tat
chelovechestvo smoglo tol'ko cherez 2 tysyachi let, v seredine 19 veka.
Nad etim trudilas' gruppa uchenyh vo Francii i ekspediciya
V.Ya.Struve v Rossii. Dazhe v epohu velikih geograficheskih otkrytii,
v 16 veke, lyudi ne smogli dostich' rezul'tata Eratosfena, i
pol'zovalis' nevernym znacheniem dliny zemnoi okruzhnosti v 37.000
km. Ni Kolumb, ni Magellan ne znali, kakovy istinnye razmery
Zemli, i kakie rasstoyaniya im pridetsya preodolevat'. Oni-to
schitali, chto dlina ekvatora na 3 tysyachi km. men'she, chem na samom
dele. Znali by - mozhet i ne poplyli by.
V chem prichina stol' vysokoi
tochnosti metoda Eratosfena (konechno, esli on pol'zovalsya nuzhnym
stadiem) ?
Do nego izmereniya byli lokal'nymi, na rasstoyaniyah, obozrimyh
chelovecheskim glazom, t.e., ne bolee 100 km. Takovy, naprimer,
sposoby v uprazhneniyah 1 i 2. Pri etom neizbezhny oshibki
iz-za rel'efa mestnosti, atmosfernyh yavlenii, i t.d.
Chtoby dobit'sya bol'shei tochnosti, nuzhno provodit' izmereniya
global'no, na rasstoyaniyah, sravnimyh s radiusom Zemli. Rasstoyanie
v ![]() km. mezhdu Aleksandriei i Sienoi okazalos' vpolne
dostatochnym.
km. mezhdu Aleksandriei i Sienoi okazalos' vpolne
dostatochnym.
Uprazhnenie 1. Kak vychislit' radius Zemli po sleduyushim dannym: s gory vysotoi 500 m. prosmatrivayutsya okrestnosti na rasstoyanii 80 km.?
Uprazhnenie 2. Kak vychislit' radius Zemli po sleduyushim dannym: korabl' vysotoi 20 m., otplyv ot berega na 16 km., polnost'yu ischezaet iz vida ?.
Uprazhnenie 3. Dva druga - odin v Moskve, drugoi - v Tule,
berut po metrovomu shestu i stavyat ih vertikal'no. V moment, v
techenie dnya, kogda ten' ot shesta dostigaet naimen'shei dliny,
kazhdyi iz nih izmeryaet dlinu teni. V Moskve poluchilos' ![]() sm., a
v Tule -
sm., a
v Tule - ![]() sm. Vyrazite radius Zemli cherez
sm. Vyrazite radius Zemli cherez ![]() i
i ![]() . Goroda
raspolozheny na odnom meridiane na rasstoyanii 185 km.
. Goroda
raspolozheny na odnom meridiane na rasstoyanii 185 km.
Kak vidno iz uprazhneniya 3, opyt Eratosfena mozhno prodelat' i v nashih shirotah, gde Solnce nikogda ne byvaet v zenite. Pravda, dlya etogo nuzhny dve tochki obyazatel'no na odnom merediane. Esli zhe povtorit' opyt Eratosfena dlya Aleksandrii i Sieny, i pri etom sdelat' izmereniya v etih gorodah odnovremenno (seichas dlya etogo est' tehnicheskie vozmozhnosti), to my poluchim vernyi otvet, pri etom budet ne vazhno, na kakom merediane nahoditsya Siena (pochemu ?).
 Pamyatnik Aristarhu-Samosskomu v Salonikah |
Vychislenie Aristarha mozhno uslovno razbit' na tri shaga. Kazhdyi shag
svoditsya k prostoi geometricheskoi zadache. Pervye dva shaga sovsem
elementarny, tretii - chut' poslozhnee. V geometricheskih
postroeniyah my budem oboznachat' cherez ![]() i
i ![]() centy Zemli,
Solnca i Luny sootvetstvenno, a cherez
centy Zemli,
Solnca i Luny sootvetstvenno, a cherez
![]() i
i ![]() -
ih radiusy. Vse nebesnye tela budem schitat' sharami, a ih orbity -
okruzhnostyami, kak i schital sam Aristarh (hotya, kak my teper'
znaem, eto ne sovsem tak). My nachinaem s pervogo shaga, i dlya etogo
nemnogo ponablyudaem za Lunoi.
-
ih radiusy. Vse nebesnye tela budem schitat' sharami, a ih orbity -
okruzhnostyami, kak i schital sam Aristarh (hotya, kak my teper'
znaem, eto ne sovsem tak). My nachinaem s pervogo shaga, i dlya etogo
nemnogo ponablyudaem za Lunoi.
Shag 1. Vo skol'ko raz Solnce dal'she, chem Luna ?
Kak izvestno, Luna svetit otrazhennym solnechnym svetom. Esli vzyat' shar, i posvetit' na nego so storony bol'shim prozhektorom, to v lyubom polozhenii osveshennoi okazhetsya rovno polovina poverhnosti shara. Granica osveshennoi polusfery - okruzhnost', lezhashaya v ploskosti, perpendikulyarnoi lucham sveta. Takim obrazom, Solnce vsegda osveshaet rovno polovinu poverhnosti Luny. Vidimaya nam forma Luny zavisit ot togo, kak raspolozhena eta osveshennaya polovina. Pri novolunii, kogda Luna vovse ne vidna na nebe, Solnce osveshaet ee obratnuyu storonu. Zatem osveshennaya polusfera postepenno povorachivaetsya v storonu Zemli. My nachinaem videt' tonkii serp, zatem - mesyac ("rastushaya Luna"), dalee - polukrug (eta faza Luny nazyvaetsya "kvadraturoi"). Zatem den' oto dnya (vernee, noch' ot nochi) polukrug dorastaet do polnoi Luny. Potom nachinaetsya obratnyi process: osveshennaya polusfera ot nas otvorachivaetsya. Luna "stareet", postepenno prevrashayas' v mesyac, povernutyi k nam levoi storonoi, podobno bukve "C", i, nakonec, v noch' novoluniya ischezaet. Period ot odnogo novoluniya do drugogo dlitsya primerno chetyre nedeli. Za eto vremya Luna sovershaet polnyi oborot vokrug Zemli. Ot novoluniya do poloviny Luny prohodit chetvert' perioda, otsyuda i nazvanie "kvadratura".
 Ris. 3. |
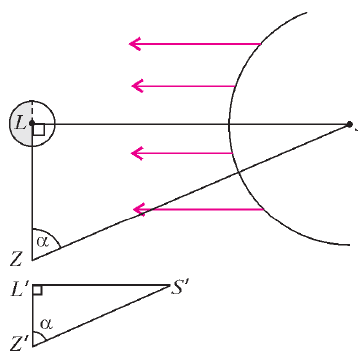
Itak, izmeriv ugol ![]() mezhdu luchami
mezhdu luchami ![]() i
i ![]() vo vremya
kvadratury, Aristarh vychislyaet otnoshenie rasstoyanii do Luny i do
Solnca. Kak odnovremenno zastat' Solnce i Lunu na nebosvode ? Eto
mozhno sdelat' rannim utrom, kogda v yasnuyu pogodu vidny oba
nebesnyh tela. Slozhnost' voznikaet po drugomu, neozhidannomu,
povodu. Vo vremena Aristarha ne bylo kosinusov. Pervye ponyatiya
trigonometrii poyavyatsya pozzhe, v rabotah Apolloniya i Arhimeda. No
Aristarh znal, chto takoe podobnye treugol'niki, i etogo bylo
dostatochno. Nachertiv malen'kii pryamougol'nyi treugol'nik
vo vremya
kvadratury, Aristarh vychislyaet otnoshenie rasstoyanii do Luny i do
Solnca. Kak odnovremenno zastat' Solnce i Lunu na nebosvode ? Eto
mozhno sdelat' rannim utrom, kogda v yasnuyu pogodu vidny oba
nebesnyh tela. Slozhnost' voznikaet po drugomu, neozhidannomu,
povodu. Vo vremena Aristarha ne bylo kosinusov. Pervye ponyatiya
trigonometrii poyavyatsya pozzhe, v rabotah Apolloniya i Arhimeda. No
Aristarh znal, chto takoe podobnye treugol'niki, i etogo bylo
dostatochno. Nachertiv malen'kii pryamougol'nyi treugol'nik ![]() s tem zhe ostrym uglov
s tem zhe ostrym uglov
![]() , i
izmeriv ego storony, poluchaem, chto
, i
izmeriv ego storony, poluchaem, chto
![]() , i eto otnoshenie primerno ravno
, i eto otnoshenie primerno ravno
![]() . Poluchaetsya, chto Solnce v 400 raz dal'she ot Zemli,
chem Luna. Etu konstantu - otnoshenie rasstoyanii ot Zemli do Solnca
i ot Zemli do Luny, my
my budem oboznachat' bukvoi
. Poluchaetsya, chto Solnce v 400 raz dal'she ot Zemli,
chem Luna. Etu konstantu - otnoshenie rasstoyanii ot Zemli do Solnca
i ot Zemli do Luny, my
my budem oboznachat' bukvoi ![]() . Itak, my nashli, chto
. Itak, my nashli, chto
![]() .
.
Shag 2. Vo skol'ko raz Solnce bol'she Luny ?
Dlya togo, chtoby naiti otnoshenie radiusov Solnca i Luny, Aristarh privlekaet Solnechnye zatmeniya (ris.4). Oni proishodyat, kogda Luna zagorazhivaet Solnce. Pri chastichnom, ili kak govoryat astronomy, chastnom zatmenii Luna lish' prohodit po disku Solnca, ne zakryvaya ego polnost'yu. Poroi takoe zatmenie dazhe nel'zya razglyadet' nevooruzhennym glazom, Solnce svetit kak v obychnyi den'. Lish' skvoz' sil'noe zatemnenie, naprimer, zakopchenoe steklo, vidno, kak chast' solnechnogo diska zakryta chernym krugom.
 Ris. 4. |
Gorazdo rezhe proishodit polnoe zatmenie, kogda Luna na neskol'ko
minut polnost'yu zakryvaet solnechnyi disk. V eto vremya stanovitsya
temno, na nebe poyavlyayutsya zvezdy. Zatmeniya navodili uzhas na
drevnih lyudei, schitalis' predvestnikami tragedii. Solnechnoe
zatmenie nablyudaetsya po-raznomu v raznyh chastyah Zemli. Vo vremya
polnogo zatmeniya na poverhnosti Zemli voznikaet ten' ot Luny -
krug, diametr kotorogo ne prevoshodit 270 km. Lish' v teh raionah
zemnogo shara, po kotorym prohodit eta ten', mozhno nablyudat' polnoe
zatmenie. Poetomu v odnom i tom zhe meste polnoe zatmenie
proishodit kraine redko - v srednem raz v 200-300 let. Aristarhu
povezlo - on smog nablyudat' polnoe solnechnoe zatmenie
sobstvennymi glazami. Na bezoblachnom nebe Solnce postepenno nachalo
tusknet' i umen'shat'sya v razmerah, ustanovilis' sumerki. Na
neskol'ko mgnovenii Solnce ischezlo. Potom proglyanul pervyi luch
sveta, solnechnyi disk stal rasti, i vskore Solnce zasvetilo v
polnuyu silu. Pochemu zatmenie dlitsya stol' korotkoe vremya ?
Aristarh otvechaet na etot vopros: prichina v tom, chto Luna imeet te
zhe vidimye razmery na nebe, chto i Solnce. Chto eto znachit ?
Provedem ploskost' cherez centry Zemli, Solnca i Luny. Poluchivsheesya
sechenie izobrazheno na risunke 5 (a). Ugol mezhdu kasatel'nymi,
provedenymi iz tochki ![]() k okruzhnosti Luny nazyvaetsya
uglovym razmerom Luny, ili ee uglovym diametrom. Tak zhe
opredelyaetsya uglovoi razmer Solnca. Esli uglovye diametry Solnca i
Luny sovpadayut, to oni imeyut odinakovye vidimye razmery na nebe,
a
pri zatmenii Luna deistvitel'no polnost'yu
zagorazhivaet Solnce (ris. 5 (b)), no lish' na mgnovenie, kogda
sovpadut luchi
k okruzhnosti Luny nazyvaetsya
uglovym razmerom Luny, ili ee uglovym diametrom. Tak zhe
opredelyaetsya uglovoi razmer Solnca. Esli uglovye diametry Solnca i
Luny sovpadayut, to oni imeyut odinakovye vidimye razmery na nebe,
a
pri zatmenii Luna deistvitel'no polnost'yu
zagorazhivaet Solnce (ris. 5 (b)), no lish' na mgnovenie, kogda
sovpadut luchi ![]() i
i ![]() . Na fotografii polnogo solnechnogo
zatmeniya (sm. ris. 4) yasno vidno ravenstvo razmerov.
. Na fotografii polnogo solnechnogo
zatmeniya (sm. ris. 4) yasno vidno ravenstvo razmerov.
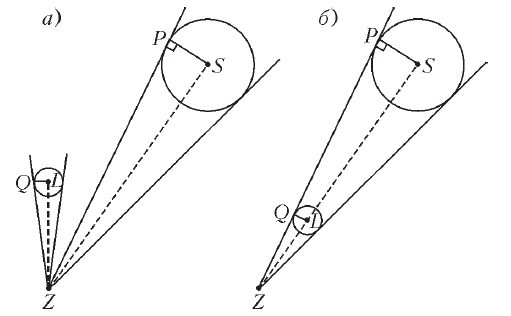 Ris. 5. |
Vyvod Aristarha okazalsya porazitel'no tochen ! V real'nosti srednie
uglovye diametry Solnca i Luny otlichayutsya vsego na ![]() . My
vynuzhdeny govorit' o srednih diametrah, poskol'ku oni menyayutsya v
techenie goda, tak kak planety dvizhutsya ne po okruzhnostyam, a po
ellipsam.
. My
vynuzhdeny govorit' o srednih diametrah, poskol'ku oni menyayutsya v
techenie goda, tak kak planety dvizhutsya ne po okruzhnostyam, a po
ellipsam.
Soediniv centr Zemli ![]() s centrami Solnca
s centrami Solnca ![]() i Luny
i Luny ![]() , a takzhe
c tochkami kasaniya
, a takzhe
c tochkami kasaniya ![]() i
i ![]() , poluchim dva pryamougol'nyh
treugol'nika
, poluchim dva pryamougol'nyh
treugol'nika ![]() i
i ![]() (ris. 5 (a)). Oni podobny, poskol'ku u
nih est' para ravnyh ostryh uglov
(ris. 5 (a)). Oni podobny, poskol'ku u
nih est' para ravnyh ostryh uglov
![]() .
Sledovatel'no,
.
Sledovatel'no,
![]() . Takim obrazom, otnoshenie radiusov Solnca i
Luny ravno otnosheniyu rasstoyanii ot ih centrov do centra Zemli.
Itak,
. Takim obrazom, otnoshenie radiusov Solnca i
Luny ravno otnosheniyu rasstoyanii ot ih centrov do centra Zemli.
Itak,
![]() . Nesmotrya
na to, chto ih vidimye razmery ravny, Solnce okazalos' bol'she Luny
v
. Nesmotrya
na to, chto ih vidimye razmery ravny, Solnce okazalos' bol'she Luny
v ![]() raz !
raz !
Ravenstvo uglovyh razmerov Luny i Solnca - schastlivoe sovpadenie. Ono ne vytekaet iz zakonov mehaniki. U mnogih planet Solnechnoi sistemy est' sputniki: u Marsa ih dva, u Yupitera - chetyre (i eshe neskol'ko desyatkov melkih), i vse oni imeyut raznye uglovye razmery, ne sovpadayushie s solnechnym.
Teper' my pristupaem k reshayushemu i samomu slozhnomu shagu.
Shag 3. Vychislenie razmerov Solnca i Luny i rasstoyanii do nih.
Itak, nam izvestno otnoshenie razmerov Solnca i Luny, i otnoshenie
ih rasstoyanii do Zemli. Eta informaciya otnositel'na: ona
vosstanavlivaet kartinu okruzhayushego mira lish' s tochnost'yu do
podobiya. Mozhno udalit' Lunu i Solnce ot Zemli v 10 raz, uvelichiv
vo stol'ko zhe raz ih razmery, i vidimaya s Zemli kartina ostanetsya
takoi zhe. Chtoby naiti real'nye razmery nebesnyh tel, nado
sootnesti ih s kakim-to izvestnym razmerom.
No iz vseh astronomicheskih velichin Aristarhu poka
izvesten tol'ko radius zemnogo shara3 ![]() km.
Pomozhet li eto ? Hot' v
kakom-to iz vidimyh yavlenii, proishodyashih na nebe, poyavlyaetsya
radius Zemli ? Ne sluchaino govoryat "nebo i zemlya", imeya v vidu
dve nesovmestnye veshi. I vse zhe, takoe yavlenie est'. Eto - lunnoe
zatmenie. S ego pomosh'yu, primeniv dovol'no hitroumnoe
geometricheskoe postroenie, Aristarh vychislyaet otnoshenie radiusa
Solnca k radiusu Zemli, i cep' zamykaetsya: teper' my odnovremenno
nahodim radius Luny, radius Solnca, a zaodno i rasstoyaniya ot Luny
i ot Solnca do Zemli.
km.
Pomozhet li eto ? Hot' v
kakom-to iz vidimyh yavlenii, proishodyashih na nebe, poyavlyaetsya
radius Zemli ? Ne sluchaino govoryat "nebo i zemlya", imeya v vidu
dve nesovmestnye veshi. I vse zhe, takoe yavlenie est'. Eto - lunnoe
zatmenie. S ego pomosh'yu, primeniv dovol'no hitroumnoe
geometricheskoe postroenie, Aristarh vychislyaet otnoshenie radiusa
Solnca k radiusu Zemli, i cep' zamykaetsya: teper' my odnovremenno
nahodim radius Luny, radius Solnca, a zaodno i rasstoyaniya ot Luny
i ot Solnca do Zemli.
 Ris. 6. |
Uprazhnenie 4. Na ploskosti dana duga okruzhnosti. S pomosh'yu cirkulya i lineiki postroite otrezok, ravnyi ee radiusu.
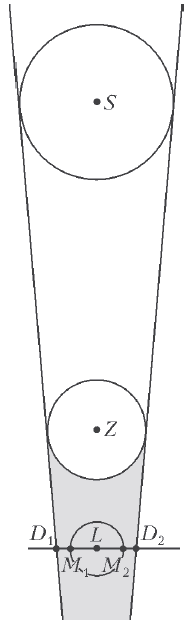 Ris. 7. |
Zadacha 1. Dany tri okruzhnosti s centrami
![]() i
i ![]() , lezhashimi na odnoi pryamoi. Otrezok
, lezhashimi na odnoi pryamoi. Otrezok ![]() ,
prohodyashii cherez
,
prohodyashii cherez ![]() , perpendikulyaren pryamoi
, perpendikulyaren pryamoi ![]() , a ego koncy
lezhat na obshih vneshnih kasatel'nyh k pervoi i vtoroi okruzhnostyam.
Izvestno, chto otnoshenie otrezka
, a ego koncy
lezhat na obshih vneshnih kasatel'nyh k pervoi i vtoroi okruzhnostyam.
Izvestno, chto otnoshenie otrezka ![]() k diametru tret'ei
okruzhnosti ravno
k diametru tret'ei
okruzhnosti ravno ![]() , a otnoshenie diametrov pervoi i tret'ei
okruzhnosti ravno
, a otnoshenie diametrov pervoi i tret'ei
okruzhnosti ravno
![]() . Naiti otnoshenie
diametrov pervoi i vtoroi okruzhnosti.
. Naiti otnoshenie
diametrov pervoi i vtoroi okruzhnosti.
Esli reshit' etu zadachu, to budet naideno otnoshenie radiusov Solnca
i Zemli. Znachit, budet naiden radius Solnca, a s nim i Luny. No
reshit' ee ne udastsya. Mozhete poprobovat' - v zadache ne dostaet
odnogo dannogo. Naprimer, ugla mezhdu obshimi vneshnimi kasatel'nymi
k pervym dvum okruzhnostyam. No dazhe esli etot ugol byl by izvesten,
reshenie budet ispol'zovat' trigonometriyu, kotoruyu Aristarh ne
znal
(my formuliruem sootvetstvuyushuyu zadachu v uprazhnenii 6).
On nahodit bolee prostoi vyhod. Provedem diametr ![]() pervoi
okruzhnosti i diametr
pervoi
okruzhnosti i diametr ![]() vtoroi, oba - parallel'nye otrezku
vtoroi, oba - parallel'nye otrezku
![]() . Pust'
. Pust' ![]() i
i ![]() - tochki peresecheniya otrezka
- tochki peresecheniya otrezka
![]() s pryamymi
s pryamymi ![]() i
i ![]() sootvetstvenno (ris. 8).
sootvetstvenno (ris. 8).
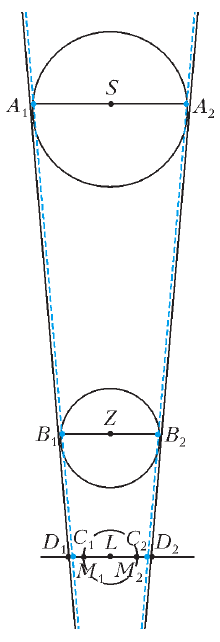 Ris. 8. |
Zadacha 1'. Na bokovyh storonah ![]() i
i
![]() trapecii
trapecii
![]() vzyaty tochki
vzyaty tochki ![]() i
i ![]() tak,
chto otrezok
tak,
chto otrezok ![]() parallelen osnovaniyam. Pust'
parallelen osnovaniyam. Pust' ![]() i
i ![]() -
serediny otrezkov
-
serediny otrezkov
![]() i
i ![]() sootvetstvenno. Na
osnovanii
sootvetstvenno. Na
osnovanii ![]() lezhit otrezok
lezhit otrezok ![]() s seredinoi
s seredinoi ![]() .
Izvestno, chto
.
Izvestno, chto
![]() i
i
![]() . Naiti
. Naiti
![]() .
.
Reshenie. Tak kak
![]() , to
, to
![]() ,
a znachit treugol'niki
,
a znachit treugol'niki ![]() i
i ![]() podobny s koefficientom
podobny s koefficientom
![]() . Sledovatel'no,
. Sledovatel'no,
![]() , i poetomu tochka
, i poetomu tochka ![]() lezhit na otrezke
lezhit na otrezke
![]() . Analogichno,
. Analogichno, ![]() lezhit na otrezke
lezhit na otrezke ![]() (ris. 9). Tak
kak
(ris. 9). Tak
kak
![]() i
i
![]() , to
, to
![]() .
.
Dalee, treugol'niki ![]() i
i ![]() podobny. Ih
koefficient podobiya raven
podobny. Ih
koefficient podobiya raven
![]() . Sledovatel'no,
. Sledovatel'no,
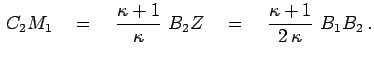
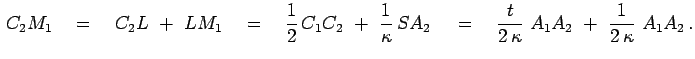
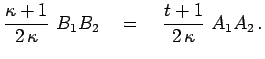
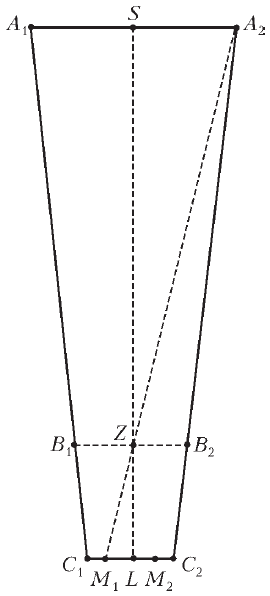 Ris. 9. |
Teper' rasstoyaniya ot Zemli do Luny i do Solnca vychislyayutsya v odin
shag, eto mozhet byt' sdelano s pomosh'yu uglovogo diametra. Uglovoi
diametr ![]() Solnca i Luny raven primerno polgradusa (esli
byt' sovsem tochnym,
Solnca i Luny raven primerno polgradusa (esli
byt' sovsem tochnym, ![]() ). Kak drevnie astronomy ego
izmeryali, ob etom rech' vperedi. Opustiv kasatel'nuyu
). Kak drevnie astronomy ego
izmeryali, ob etom rech' vperedi. Opustiv kasatel'nuyu ![]() na
okruzhnost' Luny, poluchaem pryamougol'nyi treugol'nik
na
okruzhnost' Luny, poluchaem pryamougol'nyi treugol'nik ![]() s ostrym
uglom
s ostrym
uglom
![]() (ris. 10).
(ris. 10).
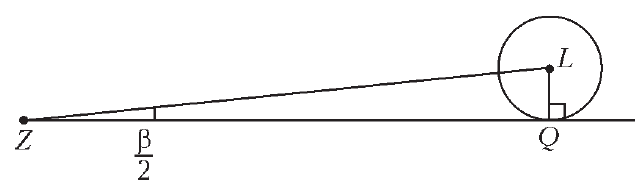 Ris. 10. |
Iz nego nahodim
![]() , chto primerno ravno
, chto primerno ravno
![]() , ili
, ili ![]() . Analogichno, rasstoyanie do Solnca ravno
. Analogichno, rasstoyanie do Solnca ravno
![]() .
.
Vse. Razmery Solnca i Luny i rasstoyaniya da nih naideny.
Uprazhnenie 5. Dokazhite, chto pryamye
![]() i dve obshie
vneshnie kasatel'nye k pervoi i vtoroi okruzhnostyam (ris. 8)
peresekayutsya v odnoi tochke.
i dve obshie
vneshnie kasatel'nye k pervoi i vtoroi okruzhnostyam (ris. 8)
peresekayutsya v odnoi tochke.
Uprazhnenie 6. Reshite zadachu 1, esli dopolnitel'no izvesten ugol mezhdu kasatel'nymi mezhdu pervoi i vtoroi okruzhnost'yu.
Uprazhnenie 7. Solnechnoe zatmenie mozhet nablyudat'sya v odnih chastyah zemnogo shara i ne nablyudat'sya drugih. A lunnoe zatmenie ?
Uprazhnenie 8. Dokazhite, chto solnechnoe zatmenie mozhet nablyudat'sya tol'ko vo vremya novoluniya, a lunnoe zatmenie - tol'ko vo vremya polnoluniya.
Uprazhnenie 9. Chto proishodit na Lune, kogda na Zemle proishodit lunnoe zatmenie ?
Na samom dele vse bylo neskol'ko slozhnee.
Geometriya tol'ko formirovalas', i mnogie privychnye dlya nas, eshe s vos'mogo klassa shkoly,
veshi byli v to vremya sovsem ne ochevidny. Aristarhu potrebovalos' napisat' celuyu knigu,
chtoby izlozhit' to, chto my izlozhili na treh stranicah. I s eksperimental'nymi
izmereniyami tozhe vse bylo neprosto. Vo-pervyh, Aristarh oshibsya s
izmereniem diametra zemnoi teni vo vremya lunnogo zatmeniya, poluchiv otnoshenie ![]() , vmesto
, vmesto
![]() . Krome togo, on, vrode by, ishodil iz nevernogo
znacheniya ugla
. Krome togo, on, vrode by, ishodil iz nevernogo
znacheniya ugla ![]() - uglovogo diametra Solnca, schitaya ego ravnym
- uglovogo diametra Solnca, schitaya ego ravnym ![]() .
No eta versiya spornaya: Arhimed v svoem traktate "Psammit"
pishet, chto, naprotiv, Aristarh pol'zovalsya pochti pravil'nym
znacheniem v
.
No eta versiya spornaya: Arhimed v svoem traktate "Psammit"
pishet, chto, naprotiv, Aristarh pol'zovalsya pochti pravil'nym
znacheniem v ![]() . Odnako, samaya uzhasnaya oshibka proizoshla na
pervom shage, pri vychislenii parametra
. Odnako, samaya uzhasnaya oshibka proizoshla na
pervom shage, pri vychislenii parametra ![]() - otnosheniya
rasstoyanii ot Zemli do Solnca i do Luny. Vmesto
- otnosheniya
rasstoyanii ot Zemli do Solnca i do Luny. Vmesto
![]() u
Aristarha poluchilos'
u
Aristarha poluchilos'
![]() . Kak mozhno bylo oshibit'sya
bolee, chem v 20 raz ? Obratimsya eshe raz k shagu 1, ris 3. Dlya togo,
chtoby naiti otnoshenie
. Kak mozhno bylo oshibit'sya
bolee, chem v 20 raz ? Obratimsya eshe raz k shagu 1, ris 3. Dlya togo,
chtoby naiti otnoshenie
![]() Aristarh
izmeril ugol
Aristarh
izmeril ugol
![]() , i togda
, i togda
![]() . Naprimer, esli ugol
. Naprimer, esli ugol ![]() byl
by raven
byl
by raven ![]() , to my poluchili by
, to my poluchili by ![]() , i Solnce bylo by
vdvoe dal'she ot Zemli, chem Luna. No rezul'tat izmereniya okazalsya
neozhidannym: ugol
, i Solnce bylo by
vdvoe dal'she ot Zemli, chem Luna. No rezul'tat izmereniya okazalsya
neozhidannym: ugol ![]() poluchalsya pochti pryamym. Eto oznachalo,
chto katet
poluchalsya pochti pryamym. Eto oznachalo,
chto katet ![]() vo mnogo raz prevoshodit
vo mnogo raz prevoshodit ![]() . U Aristarha
poluchilos'
. U Aristarha
poluchilos'
![]() , i togda
, i togda
![]() (napomnim, chto vse vychisleniya u nas -
priblizhennye). Istinnoe znachenie ugla
(napomnim, chto vse vychisleniya u nas -
priblizhennye). Istinnoe znachenie ugla
![]() , i
, i
![]() . Tak
pogreshnost' izmereniya menee, chem v
. Tak
pogreshnost' izmereniya menee, chem v ![]() , privela k oshibke v
, privela k oshibke v ![]() raz ! Zavershiv vychisleniya, Aristarh prihodit k vyvodu, chto radius
Solnca raven
raz ! Zavershiv vychisleniya, Aristarh prihodit k vyvodu, chto radius
Solnca raven ![]() radiusov Zemli (vmesto
radiusov Zemli (vmesto ![]() ).
).
Oshibki byli neizbezhny, uchityvaya nesovershennye izmeritel'nye
pribory togo vremeni. Vazhnee to, chto metod okazalsya pravil'nym.
Vskore (po istoricheskim merkam, t.e., primerno cherez 100 let)
vydayushiisya astronom antichnosti Gipparh (190 - ok. 120 do n. e.)
ustranit vse netochnosti i, sleduya metodu Aristarha, vychislit
pravil'nye razmery Solnca i Luny. Vozmozhno, oshibka Aristarha
okazalas' v rezul'tate dazhe poleznoi. Do nego gospodstvovalo
mnenie, chto Solnce i Luna libo vovse imeyut odinakovye razmery (kak
i kazhetsya zemnomu nalyudatelyu), libo otlichayutsya nesil'no. Dazhe
otlichie v ![]() raz udivilo sovremennikov. Poetomu, ne isklyucheno,
chto, naidi Aristarh pravil'noe otnoshenie
raz udivilo sovremennikov. Poetomu, ne isklyucheno,
chto, naidi Aristarh pravil'noe otnoshenie
![]() ,
v eto nikto by ne poveril, a mozhet byt', i sam uchenyi otkazalsya
by ot svoego metoda, sochtya rezul'tat nesuraznym. Izvestnyi princip
glasit, chto
geometriya - eto iskusstvo horosho rassuzhdat' na ploho vypolnennyh chertezhah.
Perefraziruya, mozhno skazat', chto nauka v celom - eto iskusstvo delat' vernye vyvody iz
netochnyh, ili dazhe oshibochnyh, nablyudenii. I Aristarh takoi vyvod sdelal !
Za 17 vekov do Kopernika on ponyal, chto v centre mira nahoditsya ne
Zemlya, a Solnce. Tak vpervye poyavilas' geliocentricheskaya model' i
ponyatie Solnechnoi sistemy.
,
v eto nikto by ne poveril, a mozhet byt', i sam uchenyi otkazalsya
by ot svoego metoda, sochtya rezul'tat nesuraznym. Izvestnyi princip
glasit, chto
geometriya - eto iskusstvo horosho rassuzhdat' na ploho vypolnennyh chertezhah.
Perefraziruya, mozhno skazat', chto nauka v celom - eto iskusstvo delat' vernye vyvody iz
netochnyh, ili dazhe oshibochnyh, nablyudenii. I Aristarh takoi vyvod sdelal !
Za 17 vekov do Kopernika on ponyal, chto v centre mira nahoditsya ne
Zemlya, a Solnce. Tak vpervye poyavilas' geliocentricheskaya model' i
ponyatie Solnechnoi sistemy.
Gospodstvovavshee v Drevnem Mire predstavlenie ob ustroistve
Vselennoi, znakomoe nam po urokam istorii, zaklyuchalos' v tom, chto
v centre mira - nepodvizhnaya Zemlya, vokrug nee po krugovym orbitam
vrashayutsya 7 planet, vklyuchaya Lunu i Solnce (kotoroe tozhe
schitalos' planetoi). Zavershaetsya vse nebesnoi sferoi s
prikreplennymi k nei zvezdami. Sfera
vrashaetsya vokrug Zemli, delaya polnyi oborot za 24 chasa. So vremenem v etu model' mnogokratno
vnosilis' ispravleniya. Tak, stali schitat', chto nebesnaya sfera
nepodvizhna, a Zemlya vrashaetsya vokrug svoei osi. Zatem stali
ispravlyat' traektorii dvizheniya planet: krugi zamenili cikloidami,
t.e., liniyami, kotorye opisyvayut tochki okruzhnosti pri ee dvizhenii
po drugoi okruzhnosti (ob etih zamechatel'nyh liniyah mozhno prochitat'
v
knigah G.N.Bermana "Cikloida",
A.I.Markushevicha "Zamechatel'nye krivye", a takzhe v "Kvante":
stat'ya S.Verova "Tainy cikloidy" N8, 1975, i stat'ya
S.G.Gindikina "Zvezdnyi vek cikloidy", N6,1985). Cikloidy luchshe
soglasovyvalis' s rezul'tatami nablyudenii, v chastnosti, ob'yasnyali
"popyatnye" dvizheniya planet. Eto - geocentricheskaya
sistema mira, v centre kotoroi - Zemlya ("geo"). Vo II v. n.e.
ona prinyala okonchatel'nyi vid v knige "Al'magest" Klavdiya
Ptolemeya (87-165 n.e.), vydayushegosya grecheskogo astronoma, odnofamil'ca
egipetskih carei. So vremenem nekotorye cikloidy uslozhnyalis',
dobavlyalis' vse novye promezhutochnye okruzhnosti. No v celom
sistema Ptolemeya gospodstvovala okolo polutora tysyacheletii, do XVI
veka, do otkrytii Kopernika i Keplera. Ponachalu geocentricheskoi
modeli priderzhivalsya i Aristarh. Odnako, vychisliv, chto radius
Solnca v ![]() raz bol'she radiusa Zemli, on zadal prostoi vopros:
pochemu takoe bol'shoe Solnce dolzhno vrashat'sya vokrug takoi
malen'koi Zemli ? Ved' esli radius Solnca bol'she v
raz bol'she radiusa Zemli, on zadal prostoi vopros:
pochemu takoe bol'shoe Solnce dolzhno vrashat'sya vokrug takoi
malen'koi Zemli ? Ved' esli radius Solnca bol'she v ![]() raz, to
ego ob'em bol'she pochti v
raz, to
ego ob'em bol'she pochti v ![]() raz ! Znachit, v centre mira dolzhno
nahodit'sya Solnce. Vokrug nego vrashayutsya 6 planet, vklyuchaya
Zemlyu.4 A sed'maya planeta, Luna, vrashaetsya vokrug Zemli.
Tak vpervye poyavilas' geliocentricheskaya
sistema mira ("gelios" - Solnce). Uzhe sam Aristarh otmechal, chto takaya model' luchshe ob'yasnyaet vidimoe dvizhenie
planet po krugovym orbitam, luchshe soglasuetsya s rezul'tatami
nablyudenii. No ee ne prinyali ni uchenye, ni oficial'nye vlasti.
Aristarh byl obvinen v bezbozhii i podvergsya presledovaniyam. Iz
vseh astronomov antichnosti, tol'ko Selevk stal storonnikom novoi
modeli. Bol'she ee ne prinyal nikto, po krainei mere, u istorikov
net tverdyh svedenii na etot schet. Dazhe Arhimed i Gipparh,
pochitavshie Aristarha i razvivshie mnogie ego idei, ne reshilis'
postavit' Solnce v centr mira. Pochemu ?
raz ! Znachit, v centre mira dolzhno
nahodit'sya Solnce. Vokrug nego vrashayutsya 6 planet, vklyuchaya
Zemlyu.4 A sed'maya planeta, Luna, vrashaetsya vokrug Zemli.
Tak vpervye poyavilas' geliocentricheskaya
sistema mira ("gelios" - Solnce). Uzhe sam Aristarh otmechal, chto takaya model' luchshe ob'yasnyaet vidimoe dvizhenie
planet po krugovym orbitam, luchshe soglasuetsya s rezul'tatami
nablyudenii. No ee ne prinyali ni uchenye, ni oficial'nye vlasti.
Aristarh byl obvinen v bezbozhii i podvergsya presledovaniyam. Iz
vseh astronomov antichnosti, tol'ko Selevk stal storonnikom novoi
modeli. Bol'she ee ne prinyal nikto, po krainei mere, u istorikov
net tverdyh svedenii na etot schet. Dazhe Arhimed i Gipparh,
pochitavshie Aristarha i razvivshie mnogie ego idei, ne reshilis'
postavit' Solnce v centr mira. Pochemu ?
Kak zhe poluchilos', chto v techenii 17 vekov uchenye ne prinimali
prostoi i logichnoi sistemy mira, predlozhennoi Aristarhom ? I eto
nesmotrya na to, chto oficial'no priznannaya geocentricheskaya sistema
Ptolemeya chasto davala sboi, ne soglasuyas' s rezul'tatami
nablyudenii za planetami i za zvezdami. Prihodilos' dobavlyat' vse
novye okruzhnosti (tak nazyvaemye, vlozhennye cikly) dlya
"pravil'nogo" opisaniya dvizheniya planet. Samogo Ptolemeya
trudnosti ne pugali, on pisal: "K chemu udivlyat'sya slozhnomu
dvizheniyu nebesnyh tel, esli ih sushnost' nam neizvestna ?" Odnako,
uzhe k XIII veku etih okruzhnostei nakopilos' 75 ! Model' stala
stol' gromozdkoi, chto nachali razdavat'sya ostorozhnye vozrazheniya:
neuzheli mir v samom dele ustroen tak slozhno ? Shiroko izvesten
sluchai s Al'fonsom X (1226-1284), korolem Kastil'i i Leona,
gosudarstva, zanimavshego chast' sovremennoi Ispanii. On,
pokrovitel' nauk i iskusstv, sobravshii pri svoem dvore pyat'desyat
luchshih astronomov mira, na odnoi iz nauchnyh besed obmolvilsya, chto
"esli by pri sotvorenii mira Gospod' okazal mne chest' i sprosil
moego soveta, mnogoe bylo by ustroeno proshe." Podobnaya derzost'
ne proshalas' dazhe korolyam: Al'fons byl nizlozhen i otpravlen v
monastyr'.5 No
somneniya ostalis'. Chast' iz nih mozhno bylo by razreshit', postaviv
Solnce v centr Vselennoi i prinyav sistemu Aristarha. Ego trudy
byli horosho izvestny. Odnako, eshe mnogo vekov nikto iz uchenyh ne
reshalsya na takoi shag. Prichiny byli ne tol'ko v strahe pered
vlastyami i oficial'noi cerkov'yu, kotoraya schitala teoriyu Ptolemeya
edinstvenno vernoi. I ne tol'ko v inertnosti chelovecheskogo
myshleniya: ne tak-to prosto priznat', chto nasha Zemlya - ne centr
mira, a lish' ryadovaya planeta. Vse-taki, dlya nastoyashego uchenogo ni
strah ni stereotipy - ne prepyatstviya na puti k istine.
Geliocenticheskaya sistema otvergalas' po vpolne nauchnym, mozhno dazhe
skazat', geometricheskim prichinam. Esli dopustit', chto Zemlya
vrashaetsya vokrug Solnca, to, ee traektoriya - okruzhnost' s
radiusom ravnym rasstoyaniyu ot Zemli do Solnca. Kak my znaem, eto
rasstoyanie ravno 23455 radiusov Zemli, t.e., bolee 150 millionov
kilometrov.
Znachit, Zemlya v techenie polugoda peremeshaetsya na 300 millionov kilometrov. Gigantskaya velichina !
No kartina zvezdnogo neba dlya zemnogo nablyudatelya pri etom
ostaetsya takoi zhe. Zemlya to priblizhaetsya, to udalyaetsya ot zvezd na
300 millionov kilometrov, no
ni vidimye rasstoyaniya mezhdu zvezdami (naprimer, forma sozvezdii),
ni ih yarkost' ne menyayutsya. Eto oznachaet, chto rasstoyaniya do zvezd
dolzhny byt' eshe v neskol'ko tysyach raz bol'she. To est', nebesnaya
sfera dolzhna imet' sovershenno nevoobrazimye razmery ! Eto, mezhdu
prochim, osoznaval i sam Aristarh, kotoryi pisal v svoei knige:
"Ob'em sfery nepodvizhnyh zvezd vo stol'ko raz bol'she ob'ema sfery
s radiusom Zemlya-Solnce, vo skol'ko raz ob'em poslednei bol'she
ob'ema zemnogo shara". T.e., po Aristarhu vyhodilo, chto
rasstoyaniya do zvezd ravno
![]() , eto bolee 3.5 trillionov
kilometrov (v real'nosti rasstoyanie ot Solnca do blizhaishei zvezdy
eshe primerno v 11 raz bol'she. V modeli, kotoruyu my predstavili v
samom nachale, kogda rasstoyanie ot Zemli do Solnca ravno 10 m.,
rasstoyanie do
blizhaishei zvezdy ravno ... 2700 kilometrov !).
Vmesto kompaktnogo i uyutnogo mira, v centre kotorogo nahoditsya
Zemlya, i kotoryi pomeshaetsya vnutri otnositel'no nebol'shoi
nebesnoi sfery, Aristarh narisoval bezdnu. I eta bezdna ispugala
vseh.
, eto bolee 3.5 trillionov
kilometrov (v real'nosti rasstoyanie ot Solnca do blizhaishei zvezdy
eshe primerno v 11 raz bol'she. V modeli, kotoruyu my predstavili v
samom nachale, kogda rasstoyanie ot Zemli do Solnca ravno 10 m.,
rasstoyanie do
blizhaishei zvezdy ravno ... 2700 kilometrov !).
Vmesto kompaktnogo i uyutnogo mira, v centre kotorogo nahoditsya
Zemlya, i kotoryi pomeshaetsya vnutri otnositel'no nebol'shoi
nebesnoi sfery, Aristarh narisoval bezdnu. I eta bezdna ispugala
vseh.
Mezhdu tem, nevozmozhnost' geocentricheskoi sistemy mira, s krugovymi dvizheniyami vseh planet vokrug Zemli, mozhet byt' ustanovlena s pomosh'yu prostoi geometricheskoi zadachi.
Zadacha 2. Na ploskosti dany dve okruzhnosti
s obshim centrom ![]() , po nim ravnomerno dvizhutsya dve tochki:
tochka
, po nim ravnomerno dvizhutsya dve tochki:
tochka ![]() po odnoi okruzhnosti, i tochka
po odnoi okruzhnosti, i tochka ![]() po drugoi. Dokazhite,
chto libo oni dvigayutsya v odnom napravlenii s odinakovoi uglovoi
skorost'yu, libo v nekotoryi moment vremeni ugol
po drugoi. Dokazhite,
chto libo oni dvigayutsya v odnom napravlenii s odinakovoi uglovoi
skorost'yu, libo v nekotoryi moment vremeni ugol
![]() tupoi.
tupoi.
Reshenie. Esli tochki dvizhutsya v odnom
napravlenii s raznymi skorostyami, to cherez nekotoroe vremya luchi
![]() i
i ![]() okazhutsya sonapravlennymi. Dalee ugol
okazhutsya sonapravlennymi. Dalee ugol
![]() nachinaet monotonno vozrastat' do sleduyushego sovpadeniya, t.e., do
nachinaet monotonno vozrastat' do sleduyushego sovpadeniya, t.e., do
![]() . Sledovatel'no, v nekotoryi moment on raven
. Sledovatel'no, v nekotoryi moment on raven ![]() .
Sluchai, kogda tochki dvizhutsya v raznyh napravleniyah rassmatrivaetsya
tak zhe.
.
Sluchai, kogda tochki dvizhutsya v raznyh napravleniyah rassmatrivaetsya
tak zhe.
Teorema 1. Situaciya, pri kotoroi vse planety Solnechnoi sistemy ravnomerno vrashayutsya vokrug Zemli po krugovym orbitam, nevozmozhna.
Dokazatel'stvo. Pust' ![]() - centr Zemli,
- centr Zemli, ![]() - centr Merkuriya, a
- centr Merkuriya, a ![]() - centr Venery. Soglasno mnogoletnim
nablyudeniyam, u Merkuriya i Venery raznye periody obrasheniya, a
ugol
- centr Venery. Soglasno mnogoletnim
nablyudeniyam, u Merkuriya i Venery raznye periody obrasheniya, a
ugol
![]() nikogda ne prevoshodit
nikogda ne prevoshodit ![]() . V silu
rezul'tata zadachi 2, teorema dokazana.
. V silu
rezul'tata zadachi 2, teorema dokazana.
Konechno, drevnie greki neodnokratno vstrechalis' s podobnymi paradoksami. Imenno poetomu, chtoby spasti geocentricheskuyu model' mira, oni zastavili planety dvigat'sya ne po okruzhnostyam, a po cikloidam.
Dokazatel'stvo teoremy 1 ne sovsem chestno, poskol'ku Merkurii i
Venera vrashayutsya ne v odnoi ploskosti, kak v zadache 2, a v raznyh.
Hotya, ploskosti ih orbit pochti sovpadayut: ugol mezhdu nimi - vsego
neskol'ko gradusov. V uprazhnenii 10 my predlagaem Vam ustranit'
etot nedostatok i reshit' analog zadachi 2 dlya tochek, vrashayushihsya v
raznyh ploskostyah. Drugoe vozrazhenie: mozhet byt' ugol ![]() byvaet
tupym, no my etogo ne vidim, poskol'ku na zemle v eto vremya den' ?
Prinimaem i eto. V uprazhnenii 11 nuzhno dokazat', chto dlya
treh vrashayushihsya radiusov
vsegda nastanet moment vremeni, kogda
oni budut obrazovyvat' drug s drugom tupye ugly. Esli na koncah
radiusov - Merkurii, Venera i Solnce, to v etot moment vremeni
Merkurii i Venera budut vidny na nebe, a Solnce - net, to est' na
zemle budet noch'. No dolzhny predupredit': uprazhneniya 10 i 11
znachitel'no slozhnee zadachi 2.
Nakonec, v uprazhnenii 12 my predlagaem Vam, ni mnogo ni malo, vychislit' rasstoyanie ot
Venery do Solnca i ot Merkuriya do Solnca (oni, konechno, vrashayutsya vokrug Solnca, a ne vokrug Zemli).
Ubedites' sami, naskol'ko eto prosto, posle togo, kak my uznali
metod Aristarha.
byvaet
tupym, no my etogo ne vidim, poskol'ku na zemle v eto vremya den' ?
Prinimaem i eto. V uprazhnenii 11 nuzhno dokazat', chto dlya
treh vrashayushihsya radiusov
vsegda nastanet moment vremeni, kogda
oni budut obrazovyvat' drug s drugom tupye ugly. Esli na koncah
radiusov - Merkurii, Venera i Solnce, to v etot moment vremeni
Merkurii i Venera budut vidny na nebe, a Solnce - net, to est' na
zemle budet noch'. No dolzhny predupredit': uprazhneniya 10 i 11
znachitel'no slozhnee zadachi 2.
Nakonec, v uprazhnenii 12 my predlagaem Vam, ni mnogo ni malo, vychislit' rasstoyanie ot
Venery do Solnca i ot Merkuriya do Solnca (oni, konechno, vrashayutsya vokrug Solnca, a ne vokrug Zemli).
Ubedites' sami, naskol'ko eto prosto, posle togo, kak my uznali
metod Aristarha.
Uprazhnenie 10. V prostranstve dany dve okruzhnosti s obshim
centrom ![]() , po nim ravnomerno, s raznymi uglovymi skorostyami,
dvizhutsya dve tochki: tochka
, po nim ravnomerno, s raznymi uglovymi skorostyami,
dvizhutsya dve tochki: tochka ![]() po odnoi okruzhnosti, i tochka
po odnoi okruzhnosti, i tochka ![]() po
drugoi. Dokazhite, chto
v nekotoryi moment
ugol
po
drugoi. Dokazhite, chto
v nekotoryi moment
ugol
![]() tupoi.
tupoi.
Uprazhnenie 11. Na ploskosti dany tri okruzhnosti s obshim
centrom ![]() , po nim ravnomerno, s raznymi uglovymi skorostyami,
dvizhutsya tri tochki. Dokazhite, chto v nekotoryi moment vse tri
ugla mezhdu luchami s vershinoi
, po nim ravnomerno, s raznymi uglovymi skorostyami,
dvizhutsya tri tochki. Dokazhite, chto v nekotoryi moment vse tri
ugla mezhdu luchami s vershinoi ![]() , napravlennymi v dannye tochki,
tupye.
, napravlennymi v dannye tochki,
tupye.
Uprazhnenie 12. Izvestno, chto maksimal'noe uglovoe rasstoyanie
mezhdu Veneroi i Solncem, t.e., maksimal'nyi ugol mezhdu luchami,
napravlennymi s Zemli k centram Venery i Solnca,
ravno ![]() .
Naidite radius orbity Venery. To zhe - dlya Merkuriya, esli
izvestno, chto maksimal'noe uglovoe rasstoyanie mezhdu Merkuriem i
Solncem ravno
.
Naidite radius orbity Venery. To zhe - dlya Merkuriya, esli
izvestno, chto maksimal'noe uglovoe rasstoyanie mezhdu Merkuriem i
Solncem ravno ![]() .
.
Sleduya shag za shagom rassuzhdeniyam Aristarha, my upustili lish' odin
aspekt: kak izmeryalsya uglovoi diametr Solnca ? Sam Aristarh etogo
ne delal, pol'zuyas' izmereniyami drugih astronomov (po-vidimomu, ne
sovsem vernymi). Napomnim, chto radiusy Solnca i Luny on smog
vychislit', ne privlekaya ih uglovye diametry. Posmotrite eshe raz na
shagi 1, 2 i 3: nigde znachenie uglovogo diametra ne ispol'zuetsya !
On nuzhen tol'ko dlya vychisleniya rasstoyanii do Solnca i do Luny.
Popytka opredelit' uglovoi razmer "na glazok" uspeha ne
prinosit. Esli poprosit' neskol'ko chelovek ocenit' uglovoi
diametr Luny, bol'shinstvo nazovut ugol ot 3 do 5 gradusov, chto v
razy bol'she istinnogo znacheniya. Skazyvaetsya obman zreniya:
yarko-belaya Luna na fone temnogo neba kazhetsya massivnoi. Pervym,
kto provel matematicheski strogoe izmerenie uglovogo diametra
Solnca i Luny, byl
Arhimed (287 - 212 do n. e.) On izlozhil svoi metod v knige "Psammit" ("Ischislenie peschinok").
Slozhnost' zadachi on osoznaval:
"Poluchit' tochnoe znachenie etogo ugla - delo nelegkoe, potomu chto
ni glaz, ni ruki, ni pribory, pri pomoshi kotoryh proizvoditsya
otschet, ne obespechivayut dostatochnoi tochnosti." Poetomu Arhimed ne
beretsya vychislit' tochnoe znachenie uglovogo diametra Solnca, on
lish' ocenivaet ego sverhu i snizu. On pomeshaet kruglyi cilindr na
konce dlinnoi lineiki, naprotiv glaza nablyudatelya. Lineika
napravlyaetsya na Solnce, i cilindr pridvigaetsya k glazu do teh por,
poka on ne zaslonit soboi Solnce polnost'yu. Zatem nablyudatel'
uhodit, a na konce lineiki otmechaetsya otrezok ![]() , ravnyi razmeru
chelovecheskogo zrachka (ris. 11).
, ravnyi razmeru
chelovecheskogo zrachka (ris. 11).
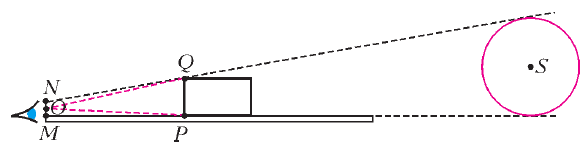 Ris. 11. |
Togda ugol ![]() mezhdu
pryamymi
mezhdu
pryamymi ![]() i
i ![]() men'she uglovogo diametra Solnca, a ugol
men'she uglovogo diametra Solnca, a ugol
![]() - bol'she. My oboznachili cherez
- bol'she. My oboznachili cherez
![]() diametr osnovaniya cilindra, a cherez
diametr osnovaniya cilindra, a cherez ![]() - seredinu
otrezka
- seredinu
otrezka ![]() . Itak,
. Itak,
![]() (dokazhite eto v
uprazhnenii 13). Tak Arhimed nahodit, chto uglovoi diametr Solnca
zaklyuchen v predelah ot
(dokazhite eto v
uprazhnenii 13). Tak Arhimed nahodit, chto uglovoi diametr Solnca
zaklyuchen v predelah ot ![]() do
do ![]() . Neyasnym ostaetsya,
pochemu Arhimed izmeryaet Solnce, a ne Lunu. On byl horosho znakom s
knigoi Aristarha, i znal chto uglovye diametry Solnca i Luny
odinakovy. Lunu zhe izmeryat' gorazdo udobnee: ona ne slepit glaza,
i granicy ee vidny otchetlivee.
. Neyasnym ostaetsya,
pochemu Arhimed izmeryaet Solnce, a ne Lunu. On byl horosho znakom s
knigoi Aristarha, i znal chto uglovye diametry Solnca i Luny
odinakovy. Lunu zhe izmeryat' gorazdo udobnee: ona ne slepit glaza,
i granicy ee vidny otchetlivee.
Nekotorye drevnie astronomy izmeryali uglovoi diametr Solnca,
ishodya iz prodolzhitel'nosti solnechnogo ili lunnogo zatmeniya.
Poprobuite vosstanovit' etot sposob v uprazhnenii 14. A mozhno
sdelat' to zhe, ne dozhidayas' zatmenii, a prosto nablyudaya zakat
Solnca. Vyberem dlya etogo den' vesennego ravnodenstviya 22 marta,
kogda Solnce voshodit tochno na vostoke a zahodit tochno na zapade.
Eto oznachaet, chto tochki voshoda ![]() i zakata
i zakata ![]() diametral'no
protivopolozhny. Dlya zemnogo nablyudatelya Solnce dvizhetsya po
okruzhnosti s diametrom
diametral'no
protivopolozhny. Dlya zemnogo nablyudatelya Solnce dvizhetsya po
okruzhnosti s diametrom ![]() .
.
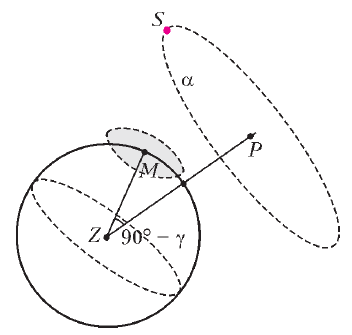 Ris. 12. |
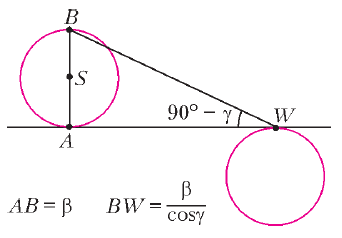 Ris. 13. |
Uprazhnenie 13. Dokazhite, chto ugol ![]() mezhdu pryamymi
mezhdu pryamymi ![]() i
i
![]() (ris. 12.) men'she uglovogo diametra Solnca, a ugol
(ris. 12.) men'she uglovogo diametra Solnca, a ugol
![]() - bol'she.
- bol'she.
Uprazhnenie 14. Predlozhite sposob izmereniya uglovyh razmerov Luny vo vremya lunnogo zatmeniya.
|
Publikacii s klyuchevymi slovami:
astronomiya - istoriya astronomii
Publikacii so slovami: astronomiya - istoriya astronomii | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |