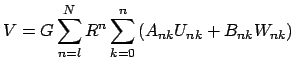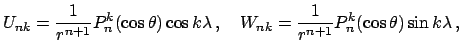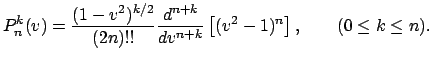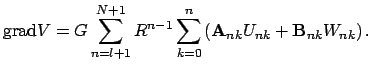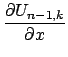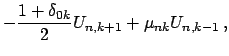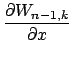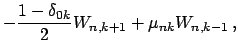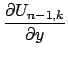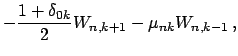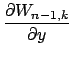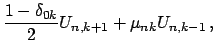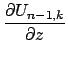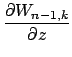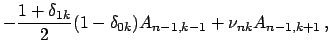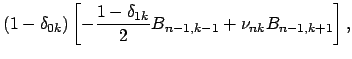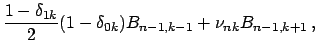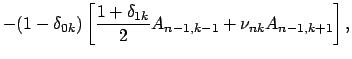<< 1. Vvedenie | Oglavlenie | 3. Srednekvadraticheskaya normalizaciya >>

2. Gravitacionnoe pole nevrashayushegosya tela

Rassmotrim telo , nepodvizhnoe otnositel'no dekartovoi sistemy koordinat  . Ego gravitacionnyi potencial mozhet byt' predstavlen ryadom Laplasa

po sharovym funkciyam

Zdes'  - sfericheskie koordinaty,  - proizvedenie gravitacionnoi postoyannoi na massu ,  - masshtabnyi faktor, i  - bezrazmernye koefficienty Stoksa, postoyannye dlya dannogo tela. V obshem sluchae , , no inogda interes predstavlyaet chast' ryada (1), tak chto my ne priderzhivaemsya etih znachenii , ogranichivaya ih lish' neravenstvami , .

Horosho izvestno, chto gradient sharovoi funkcii sam yavlyaetsya sharovoi funkciei, a ee poryadok povyshaetsya na edinicu [2]:

Ostaetsya tol'ko vyrazit' (takzhe bezrazmernye) komponenty , vektorov cherez . Kratchaishii put' - ispol'zovanie slegka modificirovannyh sootnoshenii [1]

gde

 - simvol Kronekera, , .

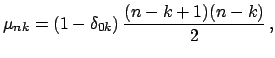
Sravnenie (4) i (5) daet komponenty vektorov kak lineinye kombinacii pri , pri :

pri

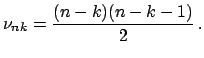
Zamechanie. Obychno schitayut i vne predelov summirovaniya ravnymi nulyu. V chastnosti,

Ispol'zuya (6), my mozhem ne uchityvat' (7), tak kak vse sootvetstvuyushie koefficienty obrashayutsya v nul'.

Stoit zametit' takzhe, chto , a esli nachalo sistemy otscheta pomesheno v centr mass , to

---

<< 1. Vvedenie | Oglavlenie | 3. Srednekvadraticheskaya normalizaciya >>

Publikacii s klyuchevymi slovami: gravitacionnyi potencial - gravimetriya - Nebesnaya mehanika Publikacii so slovami: gravitacionnyi potencial - gravimetriya - Nebesnaya mehanika
Sm. takzhe: Saimon N'yukom (1835 -1909) k 175-letiyu so dnya rozhdeniya. Naum Il'ich Idel'son - 125 let so dnya rozhdeniya Sagitovskie chteniya - 2007 Sagitovskie chteniya - 2006 Metody teorii special'nyh vozmushenii v nebesnoi mehanike Zadacha N tel i problema integriruemosti K 90-letiyu Nikolaya Panteleimonovicha Grushinskogo Vse publikacii na tu zhe temu >>