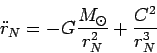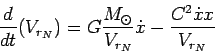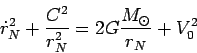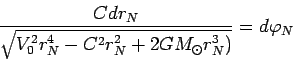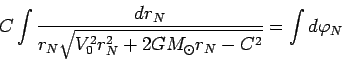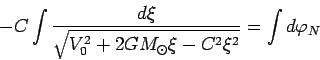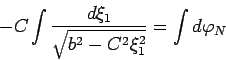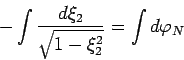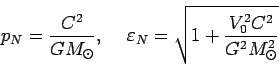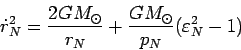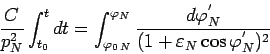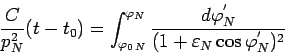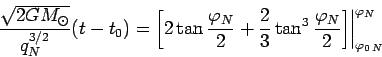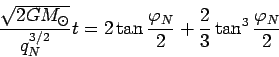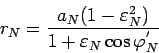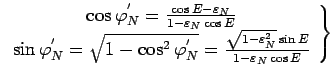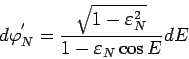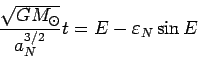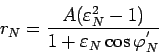<< C. Vychislenie integralov | Oglavlenie | Literatura >>
D. Analiticheskoe reshenie dlya uravnenii dvizheniya yadra komety
V dannom prilozhenii budet rassmotrena zadacha o poiske
analiticheskogo resheniya dlya uravnenii dvizheniya yadra komety (pervaya
para sistemy (50)). Rassmotrim vtoroe
uravnenie sistemy (50)
Proizvedem zamenu peremennyh vida
![]() . Togda
(78) mozhno perepisat' v vide:
. Togda
(78) mozhno perepisat' v vide:
| (79) |
| (80) |
zdes'
Sledovatel'no, pervoe uravnenie sistemy
(50) mozhno predstavit' v vide:
Zdes' uchteno, chto
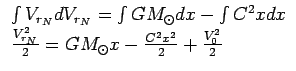 |
Otkuda
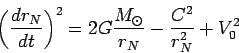 |
(84) |
gde ![]() - postoyannaya integrirovaniya. Uchtem takzhe, chto
- postoyannaya integrirovaniya. Uchtem takzhe, chto
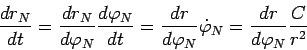
sledovatel'no
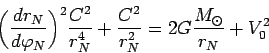
otkuda
Prointegriruem (87)
Proizvedem zamenu peremennyh vida ![]() , togda
, togda
![]() , sledovatel'no (88) mozhno
predstavit' v vide:
, sledovatel'no (88) mozhno
predstavit' v vide:
sledovatel'no, (89) mozhno predstavit' v vide:
proizvedem v (91) zamenu sleduyushego vida
otkuda poluchaem
Vernemsya k ishodnoi peremennoi
gde
gde
uchityvaya opredelenie bol'shoi poluosi orbity yadra
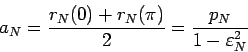 |
(97) |
Podstavlyaya
Situaciya 1: Parabolicheskaya orbita
(
![]() ).
).
Togda posle integrirovaniya v pravoi chasti (101) i
uchityvaya, chto ![]() , gde
, gde ![]() - perigeliinoe rasstoyanie
yadra, budem imet':
- perigeliinoe rasstoyanie
yadra, budem imet':
Reshaya poslednee uravnenie otnositel'no
Situaciya 2: Ellipticheskaya orbita
(
![]() ).
).
V dannom sluchae neposredstvennoe integrirovanie (101)
zatrudnitel'no. V etom sluchae udobno vvesti vspomogatel'nyi ugol
![]() - ekscentricheskuyu anomaliyu i vyrazit'
- ekscentricheskuyu anomaliyu i vyrazit' ![]() ,
, ![]() v
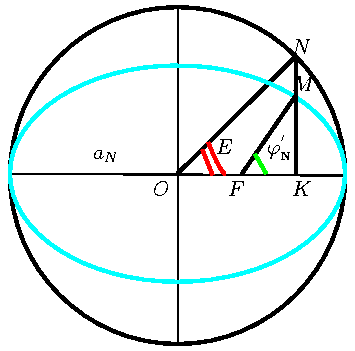
funkcii etogo ugla (smotri ris. 27).
v
funkcii etogo ugla (smotri ris. 27).
Na bol'shoi osi kak na diametre stroim okruzhnost'. Provodim cherez
polozhenie yadra komety (tochka ![]() ) perpendikulyar
) perpendikulyar ![]() k bol'shoi osi
orbity do peresecheniya s okruzhnost'yu. Ugol
k bol'shoi osi
orbity do peresecheniya s okruzhnost'yu. Ugol ![]() i est'
ekscentricheskaya anomaliya
i est'
ekscentricheskaya anomaliya ![]() . Ochevidno, chto
. Ochevidno, chto ![]() ili
ili
ili
Podstavlyaya znachenie
Isklyuchaya iz (105) i (106) peremennuyu
(pered kornem berem znak "+", poskol'ku
Podstavim znachenie
Reshaya poslednee uravnenie otnositel'no peremennoi
Situaciya 3: Giperbolicheskaya
orbita (
![]() ).
).
V sluchae giperbolicheskoi orbity yadra komety
![]() ,
,
![]() , a
, a
Dlya integrirovaniya (101) vvedem vspomogatel'nyi ugol