 Mozhet li nasha Vselennaya byt' konechnoi i topologicheski slozhnoi?
Mozhet li nasha Vselennaya byt' konechnoi i topologicheski slozhnoi?30.12.2003 20:14 | M. E. Prohorov/GAISh, Moskva
V samom nachale 2003 goda poyavilis' pervye dannye nablyudenii reliktovogo fona, vypolnennye na kosmicheskom zonde WMAP (Wilkinson Microwave Anisotropy Probe). Vpervye mnozhestvo kosmologicheskih parametrov byli izmereny s neobychaino vysokoi tochnost'yu. No za neskol'ko mesyacev pervye, samye vazhnye rezul'taty i predskazaniya byli sdelany, vostorgi poutihli i lyubopytstvo uchenyh peremestilos' ot poluchennyh rezul'tatov k problemam, ostavshimsya neob'yasnennymi.
Nablyudeniya
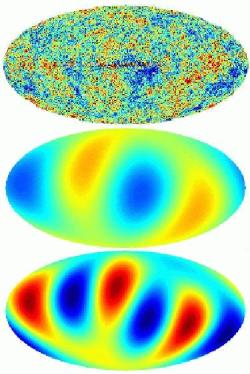
Odna iz etih problem - ochen' nizkie amplitudy dvuh nizshih mul'tipolei (sfericheskih garmonik) reliktovogo fona: kvadrupolya i oktupolya. Eta problema byla izvestna i ranee, to tol'ko v ochen' tochnyh dannyh WMAP ona vstala "vo ves' rost". Na samom dele samoi nizkoi sfericheskoi garmonikoi yavlyaetsya dipol'. On opisyvaet povedenie relikta na uglovyh masshtabah ravnyh 180o : v odnom polusharii nebesnoi sfery temperatura i yarkost' mikrovolnovogo fona okazyvaetsya vyshe, a v drugoi - nizhe. K sozhaleniyu etu garmoniku nevozmozhno otdelit' ot vliyaniya na fon effekta Dopplera, svyazannogo s dvizheniem nablyudatelya. Vtoraya garmonika (kvadrupol') opisyvaet raspredelenie fluktuacii temperatury relikta na uglovyh masshtabah v 90o, a tret'ya garmonika (oktupol'), sootvetstvenno na 60o (sm. Ris. 1). Okazalos', chto nablyudaemaya amplituda kvadrupolya sostavlyaet tol'ko 1/7 ot predskazyvaemogo teoriei urovnya, a amplituda oktupolya - 72% (sm. Ris. 2). Eto otklonenie slishkom veliko i ego trudno ob'yasnit' sluchainymi fluktuaciyami nablyudaemogo mikrovolnovogo kosmicheskogo fona. Nekotorye issledovateli nachali predlagat' vvesti dlya ob'yasneniya etogo otkloneniya "novuyu fiziku" (sm., naprimer, preprint astro-ph/0306597), drugie s nimi ne soglashalis' (astro-ph/0306431). Poka, odnako, nikto ne predlozhil kakoi-libo fizicheskii mehanizm, kotoryi privel by k umen'sheniyu amplitud dvuh nizshih garmonik.
|
| Ris. 1. Karta anizotropii reliktovogo izlucheniya po dannym WMAP (vverhu), ee kvadrupol' (v seredine) i oktupol' (vnizu) iz preprinta astro-ph/0307282. |
|
|
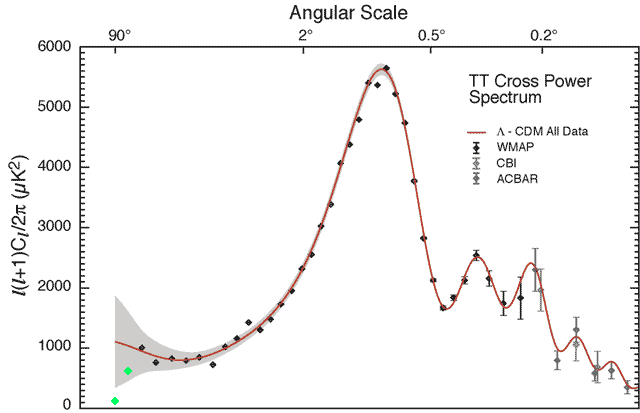
Ris. 2.
Spektr moshnosti uglovyh raspredelenii fluktuacii reliktovogo fonovogo
izlucheniya po dannym WMAP i nekotoryh drugih eksperimentov. Po vertikali
otlozhena amplituda fluktuacii, po gorizontali nomera garmonik (nachinaya
s l=2) ili uglovye masshtaby. Chernye tochki - nablyudatel'nye
dannye, krasnaya liniya - predskazaniya teoreticheskoi modeli dlya ploskoi
Vselennoi, luchshe vsego soglasuyushiesya s nablyudeniyami, seraya polosa -
dopustimaya oshibka teoreticheskih predskazanii. Slishkom nizkie znacheniya
dvuh nizshih garmonik pokazany zelenym cvetom.
Nizkaya amplituda tol'ko odnogo oktupolya (l=3) nedostatochno znachima, no vmeste s ochen' nizkim znacheniem vtoroi garmoniki oni stanovyatsya vazhnym nablyudatel'nym faktom. |
Topologiya
V rabote, Lyumine i dr. opublikovannoi v Nature, takoe reshenie predlozheno, tol'ko ono okazalos' svyazannym ne s fizikoi, a s geometriei, tochnee s topologiei.
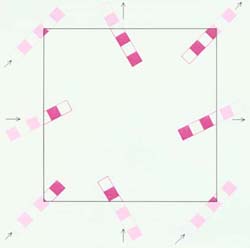
Osnovnaya sut' etogo resheniya zaklyuchaetsya v tom, chto nasha Vselennaya imeet konechnyi ob'em i razmery, kotorye ne mozhet prevyshat' dlina volny samogo krupnomasshtabnogo vozmusheniya v takom Mire. A tot fakt, chto my ne vidim kakih-libo ego granic, ob'yasnyaetsya slozhnoi topologiei. Ideya Vselennoi so slozhnoi topologiei otnyud' ne nova. Fridmanovskie modeli obladayut samymi prostymi iz vozmozhnyh topologii: ploskaya i otkrytaya modeli po topologicheskoi strukture ekvivalentny ploskosti, a zamknutaya model' - sfere (privedeny dvumernye analogii). Sleduyushaya po slozhnosti, posle ploskosti i sfery, figura - tor. Tol'ko ne nado ego predstavlyat' v vide bublika, gorazdo bolee podhodyashee dlya nashih celei predstavlenie - pryamougol'nik u kotorogo skleeny protivopolozhnye storony. Ochen' horoshaya analogiya - ekran nekotoryh igrovyh pristavok: ob'ekt, uhodyashii za pravuyu granicu ekrana, poyavlyaetsya sleva, a ushedshii vniz - sverhu. Pri etom geometriya takogo tora ostaetsya Evklidovoi, t.e. parallel'nye linii ne peresekayutsya, summa uglov treugol'nika ravna 180o i t.d.
|
| Ris. 3. Dvumernyi tor. |
Chtoby poluchit' trehmernyi tor nado poparno skleit' protivopolozhnye storony pryamougol'nogo parallelepipeda (bruska). V etom sluchae poluchitsya beskonechnoe prostranstvo ne imeyushee granic, no s konechnym ob'emom, i v kakuyu by storony my ni smotreli my budem glyadet' v zatylok svoim sobstvennym izobrazheniyam.

|
| Ris. 4. Vid, otkryvayushiisya nablyudatelyu vnutri trehmernogo tora, pohozh na to, chto mozhno uvidet' v komnate, vse steny, pol i potolok kotoroi zerkal'ny; tol'ko izobrazhenie, v otlichie ot obychnogo zerkal'nogo otrazheniya, ne perevernuto. Luch zreniya uhodit, skazhem, skvoz' pravuyu stenu i vozvrashaetsya iz levoi steny; poetomu, glyadya napravo, nablyudatel' vidit komnatu tak, kak budto on smotrit na nee snaruzhi skvoz' prozrachnuyu levuyu stenu (tol'ko pri etom on vidit v komnate svoego dvoinika). Analogichnye kartiny voznikayut pri vzglyade vpered ili vverh. Tak kak luch zreniya pri prodolzhenii neogranichenno pronizyvaet trehmernyi tor, komnata budet vyglyadet' kak prostirayushayasya vo vse storony beskonechnaya pryamougol'naya reshetka. No trehmernyi tor ne beskonechen, poskol'ku vse vidimye obrazy, sostavlyayushie beskonechnuyu pryamougol'nuyu prostranstvennuyu reshetku, - izobrazheniya odnogo i togo zhe predmeta. |
Davaite posmotrim iz kakih figur mozhno stroit' topologicheski slozhnye prostranstva. Usloviya, kotorye na nih nalagayutsya logichny i ponyatny.
- Tela svobodno peresekayut grani ishodnoi figury (gran' - ne stenka): ne dolzhno ostavat'sya ne skleennyh granei.
- V prostranstve net dyr i razryvov: grani skleivayutsya celikom, t.e. imeyut odinakovuyu formu.
- Tela pri peresechenii grani figury ne menyayut svoih razmerov: skleivaemye grani dolzhny byt' odnogo razmera (oni skleivayutsya bez rastyazheniya).
- Tela pri peresechenii rebra ili vershiny ne razryvayutsya:
- sosednie grani figury skleivayutsya s sootvetstvuyushei paroi sosednih granei;
- summa dvugrannyh uglov vokrug rebra dolzhna sostavlyat'
2
 , a trehgrannyh uglov u vershiny - 4
, a trehgrannyh uglov u vershiny - 4 .
.
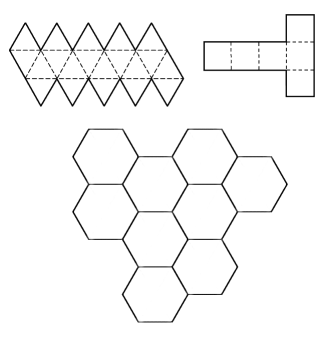
Postroenie prostranstva so slozhnoi topologiei mozhno predstavit' sebe i po drugomu: ne kak skleiku granei odnoi figury, a kak zapolnenie prostranstva beskonechnym chislom kopii nachal'noi figury. (Perechislennye vyshe ogranicheniya dlya takoi procedury oznachayut, chto prostranstvo zapolnyaetsya kopiyami figury bez zazorov i rastyazhenii.) Procedura zapolneniya prostranstva imeet naglyadnuyu analogiyu v dvumerii - zadachu o "parkete" (ili "mozaike") - o moshenii ploskosti bez zazorov odinakovymi geometricheskimi figurami. Ploskost' mozhno bez zazorov pokryt' treugol'nikami, parallelogrammami i central'no-simmetrichnymi shestiugol'nikami.
|
| Ris. 5. Tri vozmozhnyh varianta pokrytiya ploskosti pravil'nymi mnogougol'nikami. |
Dlya zapolneniya trehmernogo prostranstva prigodno takzhe nebol'shoe chislo figur: parallelepipedy i shestigrannye prizmy. Iz pyati pravil'nyh mnogogrannikov (tak nazyvaemyh Platonovyh tel) dlya zapolneniya Evklidova prostranstva goditsya tol'ko kub (sm. Ris. 6). Esli dlya zapolneniya prostranstva ispol'zuyutsya figury (pryamougol'nye parallelepipedy, kuby, pravil'nye shestigrannye prizmy) obladayushie dopolnitel'nymi simmetriyami, to sosednie figury mogut byt' povernuty drug otnositel'no druga (na 90o, 180o ili 60o), chto sootvetstvuet skleike granei figury s sootvetstvuyushim povorotom. Raznye "povoroty" pri skleike sozdayut prostranstva s raznymi topologiyami.
[Bolee podrobno o takih prostranstvah so slozhnoi topologiei mozhno prochitat' v stat'e "Kakuyu formu imeet nasha Vselennaya".]
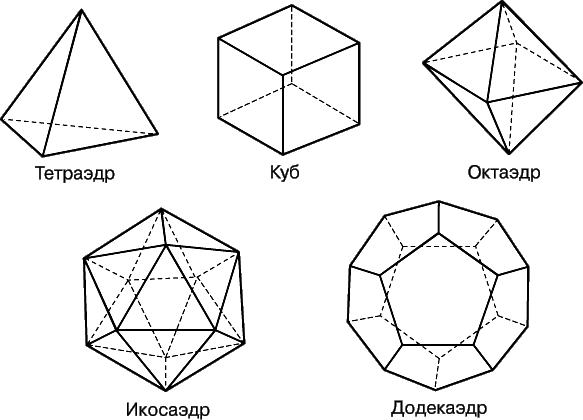
|
| Ris. 6. Pravil'nye mnogogranniki - Platonovy tela. Grani etih figur yavlyayutsya odinakovymi pravil'nymi mnogougol'nikami i v kazhdoi vershine shoditsya odno i to zhe chislo granei. |
Iskrivlennye prostranstva
A vot zapolnit' ploskost' drugimi pravil'nymi mnogougol'nikami ne udastsya. Naprimer u pravil'nogo pyatiugol'nika ugol pri vershine raven 108o. Esli slozhit' tri pyatiugol'nika, to ostanetsya zazor v 36o, a esli chetyre, to oni stanut nakladyvat'sya drug na druga (summa uglov pri vershinah budet ravna 432o, chto prevyshaet 360o). Dlya mnogougol'nikov s chislom storon bol'shim shesti nalozhenie voznikaet uzhe pri popytke slozhit' vmeste tri figury (poskol'ku ugly pravil'nogo n-ugol'nika ravny 180o-360o/n).
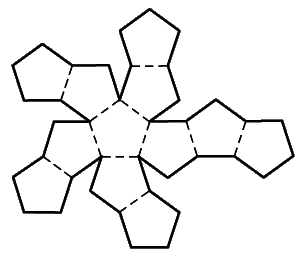
|
| Ris. 7. Popytka pokryt' ploskost' pravil'nymi pyatiugol'nikami. |
Eta kartina ochen' pohozha na to, chto poluchaetsya pri zapolnenii prostranstva dodekaedrami. Eto pravil'nye mnogogranniki, u kotoryh 12 granei, 20 vershin i 30 reber, vse ih grani yavlyayutsya pravil'nymi pyatiugol'nikami, a v kazhdoi vershine shodyatsya tri grani i, sootvetstvenno, tri rebra (sm. Ris. 6). Kak pri popytke slozhit' rebrami tri takih figury, tak i pri sovmeshenii vershin chetyreh mnogogrannikov ostayutsya "sheli".
Chto izmenitsya esli poprobovat' vylozhit' parket ne na ploskoi, a na krivoi poverhnosti? Dlya togo chtoby elementy parketa v raznyh mestah poverhnosti ostavalis' odinakovymi po forme poverhnost' dolzhna obladat' postoyannoi kriviznoi. V dvumernom sluchae postoyannoi otricatel'noi kriviznoi obladayut giperbolicheskie poverhnosti, polozhitel'noi - sfery, a ploskost' yavlyaetsya promezhutochnym sluchaem - poverhnost'yu s postoyannoi nulevoi kriviznoi. Primery etih poverhnostei pokazany na Ris. 8.
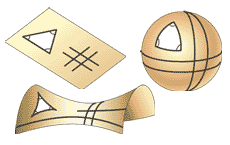
|
| Ris. 8. Dvuhmernye analogi evklidovoi, sfericheskoi i giperbolicheskoi geometrii. V ploskom evklidovom prostranstve parallel'nye pryamye nigde ne peresekayutsya, a summa uglov lyubogo treugol'nika ravna 180o. Na sfericheskoi poverhnosti vse parallel'nye peresekayut drug druga, a summa uglov treugol'nikov vsegda bol'she 180o. Na giperboloide summa uglov treugol'nika men'she 180o, a parallel'nye pryamye rashodyatsya. |
Pryamymi na etih poverhnostyah yavlyayutsya kratchaishie linii, soedinyayushie pary tochek. Na sfere takimi liniyami yavlyayutsya dugi bol'shih krugov (krugov, ploskosti kotoryh prohodyat cherez centr sfery). Sootvetstvenno, figury byvshie na ploskosti treugol'nikami, kvadratami i mnogougol'nikami na sfere prevrashayutsya v sfericheskie treugol'niki i mnogougol'niki. Interesnoi osobennost'yu etih figur yavlyaetsya zavisimost' summy uglov pri ih vershinah ot razmera figury (tochnee ot ee ploshadi). Tak u malen'kogo sfericheskogo treugol'nika summa uglov tol'ko slegka prevyshaet 180o, a u treugol'nika zanimayushego pochti polovinu sfery ona priblizhaetsya k 360o (sm. Ris. 9). Na giperboloide nablyudaetsya protivopolozhnaya kartina: summa uglov mnogougol'nika men'she, chem na ploskosti i ubyvaet s rostom ego razmerov.

|
| Ris. 9. S uvelicheniem razmerov sfericheskogo treugol'nika ego ugly stanovyatsya bolee tupymi, a ih summa uvelichivaetsya. |
Esli vzyat' pravil'nyi pyatiugol'nik na sfere, to pri opredelennyh razmerah ego ugly stanut ravnymi 120o (a ne 108o, kak na ploskosti) i tri takih pyatiugol'nika budut bez zazorov stykovat'sya drug s drugom, esli ih slozhit' vershinami. Bolee togo, dvenadcat' pyatiugol'nikov takogo razmera bez zazorov pokryvayut vsyu sferu. Eta figura vam navernyaka horosho izvestna: nekotoroe vremya nazad tak shili futbol'nye myachi. (Seichas ih chashe vsego sobirayut iz dvuh tipov figur: pyati i shestiugol'nikov.) Po-drugomu, pokazannuyu figuru mozhno predstavit', kak proekciyu reber i granei pravil'nogo dodekaedra na opisannuyu vokrug nego sferu.
 |
 |
| Ris. 10. Futbol'nyi myach - sfera, sobrannaya iz dvenadcati sfericheskih pyatiugol'nikov. | |
Analogichnaya kartina poluchaetsya pri zapolnenii trehmernogo prostranstva "trehmernymi pyatiugol'nikami" - dodekaedrami. Zapolnit' imi Evklidovo prostranstvo "bez shelei" ne udaetsya. No v prostranstve polozhitel'noi krivizny ih ugly (i dvugrannye ugly pri rebrah figury, i telesnye pri vershinah) s uvelicheniem razmerov figury rastut takim obrazom, chto v opredelennyi moment vse zazory ischezayut i 120 sfericheskih dodekaedrov (kazhdyi iz kotoryh sam napominaet futbol'nyi myach) celikom zapolnyayut poverhnost' trehmernoi gipersfery.

|
| Ris. 11. Sto dvadcat' sfericheskih dodekaedrov, polnost'yu zapolnyayushih trehmernuyu gipersferu. |
[Ne menee interesnye rezul'taty poluchayutsya i v giperbolicheskih prostranstvah s otricatel'noi kriviznoi. Bolee podrobno ob etom mozhno prochitat' v stat'e "Matematika trehmernyh mnogoobrazii".]
Vselennaya, postroennaya iz dvenadcatigrannikov, obladaet po krainei mere dvumya preimushestvami po sravneniyu s osnovannoi na kubicheskih torah.
- Dodekaedral'naya struktura zhestkaya, v otlichie ot kubicheskoi, obladayushei shest'yu stepenyami svobody (rastyazheniya po kazhdoi iz treh osei i perekosy).
- Dodekaedral'noe prostranstvo global'no odnorodno, ego geometriya i nablyudaemyi v nem spektr fluktuacii ne zavisyat ot polozheniya nablyudatelya vnutri ishodnogo mnogogrannika.
Periodichnost'
Vo vselennoi (special'no pishu eto slovo s malen'koi bukvy) konechnogo razmera my ne mozhem sozdat' strukturu, masshtab kotoroi prevoshodyat ee razmer. Skleika granei ishodnoi figury ili zapolnenie trehmernogo prostranstva kopiyami ishodnoi oblasti privedut k tomu, chto v vidimoi nami bezgranichnoi Vselennoi razmery struktur i vozmushenii budut ogranicheny tem zhe masshtabom.
A kakie vozmusheniya my uvidim na nebe? Kak oni budut raspredelyat'sya po nebesnoi sfere vo Vselennoi so slozhnoi topologiei?
Esli by Vselennaya ne evolyucionirovala so vremenem, to vse vidimye nam kopii ishodnogo mira polnost'yu sovpadali by drug s drugom. Togda vo Vselennoi postroennoi iz kubov my by videli kartinu, pokazannuyu na Ris. 4. Kazhdyi ob'ekt byl by okruzhen shest'yu svoimi kopiyami, raspolozhennymi vdol' reber kuba. Dipol'naya i kvadrupol'naya sostavlyayushaya v takoi strukture tochno ravny nulyu, a tret'ya garmonika (oktupol') mozhet imet' proizvol'noe vysokuyu amplitudu.
Vo Vselennoi, postroennoi iz dodekaedrov (sm. Ris. 11), kartina byla by neskol'ko drugoi: kazhdyi ob'ekt byl by okruzhen dyuzhinoi svoih kopii, v takoi strukture strogo ravna nulyu amplituda dipolya, sleduyushie dve garmoniki (kvadrupol' i oktupol') podavleny, a amplitudy ostal'nyh opredelyayutsya raspredeleniem struktur v nachal'nom mnogogrannike. Ne pravda li, eta kartina ochen' pohozha na nablyudaemuyu? (sm. Ris. 2.)
Ochen' legko predstavit' i protivopolozhnuyu situaciyu, kogda razmery vidimoi chasti Vselennoi men'she nachal'noi figury. V etom sluchae nablyudaemaya nami kartina ne budet otlichat'sya ot togo, chto my by uvideli v beskonechnoi Vselennoi s prostoi topologiei (eto otlichie mozhet poyavit'sya na bolee pozdnih - v kosmologicheskih masshtabah - vremenah).
Na samom dele vse bolee slozhno. Kogda my nablyudaem drugie galaktiki, to my smotrim ne tol'ko v dal', no i v proshloe. Eto svyazano s konechnost' skorosti sveta. Esli by razmer nashei Vselennoi sostavlyal neskol'ko megaparsek, svet ot kopii nashei Galaktiki dohodil by k nam za neskol'ko millionov let, za eto vremya galaktika izmenyaetsya ne slishkom sil'no, i my smogli by "uznat' sebya" v etih "otrazheniya", a mozhet byt' dazhe popytalis' otyskat' v nih Solnechnuyu sistemu. Esli uvelichit' razmery nachal'nogo mira do soten tysyach svetovyh let podobnoe opoznanie stanovitsya zatrudnitel'nym, a uznat' Mlechnyi Put' za 2-3 milliarda let do nashei ery my by prosto ne smogli. Odnako, vse poiski periodicheskoi struktury s razmerami ot 1000 megaparsek i men'she, kotorye provodilis' poslednie 10-20 let, ne dali polozhitel'nogo rezul'tata. Eto oznachaet, chto esli nasha Vselennaya i imeet ogranichennyi ob'em, to ego razmery ochen' veliki, esli my i vidim samih sebya, to v nastol'ko dalekom proshlom, chto kakoe-libo otozhdestvlenie s sovremennymi ob'ektami stanovitsya prakticheski nevozmozhnym.
Kosmologiya
Kakie predskazaniya daet dodekaedral'naya model' Vselennoi i kak oni sootnosyatsya s nablyudeniyami?
V dannoi modeli prostranstvo dolzhno obladat' polozhitel'noi kriviznoi
(byt' zamknutym), prichem obladat' strogo opredelennym znacheniem
otnosheniya srednei plotnosti k kriticheskoi
![]() (eto znachenie - matematicheskaya
konstanta, kotoruyu mozhno vychislit' s lyubym chislom znakov posle
zapyatoi). I eto znachenie popadaet vnutr' dopustimogo diapazona! Dannye
WMAP dayut
(eto znachenie - matematicheskaya
konstanta, kotoruyu mozhno vychislit' s lyubym chislom znakov posle
zapyatoi). I eto znachenie popadaet vnutr' dopustimogo diapazona! Dannye
WMAP dayut
![]() .
.
[Bolee togo, esli rasschitat' ozhidaemyi spektr vozmushenii ne dlya
ploskoi modeli s ![]() , kak pokazano na Ris. 2, a dlya
, kak pokazano na Ris. 2, a dlya ![]() , to
okazhetsya, chto i oktupol', i dipol' gorazdo luchshe soglasuyutsya s
nablyudeniyami!]
, to
okazhetsya, chto i oktupol', i dipol' gorazdo luchshe soglasuyutsya s
nablyudeniyami!]
Kak ustroena takaya Vselennaya?
Dlya kosmologicheskoi modeli s ![]() radius gorizonta
budet sostavlyat' 38% ot radiusa krivizny Vselennoi (R), a
granicy dodekaedra budut lezhat' v intervale ot 31% R
(centry granei) do 39%R (vershiny) ot ego centra. Ob'em
takogo mnogogrannika budet sostavlyat' 83% ot ob'ema sfery gorizonta.
Otnoshenie razmerov dodekaedra k radiusu krivizny ostaetsya postoyannym,
poskol'ku pri rasshirenii Vselennoi eti velichiny izmenyayutsya
proporcional'no drug drugu. Gorizont Vselennoi vedet sebya po-drugomu.
Ego povedenie zavisit ot zakona rasshireniya, bolee podrobno eto opisano
v stat'e S.Popova (i ssylkah privedennyh v
nei).
radius gorizonta
budet sostavlyat' 38% ot radiusa krivizny Vselennoi (R), a
granicy dodekaedra budut lezhat' v intervale ot 31% R
(centry granei) do 39%R (vershiny) ot ego centra. Ob'em
takogo mnogogrannika budet sostavlyat' 83% ot ob'ema sfery gorizonta.
Otnoshenie razmerov dodekaedra k radiusu krivizny ostaetsya postoyannym,
poskol'ku pri rasshirenii Vselennoi eti velichiny izmenyayutsya
proporcional'no drug drugu. Gorizont Vselennoi vedet sebya po-drugomu.
Ego povedenie zavisit ot zakona rasshireniya, bolee podrobno eto opisano
v stat'e S.Popova (i ssylkah privedennyh v
nei).
Pyatna na nebe
Slozhnaya topologiya nashei Vselennoi budet proyavlyat'sya v nablyudeniya tol'ko v tom sluchae, esli razmery gorizonta prevoshodyat razmery ishodnogo mnogogrannika i v dostupnuyu nam oblast' Vselennoi hotya by chastichno popadayut uchastki ego kopii. Esli zhe ishodnaya figura prevoshodit po razmeram gorizont, no nablyudaemaya kartina ne budet otlichat'sya ot vida beskonechnoi Vselennoi. Shematicheski dannoe utverzhdenie pokazano na Ris. 12.
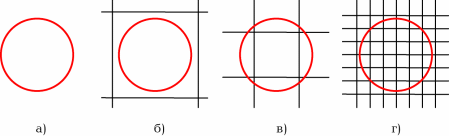
|
|
Ris. 12.
Vozmozhnye sootnosheniya razmerov gorizonta (krasnaya okruzhnost') i
ishodnyh mnogogrannikov: a) beskonechnaya Vselennaya, b) gorizont men'she
ishodnogo mnogogrannika, v) gorizont slegka bol'she ishodnogo mnogogrannika,
g) gorizont ohvatyvaet mnogo kopii ishodnogo mnogogrannika.
V sluchayah a) i b) razlichii nablyudat'sya ne budet. |
Dlya ukazannogo vyshe razmera gorizonta (0.38R) nalichie kopii Vselennoi budet proyavlyat'sya v vide shesti par raspolozhennyh v protivopolozhnyh napravleniyah na nebesnoi sfere krugov diametrom 70o. Oni obrazuyutsya pri peresechenii sfery poslednego rasseyaniya s granyami dodekaedra. Sfera poslednego rasseyaniya (granica rekombinacii) po dannym WMAP raspolozhena na srednem krasnom smeshenii z=1089$\pm$1, t.e. slegka men'she gorizonta. Temperatura reliktovogo izlucheniya v kazhdom iz krugov takoi pary budet odinakovym obrazom otlichat'sya ot srednego ee znacheniya, t.k. registriruemoe ot krugov izluchenie ispuskaetsya oblastyami Vselennoi, zapolnennyh odnim i tem zhe veshestvom (sm. Ris. 13).
|
| Ris. 13. Peresekayushiesya sfery poslednego rasseyaniya dlya osnovnogo mnogogrannika (pokazana sinim cvetom) i dlya nekotoryh ego kopii (zheltym). |
Teoreticheskie aspekty
To, chto nasha Vselennaya mozhet okazat'sya zamknutoi, stavit opredelennye voprosy pered inflyacionnym scenariem, kotoryi segodnya uspeshno ob'yasnyaet bol'shinstvo svoistv okruzhayushei nas Vselennoi. Polnoi yasnosti v etoi probleme (inflyaciya v zamknutoi Vselennoi) poka net, no, kazhetsya, kosmologi gotovy k ee resheniyu.
Zaklyuchenie
Kak podtverdit' ili oprovergnut' model', opisannuyu v dannoi stat'e? Ona predskazyvaet dva sledstviya, kotorye dopuskayut eksperimental'nuyu proverku, prichem v blizhaishee vremya:
- Vselennaya dolzhna byt' zamknutoi s
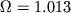 ;
;
- Na nebe dolzhny nablyudat'sya 6 par krugov diametrom 70o (centry kotoryh sootvetstvuyut seredinam granei pravil'nogo dodekaedra) raspredelenie vozmushenii reliktovogo izlucheniya v kotoryh dolzhno poparno korellirovat' drug s drugom.
I, konechno, ostaetsya vozmozhnost', chto dlya privedennyh v nachale dannoi stat'i faktov naidutsya sovsem drugie ob'yasneniya. (Etogo vpolne mozhno ozhidat', tak kak ukazanii v pol'zu imenno takoi topologicheski slozhnoi modeli Vselennoi ochen' malo. Poka imi yavlyayutsya tol'ko nizkie amplitudy dvuh pervyh garmonik spektra moshnosti reliktovogo izlucheniya. Etogo dostatochno, chtoby nachat' obsuzhdat' dannuyu model', no chtoby ubedit' nauchnuyu obshestvennost' v ee "ser'eznosti" nuzhny dopolnitel'nye argumenty.)
|
Publikacii s klyuchevymi slovami:
topologiya Vselennoi - struktura Vselennoi - topologiya
Publikacii so slovami: topologiya Vselennoi - struktura Vselennoi - topologiya | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |