Rambler's Top100Astronet    
  po tekstam   po klyuchevym slovam   v glossarii   po saitam   perevod   po katalogu 		 

Na pervuyu stranicu << A.5 Krivolineinye koordinaty | Oglavlenie | B. Osnovnye terminy >>


A.6 Sfericheskie funkcii

Gravitacionnyi potencial $ U$ vo vseh tochkah, nahodyashihsya na poverhnosti i vne Zemli, udovletvoryaet uravneniyu Laplasa:

$\displaystyle \nabla^2 U=\frac{\partial{^2}U}{\partial{x}^2}+ \frac{\partial{^2}U}{\partial{y}^2}+ \frac{\partial{^2}U}{\partial{y}^2} = 0. $

Operator $ \nabla$ nazyvaetsya "nabla". V sfericheskih koordinatah $ (r,\theta,\lambda)$ uravnenie Laplasa imeet vid:

$\displaystyle \nabla^2 U=\frac{1}{r^2}\frac{\partial{}}{\partial{r}} \left(r^2\frac{\partial{U}}{\partial{r}}\right)+ \frac{1}{r^2\sin\theta} \frac{\partial{}}{\partial{\theta}} \left(\sin\theta\frac{\partial{U}}{\partial{\theta}}\right) + \frac{1}{r^2\sin^2\theta} \frac{\partial{^2} U}{\partial{\lambda}^2}. $

Reshenie uravneniya Laplasa est':

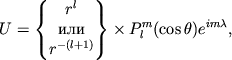
$\displaystyle U= \begin{Bmatrix}r^l \\ \textrm{ili} \\ r^{-(l+1)} \end{Bmatrix}\times P^m_l(\cos\theta)e^{im\lambda}, $

gde $ l,m$ -- celye chisla, prichem $ l\geq 0$ i $ \vert m\vert\leq l$, $ i=\sqrt{-1}$. Funkcii $ P^m_l(\mu)$ nazyvayutsya prisoedinennymi funkciyami Lezhandra stepeni $ l$ i poryadka $ m$. Funkcii $ P^m_l(\mu)$ est' resheniya differencial'nogo uravneniya:

$\displaystyle (1-\mu^2)\frac{d^2P}{d\mu^2} -2\mu\frac{dP}{d\mu} +\left[l(l+1) - \frac{m^2}{1-\mu^2}\right]P=0. $

Pri $ m=0$ poluchaetsya uravnenie Lezhandra. V funkciyah $ P^0_l(\mu)$ verhnii indeks 0 obychno opuskayut.

Opredelim sfericheskie funkcii kak

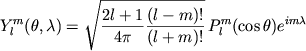
$\displaystyle Y^m_l(\theta,\lambda) =\sqrt{\frac{2l+1}{4\pi}\frac{(l-m)!}{(l+m)!}}\, P^m_l(\cos\theta)e^{im\lambda} $

dlya $ m\geq 0$. Dlya otricatel'nyh $ m$ sfericheskie funkcii opredelyayutsya sleduyushim obrazom: $ Y^m_l\equiv (-1)^mY^{(-m)*}_l$, gde simvol $ ^*$ oznachaet kompleksnoe sopryazhenie.

Polinomy Lezhandra predstavlyayut soboi resheniya uravneniya Laplasa, obladayushie osevoi simmetriei. Ochevidno, esli $ m=0$, to sfericheskie funkcii $ Y^m_l(\theta,\lambda)$ ne zavisyat ot dolgoty, i nazyvayutsya zonal'nymi. Potencial, razlagayushiisya tol'ko po zonal'nym funkciyam, mozhno zapisat' v vide ryada po stepenyam rasstoyaniya $ r$ ot nachala koordinat, koefficientami kotorogo yavlyayutsya polinomy Lezhandra. Oni zavisyat tol'ko ot polyarnogo rasstoyaniya $ \theta$.

Prisoedinennye funkcii Lezhandra yavlyayutsya ortogonal'nymi funkciyami, t.e.

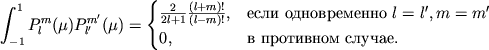
$\displaystyle \int_{-1}^1 P^m_l(\mu)P^{m'}_{l'}(\mu)=\begin{cases} \frac{2}{2l+1}\frac{(l+m)!}{(l-m)!},& \textrm{esli odnovremenno}\ l=l', m=m'\\ 0, & \textrm{v protivnom sluchae}. \end{cases}$

Kazhdaya dvazhdy differenciruemaya deistvitel'naya funkciya $ \Psi(\theta,\lambda)$, takaya chto $ \Psi(\theta,\lambda+2\pi)= \Psi(\theta,\lambda)$ i opredelennaya pri $ 0\leq \theta\leq \pi$ i $ 0\leq \lambda\leq 2\pi$ na poverhnosti sfery, mozhet byt' razlozhena v shodyashiisya ryad

$\displaystyle \Psi(\theta,\lambda)$ $\displaystyle =\sum_{j=0}^{\infty}\left[\frac{1}{2}\alpha_{j0}P_j(\cos\theta) +\sum_{m=0}^j P^m_j(\cos\theta)(\alpha_{jm}\cos m\lambda +\beta_{jm}\sin m\lambda)\right] =$    
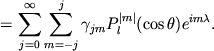$\displaystyle =\sum_{j=0}^{\infty}\sum_{m=-j}^j \gamma_{jm}P^{\vert m\vert}_l(\cos\theta)e^{im\lambda}.$    

Koefficienty razlozheniya nahodyatsya sleduyushim obrazom:

$\displaystyle \alpha_{jm}$ $\displaystyle = \frac{2j+1}{2\pi}\frac{(j-m)!}{(j+m)!} \int_0^{2\pi}d\lambda\, \cos m\lambda\int_0^\pi \Psi(\theta,\lambda) P^m_j(\cos\theta) \sin\theta d\theta,$    
$\displaystyle \beta_{jm}$ $\displaystyle = \frac{2j+1}{2\pi}\frac{(j-m)!}{(j+m)!} \int_0^{2\pi}d\lambda\, \sin m\lambda\int_0^\pi \Psi(\theta,\lambda) P^m_j(\cos\theta) \sin\theta d\theta,$    
$\displaystyle \gamma_{jm}$ $\displaystyle =\gamma^*_{j,-m}=\frac{1}{2}(\alpha_{jm}-i\beta_{jm}) = \frac{2j+1}{4\pi}\frac{(j-m)!}{(j+m)!} \int_0^{2\pi}d\lambda\, e^{im\lambda}\int_0^\pi \Psi(\theta,\lambda) P^m_j(\cos\theta) \sin\theta d\theta,$    

gde $ j=0,1,2,\ldots; m=0,1,2,\ldots, j$.
<< A.5 Krivolineinye koordinaty | Oglavlenie | B. Osnovnye terminy >>

Publikacii s klyuchevymi slovami: astrometriya - sfericheskaya astronomiya - sistemy koordinat - shkaly vremeni
Publikacii so slovami: astrometriya - sfericheskaya astronomiya - sistemy koordinat - shkaly vremeni
Sm. takzhe:
Vse publikacii na tu zhe temu >>

Mneniya chitatelei [13]
Ocenka: 3.5 [golosov: 304]
 
O reitinge
Versiya dlya pechati Raspechatat'

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce

Astronet | Nauchnaya set' | GAISh MGU | Poisk po MGU | O proekte | Avtoram

Kommentarii, voprosy? Pishite: info@astronet.ru ili syuda

Rambler's Top100 Yandeks citirovaniya