A.1 Matrichnaya algebra
Matricei ![]() razmera
razmera ![]() nazyvaetsya tablica skalyarnyh
velichin:
nazyvaetsya tablica skalyarnyh
velichin:
![$\displaystyle A=
\begin{pmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \cdots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn}
\end{pmatrix} \equiv [a_{ij}],
$](https://images.astronet.ru/pubd/2003/06/11/0001190894/tex/formula931.gif)
Dlya matric opredeleny sleduyushie operacii:
- Matricy
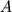 i
i 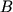 razmera
razmera 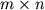 ravny
ravny 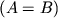 , esli
dlya vseh
, esli
dlya vseh 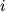 i
i 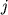 ravny ih elementy:
ravny ih elementy:
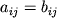 .
.
- Summa matric
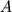 i
i 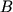 razmera
razmera 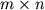 est' matrica
est' matrica
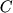 razmera
razmera 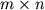 :
:
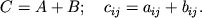
- Proizvedenie matricy
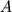 razmera
razmera 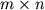 na skalyar
na skalyar 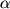 est' matrica
est' matrica 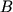 razmera
razmera 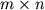 :
:
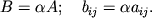
- Proizvedenie matricy
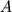 razmera
razmera 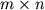 na matricu
na matricu 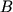 razmera
razmera 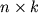 est' matrica
est' matrica 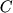 razmera
razmera 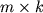 :
:
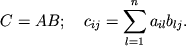
Matrica ![]() , transponirovannaya po otnosheniyu k matrice
, transponirovannaya po otnosheniyu k matrice ![]() razmera
razmera ![]() , est' matrica
, est' matrica
![]() razmera
razmera
![]() . Spravedlivy sleduyushie sootnosheniya:
. Spravedlivy sleduyushie sootnosheniya:
Matrica ![]() razmera
razmera ![]() nazyvaetsya kvadratnoi matricei
poryadka
nazyvaetsya kvadratnoi matricei
poryadka ![]() .
.
Kvadratnaya matrica ![]() nazyvaetsya diagonal'noi, esli vse
nediagonal'nye elementy
nazyvaetsya diagonal'noi, esli vse
nediagonal'nye elementy ![]()
![]() ravny nulyu.
ravny nulyu.
Diagonal'naya matrica ![]() razmera
razmera ![]() nazyvaetsya
edinichnoi:
nazyvaetsya
edinichnoi: ![]() , esli vse diagonal'nye elementy ravny edinice:
, esli vse diagonal'nye elementy ravny edinice:
![]() ,
, ![]() pri
pri ![]() . Esli
. Esli ![]() -- edinichnaya
matrica razmera
-- edinichnaya
matrica razmera ![]() , to dlya lyuboi matricy
, to dlya lyuboi matricy ![]() razmera
razmera
![]() spravedlivy ravenstva
spravedlivy ravenstva ![]() .
.
Kvadratnaya matrica ![]() nazyvaetsya simmetricheskoi, esli
nazyvaetsya simmetricheskoi, esli ![]() ,
t.e. esli
,
t.e. esli
![]() .
.
Kvadratnaya matrica ![]() nazyvaetsya nevyrozhdennoi, esli ona imeet
edinstvennuyu obratnuyu matricu
nazyvaetsya nevyrozhdennoi, esli ona imeet
edinstvennuyu obratnuyu matricu ![]() , opredelyaemuyu usloviem:
, opredelyaemuyu usloviem:
![]() .
.
Kvadratnaya matrica ![]() nazyvaetsya ortogonal'noi, esli
nazyvaetsya ortogonal'noi, esli
![]() , t.e. esli
, t.e. esli
![]() .
.
Esli kvadratnye matricy ![]() i
i ![]() odnogo poryadka nevyrozhdeny,
skalyar
odnogo poryadka nevyrozhdeny,
skalyar
![]() , to
, to
Kvadratnaya matrica ne vyrozhdena togda i tol'ko togda, kogda ee stroki (stolbcy) lineino nezavisimy.
<< A. Osnovnye matematicheskie opredeleniya | Oglavlenie | A.2 Lineinaya algebra >>
|
Publikacii s klyuchevymi slovami:
astrometriya - sfericheskaya astronomiya - sistemy koordinat - shkaly vremeni
Publikacii so slovami: astrometriya - sfericheskaya astronomiya - sistemy koordinat - shkaly vremeni | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |