Astronet > Geofizicheskie metody issledovaniya zemnoi kory. Chast' 1

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Geofizicheskie metody issledovaniya zemnoi kory

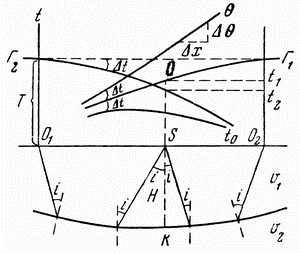3. Obratnaya zadacha metoda prelomlennyh voln. Obratnaya zadacha metoda prelomlennyh voln (MPV) nad naklonnoi granicei dvuh sred svoditsya k opredeleniyu skorostei v verhnem ( $V_{1}$ ) i nizhnem ( $V_{2 }= V_{g}$ ) sloyah i geometricheskih parametrov razreza (N, \varphi). Ee reshayut razlichnymi sposobami, osnovannymi na analize uravneniya godografa (4.8) - (4.10). Kak pokazyvaet praktika interpretacii MPV, naibolee nadezhno reshit' obratnuyu zadachu mozhno, imeya vstrechnye godografy (G₁ i G₂), kotorye poluchayutsya iz dvuh tochek vzryva O₁ i O₂, nahodyashihsya na koncah izuchaemogo profilya (ris. 4.8).

Ris. 4.8. Opredelenie granichnoi skorosti s pomosh'yu raznostnogo godografa i postroenie prelomlyayushei granicy sposobom $t_{0}$

A. Opredelenie granichnoi skorosti po raznostnomu godografu. Imeya dva vstrechnyh godografa, mozhno postroit' raznostnyi godograf: $\theta (x) = t_{1}(x) - t_{2}(x) + T$ , gde $t_{1}(x)$ i $t_{2}(x)$ - vremya prihoda golovnoi prelomlennoi volny v tochku h po pervomu i vtoromu (vstrechnomu) godografu, $T$ - vremya vo vzaimnyh tochkah, t.e. vremya prihoda volny iz O₁ v O₂ ili iz O₂ v O₁ (sm. ris. 4.8). Legko videt', chto put' golovnoi volny iz punkta vzryva O₁ v tochku O₂ i, naoborot, iz punkta vzryva O₂ v tochku O₁ odinakov, a znachit, vremya vo vzaimnyh tochkah po vstrechnym godografam odinakovo i postoyanno dlya dannogo intervala O₁O₂ (ris. 4.8).

Vzyav proizvodnuyu ot uravneniya raznostnogo godografa, poluchim $d\theta / dx = = dt_{1 }/dx - dt_{2 }/ dx$ , gde $d\theta /dx = \Delta\theta /\Delta x$ - uglovoi koefficient raznostnogo godografa, ravnyi obratnoi skorosti, t.e.

$\frac{{dt}_{1} }{dx} = \frac{\Delta {t}_{1} }{\Delta x} = \frac{1}{{V}_{kp}} \mbox{i}\; \frac{{dt}_{2} }{dx} = \frac{\Delta {t}_{2} }{\Delta x} = - \frac{1}{V_{kv}}.$

Otsyuda

$\frac{\Delta\theta }{\Delta x} = \frac{1}{{V}_{kp}} + \frac{1}{{V}_{kv}} = \frac{\sin (i+\varphi ) + \sin (i-\varphi )}{V_1} = \frac{2\cos \varphi }{V_g}$

Takim obrazom, granichnaya skorost' mozhet byt' opredelena po naklonu raznostnogo godografa ${V}_{g} = 2\cos\varphi \cdot \Delta x / \Delta\theta$ . Pri uglah naklona, men'shih 10 - 15 $^\circ$ , $V_{g} \approx 2\Delta x/\Delta\theta$ .

B. Opredelenie skorosti v perekryvayushem sloe. Skorost' uprugih voln v perekryvayushem sloe (tolshe) $V_{1}(V_{sr})$ mozhet byt' ocenena po tochkam peresecheniya godografov pryamoi i golovnyh prelomlennyh voln: ${V}_{1} \approx {V}_{sr} \approx x_{tp }/t_{tp}$ , gde $h_{tp}$ i $t_{tp}$ - koordinaty tochek peresecheniya.

Odnako bolee tochno $V_{sr} \approx V_{ef}$ poluchaetsya po dannym metoda otrazhennyh voln (10.3.2).

V. Postroenie prelomlyayushei granicy sposobom nulevogo vremeni. Odnim iz prostyh i tochnyh sposobov opredeleniya $H, \varphi$ i postroeniya prelomlyayushei granicy yavlyaetsya sposob nulevogo vremeni ( $t_{0}$ ).

Dlya lyuboi tochki $S$ , gde imeyutsya dva vstrechnyh godografa (sm. ris. 4.8), mozhno naiti nekotoruyu funkciyu $t_{0} = t_{1} + t_{2} - T$ , kotoraya ravna vremeni na punkte vzryva $t_{0} = 2 H \cos i / V_{1}$ . V samom dele, $t_{1} = t_{O_{1} AC} + t_{CS},\; t_{2} = t_{O_{2} BD} + t_{DS}, T = t_{O_{1} AC} + t_{O_{2} BD} + t_{CD}$ . Otsyuda, schitaya granicu na uchastke SD ploskoi i opustiv iz S perpendikulyar na SD, poluchim

${t}_{1} + {t}_{2} - T = {t}_{CS} +{t}_{DS} - {t}_{CD} = 2{t}_{CS} - 2{t}_{CK} = \frac{2CS}{{V}_{1}} - \frac{2CK}{{V}_{g}}.$

Iz treugol'nika CSK: $CS = H / \cos i,\; CK = H \rm{tg}\; i$ . Uchityvaya, chto $\sin i = V_{1 }/V_{g}$ , poluchim:

${t}_{o} = {t}_{1} + {t}_{2} - T = \frac{2H}{\cos i{V}_{1} } - \frac{2H\rm{tg}\; i}{{V}_{1}} = \frac{2H}{{V}_{1}} \left( \frac{1}{\cos i} - \frac{\sin^2 i}{\cos i}\right) = \frac{2H\cos i}{V_1}.$

(4.12)

Sledovatel'no, dlya lyuboi tochki profilya, gde imeyutsya vstrechnye godografy, mozhno naiti fiktivnoe vremya $t_{0} = t_{1} + t_{2} - T$ , a zatem i rasschitat'

$H = \frac{t_o V_1}{2\cos i} = \frac{t_o}{2\sqrt{\frac{1}{v_1^2} - \frac{1}{v_g^2}}}.$

(4.13)

Prakticheski primenenie sposoba $t_{0}$ svoditsya k sleduyushemu. Dlya lyuboi tochki h opredelyaetsya velichina $\Delta t = T - t_{2}$ . Ot znacheniya $t_{1}$ po pervomu godografu izmeritelem otkladyvaetsya $\Delta t$ vverh (poluchaem tochku raznostnogo godografa $\theta = t_{1} + \Delta t = t_{1} - t_{2} + T$ ) i vniz (poluchaem $t_{0} = t_{1} - \Delta t = t_{1} + t_{2} - T$ ). Sdelav podobnye postroeniya v neskol'kih (3 - 5) tochkah osi h i soediniv tochki $\theta$ i $t_{0}$ , poluchaem raznostnyi godograf $\theta (h)$ i liniyu $t_{0 }(x)$ . Po naklonu raznostnogo godografa nahoditsya granichnaya skorost' $V_{g} \approx 2 \Delta h / \Delta\theta$ (pri $\varphi \lt 15^\circ$ ). Esli ugol $\varphi \gt 15^\circ$ , to ee mozhno opredelit' po formule, privedennoi vyshe ( $V_{g} = 2 \cos\varphi \Delta x / \Delta\theta$ ). Znaya $t_{0}$ v kazhdoi tochke, po formule (4.13) mozhno rasschitat' eho-glubinu $N$ .

Provedya iz neskol'kih tochek h dugi radiusami $N$ i soediniv ih plavnoi kasatel'noi, poluchim iskomuyu prelomlyayushuyu krivolineinuyu granicu razdela. Dlya krivolineinoi granicy ne imeet smysla govorit' ob ugle naklona $\varphi$ , poskol'ku on raznyi v raznyh tochkah prelomlyayushei granicy.

Privedennye pryamye i obratnye zadachi MOV i MPV dlya dvuhsloinogo razreza yavlyayutsya osnovnymi zadachami seismorazvedki, poskol'ku, zameniv verhnii sloi ( $V_{1}, H, \varphi$ ) tolshei ( $V_{sr}, H, \varphi$ ), poluchaem prakticheski odni i te zhe godografy. Reshenie kinematicheskih pryamyh i obratnyh zadach dlya otrazhennyh, prelomlennyh, refragirovannyh, difragirovannyh voln sloistyh tolsh (odnomernye zadachi - 1D), sred s vytyanutymi kontaktami (dvuhmernye zadachi - 2D) i dlya vklyuchenii ob'ektov (trehmernye zadachi - 3D) v analiticheskom vide svyazano s bol'shimi matematicheskimi slozhnostyami.

10.3.4. Principy resheniya obratnoi zadachi metoda refragirovannyh voln.

Reshenie obratnoi zadachi metoda refragirovannyh voln (MRV) slozhnee, chem prelomlennyh. Oni svodyatsya k postroeniyu skorostnyh razrezov ili polei skorostei, na kotoryh dlya kazhdoi tochki razreza izvestna skorost'. Dlya raznyh zakonov izmeneniya skorostei s glubinoi razrabotany razlichnye priemy postroeniya skorostnyh razrezov po godografam refragirovannyh voln. Rassmotrim odin iz prostyh dlya sredy s vertikal'nym gradientom skorosti. Ona prinimaetsya za sloisto-odnorodnuyu, sostoyashuyu iz beskonechno tonkih gorizontal'nyh sloev, v kazhdom iz kotoryh skorosti postoyanny, a na granicah vozrastayut skachkom, no takim obrazom, chto chem glubzhe sloi, tem vyshe skorost' v nem (sm. ris. 4.1). Dlya takih razrezov mozhno vospol'zovat'sya resheniem obratnoi zadachi MPV nad mnogosloinoi sredoi. Na godografe refragirovannoi volny vybiraetsya neskol'ko (do 5) tochek ( $t_{1}, t_{2}, \ldots$ ) i v kazhdoi iz nih provoditsya kasatel'naya (ris. 4.9). Po peresecheniyu kasatel'nyh s os'yu vremen opredelyayutsya $t_{01}, t_{02}, \ldots$ , a po ih naklonu - kazhushiesya skorosti $V_{K1} = \Delta h_{1 }/ \Delta t_{1}, V_{K2} = \Delta x_{2 }/ \Delta t_{2}, \ldots$

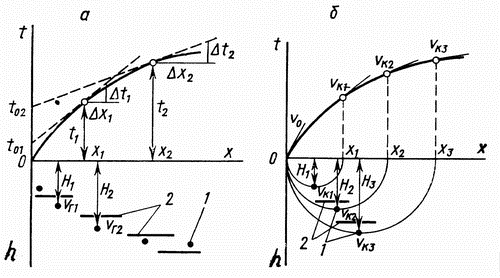Ris. 4.9. Godografy refragirovannyh voln (a) i (b), a takzhe postroennye s ih pomosh'yu skorostnye razrezy: 1 - tochki razreza, dlya kotoryh opredelena skorost'; 2 - izolinii skorostei

V 10.3.3 polucheno vyrazhenie dlya kazhusheisya skorosti golovnoi prelomlennoi volny, kotoraya v sluchae gorizontal'noi prelomlyayushei granicy ( $\varphi = 0$ ) ravna $V_{ K} = V_{sr }/\sin i = {V}_{g}$ (zdes' primenena formula $\sin i = { V}_{sr }/{V}_{g}$ ). Poetomu mozhno zapisat' ${V}_{k1 }= {V}_{g1}, {V}_{k2 }= {V}_{g2}, \ldots$

Za srednyuyu skorost' $V_{sr1}, V_{sr2}, \ldots$ v pokryvayushei srede nad sootvetstvuyushimi prelomlyayushimi ploshadkami s $V_{G1}, {V}_{G2}, \ldots$ prinimaetsya poluchennoe empiricheskim putem vyrazhenie ${V}_{cpi} = 0,5[{x}_{i} /{t}_{i} + \sqrt{({x}_{i} /{t}_{i} )\cdot {v}_{ki} } ]$ , gde $x_{i }/ t_{i}$ - skorost' v pokryvayushei tolshe, esli schitat' ee negradientnoi; $i = 1, 2, \ldots$ Po izvestnym $t_{0}, {V}_{G}$ i ${V}_{cp}$ mozhno opredelit' glubinu zaleganiya prelomlyayushih ploshadok:

$H = {t}_{o} /2\sqrt{1/{v}_{cp}^{2} - 1/{v}_{g}^{2} }.$

Dlya prakticheskogo postroeniya skorostnogo razreza dannym metodom ot tochek profilya, raspolozhennyh v seredine mezhdu punktom vozbuzhdeniya i raschetnymi tochkami $h_{1}, h_{2}, \ldots$ , vniz otkladyvayutsya glubiny $N_{1}, N_{2}, \ldots$ i u nih zapisyvayutsya granichnye skorosti ${V}_{G1}, {V}_{G2}, \ldots$ Esli provesti izolinii, to poluchim skorostnoi razrez. Postroenie skorostnyh razrezov opisannymi vyshe sposobami obychno vypolnyaetsya na komp'yuterah.

Nazad| Vpered

Publikacii s klyuchevymi slovami: geofizika - Zemlya - zemnaya kora Publikacii so slovami: geofizika - Zemlya - zemnaya kora
Sm. takzhe: Vsya voda na planete Zemlya Dva mira, dve analemmy Dva mira, odno Solnce Zamerzshie puzyri metana v ozere Baikal Zemlya iz mezhplanetnogo prostranstva Zahod Zemli s "Oriona" Protivosumerechnye luchi i festival' planet Vse publikacii na tu zhe temu >>

Mneniya chitatelei [5]

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce