Avtomodel'nost'
1.08.2001 0:00 | "Fizicheskaya Enciklopediya"/Phys.Web.Ru
Avtomodel'nost' - osobaya simmetriya fizicheskoi sistemy,
sostoyashaya v tom, chto izmenenie masshtabov
nezavisimyh peremennyh mozhet byt' skompensirovano preobrazovaniem podobiya drugih
dinamicheskih peremennyh. Avtomodel'nost' privodit
k effektivnomu
sokrasheniyu
chisla nezavisimyh peremennyh. Naprimer, esli sostoyanie sistemy harakterizuetsya
funkciei ![]() , gde h - koordinata,
t - vremya, to uslovie invariantnosti
otnositel'no izmeneniya masshtabov
, gde h - koordinata,
t - vremya, to uslovie invariantnosti
otnositel'no izmeneniya masshtabov ![]() ,
, ![]() i preobrazovaniya podobiya takovo:
i preobrazovaniya podobiya takovo:
![]() .
.
gde ![]() - chisla. Vybor
- chisla. Vybor ![]() , gde m - kriterii
podobiya (parametr), pridaet pervonachal'noi
funkcii
avtomodel'nyi vid
, gde m - kriterii
podobiya (parametr), pridaet pervonachal'noi
funkcii
avtomodel'nyi vid
![]()
T. o., funkciya u pri postoyannom m zavisit
tol'ko ot kombinacii ![]() . Avtomodel'nost' vozmozhna,
esli nabor parametrov, opredelyayushih sostoyanie
sistemy, ne soderzhit harakternyh masshtabov nezavisimyh peremennyh. Poskol'ku
v bol'shinstve zadach forma preobrazovaniya podobiya
zaranee neizvestna,
avtomodel'nuyu
podstanovku nado v kazhdom sluchae nahodit' otdel'no. Dlya etogo imeyutsya 3 sposoba:
. Avtomodel'nost' vozmozhna,
esli nabor parametrov, opredelyayushih sostoyanie
sistemy, ne soderzhit harakternyh masshtabov nezavisimyh peremennyh. Poskol'ku
v bol'shinstve zadach forma preobrazovaniya podobiya
zaranee neizvestna,
avtomodel'nuyu
podstanovku nado v kazhdom sluchae nahodit' otdel'no. Dlya etogo imeyutsya 3 sposoba:
- Analiz razmernostei. Sostoyanie sistemy
harakterizuetsya naborom razmernyh parametrov i funkcii, zavisyashih ot koordinat h,
u, z i vremeni
t.
Esli odin iz bezrazmernyh kriteriev podobiya imeet vid m =
H0/b
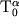 ,
gde b - parametr, imeyushii razmernost' [b]
=
,
gde b - parametr, imeyushii razmernost' [b]
= 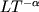 , X0,
T0 - harakternye dlina i promezhutok vremeni,
L, T - edinicy dliny
i vremeni sootvetstvenno, to v kachestve
avtomodel'nyh peremennyh mozhno vybrat' bezrazmernye kombinacii x/b
, X0,
T0 - harakternye dlina i promezhutok vremeni,
L, T - edinicy dliny
i vremeni sootvetstvenno, to v kachestve
avtomodel'nyh peremennyh mozhno vybrat' bezrazmernye kombinacii x/b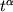 ,
y/b
,
y/b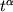 ,
z/b
,
z/b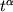 . V tom sluchae, kogda
imeetsya ne bolee dvuh opredelyayushih parametrov s nezavisimymi razmernostyami, otlichnymi
ot dliny i vremeni, perehod
k
avtomodel'nym
peremennym prevrashaet uravnenie s chastnymi proizvodnymi
v obyknovennoe differencial'noe uravnenie.
. V tom sluchae, kogda
imeetsya ne bolee dvuh opredelyayushih parametrov s nezavisimymi razmernostyami, otlichnymi
ot dliny i vremeni, perehod
k
avtomodel'nym
peremennym prevrashaet uravnenie s chastnymi proizvodnymi
v obyknovennoe differencial'noe uravnenie.
- Neposredstvennyi podbor. Formal'no vvoditsya avtomodel'naya zamena peremennyh
u=rf(x/
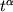 ) ili,
v bolee obshem vide, u=
) ili,
v bolee obshem vide, u=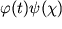 ,
,
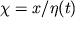 . Uravneniya, nachal'nye i granichnye usloviya
dolzhny imet' strukturu, dopuskayushuyu takuyu zamenu. Reshenie sushestvuet ne dlya lyubyh
znachenii
. Uravneniya, nachal'nye i granichnye usloviya
dolzhny imet' strukturu, dopuskayushuyu takuyu zamenu. Reshenie sushestvuet ne dlya lyubyh
znachenii 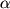 ,
,
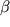 i ne dlya lyubyh funkcii
i ne dlya lyubyh funkcii 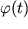 i
i 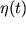 . Dlya polucheniya podhodyashih znachenii neobhodimo
reshit' nelineinuyu zadachu
na sobstvennye znacheniya.
. Dlya polucheniya podhodyashih znachenii neobhodimo
reshit' nelineinuyu zadachu
na sobstvennye znacheniya.
Issledovanie gruppovyh svoistv uravnenii. Rassmotrim sistemu differencial'nyh uravnenii s chastnymi proizvodnymi 1-go poryadka fj (hi, uk, pik) = 0, gde hi - nezavisimye peremennye, uk - iskomye funkcii, rik =
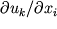 . Vsevozmozhnye zameny peremennyh
hi, uk,
dopuskaemye sistemoi, obrazuyut gruppu
Li. Avtomodel'nye zameny yavlyayutsya ee odnoparametricheskoi
podgruppoi rastyazhenii. V nekotoryh sluchayah naiti takie zameny pozvolyaet
sleduyushaya procedura.
. Vsevozmozhnye zameny peremennyh
hi, uk,
dopuskaemye sistemoi, obrazuyut gruppu
Li. Avtomodel'nye zameny yavlyayutsya ee odnoparametricheskoi
podgruppoi rastyazhenii. V nekotoryh sluchayah naiti takie zameny pozvolyaet
sleduyushaya procedura.V prostranstve peremennyh hi, uk gruppa Li zadaetsya svoimi generatorami, imeyushimi obshii vid H =
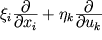 , gde
, gde
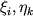 - nekotorye funkcii peremennyh h, i; po povtoryayushimsya indeksam
proizvoditsya summirovanie. V prostranstve peremennyh hi,
uk,
pik
gruppa Li zadaetsya generatorami
- nekotorye funkcii peremennyh h, i; po povtoryayushimsya indeksam
proizvoditsya summirovanie. V prostranstve peremennyh hi,
uk,
pik
gruppa Li zadaetsya generatorami 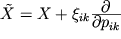 gde
gde 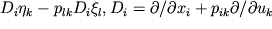 . Sistema uravnenii
fj = 0 opredelyaet giperpoverhnost'
v prostranstve peremennyhhi,
uk, pik,
kotoraya yavlyaetsya invariantom gruppy pri uslovii
Hfj = 0, kogda fj
=
0; eti usloviya sluzhat dlya opredeleniya funkcii \xi_i (h, i)
i \eta_k (h, u). Kombinacii peremennyh,
dayushie iskomuyu zamenu, yavlyayutsya pervymi
integralami uravneniya . Naprimer, dlya
dvuh nezavisimyh peremennyh
h, t i odnoi iskomoi funkcii u
operator rastyazhenii imeet vid X =
. Sistema uravnenii
fj = 0 opredelyaet giperpoverhnost'
v prostranstve peremennyhhi,
uk, pik,
kotoraya yavlyaetsya invariantom gruppy pri uslovii
Hfj = 0, kogda fj
=
0; eti usloviya sluzhat dlya opredeleniya funkcii \xi_i (h, i)
i \eta_k (h, u). Kombinacii peremennyh,
dayushie iskomuyu zamenu, yavlyayutsya pervymi
integralami uravneniya . Naprimer, dlya
dvuh nezavisimyh peremennyh
h, t i odnoi iskomoi funkcii u
operator rastyazhenii imeet vid X = 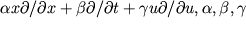 - chisla. Nabor pervyh integralov
uravneniya
- chisla. Nabor pervyh integralov
uravneniya 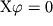 takov:
takov: 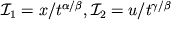 , poetomu avtomodel'noe reshenie
uravnenii, dopuskayushih gruppu rastyazhenii, budet
imet' vid
, poetomu avtomodel'noe reshenie
uravnenii, dopuskayushih gruppu rastyazhenii, budet
imet' vid 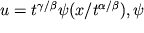 - novaya iskomaya funkciya.
- novaya iskomaya funkciya.Rassmotrim, naprimer, uravnenie Kortevega-de Frisa
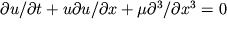 ,
gde
,
gde 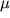 - postoyannyi parametr; ono invariantno otnositel'no
preobrazovaniya
- postoyannyi parametr; ono invariantno otnositel'no
preobrazovaniya 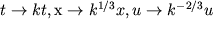 . Generator
. Generator
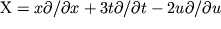 - operator
rastyazhenii, i avtomodel'noe reshenie imeet vid
- operator
rastyazhenii, i avtomodel'noe reshenie imeet vid
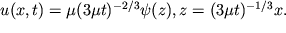
Podstavlyaya eto reshenie v ishodnoe uravnenie, poluchaem obyknovennoe differencial'noe uravnenie dlya funkcii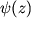 :
:
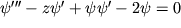
Odnoparametricheskaya gruppa rastyazhenii abeleva. Esli sistema dopuskaet resheniya, postroennye na drugih odnoparametricheskih abelevyh podgruppah, to podhodyashei zamenoi etim resheniyam mozhno pridat' avtomodel'nyi vid, chto yavlyaetsya sledstviem podobiya etih grupp. V chastnosti, avtomodel'nye dvizheniya tesno svyazany s nelineinymi begushimi volnami, t. e. resheniyami vida
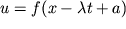 , dlya kotoryh mesto preobrazovaniya podobiya zanimaet preobrazovanie
sdviga.
Zamena
, dlya kotoryh mesto preobrazovaniya podobiya zanimaet preobrazovanie
sdviga.
Zamena
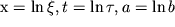 perevodit volnovoe
reshenie f v avtomodel'noe:
perevodit volnovoe
reshenie f v avtomodel'noe:
![$f[\ln{(\xi/bt^\lambda)}] =F(\xi/bt^\lambda).$](https://images.astronet.ru/pubd/2001/10/30/0001172228/tex/formula35.gif)
Avtomodel'nost', otrazhayushaya vnutrennyuyu simmetriyu, prisusha mnogim yavleniyam i ispol'zuetsya pri reshenii razlichnyh fizicheskih zadach, osobenno v mehanike sploshnyh sred (sm. Avtomodel'noe techenie).
Metod renormalizacionnoi gruppy v kvantovoi teorii polya, po sushestvu, takzhe osnovan na ispol'zovanii avtomodel'nogo preobrazovaniya peremennyh. Interesno, chto v avtomodel'nyh peremennyh uravnenie renormgrushgy okazyvaetsya tozhdestvennym odnomernomu uravneniyu perenosa izlucheniya. V fizike elementarnyh chastic avtomodel'nost' vyrazhaetsya v tom, chto secheniya nekotoryh processov pri vysokih energiyah zavisyat lish' ot bezrazmernyh avtomodel'nyh kombinacii impul'sov. Obshie principy kvantovoi teorii polya dopuskayut shirokii klass takih avtomodel'nyh asimptotik.
|
Publikacii s klyuchevymi slovami:
podobie - avtomodel'nost'
Publikacii so slovami: podobie - avtomodel'nost' |

|
|
Sm. takzhe:
| |