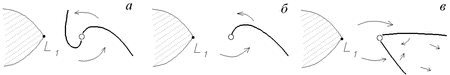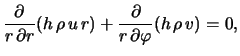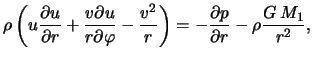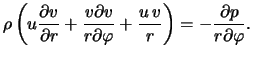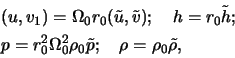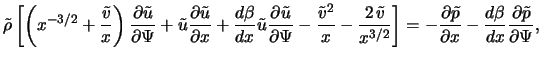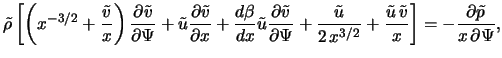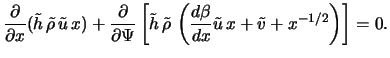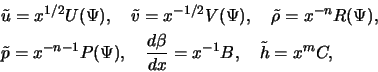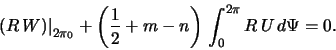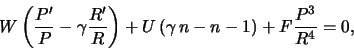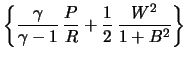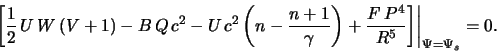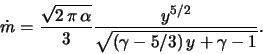<< 5.1 Osesimmetrichnaya diskovaya akkreciya | Oglavlenie | 5.3 Neustoichivosti akkrecionnyh ... >>
- 5.2.1 Gazodinamicheskoe modelirovanie peretekaniya veshestva v TDS. Usloviya obrazovaniya diska
- 5.2.2 Avtomodel'nye udarnye volny
- 5.2.3 Spiral'nye udarnye volny v TDS. Gazodinamicheskoe modelirovanie
5.2 Neosesimmetrichnaya diskovaya akkreciya
5.2.1 Gazodinamicheskoe modelirovanie peretekaniya veshestva v TDS. Usloviya obrazovaniya diska
Kak my uvideli v razd. 5.1, v ramkah osesimmetrichnyh modelei udaetsya ponyat' mnogie nablyudaemye proyavleniya AD. V to zhe vremya v tesnyh dvoinyh sistemah akkrecionnye diski yavlyayutsya principial'no neosesimmetrichnymi v silu gravitacionnogo vliyaniya so storony normal'noi zvezdy i togo, chto veshestvo popadaet v AD v forme strui cherez vnutrennyuyu lagranzhevu tochku. Esli izuchayutsya dostatochno dlitel'nye promezhutki vremeni, sushestvenno prevyshayushie period obrasheniya, to, kazalos' by, standartnye modeli AD yavlyayutsya horoshim priblizheniem. Poskol'ku veshestvo pri svoem dvizhenii k akkreciruyushemu ob'ektu delaet mnogo oborotov, to za eto vremya proishodit peremeshivanie veshestva po uglu. Gravitacionnaya sila normal'noi komponenty pri priblizhenii k kompaktnomu ob'ektu stanovitsya skol' ugodno maloi po sravneniyu s siloi, obuslovlennoi central'noi massoi.
Voznikaet ryad interesnyh voprosov: pri kakih usloviyah v TDS voznikaet AD? Kakaya chast' veshestva teryaetsya sistemoi? Budet li veshestvo akkrecirovat' bez vyazkosti? Zadachi takogo roda yavlyayutsya dlya lyubitelei analiticheskih reshenii prakticheski nerazreshimymi v silu nestacionarnosti i neodnomernosti. I pochti edinstvennyi vyhod -- chislennoe modelirovanie.
Veshestvo mozhet pokidat' opticheskuyu zvezdu v forme zvezdnogo vetra, t.e. so vsei poverhnosti zvezdy. Drugoi rezhim mozhet voznikat' pri zapolnenii normal'noi zvezdoi svoei kriticheskoi oblasti Rosha, kogda veshestvo istekaet v forme strui cherez dostatochno maluyu okrestnost' vnutrennei tochki Lagranzha. Pri etom esli skorost' gaza dostatochno velika, to trudno ozhidat' obrazovaniya diska.
Iz samyh obshih soobrazhenii yasno, chto pri akkrecii v TDS vozmozhno vozniknovenie udarnyh voln. Birman [436], po-vidimomu, byl pervym, kto v ramkah gidrodinamicheskogo podhoda rassmotrel techenie gaza v blizkoi dvoinoi sisteme v rezhime zvezdnogo vetra. Metodom harakteristik bylo rassmotreno tol'ko sverhzvukovoe techenie. Zavedomo takoe reshenie ne mozhet soderzhat' udarnyh voln. V rabote [437] poluchena konicheskaya udarnaya volna za akkreciruyushim ob'ektom. Odnako ispol'zuemyi metod konechnyh raznostei, imeyushii pervyi poryadok tochnosti, privodit k slishkom bol'shoi chislennoi vyazkosti. Krome togo, dekartova setka ne pozvolyaet pravil'no zadat' granichnye usloviya na poverhnosti obeih zvezd.
V rabotah [438-444] primenyalis' chislennye shemy
vtorogo poryadka na krivolineinoi setke, koordinatnye linii kotoroi
blizki k izoliniyam effektivnogo potenciala sistemy, sostoyashei iz
dvuh tel (
![]() ), nahodyashihsya na rasstoyanii
), nahodyashihsya na rasstoyanii ![]() drug ot druga
i vrashayushihsya s uglovoi skorost'yu
drug ot druga
i vrashayushihsya s uglovoi skorost'yu ![]() . Odna iz zvezd zapolnyaet svoyu
kriticheskuyu oblast' Rosha, a radius drugoi ne prevyshaet
. Odna iz zvezd zapolnyaet svoyu
kriticheskuyu oblast' Rosha, a radius drugoi ne prevyshaet ![]() .
Effekty, svyazannye s ohlazhdeniem, nagrevom,
vyazkost'yu5.7 i
magnitnymi polyami, ne prinimalis' vo vnimanie. Na poverhnosti
normal'noi zvezdy zadavalis' znacheniya plotnosti
.
Effekty, svyazannye s ohlazhdeniem, nagrevom,
vyazkost'yu5.7 i
magnitnymi polyami, ne prinimalis' vo vnimanie. Na poverhnosti
normal'noi zvezdy zadavalis' znacheniya plotnosti ![]() i skorosti
zvuka
i skorosti
zvuka ![]() .
.
Issledovaniyu techenii pri razlichnyh
![]() posvyasheny raboty
[439,442] dlya
posvyasheny raboty
[439,442] dlya ![]() . Esli skorost' zvuka mala (
. Esli skorost' zvuka mala (
![]() ),
to vokrug kompaktnogo ob'ekta voznikaet disk s dvumya spiral'nymi udarnymi
volnami5.8(ris. 5.5, a). Maksimal'noe chislo Maha
),
to vokrug kompaktnogo ob'ekta voznikaet disk s dvumya spiral'nymi udarnymi
volnami5.8(ris. 5.5, a). Maksimal'noe chislo Maha
![]() ne
prevyshaet
ne
prevyshaet ![]() . V sluchae
. V sluchae
![]() proishodit
perestroika techeniya:
disk stanovitsya menee vyrazhennym, pri etom ostaetsya tol'ko odna
spiral'naya udarnaya volna (ris. 5.5, b). Pri znacheniyah
proishodit
perestroika techeniya:
disk stanovitsya menee vyrazhennym, pri etom ostaetsya tol'ko odna
spiral'naya udarnaya volna (ris. 5.5, b). Pri znacheniyah ![]() , lezhashih v
oblasti
, lezhashih v
oblasti
![]() , voznikaet konicheskaya udarnaya volna
(ris. 5.5, v), vnutri konusa techenie stanovitsya sushestvenno
dozvukovym. Pri dal'neishem uvelichenii skorosti zvuka
(
, voznikaet konicheskaya udarnaya volna
(ris. 5.5, v), vnutri konusa techenie stanovitsya sushestvenno
dozvukovym. Pri dal'neishem uvelichenii skorosti zvuka
(
![]() )
obrazuetsya yarko vyrazhennyi rezhim zvezdnogo vetra. S rostom
skorosti zvuka na poverhnosti zvezdy-donora ugol mezhdu udarnymi
volnami stanovitsya men'she. Prohodya cherez konicheskuyu udarnuyu volnu,
skorost' gaza sil'no umen'shaetsya i chast' ego akkreciruet na
kompaktnyi ob'ekt. Bol'shaya chast' veshestva iz sistemy uhodit.
Pohozhie rezul'taty polucheny v rabote [445].
)
obrazuetsya yarko vyrazhennyi rezhim zvezdnogo vetra. S rostom
skorosti zvuka na poverhnosti zvezdy-donora ugol mezhdu udarnymi
volnami stanovitsya men'she. Prohodya cherez konicheskuyu udarnuyu volnu,
skorost' gaza sil'no umen'shaetsya i chast' ego akkreciruet na
kompaktnyi ob'ekt. Bol'shaya chast' veshestva iz sistemy uhodit.
Pohozhie rezul'taty polucheny v rabote [445].
Takim obrazom, tip akkreciruyushego techeniya (istechenie s
obrazovaniem diska ili v forme zvezdnogo vetra s vozniknoveniem
konicheskoi udarnoi volny) v sisteme s zapolnivshei svoyu polost'
Rosha zvezdoi-donorom opredelyaetsya znacheniem parametra
![]() . Tipichnoi dlya rassmatrivaemyh sistem yavlyaetsya ocenka
. Tipichnoi dlya rassmatrivaemyh sistem yavlyaetsya ocenka
![]() sm/s, chto sootvetstvuet temperature
sm/s, chto sootvetstvuet temperature ![]() K.
V otsutstvie zvezdnoi korony temperatura istekayushego iz zvezdy veshestva
mnogo men'she
K.
V otsutstvie zvezdnoi korony temperatura istekayushego iz zvezdy veshestva
mnogo men'she ![]() K. Sledovatel'no, naibolee veroyaten rezhim istecheniya
cherez vnutrennyuyu tochku Lagranzha s obrazovaniem akkrecionnogo diska
vokrug kompaktnogo ob'ekta. Pri peretekanii veshestva cherez
vnutrennyuyu tochku Lagranzha velik udel'nyi uglovoi moment veshestva,
chto privodit k obrazovaniyu diska. V sluchae zvezdnogo vetra
udel'nyi uglovoi moment dostatochno mal i disk ne obrazuetsya [144].
K. Sledovatel'no, naibolee veroyaten rezhim istecheniya
cherez vnutrennyuyu tochku Lagranzha s obrazovaniem akkrecionnogo diska
vokrug kompaktnogo ob'ekta. Pri peretekanii veshestva cherez
vnutrennyuyu tochku Lagranzha velik udel'nyi uglovoi moment veshestva,
chto privodit k obrazovaniyu diska. V sluchae zvezdnogo vetra
udel'nyi uglovoi moment dostatochno mal i disk ne obrazuetsya [144].
5.2.2 Avtomodel'nye udarnye volny
Predpolozhenie o tom, chto v gazovyh diskah, vrashayushihsya vokrug
kompaktnyh ob'ektov, mogut voznikat' spiral'nye udarnye volny,
vyskazyvalos' neodnokratno [446,447]. Prityagatel'nost' ih izucheniya
svyazana s tem, chto spiral'nye udarnye volny mogut perenosit'
uglovoi moment iz vnutrennih oblastei diska vo vneshnie. V tonkih
akkrecionnyh diskah (![]() ) techenie yavlyaetsya sverhzvukovym, chto
dopuskaet vozmozhnost' vozniknoveniya udarnyh voln. Prichinami
vozniknoveniya udarnyh voln mogut yavlyat'sya vtoraya komponenta v
sisteme libo asimmetrichnaya magnitosfera vokrug kompaktnogo
ob'ekta [448]. Blagodarya dissipativnym processam na fronte volny
veshestvo mozhet po spirali padat' na centr.
) techenie yavlyaetsya sverhzvukovym, chto
dopuskaet vozmozhnost' vozniknoveniya udarnyh voln. Prichinami
vozniknoveniya udarnyh voln mogut yavlyat'sya vtoraya komponenta v
sisteme libo asimmetrichnaya magnitosfera vokrug kompaktnogo
ob'ekta [448]. Blagodarya dissipativnym processam na fronte volny
veshestvo mozhet po spirali padat' na centr.
Rassmotrim stacionarnoe techenie, soderzhashee dve i bolee
spiralevidnye udarnye volny, v ramkah avtomodel'nogo podhoda [449].
Zapishem stacionarnye uravneniya gazodinamiki v sleduyushei forme:
Budem polagat', chto polutolshina
Pervyi sluchai sootvetstvuet strogo dvumernomu techeniyu v ploskosti diska. Vo-vtorom prinimaetsya, chto gaz nahoditsya v gidrostaticheskom ravnovesii v
gde
V sluchae termodinamicheskogo ravnovesiya dlya bol'shoi opticheskoi tolshiny
Schitaem, chto neprozrachnost'
Pol'zuemsya bezrazmernymi velichinami, kotorye pometim sverhu znachkom ``
gde
funkciya
S uchetom (5.2.9)-(5.2.12) uravneniya (5.2.1)-(5.2.3) primut vid
Resheniya ishem v avtomodel'nom vide
gde ![]() ,
, ![]() ,
, ![]() ,
, ![]() -- postoyannye. Esli
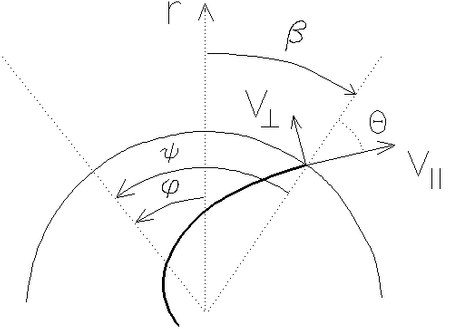
-- postoyannye. Esli ![]() est' ugol mezhdu kasatel'noi k spirali (
est' ugol mezhdu kasatel'noi k spirali (![]() const) i radial'nym
napravleniem (ris. 5.6), to
const) i radial'nym
napravleniem (ris. 5.6), to
Kak vidim, parametr
zdes'
Pervoe slagaemoe v (5.2.23) ravno nulyu. Vtoroi chlen opredelyaet temp akkrecii, kotoryi otlichen ot nulya v sluchae nalichiya udarnyh voln. Sledovatel'no,
Itak, v sluchae
Dlya sohraneniya avtomodel'nosti uravneniya (5.2.6) s uchetom (5.2.7), (5.2.8), (5.2.13) neobhodimo polozhit'
gde
Zdes'
Sistemu uravnenii (5.2.20 ![]() 5.2.22), (5.2.26) otnositel'no
neizvestnyh
5.2.22), (5.2.26) otnositel'no
neizvestnyh ![]() ,
, ![]() ,
, ![]() ,
, ![]() neobhodimo dopolnit' granichnymi usloviyami.
Rassmotrim
neobhodimo dopolnit' granichnymi usloviyami.
Rassmotrim ![]() odinakovyh udarnyh voln, razdelennyh fiksirovannym
uglom
odinakovyh udarnyh voln, razdelennyh fiksirovannym
uglom ![]() , togda resheniya dolzhny byt' periodichny s periodom
, togda resheniya dolzhny byt' periodichny s periodom
![]() . Zapishem vyrazheniya dlya normal'noi i kasatel'noi
k linii
. Zapishem vyrazheniya dlya normal'noi i kasatel'noi
k linii ![]() komponent skorosti (ris. 5.6)
komponent skorosti (ris. 5.6)
Takim obrazom, normal'naya komponenta potoka veshestva proporcional'na velichine
Zdes' cherez
gde
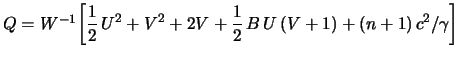 ,
,
Usloviya (5.2.31)-(5.2.33), (5.2.35) opredelyayut postoyannye integrirovaniya uravnenii (5.2.20), (5.2.21), (5.2.25), (5.2.26).
V predel'nom sluchae bol'shogo chisla udarnyh voln mozhno reshit'
zadachu analiticheski [449]. Rassmotrim tol'ko adiabaticheskoe
techenie [![]() v (5.2.26)]. Esli ishodit' iz malosti parametra
v (5.2.26)]. Esli ishodit' iz malosti parametra
![]() i predpolozheniya o tom, chto funkcii
i predpolozheniya o tom, chto funkcii ![]() yavlyayutsya lineinymi mezhdu udarnymi volnami, to mozhno zapisat' sootnoshenie
mezhdu
yavlyayutsya lineinymi mezhdu udarnymi volnami, to mozhno zapisat' sootnoshenie
mezhdu ![]() i uglom spirali
i uglom spirali ![]() [449]:
[449]:
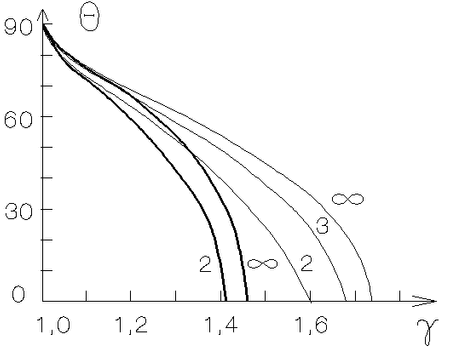 |
Ris. 5.7. Zavisimost' ugla |
Chislennyi podhod k resheniyu sformulirovannoi vyshe zadachi
pozvolyaet rassmatrivat' proizvol'noe chislo udarnyh voln, v tom
chisle s uchetom radiacionnyh poter'. Rezul'taty takogo roda
raschetov privedeny na ris. 5.7. Vklyuchenie radiacionnyh poter'
pozvolyaet ocenit' effektivnyi ![]() -parametr, figuriruyushii v "vyazkih
osesimmetrichnyh modelyah" (sm. razd. 5.1). Esli opredelit' srednii
radial'nyi potok
-parametr, figuriruyushii v "vyazkih
osesimmetrichnyh modelyah" (sm. razd. 5.1). Esli opredelit' srednii
radial'nyi potok
to, sravnivaya s rezul'tatom, vytekayushim iz standartnoi modeli AD
poluchim
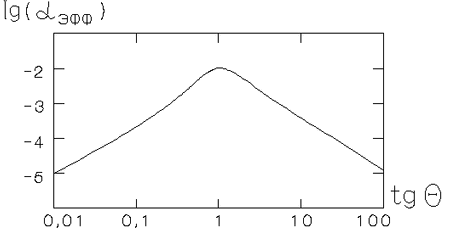
Na ris. 5.8 pokazan koefficient
![]() kak funkciya ugla
kak funkciya ugla ![]() .
V sluchae dvuh udarnyh voln (
.
V sluchae dvuh udarnyh voln (![]() ) imeetsya maksimum pri
) imeetsya maksimum pri
![]() i
i
![]() .
.
5.2.3 Spiral'nye udarnye volny v TDS. Gazodinamicheskoe modelirovanie
V p. 5.2.1 uzhe upominalis' nekotorye rezul'taty chislennogo gazodinamicheskogo modelirovaniya peretekaniya veshestva v tesnoi dvoinoi sisteme. Obsudim zdes' podrobnee problemu spiral'nyh udarnyh voln v gazovom diske, iniciirovannyh gravitacionnym potencialom sputnika -- normal'noi zvezdoi.
Prezhde vsego, v rabotah [438,439] bylo pokazano, chto:
- gaz teryaetsya normal'noi zvezdoi cherez okrestnost' tochki
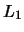 v
forme sverhzvukovoi strui (sm. ris. 1.2);
v
forme sverhzvukovoi strui (sm. ris. 1.2);
- osnovnaya chast' veshestva vrashaetsya vokrug kompaktnogo ob'ekta v
forme akkrecionnogo kol'ca/diska;
- v rezul'tate prilivnogo vzaimodeistviya obrazuetsya dve ili tri
spiralevidnye udarnye volny (UV);
- gaz nagrevaetsya v UV, teryaet svoi uglovoi moment otnositel'no
akkreciruyushei zvezdy. Kolichestvo uglovogo momenta, teryaemogo v UV,
bol'she, chem iz-za chislennoi (shemnoi) vyazkosti;
- sistema mozhet teryat' znachitel'nuyu chast' veshestva cherez tochku
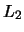 ;
;
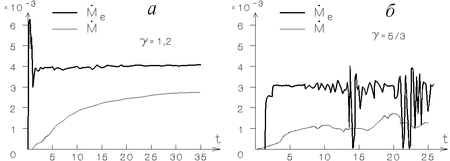
- velichina tempa poteri veshestva opticheskoi zvezdoi
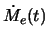 mozhet
dostatochno sil'no oscillirovat', v to vremya kak temp akkrecii
mozhet
dostatochno sil'no oscillirovat', v to vremya kak temp akkrecii
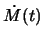 yavlyaetsya bolee gladkoi funkciei (ris. 5.9);
yavlyaetsya bolee gladkoi funkciei (ris. 5.9);
- otnoshenie
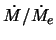 sil'no zavisit ot parametrov sistemy i
sostavlyaet
sil'no zavisit ot parametrov sistemy i
sostavlyaet 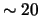 -90%.
-90%.
Prichinoi vozniknoveniya udarnyh voln yavlyaetsya vtoraya
komponenta, t.e. generator nahoditsya na periferii AD, tem samym
voznikaet vopros o tom, kak blizko k akkreciruyushemu ob'ektu mogut
prostirat'sya UV. Dlya resheniya etoi problemy byla provedena seriya
eksperimentov [440], v kotoryh razmer kompaktnogo ob'ekta ravnyalsya
![]() . Poskol'ku dlya tesnyh dvoinyh s periodom ot neskol'kih
chasov do dnei velichina
. Poskol'ku dlya tesnyh dvoinyh s periodom ot neskol'kih
chasov do dnei velichina ![]() sostavlyaet
sostavlyaet
![]() sm, to
sm, to
![]() sm, chto sootvetstvuet radiusu belogo karlika.
Esli kompaktnym ob'ektom yavlyaetsya neitronnaya zvezda s magnitnym polem
sm, chto sootvetstvuet radiusu belogo karlika.
Esli kompaktnym ob'ektom yavlyaetsya neitronnaya zvezda s magnitnym polem ![]() Gs, to disk razrushaetsya na rasstoyanii
Gs, to disk razrushaetsya na rasstoyanii
![]() sm
[451]. Raschety ubeditel'no prodemonstrirovali, chto udarnye volny
prostirayutsya vplot' do
sm
[451]. Raschety ubeditel'no prodemonstrirovali, chto udarnye volny
prostirayutsya vplot' do ![]() .
.
Obsudim vliyanie chislennoi vyazkosti. Ispol'zuemye chislennye
shemy dlya resheniya uravnenii gazodinamiki imeyut II poryadok tochnosti
i dayut shemnoe chislo Reinol'dsa
![]() (
(![]() -- razmer yacheiki). Vblizi kompaktnogo ob'ekta
-- razmer yacheiki). Vblizi kompaktnogo ob'ekta ![]() . Takim
obrazom, uglovoi moment otvoditsya naruzhu i gaz padaet na centr
dazhe v sluchae osesimmetrichnogo potenciala (bez udarnyh voln). Effekt
chislennoi vyazkosti mozhno snizit', umen'shaya velichinu
. Takim
obrazom, uglovoi moment otvoditsya naruzhu i gaz padaet na centr
dazhe v sluchae osesimmetrichnogo potenciala (bez udarnyh voln). Effekt
chislennoi vyazkosti mozhno snizit', umen'shaya velichinu ![]() .
Dlya otveta na vopros: kakaya chast' uglovogo momenta teryaetsya v UV, byl
postavlen eksperiment [438], v kotorom v moment vremeni
.
Dlya otveta na vopros: kakaya chast' uglovogo momenta teryaetsya v UV, byl
postavlen eksperiment [438], v kotorom v moment vremeni
![]() (disk nahoditsya v sostoyanii kvazistacionara) kazhdaya prostranstvennaya
yacheika v radial'nom napravlenii delilas' popolam i raschet
prodolzhalsya do
(disk nahoditsya v sostoyanii kvazistacionara) kazhdaya prostranstvennaya
yacheika v radial'nom napravlenii delilas' popolam i raschet
prodolzhalsya do
![]() . V celom global'naya struktura techeniya ne
izmenyalas', a usrednennaya velichina
. V celom global'naya struktura techeniya ne
izmenyalas', a usrednennaya velichina
![]() umen'shalas' ot
umen'shalas' ot
![]() do
do ![]() . Takim obrazom, po ocenkam avtorov okolo 60
. Takim obrazom, po ocenkam avtorov okolo 60![]() 70 % obshih poter' uglovogo momenta svyazany s udarnymi volnami.
70 % obshih poter' uglovogo momenta svyazany s udarnymi volnami.
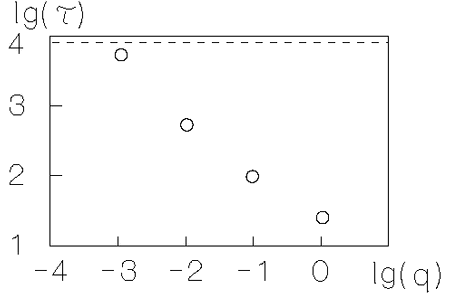
Process akkrecii udobno harakterizovat' vremenem akkrecii
![]() (
(![]() -- massa diska). Na ris. 5.10 pokazana
eksperimental'naya zavisimost' velichiny
-- massa diska). Na ris. 5.10 pokazana
eksperimental'naya zavisimost' velichiny ![]() ot otnosheniya mass komponent
ot otnosheniya mass komponent
![]() [443]. Gorizontal'naya liniya sootvetstvuet osesimmetrichnoi
modeli (
[443]. Gorizontal'naya liniya sootvetstvuet osesimmetrichnoi
modeli (![]() ), v kotoroi akkreciya polnost'yu obuslovlena chislennoi
vyazkost'yu. V ramkah vyazkoi standartnoi modeli AD velichina
), v kotoroi akkreciya polnost'yu obuslovlena chislennoi
vyazkost'yu. V ramkah vyazkoi standartnoi modeli AD velichina
![]() (p. 5.1.1). Dlya vyazkosti
(p. 5.1.1). Dlya vyazkosti
![]() imeem
imeem
V perechislennyh vyshe rabotah v raschety ne vklyuchalis' radiacionnye poteri, chto privodilo k vysokoi temperature, blizkoi k virial'noi. Uchet processov ohlazhdeniya dolzhen, s odnoi storony, uvelichit' harakternoe chislo Maha. S drugoi storony, v ramkah avtomodel'nogo podhoda (p. 5.2.2) s umen'sheniem temperatury umen'shaetsya amplituda udarnyh voln. Vyyasnenie roli etih faktorov eshe trebuet analiza.
Obsudim rezul'taty, vytekayushie iz opisannogo vyshe
gazodinamicheskogo modelirovaniya, v sravnenii s avtomodel'nymi
resheniyami (p. 5.2.2). Iz ris. 5.7 vidno, chto stacionarnye
avtomodel'nye resheniya, soderzhashie dve spiral'nye UV v diske
postoyannoi tolshiny, nevozmozhny dlya
![]() . Chislennoe
modelirovanie pri
. Chislennoe
modelirovanie pri ![]() privodit k sil'no oscilliruyushim techeniyam
(sm. ris. 5.9), t.e. stacionarnye resheniya takzhe ne poluchayutsya. Pri
privodit k sil'no oscilliruyushim techeniyam
(sm. ris. 5.9), t.e. stacionarnye resheniya takzhe ne poluchayutsya. Pri
![]() oscillyacii maly (ris. 5.9), i neposredstvennoe
sopostavlenie ugla spirali
oscillyacii maly (ris. 5.9), i neposredstvennoe
sopostavlenie ugla spirali ![]() avtomodel'noi volny s
eksperimental'nymi rezul'tatami daet udovletvoritel'noe soglasie.
Sravneniyu rezul'tatov chislennogo modelirovaniya udarnyh voln,
avtomodel'nyh reshenii i standartnoi teorii diskovoi akkrecii
posvyashena rabota [444]. Zavisimost' ugla zakrutki UV
avtomodel'noi volny s
eksperimental'nymi rezul'tatami daet udovletvoritel'noe soglasie.
Sravneniyu rezul'tatov chislennogo modelirovaniya udarnyh voln,
avtomodel'nyh reshenii i standartnoi teorii diskovoi akkrecii
posvyashena rabota [444]. Zavisimost' ugla zakrutki UV ![]() ot
pokazatelya adiabaty5.9 pokazana na
ris. 5.11. Izmereniya
ot
pokazatelya adiabaty5.9 pokazana na
ris. 5.11. Izmereniya ![]() otnosyatsya k vnutrennei zone AD, gde vliyanie
vtoroi komponenty minimal'no. V oblasti
otnosyatsya k vnutrennei zone AD, gde vliyanie
vtoroi komponenty minimal'no. V oblasti
![]() imeetsya
horoshee soglasie. V chislennyh eksperimentah pri
imeetsya
horoshee soglasie. V chislennyh eksperimentah pri
![]() dve stacionarnye udarnye volny ne poyavlyalis', avtomodel'nyi
podhod takzhe zapreshaet ih sushestvovanie pri
dve stacionarnye udarnye volny ne poyavlyalis', avtomodel'nyi
podhod takzhe zapreshaet ih sushestvovanie pri
![]() (sm.
ris. 5.7, 5.11). V oblasti
(sm.
ris. 5.7, 5.11). V oblasti
![]() vozmozhny stacionarnye
resheniya s chislom UV bol'she dvuh. Na ris. 5.12 pokazany radial'nye zavisimosti
chisla Maha udarnoi volny
vozmozhny stacionarnye
resheniya s chislom UV bol'she dvuh. Na ris. 5.12 pokazany radial'nye zavisimosti
chisla Maha udarnoi volny ![]() . Nablyudaetsya sushestvennoe razlichie po
sravneniyu s avtomodel'nymi resheniyami vo vneshnei oblasti AD, kotoroe
umen'shaetsya pri priblizhenii k centru. Takoe povedenie, po-vidimomu, vyzvano
tem, chto prilivnoe vzaimodeistvie pri postroenii avtomodel'nyh reshenii
ne uchityvalos'.
. Nablyudaetsya sushestvennoe razlichie po
sravneniyu s avtomodel'nymi resheniyami vo vneshnei oblasti AD, kotoroe
umen'shaetsya pri priblizhenii k centru. Takoe povedenie, po-vidimomu, vyzvano
tem, chto prilivnoe vzaimodeistvie pri postroenii avtomodel'nyh reshenii
ne uchityvalos'.
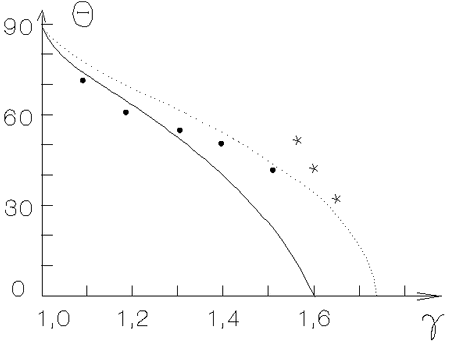 |
Ris. 5.11. Zavisimosti ugla |
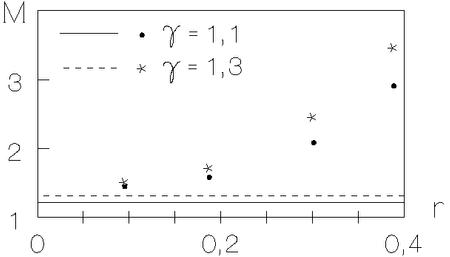 |
Ris. 5.12. Zavisimost' chisla Maha udarnoi volny ot radial'noi koordinaty. Liniyami pokazany avtomodel'nye resheniya. |
Udivitel'nym, na pervyi vzglyad, aspektom vysheopisannyh
rezul'tatov yavlyaetsya vozmozhnost' akkrecii bez radiacionnyh poter'.
V protivopolozhnost' etomu v ramkah standartnoi diskovoi akkrecii
vsya dissipiruyushaya energiya vysvechivaetsya. V svyazi s etim rassmotrim
avtomodel'nye volny s radiaciei (p. 5.2.2). Zavisimost' temperatury
ot tempa akkrecii v sluchae gidrostaticheskogo ravnovesiya v
![]() -napravlenii pokazana na ris. 5.13. Zdes' bezrazmernyi temp
akkrecii
-napravlenii pokazana na ris. 5.13. Zdes' bezrazmernyi temp
akkrecii ![]() opredelen sleduyushim obrazom
opredelen sleduyushim obrazom
 |
Ris. 5.13. Zavisimost'
bezrazmernoi temperatury
|
Uravnenie (5.1.17), vyrazhayushee balans energii, zapishem dlya
stacionarnogo sluchaya v vide
Esli predpolozhit'
gde
Zavisimosti
Iz (5.2.47) sleduet, chto adiabaticheskaya akkreciya vozmozhna tol'ko dlya
Sovershenno ochevidno, chto obsuzhdaemye zdes' udarnye volny ves'ma shodny s rassmatrivaemymi v teorii spiral'noi struktury galaktik. Rassmotrim (vozmozhno slabyi) istochnik neosesimmetrichnyh vozmushenii vo vneshnei oblasti diska. Im mozhet yavlyat'sya ne tol'ko vtoraya komponenta, no i, naprimer, kakaya-libo neustoichivost'. Takoe vozmushenie rasprostranyaetsya po disku, prinimaya spiral'nuyu formu blagodarya differencial'nosti vrasheniya. Volny v takoi situacii perenosyat uglovoi moment, vzaimodeistvuya s veshestvom diska. Eta problema shiroko obsuzhdalas' v prilozhenii k galaktikam [453,454,455].
V zaklyuchenie otmetim, chto vybor mehanizma otvoda uglovogo momenta (turbulentnaya vyazkost' ili spiral'nye udarnye volny) iz AD na osnove nablyudenii v principe vozmozhen. Naibol'shie razlichiya dolzhny voznikat' v ul'trafioletovoi chasti spektra, odnako mogut byt' obnaruzheny tol'ko dostatochno sil'nye udarnye volny [456].
<< 5.1 Osesimmetrichnaya diskovaya akkreciya | Oglavlenie | 5.3 Neustoichivosti akkrecionnyh ... >>
|
Publikacii s klyuchevymi slovami:
akkrecionnyi disk - disk, galakticheskii - gidrodinamika - spiral'naya struktura
Publikacii so slovami: akkrecionnyi disk - disk, galakticheskii - gidrodinamika - spiral'naya struktura | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |