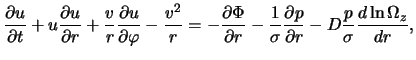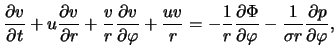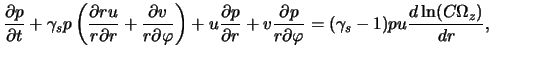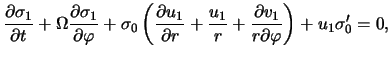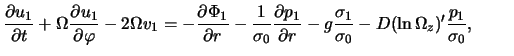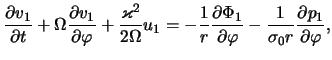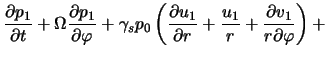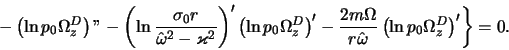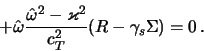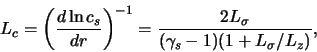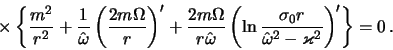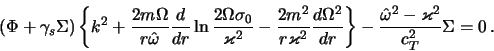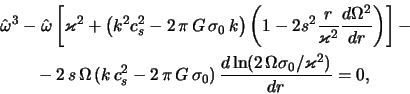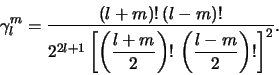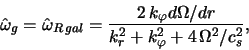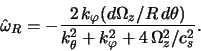<< 4.1 Ravnovesnye gazovye diski | Oglavlenie | 4.3 Neustoichivosti gazovogo grav... >>
4.2 Dinamika vozmushenii v ploskosti diska
4.2.1 Postanovka zadachi
V sootvetstvii s provedennym v p. 4.1.2 issledovaniem postavim
zadachu izucheniya dispersionnyh svoistv neosesimmetrichnyh vozmushenii
v ploskosti tonkogo gazovogo diska [324,325]. Ishodnye uravneniya
gazodinamiki v etoi modeli v sootvetstvii s (4.1.7), (4.1.10), (4.1.15)
imeyut vid4.2
gde
, 
-- radial'naya i azimutal'naya komponenty skorosti gaza,
, 
-- poverhnostnye plotnost' i
davlenie v gazovom diske, a dissipativnye chleny opusheny (issledovaniyu
dissipativnyh effektov posvyashen razd. 4.4).
Dlya izucheniya dinamiki malyh vozmushenii linearizuem sistemu
(4.2.1)-(4.2.4). Dlya etogo predstavim vhodyashie v etu sistemu
peremennye v vide summ ravnovesnyh i vozmushennyh velichin:
V rezul'tate poluchim
gde shtrih oznachaet proizvodnuyu vdol' radial'noi koordinaty i v sootvetstvii s usloviem ravnovesiya (4.1.11),
Dopolnim sistemu (4.2.6) 
(2.2.9) linearizovannym uravneniem
Puassona
ot azimutal'noi koopdinaty
i vpemeni 
v svyazi so
stacionapnost'yu i odnopodnost'yu passmatpivaemoi pavnovesnoi modeli v
azimutal'nom nappavlenii ppedstavim v vide
Togda sistema (4.2.6)-(4.2.9), (4.2.11) pepeidet v (indeks "1" u vozmushennyh velichin opuskaem i schitaem
)
gde
,
,
,
,
,
,
,
--
izotepmicheskaya skopost' zvuka,
--
adiabaticheskaya skopost' zvuka.
Isklyuchim iz ppivedennoi vyshe sistemy vozmushennye skoposti. Dlya etogo iz
(4.2.16) nahodim
Diffepencipuya zatem (4.2.20) po padial'noi koopdinate i podstavlyaya pezul'tat vmeste s (4.2.19), (4.2.20) v (4.2.14), ppivodim (4.2.14) k vidu
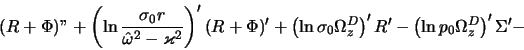
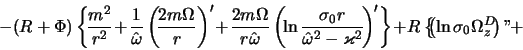
Podstavlyaya takzhe (4.2.20) v (4.2.17), poluchaem vtopoe upavnenie, svyazyvayushee
, 
, 
:
Sistema uravnenii (4.2.21), (4.2.22) vmeste s uravneniem Puassona
(4.2.18) yavlyaetsya ishodnoi dlya dal'neishego analiza dinamiki malyh
vozmushenii v modeli gazovogo diska s proizvol'nymi raspredeleniyami
, 
, 
.
4.2.2 Dispersionnoe uravnenie v izentropicheskom diske
Rassmotrim izentropicheskuyu model'. V nei
i 
opredelyaetsya sootnosheniem
gde
-- "ploskii" pokazatel' politropy (sm. p. 4.1.1).
Esli
schitat' dlya sistemy "makroatomov" gazovogo diska -- oblakov
, togda v sootvetstvii s (4.1.16)
i,
sledovatel'no,
. Otsyuda yasno, chto izentropicheskaya model'
ne ppotivopechit dannym nablyudenii po
gazovomu disku Galaktiki.
Poetomu v pervuyu ochered' provedem
dal'neishii analiz v ramkah izentropicheskoi modeli s 
(bolee
obshii sluchai budet rassmotren nizhe).
V izentropicheskoi modeli iz (4.2.22) vytekaet
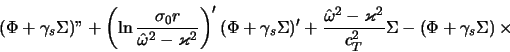
Opredelennyi progress v ponimanii fiziki gravitiruyushego
gazovogo diska, i v chastnosti v opredelenii usloviya ego
gravitacionnoi ustoichivosti otnositel'no osesimmetrichnyh
vozmushenii byl dostignut s pomosh'yu VKB-analiza v radial'nom
napravlenii. Eto obuslovleno tem obstoyatel'stvom, chto
protyazhennost' diska i harakternye masshtaby ego neodnorodnosti v
radial'nom napravlenii nastol'ko veliki po sravneniyu s ego
tolshinoi, chto naryadu s vypolneniem usloviya (4.1.18) mogut byt'
vypolneny i usloviya primenimosti VKB-priblizheniya [
-- sm. (4.2.13)]:
.
Netrudno, odnako, videt', chto VKB-priblizhenie primenimo
tol'ko k tem iz neosesimmetrichnyh vozmushenii, opisyvaemyh
uravneniem (4.2.26), dlya kotoryh vypolnyaetsya uslovie
. Takim obrazom, my mozhem izuchat' svoistva korotkovolnovyh
vozmushenii, zametno otlichayushihsya ot osesimmetrichnyh, tol'ko v nizkochastotnoi
po 
chasti spektra. Eto ogranichenie, odnako, ne yavlyaetsya,
sushestvennym dlya izucheniya gravitacionnoi neustoichivosti gazovogo
diska. Deistvitel'no, granica ustoichivosti gazovogo diska
otnositel'no osesimmetrichnyh vozmushenii opredelyaetsya iz usloviya
v minimume dispersionnoi krivoi
. Dlya resheniya voprosa ob opredelenii granicy ustoichivosti
diska otnositel'no neosesimmetrichnyh vozmushenii sleduet ishodit' iz togo,
chto v lyuboi neodnorodnoi sisteme dolzhny sushestvovat' korotkovolnovye
gradientnye vozmusheniya, maksimal'naya chastota kotoryh
, gde 
-- chastota sobstvennyh kolebanii sistemy
bez ucheta ee neodnorodnosti. Naprimer, v atmosfere Zemli chastota zvuka
, a chastota vnutrennih gravitacionnyh voln
[327], gde
-- vertikal'nyi masshtab neodnorodnosti atmosfery, 
-- uskorenie
sily tyazhesti. Analogichno v zvezdnom diske chastota dzhinsovskih vozmushenii
vezde, za isklyucheniem okrestnosti minimuma
dispersionnoi krivoi
, a maksimal'naya chastota gradientnyh
(sm. p. 2.2.4). To zhe samoe
utverzhdenie, ochevidno, spravedlivo i dlya gazovogo diska. Pri etom
granica ustoichivosti budet opredelyat'sya v oblasti "kontakta"
dzhinsovskoi i gradientnoi vetvei [minimuma dispersionnoi krivoi
], gde
. Krome togo, dispersionnye svoistva nizkochastotnyh
gradientnyh vozmushenii mogut predstavlyat' i nezavisimyi interes (sm.,
naprimer, punkty, posvyashennye volnam Rossbi i gradientno-entropiinoi
neustoichivosti).
Budem poetomu rassmatrivat' vozmusheniya, chastoty i azimutal'nye volnovye
nomera kotoryh udovletvoryayut usloviyu (4.2.28). Pri vypolnenii
etogo usloviya chleny s pervymi proizvodnymi ot i
po radial'noi koordinate v (4.2.26) okazyvayutsya prenebrezhimo malymi
po sravneniyu s pervym chlenom. Poetomu otbrasyvaya v (4.2.26) vse malye
po usloviyam (4.2.27), (4.2.28) chleny, poluchim
prihodim k iskomomu dispersionnomu uravneniyu dlya izentropicheskogo gazovogo diska
gde
-- parametr, harakterizuyushii stepen' neosesimmetrichnosti
vozmushenii.
V rabote [195] byl proveden analiz ustoichivosti tverdotel'no vrashayushegosya
(
const) gazovogo diska s plotnost'yu
gde
;
. V etoi modeli bez ispol'zovaniya VKB-priblizheniya
bylo polucheno dispersionnoe uravnenie, opisyvayushee svoistva proizvol'nyh
vozmushenii v ploskosti diska:
gde
Poskol'ku model' (4.2.32), (4.2.33) takzhe yavlyaetsya izentropicheskoi, predstavlyaet interes sravnit' dispersionnoe uravnenie (4.2.34) v korotkovolnovom
predele s
dispersionnym uravneniem (4.2.31) v tverdotel'no vrashayushemsya
predele.
V izentropicheskih modelyah
, otkuda
zaklyuchaem, chto v modeli (4.2.33)
. V korotkovolnovom predele , ispol'zuya
asimptotiku gamma-funkcii, poluchaem
i sootvetstvenno
Dlya opredeleniya analoga volnovogo chisla
zamechaem, chto [2]
Sravnivaya eto vyrazhenie s VKB-resheniem uravneniya Puassona (4.2.30), prihodim k vyvodu, chto
.
Nakonec
i poetomu uravnenie (4.2.34) mozhet byt' zapisano v vide
tozhdestvenno sovpadayushem s uravneniem (4.2.31) v predele
const.
Etot fakt sluzhit dopolnitel'nym argumentom v pol'zu korrektnosti
priblizheniya (4.2.28), ispol'zovannogo dlya VKB-analiza
dispersionnyh svoistv vozmushenii v gorazdo bolee slozhnoi, chem
(4.2.33), modeli gazovogo diska s proizvol'nymi raspredeleniyami
i .
4.2.3 Volny Rossbi
Dispersionnoe uravnenie (4.2.31) opisyvaet tri vetvi
kolebanii gazovogo diska. Esli prenebrech' neodnorodnost'yu diska i
differencial'nost'yu ego vrasheniya, to netrudno ubedit'sya, chto dve
iz nih gravitacionnye (dzhinsovskie) i ih chastoty opredelyayutsya iz
usloviya balansa kubicheskogo i lineinogo po chlenov (chastota
tret'ei vetvi v etom sluchae
). Poyavlenie tret'ego tipa
vozmushenii svyazano s neodnorodnost'yu diska i differencial'nost'yu
ego vrasheniya (proyavlenie sdvigovoi uprugosti neodnorodnoi sredy) i
ih chastota v gravitacionno ustoichivom (sm. razd. 4.3) diske mozhet
byt' priblizhenno opredelena iz usloviya balansa lineinogo po i
svobodnogo v (4.2.31) chlenov [324]:
Netrudno videt', chto 
po (4.2.37) udovletvoryaet usloviyu
(4.2.28) pri lyubyh dlinah voln vozmushenii
. Analogichnye vetvi
kolebanii, chastoty kotoryh proporcional'ny gradientam nevozmushennyh
velichin, imeyut mesto v atmosferah i okeanah planet (vnutrennie
gravitacionnye volny i volny Rossbi -- sm. [327,328], plazme
(dreifovye volny -- sm. [193], zvezdnom diske (sm. gl. 2) i drugih neodnorodnyh
sredah. Vyrazhenie (4.2.37) opisyvaet volny, imeyushie cherty kak vnutrennih
gravitacionnyh voln, tak i voln Rossbi [329]. Dlya dokazatel'stva
vtoroi chasti etogo utverzhdeniya pereidem k estestvennomu dlya
atmosfer planet predelu odnorodnoi (vdol' poverhnosti planety)
nesamogravitiruyushei sredy (formal'no
,
).
Togda, polagaya vrashenie diska slabo differencial'nym (
dlya
), iz (4.2.37) poluchaem
.
V atmosferah planet zakon dispersii korotkovolnovyh
barotropnyh vozmushenii Rossbi [328] imeet vid
Konkretnye znacheniya parametrov, harakterizuyushih dinamiku i
geometriyu upomyanutyh vyshe vihrevyh struktur, analogichnyh
planetarnym anticiklonicheskim solitonam Rossbi, v gazovyh diskah
galaktik dolzhny, ochevidno, vychislyat'sya v nelineinoi teorii. V
svyazi s etim interesna popytka pryamogo perenosa rezul'tatov teorii
solitonov Rossbi na "melkoi vode" na sluchai gazovogo diska,
predprinyataya Korchaginym i Petviashvili [330]. Poluchennyi imi
soliton imeet harakternyi radius poryadka ili bol'she
epiciklicheskogo (
) i, sledovatel'no, sootvetstvuet
vozmusheniyam s
. Ispol'zuya rezul'taty p. 4.1.2, netrudno
pokazat', chto v gravitacionno ustoichivom gazovom diske
i,
sledovatel'no,
. Takim obrazom, na strukturu i
dinamiku takogo solitona opredelyayushee vliyanie dolzhny okazyvat'
vozmusheniya gravitacionnogo potenciala, obuslovlennye vozmusheniyami
poverhnostnoi plotnosti diska (sm. razlichie dispersionnyh svoistv
planetarnyh i galakticheskih voln Rossbi v oblasti spektra
).
Ukazannoe obstoyatel'stvo podcherkivaet neobhodimost' vyyavleniya dostatochno effektivnogo i nesamopodavlyayushegosya mehanizma vozbuzhdeniya voln Rossbi v gravitiruyushih gazovyh podsistemah galaktik. Odin iz vozmozhnyh takih mehanizmov budet opisan v p. 4.3.5.
<< 4.1 Ravnovesnye gazovye diski | Oglavlenie | 4.3 Neustoichivosti gazovogo grav... >>
|
Publikacii s klyuchevymi slovami:
akkrecionnyi disk - disk, galakticheskii - gidrodinamika - spiral'naya struktura
Publikacii so slovami: akkrecionnyi disk - disk, galakticheskii - gidrodinamika - spiral'naya struktura | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |
