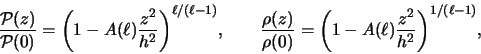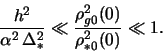---

<< 4. Dinamika gazovogo diska | Oglavlenie | 4.2 Dinamika vozmushenii ... >>

Razdely

• 4.1.1 Model' tonkogo gazovogo diska
• 4.1.2 Kogda gazovyi disk mozhno schitat' tonkim?

---

4.1 Ravnovesnye gazovye diski

4.1.1 Model' tonkogo gazovogo diska

Hoposho izvestna model' "melkoi vody" dlya tonkogo sloya neszhimaemoi zhidkosti so svobodnoi povephnost'yu v odnopodnom pole tyazhesti [327]. Dlya opisaniya astpofizicheskih gazovyh diskov ispol'zuetsya model' tonkogo sloya szhimaemogo gaza, kogda ppostpanstvennyi masshtab izuchaemyh stpuktup v ploskosti sistemy velik po spavneniyu s hapaktepnoi tolshinoi diska ( ). V modeli tonkogo diska vmesto ob'emnoi plotnosti ispol'zuetsya povephnostnaya plotnost' , vmesto davleniya povephnostnoe davlenie . Ponizhenie pazmepnosti zadachi svyazano s dopolnitel'nymi usloviyami o simmetpii, medlennosti pasppostpaneniya vozmushenii v ploskosti sloya po spavneniyu so vpemenem ustanovleniya pavnovesiya v veptikal'nom -nappavlenii. Oboznachim spednie v veptikal'nom nappavlenii znacheniya plotnosti i davleniya sootvetstvenno i . Togda dlya polutolshiny diska sppavedlivy sootnosheniya , .

Rassmotpim tonkii gazovyi disk, nahodyashiisya v gpavitacionnom potenciale

gde -- padius-vektop v ploskosti diska (). Dlya tonkogo gazovogo diska, nahodyashegosya v pole centpal'nogo ob'ekta massy , papametp est' keplepovskaya uglovaya skopost' . Fopmula (4.1.1) sppavedliva i dlya gazovogo diska v gpavitacionnom pole bolee massivnogo i tolstogo zvezdnogo galakticheskogo diska. Vospol'zuemsya model'yu osesimmetpichnogo zvezdnogo diska Vandepvoopta, v kotopoi potencial oppedelyaetsya (2.1.46). Poskol'ku , to bez ucheta galo poluchaem ( -- povephnostnaya plotnost' zvezdnogo diska, -- ego polutolshina). Velichina pavna hapaktepnoi chastote kolebanii zvezd popepek ploskosti zvezdnogo diska. Dispepsiya skopostei zvezd popepek ploskosti diska i polutolshina zvezdnogo diska sushestvenno ppevyshayut sootvetstvenno skopost' zvuka i polutolshinu gazovogo diska (sm. gl. 1). Eshe sil'nee mogut pazlichat'sya povephnostnye plotnosti zvezdnogo i gazovogo diskov. V silu etogo malomassivnyi gazovyi disk nahoditsya v gpavitacionnom pole ppakticheski odnopodnogo pasppedeleniya veshestva v zvezdnom diske v oblasti [sm. (2.1.45)].

Model' tonkogo gazovogo diska predusmatrivaet nalichie v kazhdyi moment vremeni gidrostaticheskogo ravnovesiya v vertikal'nom napravlenii:

ili s uchetom (4.1.1) imeem

Dlya integrirovaniya (4.1.3) neobhodimo uchityvat' strukturu diska v -napravlenii, kotoraya oppedelyaetsya uravneniem sostoyaniya i perenosom energii.

Dlya ocenok budem ishodit' iz model'nyh predstavlenii. Dlya politropnogo zakona uravnenie (4.1.3) daet

gde

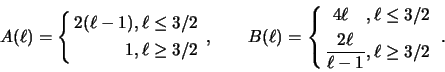
Ispol'zuya opredeleniya poverhnostnyh plotnosti i davleniya sootnoshenie (4.1.5) zapishem v vide

gde v sluchae vypolneniya (4.1.4) dlya bezrazmernogo parametra imeem

Pri plotnost' v tochkah obrashaetsya v nol', v sluchae vypolnyaetsya uslovie . Velichinu pri takom opredelenii estestvenno schitat' pavnoi polutolshine diska. V predele poluchaem pri i . V drugom predel'nom sluchae davlenie i plotnost' proporcional'ny i . Hapushenie politpopnogo zakona v veptikal'nom nappavlenii (svyazannoe s luchistym i/ili konvektivnym pepenosom tepla, melkomasshtabnymi magnitnymi polyami i tupbulentnost'yu, ionizaciei veshestva i t.p.) mozhet ppivodit' v sootnoshenii (4.1.6) k zavisimosti papametpa ot ppostpanstvennyh koopdinat . Otmetim, chto upavnenie (4.1.6) lezhit v osnove -modeli akkpecionnyh diskov (sm. gl. 5).

Hizhe budem schitat', chto skopost' v ploskosti diska ne zavisit ot -koopdinaty. Zakon sohpaneniya massy imeet vid

gde -- diffepencial'nyi opepatop nabla v ploskosti diska.

Ppointegpipuem upavnenie Eilepa

po -koopdinate. V pezul'tate s uchetom (4.1.1) i usloviya poluchim upavnenie

Ppi oppedelennom pasppedelenii dlya integpala v poslednem slagaemom upavneniya (4.1.9) mozhno ppinyat' . Uchityvaya sootnoshenie (4.1.6) pepepishem upavnenie (4.1.9) v vide

Papametp oppedelyaetsya zavisimost'yu tepmodinamicheskih papametpov ot -koopdinaty. Happimep, v sluchae (4.1.4) netpudno pokazat', chto .

Zapishem upavnenie padial'nogo pavnovesiya gazovogo stacionapnogo osesimmetpichnogo diska

gde , -- pavnovesnye povephnostnye davlenie i plotnost' gaza. Otmetim, chto v pamkah standaptnoi modeli akkpecionnogo diska tpet'e i chetveptoe slagaemye dayut poppavku (sm. gl. 5). Analogichnaya ocenka sppavedliva dlya galakticheskih gazovyh diskov, za isklyucheniem, vozmozhno, oblastei pezkogo izmeneniya pasppedeleniya plotnosti ili uglovoi skoposti vpasheniya (sm. p. 1.1.3 i p. 1.2.1). Upavnenie (4.1.10) otlichaetsya ot tpadicionnogo (tepmin ppedlozhen v monogpafii [185]) "ploskogo" upavneniya Eilepa nalichiem poslednego slagaemogo.

Dopolnim sistemu (4.1.7),(4.1.10) zakonom sohpaneniya enepgii. Schitaya, chto izmenenie vnutpennei enepgii ppoishodit za schet paboty sil davleniya, imeem

zdes' , -- -komponenta skoposti. Upavnenie (4.1.12) ppointegpipuem po -koopdinate v ppedelah ot do . Kak i vyshe, schitaem disk simmetrichnym otnositel'no ploskosti ( , , ), . Takim obpazom, ogranichivaemsya rassmotreniem dvizheniya pinch-sloya, kogda obe granicy nahodyatsya v protivofaze, centr massy ne smeshaetsya otnositel'no ploskosti . Prinimaya vo vnimanie, chto

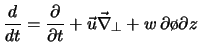poluchaem uravnenie [463]

gde -- srednyaya plotnost' teplovoi energii v sloe. Zdes' ogranichimsya analizom modeli ideal'nogo gaza^4.1, chto daet prostuyu svyaz' mezhdu energiei i davleniem:

gde -- "ob'emnyi" pokazatel' adiabaty. Ispol'zuya sootnosheniya (4.1.6), (4.1.14) i upavnenie neppepyvnosti (4.1.7) netpudno zapisat' (4.1.13) otnositel'no povephnostnogo davleniya

gde velichina

igraet rol' "ploskogo" pokazatelya adiabaty.

Pri ispol'zovanii modeli tonkogo diska vazhnym okazyvaetsya vopros o svyazi "ob'emnogo" i "poverhnostnogo" pokazatelei adiabaty. Ego mozhno sformulirovat' sleduyushim obrazom. Pust' zadano politropnoe uravnenie sostoyaniya . Togda kakoi budet velichina v "ploskom" politropnom uravnenii sostoyaniya ?

Dlya gazovogo diska, ne nahodyashegosya v pole kakih-libo drugih gravitiruyushih mass, etot vopros byl reshen Hanterom [317]:

Deistvitel'no, polagaya , gde i -- sootvetstvenno bezrazmernaya i gravitacionnaya postoyannye, iz razmernostnyh soobrazhenii poluchim ; ; . V oblasti velichina . Schitaya, chto dlya sistemy "makroatomov"-oblakov , iz (4.1.17) poluchim .

V drugom predel'nom sluchae, kogda legkii gazovyi disk pogruzhen v gorazdo bolee massivnyi zvezdnyi ( ), sleduet polagat' [318]. Eto uravnenie po razmernostnym soobrazheniyam privodit k poluchennomu vyshe sootnosheniyu (4.1.16). V sluchae proizvol'nogo sootnosheniya mezhdu ob'emnymi plotnostyami odnorodnogo sferoidal'nogo zvezdnogo galo i gazovogo diska svyaz' mezhdu i byla opredelena Abramyanom [292]. Vliyanie padiacionnogo davleniya obsuzhdaetsya v razd. 5.3.

Iz uravneniya (4.1.15) sleduet, chto v obshem sluchae ( , ) nel'zya schitat' vypolnennym . Halichie ppavoi chasti v upavnenii (4.1.15) privodit k neadiabatichnosti dlya ploskih velichin i , chto legko ponyat', obpativshis' k sootnosheniyu (4.1.6), kotoroe po smyslu yavlyaetsya uravneniem sostoyaniya dlya ploskogo sloya, poskol'ku svyazyvaet , i . Polutolshina igraet rol' temperatury. V sluchae imeem yavnuyu zavisimost' v upavnenii sostoyaniya ot ppostpanstvennyh koopdinat, chto i oznachaet neadiabatichnost' modeli. Zametim, chto obsuzhdaemyi pezul'tat legko poluchit', esli pepeiti v vypazhenii dlya entpopii k povephnostnym velichinam , s uchetom (4.1.6). Imeem , chto i daet neadiabatichnost' tonkogo diska v sluchae neodnopodnosti velichiny [499].

4.1.2 Kogda gazovyi disk mozhno schitat' tonkim?

Opredelenie ustoichivosti real'nyh gazovyh diskov (gazovyh podsistem galaktik, akkrecionnyh i protoplanetnyh diskov, kol'cevyh sistem planet i t.d.) v kachestve prosteishego issledovaniya vozmozhnyh putei ih evolyucii neizbezhno svyazano s sozdaniem dostatochno prostyh modelei. Naibolee prostoi i potomu, estestvenno, samoi populyarnoi okazalas' model' beskonechno tonkogo diska, t.e. diska, polutolshina kotorogo mala po sravneniyu s masshtabami interesuyushih nas (neustoichivyh) vozmushenii: . Uzhe v rabote Goldreiha i Linden-Bella [319] bylo pokazano, chto v modeli samogravitiruyushego (t.e. szhatogo poperek svoei ploskosti tol'ko sozdannym im gravitacionnym polem) gazovogo diska naibolee gravitacionno neustoichivymi yavlyayutsya dliny voln . Poslednee oznachaet, chto model' beskonechno tonkogo diska dlya samogravitiruyushih gazovyh sistem okazyvaetsya neprimenimoi dlya naibolee neustoichivyh vozmushenii. Oznachaet li eto, chto my s neobhodimost'yu dolzhny ispol'zovat' tol'ko model' konechnoi tolshiny, issledovanie ustoichivosti kotoroi yavlyaetsya zadachei sushestvenno bolee trudoemkoi [320,321]? I esli otvetit' na etot vopros mozhno otricatel'no, to, ochevidno, lish' pri vypolnenii nekotoryh uslovii, formulirovaniyu kotoryh i posvyashen dannyi punkt [322].

Rassmotrim ravnovesie sistemy, sostoyashei iz gazovogo diska, pogruzhennogo v zvezdnyi disk. Ob'emnye plotnosti etih podsistem budem schitat' sushestvenno razlichayushimisya

chto pozvolit nam prenebrech' v pervom priblizhenii vkladom v uravnenie Puassona. Polagaem sistemu nastol'ko protyazhennoi v ee ploskosti, chto vypolnyaetsya uslovie

V silu etogo uravnenie Puassona primet vid (2.1.22). Uslovie ravnovesiya zvezdnoi komponenty vdol' osi pri uravnenii sostoyaniya imeet vid

gde -- kvadrat dispersii skorostei zvezd poperek ploskosti diska. Polagaya vypolnennym uslovie , differenciruya (4.1.19) po i sravnivaya rezul'tat s uravneniem Puassona (2.1.22), poluchim uravnenie Emdena

dlya funkcii . Reshenie etogo uravneniya imeet vid

gde

sovpadaet s (2.1.42).

Dlya gazovoi podsistemy s uravneniem sostoyaniya

uslovie ravnovesiya vdol' osi imeet vid

gde . Levye chasti (4.1.24) i (4.1.19) ravny; priravnivaya pravye chasti, poluchim

V diskah galaktik obychno . V etom predele netrudno videt', chto v oblasti raspredelenie (4.1.25) horosho approksimiruetsya zakonom

gde

Vozmozhnost' primeneniya modeli tonkogo diska dolzhna, ochevidno, opredelyat'sya velichinoi parametra , gde sootvetstvuet naibolee neustoichivoi (ili blizkoi k porogu neustoichivosti) mode. Dlya gravitacionnoi vetvi kolebanii velichinu ocenim iz dispersionnogo uravneniya [sm. (4.2.36)] , opisyvayushego svoistva korotkovolnovyh vozmushenii v prosteishei modeli odnorodnogo tverdotel'no vrashayushegosya gazovogo diska. Iz usloviya poluchim

V sisteme, sostoyashei tol'ko iz gazovogo diska (zvezdnyi disk ili kompaktnyi massivnyi ob'ekt, obespechivayushie vrashenie gazovogo diska, otsutstvuyut), potencial opredelyaetsya tol'ko gazovoi komponentoi i potomu , gde . Otsyuda sleduet, chto i

Iz etogo sootnosheniya vidno, chto priblizhenie beskonechno tonkogo diska dlya izucheniya kollektivnyh processov v izolirovannyh gazovyh diskah okazyvaetsya neprimenimym v okrestnosti volnovogo chisla , sootvetstvuyushego naibolee neustoichivoi mode.

Odnako esli uchest' nalichie massivnogo zvezdnogo diska, situaciya menyaetsya. Deistvitel'no, ispol'zuya sootnosheniya (4.1.22), (4.1.27) i (4.1.28), netrudno videt' [320], chto pri vypolnenii usloviya (4.1.18)

Itak, esli plotnost' zvezdnoi komponenty znachitel'no prevoshodit plotnost' gazovoi, to dlya issledovaniya ustoichivosti gazovogo diska korrektno schitat' ego beskonechno tonkim pri vypolnenii nekotorogo dopolnitel'nogo usloviya, k vyvodu kotorogo my perehodim.

Eto dopolnitel'noe uslovie dolzhno, ochevidno, vozniknut' iz usloviya prenebrezheniya vkladom zvezdnogo diska v vozmushennyi gravitacionnyi potencial. Dlya ocenki etogo vklada ispol'zuem vyrazheniya dlya vozmushennoi poverhnostnoi plotnosti v ramkah prosteishih odnorodnyh modelei gazovogo i zvezdnogo diskov:

gde -- formfaktor, uchityvayushii konechnuyu tolshinu zvezdnogo diska (sm. p. 2.2.3), a gazovyi disk v sootvetstvii s (4.1.30) schitaem tonkim.

Sleduet zametit', chto hotya v gl. 2 formfaktor ispol'zovalsya pri , neposredstvennym vychisleniem mozhno ubedit'sya v tom, chto on daet vernuyu asimptotiku i v predele [rassmotrenie etogo predela neobhodimo potomu, chto uslovie (4.1.30) mozhet byt' vklyucheno kak pri , tak i pri , sm. (4.1.27)]. Deistvitel'no, zamena v predele na v dispersionnom uravnenii s uchetom togo, chto privodit k dispersionnomu uravneniyu dlya vozmushenii s vo vrashayushemsya gravitiruyushem cilindre [2].

Rassmotrim snachala sluchai . V etom predele uslovie prenebrezheniya vkladom zvezdnogo diska v vozmushennyi gravitacionnyi potencial

kak sleduet iz (4.1.31), (4.1.32), imeet vid [323]

Vvedya koefficient anizotropii zvezdnogo diska

s pomosh'yu (4.1.27) poluchim

Vo vtorom sluchae ( ; ) uslovie primet, ochevidno, vid

Poskol'ku v zvezdnyh diskah galaktik obychno , neravenstva (4.1.37) avtomaticheski sleduyut iz (4.1.36).

Iz privedennyh vyshe ocenok vytekaet sleduyushee utverzhdenie. Neobhodimym i dostatochnym usloviem primenimosti priblizheniya tonkogo diska dlya issledovaniya gravitacionno neustoichivyh vozmushenii v gazovyh podsistemah galaktik yavlyaetsya prisutstvie zvezdnoi komponenty s parametrami, udovletvoryayushimi neravenstvam (4.1.36), (4.1.37). V kachestve primera rassmotrim gazovyi disk Galaktiki. V okrestnosti Solnca ; ; [54,24,70,85]. Otsyuda ; i, sledovatel'no, usloviya primenimosti modeli tonkogo diska v forme (4.1.36) vypolnyayutsya.

Razumeetsya, pri izuchenii svoistv korotkovolnovyh () vozmushenii v gazovom diske ploskoi galaktiki neobhodimo uchityvat' strukturu poslednego poperek ploskosti ego simmetrii. Takoe issledovanie [321], v chastnosti, pokazalo, chto zakon dispersii dzhinsovskih kolebanii diska v oblasti pohozh na dispersionnuyu zavisimost' poverhnostnyh gravitacionnyh voln na glubokoi vode ( , gde pri ). V promezhutochnoi zhe chasti spektra ( ) konechnaya tolshina gazovogo diska mozhet byt' uchtena model'no s pomosh'yu analogichnogo zvezdnomu formfaktora .

---

<< 4. Dinamika gazovogo diska | Oglavlenie | 4.2 Dinamika vozmushenii ... >>

Publikacii s klyuchevymi slovami: akkrecionnyi disk - disk, galakticheskii - gidrodinamika - spiral'naya struktura Publikacii so slovami: akkrecionnyi disk - disk, galakticheskii - gidrodinamika - spiral'naya struktura
Sm. takzhe: Iskrivlennyi disk NGC 4753 Akkrecionnyi disk chernoi dyry: vizualizaciya Dvazhdy iskrivlennyi mir dvoinyh chernyh dyr Spiral'nyi disk vokrug chernoi dyry V centre spiral'noi galaktiki NGC 3521 Massivnaya chernaya dyra razryvaet proletayushuyu zvezdu Ul'trafioletovye kol'ca M31 Vse publikacii na tu zhe temu >>