<< 3.1 Modeli | Oglavlenie | 3.3 Gravitacionnaya ustoichivost' ... >>
- 3.2.1 "Global'nyi" kriterii ustoichivosti
- 3.2.2 Ustoichivost' diska otnositel'no vozbuzhdeniya bar-mody
- 3.2.3 Central'naya depressiya zvezdnoi plotnosti
- 3.2.4 Modeli s "zhivym" galo
3.2 Krupnomasshtabnaya struktura zvezdnyh diskov
3.2.1 "Global'nyi"
kriterii ustoichivosti
Rassmotrim rezul'taty eksperimentov so zvezdnym diskom bez
galo (![]() ). V takih sistemah interesnye
processy protekayut v central'noi chasti diska. Prosledim
evolyuciyu pervonachal'no osesimmetrichnoi sistemy, nahodyasheisya v
osnovnom na balanse
gravitacionnoi i centrobezhnoi sil [
). V takih sistemah interesnye
processy protekayut v central'noi chasti diska. Prosledim
evolyuciyu pervonachal'no osesimmetrichnoi sistemy, nahodyasheisya v
osnovnom na balanse
gravitacionnoi i centrobezhnoi sil [
![]() , sm. (3.1.3)]. Takaya
sistema okazyvaetsya neustoichivoi i ee razvitie zaklyuchaetsya v roste
dispersii skorostei chastic. Odnovremenno proishodit
pereraspredelenie plotnosti veshestva, skorosti vrasheniya i
iskazhenie osesimmetrichnoi formy diska v baropodobnuyu.
, sm. (3.1.3)]. Takaya
sistema okazyvaetsya neustoichivoi i ee razvitie zaklyuchaetsya v roste
dispersii skorostei chastic. Odnovremenno proishodit
pereraspredelenie plotnosti veshestva, skorosti vrasheniya i
iskazhenie osesimmetrichnoi formy diska v baropodobnuyu.
Po-vidimomu, pervaya eksperimental'naya popytka
oharakterizovat' ustoichivoe stacionarnoe sostoyanie
besstolknovitel'nogo gravitiruyushego diska odnim "global'nym"
parametrom byla predprinyata Ostraikerom i Piblsom [216]. V
kachestve takogo parametra imi byla vybrana velichina, ravnaya
polovine doli kineticheskoi energii chastic sistemy, prihodyasheisya na
ih srednee (makroskopicheskoe) dvizhenie. Poskol'ku dlya
gravitiruyushih sistem spravedliva teorema viriala v forme
![]() , gde
, gde ![]() -- kineticheskaya, a
-- kineticheskaya, a ![]() -- potencial'naya energiya
sistemy, to upomyanutyi parametr mozhno zapisat' v vide
-- potencial'naya energiya
sistemy, to upomyanutyi parametr mozhno zapisat' v vide
gde
zametno otlichayushuyusya ot
Primerno za odin-dva oborota pervonachal'no holodnyi disk
sil'no razogrevaetsya, energiya vrashatel'nogo dvizheniya perehodit v
energiyu sluchainogo dvizheniya, chto privodit k
Eksperimental'noe vychislenie parametra ![]() , uchityvayushego
nekrugovye dvizheniya chastic v diske, daet [217]
, uchityvayushego
nekrugovye dvizheniya chastic v diske, daet [217]
Rezul'tat (3.2.4) trebuet nekotorogo utochneniya, svyazannogo s
tem, chto teorema viriala dlya gravitiruyushih sistem (![]() )
neposredstvenno k eksperimental'nym modelyam ne primenima.
Deistvitel'no, n'yutonovskii potencial -- odnorodnaya funkciya
)
neposredstvenno k eksperimental'nym modelyam ne primenima.
Deistvitel'no, n'yutonovskii potencial -- odnorodnaya funkciya ![]() (
(![]() ) stepeni koordinat [52]. No ispol'zuemyi v
eksperimental'nyh modelyah potencial s myagkim "obrezaniem"
gravitacionnogo vzaimodeistviya na malyh rasstoyaniyah (sm. p. 3.1.2)
pri
) stepeni koordinat [52]. No ispol'zuemyi v
eksperimental'nyh modelyah potencial s myagkim "obrezaniem"
gravitacionnogo vzaimodeistviya na malyh rasstoyaniyah (sm. p. 3.1.2)
pri ![]() (
(![]() -- radius "obrezaniya") blizok k kvadratichnomu
potencialu (
-- radius "obrezaniya") blizok k kvadratichnomu
potencialu (![]() ). S uchetom togo, chto
). S uchetom togo, chto ![]() (
(![]() -- radius diska),
mozhno schitat', chto v srednem po disku
-- radius diska),
mozhno schitat', chto v srednem po disku
![]() , gde
, gde
![]() . Togda
. Togda
![]() ,
,
![]() -- energiya sistemy. Sravnivaya eksperimental'nye
znacheniya velichin
-- energiya sistemy. Sravnivaya eksperimental'nye
znacheniya velichin ![]() i
i
![]() , mozhno
ocenit'
, mozhno
ocenit' ![]() . Po rezul'tatam eksperimentov [217,218]
. Po rezul'tatam eksperimentov [217,218]
![]() .
.
Predstavlyaet interes vopros o vliyanii nachal'nogo
raspredeleniya poverhnostnoi plotnosti
![]() na ustoichivost'
bar-mody. Summiruya rezul'taty mnogochislennyh eksperimentov, mozhno
skazat', chto modeli, dlya kotoryh v nachal'nyi moment vremeni
harakterna ne ochen' vysokaya stepen' koncentracii massy k centru
diska, ukladyvayutsya po parametru
na ustoichivost'
bar-mody. Summiruya rezul'taty mnogochislennyh eksperimentov, mozhno
skazat', chto modeli, dlya kotoryh v nachal'nyi moment vremeni
harakterna ne ochen' vysokaya stepen' koncentracii massy k centru
diska, ukladyvayutsya po parametru ![]() v ramki, ukazannye
Ostraikerom i Piblsom [sm. (3.2.4)]. V modelyah s bolee plotnoi
central'noi chast'yu diska velichiny
v ramki, ukazannye
Ostraikerom i Piblsom [sm. (3.2.4)]. V modelyah s bolee plotnoi
central'noi chast'yu diska velichiny ![]() ,
,
![]() ,
, ![]() k koncu
eksperimentov okazyvayutsya men'shimi. Etot effekt svyazan,
po-vidimomu, s bol'shei intensivnost'yu relaksacionnyh processov v
bolee plotnyh sistemah. V eksperimentah, startuyushih iz sostoyanii s
nachal'noi dispersiei radial'nyh skorostei
k koncu
eksperimentov okazyvayutsya men'shimi. Etot effekt svyazan,
po-vidimomu, s bol'shei intensivnost'yu relaksacionnyh processov v
bolee plotnyh sistemah. V eksperimentah, startuyushih iz sostoyanii s
nachal'noi dispersiei radial'nyh skorostei
![]() [takoi disk dolzhen byt' gravitacionno ustoichiv
otnositel'no melkomasshtabnyh vozmushenii (sm. razd. 2.3)], konechnoe znachenie
parametra
[takoi disk dolzhen byt' gravitacionno ustoichiv
otnositel'no melkomasshtabnyh vozmushenii (sm. razd. 2.3)], konechnoe znachenie
parametra ![]() okazyvaetsya takim zhe, chto i v eksperimentah s
okazyvaetsya takim zhe, chto i v eksperimentah s
![]() 3.6. No s uvelicheniem
3.6. No s uvelicheniem ![]() stepen' baropodobnogo iskazheniya
diska neskol'ko umen'shaetsya, a
stepen' baropodobnogo iskazheniya
diska neskol'ko umen'shaetsya, a
![]() uvelichivaetsya primerno na
uvelichivaetsya primerno na
![]() .
.
Sootnosheniya (3.2.4), (3.2.5) oznachayut, chto ploskie gravitiruyushie sistemy bez sferoidal'nyh podsistem v stacionarnom sostoyanii dolzhny byt' dostatochno "goryachimi" -- v pekulyarnyh dvizheniyah zvezd dolzhno byt' zaklyucheno bolee poloviny ih kineticheskoi energii. V takih sistemah, kak pravilo, vozbuzhdaetsya bar-moda, a dispersiya radial'nyh skorostei chastic dazhe na periferii diska ne men'she poloviny velichiny krugovoi skorosti vrasheniya ego veshestva.
3.2.2 Ustoichivost' diska otnositel'no vozbuzhdeniya bar-mody
Nachinaya s klassifikacii galaktik Habbla stalo yasno, chto ploskie spiral'nye galaktiki mozhno razdelit' na dve gruppy. Dlya odnoi iz nih (SB) harakterno nalichie yarkoi peremychki (bara) s prikreplennymi k ego koncam (chasto pochti pod pryamym uglom) spiralyami. V drugoi gruppe ploskih galaktik (S) spirali othodyat ot obrazovaniya, raspolozhennogo v centre galaktiki. Yasno, chto issledovanie ustoichivosti gravitiruyushego diska (analiticheskoe i chislenno-eksperimental'noe) dolzhno opredelit' te faktory, kotorye prepyatstvuyut vozbuzhdeniyu bar-mody vo mnogih ploskih galaktikah.
Poskol'ku bar-moda yavlyaetsya krupnomasshtabnym vozmusheniem,
ispol'zovannoe v gl. 2 korotkovolnovoe priblizhenie dlya izucheniya ego
ustoichivosti neprimenimo. Takim obrazom, v etom sluchae neobhodimo
uchityvat' strukturu diska v celom, chto, estestvenno, nakladyvaet
dostatochno zhestkie ogranicheniya na svoistva modeli. Poetomu
detal'noe analiticheskoe issledovanie ustoichivosti bar-mody bylo
provedeno lish' v modelyah tverdotel'no vrashayushihsya diskov
[50,223,238,266].
Eti issledovaniya pokazali, chto modeli tonkogo diska bez ucheta
massy sfericheskoi podsistemy ustoichivy otnositel'no vozbuzhdeniya
bar-mody tol'ko pri
Bolee konstruktivnoi okazalas' postanovka zadachi, v kotoroi
pomimo konechnoi tolshiny diska uchityvalos' nalichie i sferoidal'noi
podsistemy. Tak, v modeli, sostoyashei iz odnorodnogo galo
(sferoidal'noi podsistemy) i odnorodnogo splyusnutogo ellipsoida
vrasheniya (diska) s bol'shoi poluos'yu ![]() i maloi poluos'yu
i maloi poluos'yu ![]() ,
bylo obnaruzheno [238], chto v diskovom predele (
,
bylo obnaruzheno [238], chto v diskovom predele (
![]() )
ellipsoid ustoichiv otnositel'no vozbuzhdeniya bar-mody pri
)
ellipsoid ustoichiv otnositel'no vozbuzhdeniya bar-mody pri
Kak uzhe govorilos' vyshe, analiticheskoe izuchenie ustoichivosti
bar-mody v differencial'no vrashayushihsya neodnorodnyh diskah
konechnoi tolshiny zatrudnitel'no. Eto, ochevidno, proshe delat' s
pomosh'yu chislennogo eksperimenta. Rannie eksperimenty (sm.,
naprimer, [211,212,216,253]) podtverdili, chto v nedostatochno goryachih
(
![]() ) tonkih diskah bez galo vozbuzhdenie
bar-mody neizbezhno. Uchet konechnoi massy galo pokazal, chto s rostom massy
poslednego bar-moda stabiliziruetsya [268-272]. V to zhe
vremya v raznyh modelyah granicy ustoichivosti bar-mody po parametru
) tonkih diskah bez galo vozbuzhdenie
bar-mody neizbezhno. Uchet konechnoi massy galo pokazal, chto s rostom massy
poslednego bar-moda stabiliziruetsya [268-272]. V to zhe
vremya v raznyh modelyah granicy ustoichivosti bar-mody po parametru
![]() zametno razlichayutsya, gruppiruyas', odnako, v okrestnosti
zametno razlichayutsya, gruppiruyas', odnako, v okrestnosti
![]() .
.
Rezul'taty eksperimentov udobno opisyvat' s pomosh'yu parametra
![]() , harakterizuyushego stepen' baropodobnogo iskazheniya
diska dlya razlichnyh raspredelenii ob'emnoi plotnosti galo
, harakterizuyushego stepen' baropodobnogo iskazheniya
diska dlya razlichnyh raspredelenii ob'emnoi plotnosti galo ![]() [218].
V modelyah bez galo
[218].
V modelyah bez galo
![]() (ris. 3.1). S rostom
massy galo parametr
(ris. 3.1). S rostom
massy galo parametr ![]() umen'shaetsya i pri
umen'shaetsya i pri
![]() stanovitsya men'she urovnya, na kotorom pogreshnost' izmereniya velichiny
stanovitsya men'she urovnya, na kotorom pogreshnost' izmereniya velichiny ![]() v dannyh eksperimentah delaet ee razlichimoi s
v dannyh eksperimentah delaet ee razlichimoi s
![]() .
.
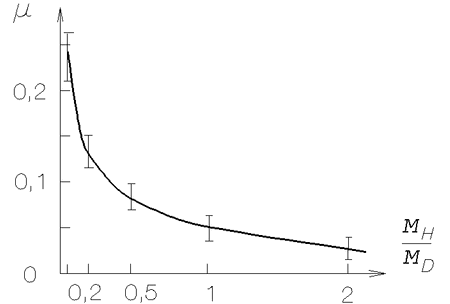 |
Ris. 3.1. Zavisimost'
|
V svyazi s privedennymi vyshe rezul'tatami predstavlyaet interes
i eksperimental'nyi kriterii [219], utverzhdayushii, chto dlya
ustoichivosti diska otnositel'no vozbuzhdeniya bar-mody dolzhno
vypolnyat'sya uslovie
![]() , gde (
, gde (
![]() -- maksimal'noe znachenie
-- maksimal'noe znachenie
![]() v diske. Po rezul'tatam eksperimentov [218] etot kriterii
proveryalsya v konechnyh kvazistacionarnyh sostoyaniyah diska. Okazalos',
chto velichina
v diske. Po rezul'tatam eksperimentov [218] etot kriterii
proveryalsya v konechnyh kvazistacionarnyh sostoyaniyah diska. Okazalos',
chto velichina ![]() izmenyaetsya ot
izmenyaetsya ot
![]() pri
pri ![]() do
do
![]() pri
pri ![]() . Takim obrazom, kriterii [219]
vyglyadit slishkom zhestkim. Prichina sostoit, po-vidimomu, v tom, chto
kriterii byl poluchen v eksperimentah, v kotoryh nachal'noe
sostoyanie diska bylo holodnym (
. Takim obrazom, kriterii [219]
vyglyadit slishkom zhestkim. Prichina sostoit, po-vidimomu, v tom, chto
kriterii byl poluchen v eksperimentah, v kotoryh nachal'noe
sostoyanie diska bylo holodnym (![]() ). V takom sostoyanii usloviya
vozbuzhdeniya bar-mody naibolee blagopriyatny, a
). V takom sostoyanii usloviya
vozbuzhdeniya bar-mody naibolee blagopriyatny, a
![]() (izmeryaemoe
v nachal'nyi moment vremeni) -- bol'she, chem v goryachem diske. Krome
togo, diski v eksperimentah [219] dvumerny, chto takzhe oblegchaet
vozbuzhdenie bar-mody. Poetomu neudivitel'no, chto ukazannyi
kriterii privodit k neobychaino nizkoi ocenke otnosheniya massy k
svetimosti (poryadka edinicy) dlya diskov Sc-galaktik [250].
Ishodya zhe iz rezul'tatov eksperimentov [218] sleduet schitat', chto
zvezdnyi disk ustoichiv otnositel'no vozbuzhdeniya bar-mody pri
(izmeryaemoe
v nachal'nyi moment vremeni) -- bol'she, chem v goryachem diske. Krome
togo, diski v eksperimentah [219] dvumerny, chto takzhe oblegchaet
vozbuzhdenie bar-mody. Poetomu neudivitel'no, chto ukazannyi
kriterii privodit k neobychaino nizkoi ocenke otnosheniya massy k
svetimosti (poryadka edinicy) dlya diskov Sc-galaktik [250].
Ishodya zhe iz rezul'tatov eksperimentov [218] sleduet schitat', chto
zvezdnyi disk ustoichiv otnositel'no vozbuzhdeniya bar-mody pri
![]() .
.
Chislennoe modelirovanie processa formirovaniya bara ostaetsya ves'ma populyarnym. No bolee pozdnie raboty v osnove svoei podtverzhdayut vysheizlozhennye rezul'taty [273,274].
Summiruya skazannoe vyshe, mozhno utverzhdat', chto SB-galaktiki ne dolzhny imet' sfericheskoi podsistemy, massa kotoroi sravnima s massoi diska, a S-galaktiki imeyut, po-vidimomu, sfericheskuyu podsistemu s massoi (v sfere radiusa vidimogo diska) bol'shei ili poryadka massy diska. Kosvennym podtverzhdeniem etogo rezul'tata mozhet sluzhit' tot fakt, chto vblizi centra skopleniya galaktik v Volosah Veroniki dolya SB-galaktik vdvoe vyshe, chem na periferii skopleniya. Naibolee estestvennaya prichina etogo -- v "sduvanii" galo pri vzaimnom sblizhenii galaktik i oslablenii vsledstvie etogo ustoichivosti ih diskov po otnosheniyu k vozbuzhdeniyu bar-mody [275]. Krome togo, faktorom, sposobstvuyushim formirovaniyu peremychki, mozhet yavlyat'sya prilivnoe vzaimodeistvie so storony massivnogo sputnika [276]. Vopros o vliyanii gazovoi podsistemy na razvitie bar-mody budet rassmotren v razd. 3.4.
Sleduet skazat', chto bar-moda ne yavlyaetsya edinstvennym
mehanizmom formirovaniya bara. V sluchae medlennogo vrasheniya sistemy
(
![]() ) voznikayut usloviya dlya razvitiya neustoichivosti
radial'nyh orbit, kotoraya neposredstvenno ne svyazana s gravitaciei
(sm. [2]). Rezul'tatom razvitiya etoi neustoichivosti mogut
yavlyat'sya peremychki v galaktikah s massivnym baldzhem i mini-bary
razmerom neskol'ko soten parsek v centre ryada ploskih galaktik
[5,277].
) voznikayut usloviya dlya razvitiya neustoichivosti
radial'nyh orbit, kotoraya neposredstvenno ne svyazana s gravitaciei
(sm. [2]). Rezul'tatom razvitiya etoi neustoichivosti mogut
yavlyat'sya peremychki v galaktikah s massivnym baldzhem i mini-bary
razmerom neskol'ko soten parsek v centre ryada ploskih galaktik
[5,277].
3.2.3 Central'naya depressiya zvezdnoi plotnosti
V gl. 1 upominalos' o takom lokal'nom fenomene, kak depressiya ("dyra") v raspredelenii poverhnostnoi plotnosti v central'nyh chastyah zvezdnyh diskov galaktik. Voznikaet estestvennyi vopros, pochemu central'naya depressiya plotnosti zvezdnogo diska ne ischezaet pod vliyaniem relaksacionnyh processov, obuslovlennyh kollektivnymi processami. V ramkah chislennogo eksperimenta eta problema rassmatrivalas' v rabotah [246,278,279].
Dlya opisaniya dinamicheskoi evolyucii glubiny depressii udobna
velichina
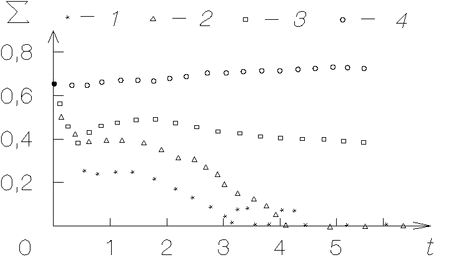 |
Ris. 3.2. Vremennaya evolyuciya glubiny depressii |
Takim obrazom, iz opisannyh vyshe eksperimentov sleduet, chto tol'ko galaktiki s massivnoi i/ili dostatochno koncentrirovannoi k centru sfericheskoi sostavlyayushei mogut imet' depressiyu zvezdnoi plotnosti. Fakticheski vyzhivanie depressii v diske zavisit ot nalichiya massivnogo baldzha, chto soglasuetsya s nablyudeniyami ryada real'nyh galaktik (sm. razd. 1.1). Zametim, chto vpervye na vozmozhnost' sushestvovaniya "deficita" poverhnostnoi plotnosti vo vnutrennei chasti ploskoi zvezdnoi podsistemy pri opredelennyh znacheniyah parametrov sfericheskoi podsistemy ukazyvalos' v rabote [191], gde etot vyvod byl sdelan na osnove raschetov ravnovesiya vrashayushegosya diska v pole galo.
V nekotoryh sluchayah nablyudeniya dopuskayut nalichie central'noi depressii plotnosti diska u galaktik pozdnih morfologicheskih tipov, u kotoryh baldzh prakticheski otsutstvuet, no imeetsya drugaya osobennost' -- peremychka. Poskol'ku bar vrashaetsya so skorost'yu, otlichnoi ot skorosti vrasheniya zvezdnogo diska, to eto mozhet privodit' k pereraspredeleniyu uglovogo momenta, chto mozhet sderzhivat' relaksaciyu central'noi "dyry". Po-vidimomu, v etom sluchae neobhodimo uchityvat' naryadu so zvezdnym diskom i gazovyi. Prichem bar ne tol'ko mozhet sderzhivat' relaksaciyu, no i byt' otvetstvennym za vozniknovenie depressii.
3.2.4 Modeli s "zhivym" galo
Kak my videli, uchet galo sushestven pri postroenii
realistichnyh modelei galaktik. Kak pravilo, schitaetsya, chto
veshestvo galo pochti ne vrashaetsya i raspredeleno simmetrichno.
Vopros o primenimosti ispol'zovaniya stacionarnogo galo pri
modelirovanii odinochnyh ploskih galaktik rassmatrivalsya Holom
[248], kotoryi rasschityval dinamicheskuyu model' disk![]() galo. Kazhdaya iz
podsistem sostoyala iz
galo. Kazhdaya iz
podsistem sostoyala iz ![]() odinakovyh tel i, sledovatel'no,
odinakovyh tel i, sledovatel'no,
![]() . Posle treh oborotov vrasheniya "zhivoe" galo ostavalos'
sfericheski simmetrichnym, a v ploskom diske bez bara nablyudalas'
spiral' s dvumya vetvyami. V dannom eksperimente obmen energiei
mezhdu galo i diskom byl mal.
. Posle treh oborotov vrasheniya "zhivoe" galo ostavalos'
sfericheski simmetrichnym, a v ploskom diske bez bara nablyudalas'
spiral' s dvumya vetvyami. V dannom eksperimente obmen energiei
mezhdu galo i diskom byl mal.
Selvud [249], vozvrashayas' k etoi probleme, otmechaet dve
prichiny, po kotorym "zhivoe" galo mozhet otlichat'sya ot sluchaya
nepodvizhnoi sfericheskoi podsistemy. Vo-pervyh, vozmozhna peredacha
uglovogo momenta diska k zvezdam galo, chto privodit k ustoichivosti
bez formirovaniya bara (Mark [280] pridaval vazhnoe znachenie obmenu
uglovym momentom mezhdu diskom i galo v vozniknovenii spiral'nyh
voln v diske). Vo-vtoryh, vozmusheniya v raspredelenii zvezd v
diskah vliyayut cherez galo na dinamiku samogo diska. Osnovnye vyvody
iz provedennyh Selvudom eksperimentov zaklyuchayutsya v sleduyushem.
Modeli s nepodvizhnym i "zhivym" galo dayut vpolne adekvatnye
rezul'taty pri issledovanii global'noi ustoichivosti. Sushestvennoe
vzaimodeistvie mezhdu dvumya podsistemami voznikaet tol'ko posle
formirovaniya sil'nogo bara. Hotya nebol'shoi obmen uglovym momentom
mezhdu diskom i galo imeetsya dazhe v prakticheski osesimmetrichnyh
sistemah, gipoteza Marka podtverzhdeniya ne nashla. Dlya stabilizacii
bar-mody neobhodimo, kak i v sluchae stacionarnogo galo,
sosredotochit'
![]() ot obshei massy v sfericheskoi
podsisteme.
ot obshei massy v sfericheskoi
podsisteme.
V rabote Litla i Karlberga [281] podrobno analiziruetsya
dlitel'naya evolyuciya sistemy, posle togo kak process formirovaniya
bara zavershen. Nablyudayutsya medlennye monotonnye izmeneniya
parametrov bara, diska i galo: period bara vyrastaet za vremya
eksperimenta (![]() let) bolee chem v dva raza, uglovoi moment
diskovoi komponenty peredaetsya sferoidal'noi, prichem v konce
eksperimenta uglovoi moment galo vsego v dva raza men'she, chem u
diska.
let) bolee chem v dva raza, uglovoi moment
diskovoi komponenty peredaetsya sferoidal'noi, prichem v konce
eksperimenta uglovoi moment galo vsego v dva raza men'she, chem u
diska.
Miller [282] izuchal dinamiku sistemy, v kotoroi sfericheskaya podsistema yavlyalas' splyushennoi i osi simmetrii diska i galo ne sovpadali. V takoi situacii centr diskovoi podsistemy vrashaetsya vokrug nekotoroi tochki.
V svyazi s obsuzhdaemym zdes' voprosom o vzaimodeistvii diska i
galo umestno upomyanut' o rabote [283], v kotoroi predpolagaetsya,
chto takoe vzaimodeistvie podsistem opredelyaetsya potokom massy,
energii, impul'sa i magnitnogo polya cherez tak nazyvaemye "dymovye
truby", obrazuyushiesya vspyshkami sverhnovyh II tipa. Odnako takogo
roda modeli v ramkah zadachi ![]() tel ne rassmatrivalis'.
tel ne rassmatrivalis'.
<< 3.1 Modeli | Oglavlenie | 3.3 Gravitacionnaya ustoichivost' ... >>
|
Publikacii s klyuchevymi slovami:
akkrecionnyi disk - disk, galakticheskii - gidrodinamika - spiral'naya struktura
Publikacii so slovami: akkrecionnyi disk - disk, galakticheskii - gidrodinamika - spiral'naya struktura | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |
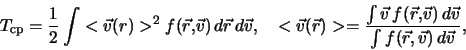
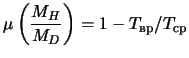 ,
harakterizuyushaya stepen' razvitiya bar-mody. V
ukazannyh na grafike intervalah pri kazhdom
znachenii
,
harakterizuyushaya stepen' razvitiya bar-mody. V
ukazannyh na grafike intervalah pri kazhdom
znachenii