Photometric Mass Estimate for the Compact Component of SS 433: And Yet It Is a Neutron Star
V. P. Goranskij
|
Peremennye Zvezdy (Variable Stars) 31, No. 5, 2011 Received October 1; accepted October 17.
Sternberg Astronomical Institute, Moscow University,
Universitetski pr., 13, Moscow, 199992, Russia;
|
Article in PDF |
1. INTRODUCTION
SS 433 (Stephenson & Sanduleak, 1977) = V1343 Aql is a unique
variable star with moving emission lines in the spectrum. Each
stationary emission of Balmer or HeI lines has two moving emission
components that are formed by a pair of oppositely directed and
highly collimated precessing relativistic jets or beams of very
hot matter accelerated to the velocity of ![]() , i.e. to
, i.e. to
![]() km/s. The period of jet precession is
162
km/s. The period of jet precession is
162![]() 5-164
5-164![]() (Margon et al., 1979; Margon, 1984). The jets
are inclined to the precession axis by 19
(Margon et al., 1979; Margon, 1984). The jets
are inclined to the precession axis by 19![]() 75, and the axis of
precession is inclined by 78
75, and the axis of
precession is inclined by 78![]() 81 to the line of sight (Davydov
et al., 2008). Like wavelengths of other moving lines, the
wavelengths of H
81 to the line of sight (Davydov
et al., 2008). Like wavelengths of other moving lines, the
wavelengths of H![]() components follow sine functions with
the full amplitudes of 1200 Å, in antiphase (Fig. 1). In this
motion, H
components follow sine functions with
the full amplitudes of 1200 Å, in antiphase (Fig. 1). In this
motion, H![]() components are superimposed in the position
located near 6800 Å twice for a precession period, at the times
usually designated
components are superimposed in the position
located near 6800 Å twice for a precession period, at the times
usually designated ![]() and
and ![]() . The wavelength where the
components coincide differs from the stationary H
. The wavelength where the
components coincide differs from the stationary H![]() -line
wavelength by 250 Å, and this is due to transverse Doppler
effect following from the special theory of relativity. The time
of the largest divergence of moving emissions is designated
-line
wavelength by 250 Å, and this is due to transverse Doppler
effect following from the special theory of relativity. The time
of the largest divergence of moving emissions is designated ![]() .
Additionally, the jets show nodding oscillations (or jitter) with
the period of 6
.
Additionally, the jets show nodding oscillations (or jitter) with
the period of 6![]() 28 (Newsom & Collins, 1981 and 1986; Wagner
et al., 1981) and amplitude of 2
28 (Newsom & Collins, 1981 and 1986; Wagner
et al., 1981) and amplitude of 2![]() 8 (Borisov & Fabrika, 1987).
The matter of jets is erupted into "bullets" that become apparent
as discrete line components in the spectra, so that each emission
detail appears at a fixed wavelength, it strengthens in a typical
time range of about 0.5-1
8 (Borisov & Fabrika, 1987).
The matter of jets is erupted into "bullets" that become apparent
as discrete line components in the spectra, so that each emission
detail appears at a fixed wavelength, it strengthens in a typical
time range of about 0.5-1![]() and decays in 1-3
and decays in 1-3![]() (Grandi &
Stone, 1982; Vermeulen et al., 1993a). Several bullets form the
composite structure of a moving emission line. The collimation
angle of a bullet is about 1
(Grandi &
Stone, 1982; Vermeulen et al., 1993a). Several bullets form the
composite structure of a moving emission line. The collimation
angle of a bullet is about 1![]() 0-1
0-1![]() 4 (Borisov & Fabrika,
1987).
4 (Borisov & Fabrika,
1987).
The details of precessing jets can be followed by radio
interferometry in the milliarcsecond scale (Vermeulen et al.,
1993b). Deep radio images were taken with the VLA radio telescope,
they show the structure of jets up to angular distances of 4
![]() (Blundell & Bowler, 2004). Fitting radio images with the
kinematical model of jets gives a sufficiently accurate distance
to SS 433, independent of interstellar absorption. This distance
is in the range between 4.85 (Vermeulen et al., 1993b, from the
VLBI) and 5.50 kpc (Hjellming & Johnson, 1982, from the VLA, and
Blundell & Bowler, 2004, from the VLA). Intermediate distance
values were measured with the same method by Spencer (1984),
MERILIN, 4.9 kpc; Fejes (1986), VLBI, 5.0 kpc; and Romney et al.
(1987), VLBI, 5.0 kpc. There is no systematical trend of distance
measures versus time, and the mean distance value is
(Blundell & Bowler, 2004). Fitting radio images with the
kinematical model of jets gives a sufficiently accurate distance
to SS 433, independent of interstellar absorption. This distance
is in the range between 4.85 (Vermeulen et al., 1993b, from the
VLBI) and 5.50 kpc (Hjellming & Johnson, 1982, from the VLA, and
Blundell & Bowler, 2004, from the VLA). Intermediate distance
values were measured with the same method by Spencer (1984),
MERILIN, 4.9 kpc; Fejes (1986), VLBI, 5.0 kpc; and Romney et al.
(1987), VLBI, 5.0 kpc. There is no systematical trend of distance
measures versus time, and the mean distance value is ![]() kpc.
kpc.
 |
Fig. 1.
Wavelengths of the H |
SS 433 is also known as an eclipsing binary system with the
orbital period of 13![]() 082 (Gladyshev et al., 1980; Gladyshev,
1981; Cherepashchuk, 1981; Crampton & Hutchings, 1981). In
kinematical jet-precession models derived from observations of the
moving lines, the axis of precession coincides with the orbital
axis, so the orbital inclination of SS 433 is measured correctly.
Photometry of SS 433 also reveals precession and nodding periods,
as well as light outbursts at different time scales (Goranskii et
al., 1998a). The shape of eclipsing light curve and its maximum
light depend on the phase of precession period (Fig. 2). Near
082 (Gladyshev et al., 1980; Gladyshev,
1981; Cherepashchuk, 1981; Crampton & Hutchings, 1981). In
kinematical jet-precession models derived from observations of the
moving lines, the axis of precession coincides with the orbital
axis, so the orbital inclination of SS 433 is measured correctly.
Photometry of SS 433 also reveals precession and nodding periods,
as well as light outbursts at different time scales (Goranskii et
al., 1998a). The shape of eclipsing light curve and its maximum
light depend on the phase of precession period (Fig. 2). Near
![]() times, it looks like that of a typical
times, it looks like that of a typical ![]() Lyrae
variable star having two minima of different depths. At other
phases of precession, the dispersion of observations increases,
but some orbital-phase averaged light curves resemble those of
Cepheids. There are pronounced brightness variations in eclipse
depth depending on the precession-period phase
Lyrae
variable star having two minima of different depths. At other
phases of precession, the dispersion of observations increases,
but some orbital-phase averaged light curves resemble those of
Cepheids. There are pronounced brightness variations in eclipse
depth depending on the precession-period phase ![]() , with the
, with the
![]() -band amplitude of 0
-band amplitude of 0![]() 4. These variations suggest that the
eclipses are partial. However, the same variations can be fitted
by the nodding period as well because the precession and nodding
periods are related to the orbital one by the formula:
4. These variations suggest that the
eclipses are partial. However, the same variations can be fitted
by the nodding period as well because the precession and nodding
periods are related to the orbital one by the formula:
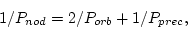 |
(1) |
 |
Fig. 2.
Evolution of the orbital light
curve with the phase of the secondary precession period. To
demonstrate the effect, the orbital-period light curves are
calculated in 12 intervals (bins) of the precession period and
displayed in the order of increasing precession phase. The
precession zero phase |
Multicolor photometry reveals peculiar behavior of SS 433 in
different filters. If the ![]() and
and ![]() color indices remain
approximately constant and independent of brightness, the
color indices remain
approximately constant and independent of brightness, the ![]() index varies with the orbital phase, being strongly correlated
with the
index varies with the orbital phase, being strongly correlated
with the ![]() or
or ![]() magnitudes. During flares or active states,
the
magnitudes. During flares or active states,
the ![]() index departs from this relation to the right side
(Gladyshev, 1981), suggesting that the deviations are connected
with a brightening of the stationary H
index departs from this relation to the right side
(Gladyshev, 1981), suggesting that the deviations are connected
with a brightening of the stationary H![]() emission. However,
observations in the
emission. However,
observations in the
![]() filters in a flare
performed by V. Rakhimov (Aslanov et al., 1993) revealed that the
amplitude of the flare in the near-infrared
filters in a flare
performed by V. Rakhimov (Aslanov et al., 1993) revealed that the
amplitude of the flare in the near-infrared ![]() filter
(
filter
(![]() = 7700 Å;
= 7700 Å;
![]() Å) was larger
than in the narrow-band H
Å) was larger
than in the narrow-band H![]() filter (
filter (![]() = 6550
Å; FWHM = 200 Å). This phenomenon was noticed by an anonymous
referee of the Astronomy and Astrophysics, so we call it
"the anonymous referee effect". The referee's finding led to a
chain of further discoveries. First, it was found that the light
curve of SS 433 consisted of two almost independent light curves
formed by two light sources having essentially different
= 6550
Å; FWHM = 200 Å). This phenomenon was noticed by an anonymous
referee of the Astronomy and Astrophysics, so we call it
"the anonymous referee effect". The referee's finding led to a
chain of further discoveries. First, it was found that the light
curve of SS 433 consisted of two almost independent light curves
formed by two light sources having essentially different ![]() color indices, 1
color indices, 1![]() 9 and 2
9 and 2![]() 8. Second, both light curves may be
easily extracted from the combined light curve. Third, the blue
source shows periodic orbital, precessing, and nodding variations,
whereas the red one is not periodic and exhibits flares that
coincide with radio flares (Goranskij et al., 1998b). It became
clear that the spectrum of the red source extended up to radio
wavelengths. Its contribution to the combined spectrum of the
system increases to longer wavelengths. The red source veils the
blue source, and therefore amplitudes of the orbital and
precession light variations decrease from
8. Second, both light curves may be
easily extracted from the combined light curve. Third, the blue
source shows periodic orbital, precessing, and nodding variations,
whereas the red one is not periodic and exhibits flares that
coincide with radio flares (Goranskij et al., 1998b). It became
clear that the spectrum of the red source extended up to radio
wavelengths. Its contribution to the combined spectrum of the
system increases to longer wavelengths. The red source veils the
blue source, and therefore amplitudes of the orbital and
precession light variations decrease from ![]() to
to ![]() bands. The contribution of the blue source is variable with the
orbital period, and this is a reason why the
bands. The contribution of the blue source is variable with the
orbital period, and this is a reason why the ![]() index varies
with the orbital phase.
index varies
with the orbital phase.
The mean ![]() and
and ![]() colors of SS 433 are respectively
0
colors of SS 433 are respectively
0![]() 90 and 2
90 and 2![]() 20. They are strongly subject to interstellar
reddening. These indices suggest that SS 433 is a hot OB star with
the reddening
20. They are strongly subject to interstellar
reddening. These indices suggest that SS 433 is a hot OB star with
the reddening
![]() and the full extinction
and the full extinction
![]() of approximately 8
of approximately 8![]() (Murdin et al., 1980; Cherepashchuk
et al., 1982; Margon, 1984). Wagner (1986) found
(Murdin et al., 1980; Cherepashchuk
et al., 1982; Margon, 1984). Wagner (1986) found
![]() from continuum fitting of spectrophotometric observations
in the wavelength range between 4036 and 8100 Å. The mean color
temperature was about 32500 K, the continuum spectrum appeared
hotter when the precessing body was brighter, and these variations
corresponded to an amplitude of 0
from continuum fitting of spectrophotometric observations
in the wavelength range between 4036 and 8100 Å. The mean color
temperature was about 32500 K, the continuum spectrum appeared
hotter when the precessing body was brighter, and these variations
corresponded to an amplitude of 0![]() 08 in the
08 in the ![]() color.
color.
The most valuable information on jet structure and mass ratio of
the components of SS 433 can be derived from X-ray observations of
its eclipses. The Ginga X-ray observatory has made the most
important contribution to the research of SS 433. Three eclipses
were continuously monitored with a complete phase coverage at
different phases of the precession period, namely those in May
1987, May 1988 and May 1999; additional pointings to the object
were performed at different orbital and precession phases (Yuan et
al., 1995). It became clear that most X-rays were emitted from the
jets. The shape of the continuum could be fitted with a single
thermal bremsstrahlung model, its characteristic temperature
![]() being about 20 keV. With the eV-to-Kelvin reduction
coefficient of
being about 20 keV. With the eV-to-Kelvin reduction
coefficient of
![]() , this temperature is
, this temperature is
![]() K. Thus, there exists an uncovered source with a temperature
that high in the system. Note that one cannot distinguish thermal
sources with temperatures above
K. Thus, there exists an uncovered source with a temperature
that high in the system. Note that one cannot distinguish thermal
sources with temperatures above ![]() K using multicolor
K using multicolor ![]() photometry because their spectral energy distributions (SEDs) have
maxima far in the X-rays and their slopes are similar in the
photometry because their spectral energy distributions (SEDs) have
maxima far in the X-rays and their slopes are similar in the
![]() spectral region. Such energy distributions do not differ
much from those of an O-type star with a temperature about 32500 K
(Wagner, 1986), and their color temperature can be underestimated
due to the contribution from the red and infrared excess,
discovered with the help of the referee. Ginga observations also
show a strong K emission blend of Fe XXV/Fe XXVI at 6 keV that can
be extracted from the spectrum. The line shows the same
relativistic shifts as the moving "violet" (short-wavelength)
components of the Balmer emission. Some observations made near
spectral region. Such energy distributions do not differ
much from those of an O-type star with a temperature about 32500 K
(Wagner, 1986), and their color temperature can be underestimated
due to the contribution from the red and infrared excess,
discovered with the help of the referee. Ginga observations also
show a strong K emission blend of Fe XXV/Fe XXVI at 6 keV that can
be extracted from the spectrum. The line shows the same
relativistic shifts as the moving "violet" (short-wavelength)
components of the Balmer emission. Some observations made near
![]() and
and ![]() also display a moving "red" component from the
oppositely directed jet.
also display a moving "red" component from the
oppositely directed jet.
X-ray eclipses of SS 433 are partial and show strongly pronounced
contacts of the jet base with the companion's limb. One of the
eclipses registered by Ginga, centered at 1987 May ![]() UT (precession phase
UT (precession phase ![]() if counted from
if counted from ![]() ),
occurred in the high state (a strong flux and hard spectrum)
(Kawai et al., 1989; Brinkmann et al., 1989). The duration of the
eclipse measured as the time interval between contacts is 2
),
occurred in the high state (a strong flux and hard spectrum)
(Kawai et al., 1989; Brinkmann et al., 1989). The duration of the
eclipse measured as the time interval between contacts is 2![]() 4.
The shape of the eclipse is similar in different energy bands, the
intensity of the extracted K
4.
The shape of the eclipse is similar in different energy bands, the
intensity of the extracted K![]() line shows variations with
the same contacts and the same relative depth. This observation
confirms that it is the jet that is eclipsed, and the jet is the
brightest X-ray source in the system. Additionally, these
observations along with the well-known orbital inclination enable
us to measure the mass ratio of the components very accurately.
With the standard assumption that the optical star fills its Roche
lobe and using Paczynski's formula for the size of the Roche lobe,
line shows variations with
the same contacts and the same relative depth. This observation
confirms that it is the jet that is eclipsed, and the jet is the
brightest X-ray source in the system. Additionally, these
observations along with the well-known orbital inclination enable
us to measure the mass ratio of the components very accurately.
With the standard assumption that the optical star fills its Roche
lobe and using Paczynski's formula for the size of the Roche lobe,
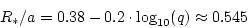 |
(2) |
Kawai et al. (1989) considered solutions for ![]() based on wider
assumptions like opposed jets, a thick accretion disk around the
compact object, a thick jet with a cylindrical axisymmetric shape.
These assumptions disperse the values of
based on wider
assumptions like opposed jets, a thick accretion disk around the
compact object, a thick jet with a cylindrical axisymmetric shape.
These assumptions disperse the values of ![]() in the 0.13-4.6
range. Different authors considered a cocoon instead of a jet, or
an eclipse of the jet by a star having an extended outflowing
envelope without any clear-cut limb. All these attempts were made
to increase
in the 0.13-4.6
range. Different authors considered a cocoon instead of a jet, or
an eclipse of the jet by a star having an extended outflowing
envelope without any clear-cut limb. All these attempts were made
to increase ![]() . In my opinion, a thin jet is a satisfactory
solution. Actually, no additional contacts are seen in the shape
of X-ray eclipses that would look like intensity jumps. In the
case of a thin jet, the exponential intensity decrease along its
length can be revealed from observations, it is described with the
following formula:
. In my opinion, a thin jet is a satisfactory
solution. Actually, no additional contacts are seen in the shape
of X-ray eclipses that would look like intensity jumps. In the
case of a thin jet, the exponential intensity decrease along its
length can be revealed from observations, it is described with the
following formula:
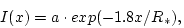 |
(3) |
ASCA high-resolution X-ray spectral observations performed on
April 23 and 24, 1993 resolved the K![]() blend at 6 keV into
Fe XXV and Fe XXVI lines; each line showed both a strong
"violet" component and a faint "red" one (Kotani et al.,
1994). Both components had large Doppler shifts, and positions of
components in the spectra agreed with the kinematical model.
Detections of moving lines of Ar XVII, Ar XVIII, S XV, S XVI,
Ca XIX, and Ni XXVII ions were also reported. XMM observations
(Brinkmann et al., 2005) also confirm large Doppler-shifted
emission components; the "red" jet contributes 30-40 percents
to the total photon flux. The best estimates of the temperature at
the jet base are around
blend at 6 keV into
Fe XXV and Fe XXVI lines; each line showed both a strong
"violet" component and a faint "red" one (Kotani et al.,
1994). Both components had large Doppler shifts, and positions of
components in the spectra agreed with the kinematical model.
Detections of moving lines of Ar XVII, Ar XVIII, S XV, S XVI,
Ca XIX, and Ni XXVII ions were also reported. XMM observations
(Brinkmann et al., 2005) also confirm large Doppler-shifted
emission components; the "red" jet contributes 30-40 percents
to the total photon flux. The best estimates of the temperature at
the jet base are around
![]() keV. The "stationary
line" in K
keV. The "stationary
line" in K![]() around 7 keV was found in the Ginga data, but
not in later ASCA and Chandra observations (Brinkmann et al.,
2005). The XMM K
around 7 keV was found in the Ginga data, but
not in later ASCA and Chandra observations (Brinkmann et al.,
2005). The XMM K![]() line profiles seem to be strongly
affected by the "stationary line", which may be an indicator of
Compton scattering of jet base radiation on surrounding cold
matter. One eclipse, dated 2003 May 11, was observed by the
INTEGRAL X-ray observatory in hard X-rays ranged between 25 and
100 keV during a large campaign including optical spectroscopy,
optical and infrared photometry (Cherepashchuk et al., 2005).
Unfortunately, the phase coverage of the eclipse in hard rays was
insufficient. Nevertheless, fragments of light curves suggest that
the width of the hard X-ray eclipse is larger than in soft X-rays;
probably the width increases with energy. The hard X-ray eclipse
is at least two times deeper than the soft X-ray eclipse. No
contacts were seen. Thus, the authors treat the eclipse as an
occultation not of a jet but of a "corona" surrounding the
accretion disk.
line profiles seem to be strongly
affected by the "stationary line", which may be an indicator of
Compton scattering of jet base radiation on surrounding cold
matter. One eclipse, dated 2003 May 11, was observed by the
INTEGRAL X-ray observatory in hard X-rays ranged between 25 and
100 keV during a large campaign including optical spectroscopy,
optical and infrared photometry (Cherepashchuk et al., 2005).
Unfortunately, the phase coverage of the eclipse in hard rays was
insufficient. Nevertheless, fragments of light curves suggest that
the width of the hard X-ray eclipse is larger than in soft X-rays;
probably the width increases with energy. The hard X-ray eclipse
is at least two times deeper than the soft X-ray eclipse. No
contacts were seen. Thus, the authors treat the eclipse as an
occultation not of a jet but of a "corona" surrounding the
accretion disk.
Finally, weak lines of an A-type star, a probable mass donor were
discovered during eclipses in the spectra of SS 433 (Gies et al.,
2002a). These lines are present in the blue spectral range. The
lines of the A star are weak, its spectroscopic contribution in
the mid-eclipse is estimated as ![]() in the
in the ![]() band
(Hillwig & Gies, 2008). After this discovery, several attempts
were made to determine masses of SS 433 components with the
dynamic method, i.e. measuring amplitudes of the radial velocity
curves,
band
(Hillwig & Gies, 2008). After this discovery, several attempts
were made to determine masses of SS 433 components with the
dynamic method, i.e. measuring amplitudes of the radial velocity
curves, ![]() and
and ![]() . The results are reviewed in Kubota et
al. (2010). They are the following.
. The results are reviewed in Kubota et
al. (2010). They are the following.
| Source | |||
| Gies et al. (2002a) | 0.58 | ||
| Gies et al. (2002b) | 0.72 | ||
| Hillwig et al. (2004) | 10.9 |
0.27 | |
| Cherepashchuk et al. (2005) | 18 | 24 | 0.75 |
| Hillwig & Gies (2008) | 0.35 | ||
| Kubota et al. (2010) |
|
However, Barnes et al. (2006) argued that the A-type supergiant spectrum may not be formed in the photosphere of the donor, it probably originates in the accretion disk wind. In such a case, the visibility of absorption lines should decrease in eclipse, but the reverse effect is observed. This is a good reason to believe that an A-type donor exists in the system.
Whatever the source, the donor or the wind, the data ambiguity
concerning the components' masses reflects difficulties of the
dynamic method. These difficulties are the following. With ![]() as
small as 0.15 and with a very hot radiation source heating the
surface of the A-type star, we can observe the absorption-line
spectrum only from the opposite side of the donor. The mass center
of the system is located near the center of the donor, so actually
we see the effect of donor's synchronous rotation, not the orbital
motion. This effect leads to an overestimate of the amplitude of
mass-center motion. Kubota et al. (2010) tried to account for this
effect, and the lower limit of the mass estimate decreased to
as
small as 0.15 and with a very hot radiation source heating the
surface of the A-type star, we can observe the absorption-line
spectrum only from the opposite side of the donor. The mass center
of the system is located near the center of the donor, so actually
we see the effect of donor's synchronous rotation, not the orbital
motion. This effect leads to an overestimate of the amplitude of
mass-center motion. Kubota et al. (2010) tried to account for this
effect, and the lower limit of the mass estimate decreased to ![]() as a result. With a simple model, they reduced
as a result. With a simple model, they reduced ![]() to
to ![]() km s
km s![]() . They conclude that "the compact object
in SS 433 is most likely a low mass black hole, although the
possibility of a massive neutron star cannot be firmly excluded".
Otherwise, the mass of a neutron star may be close to the
Chandrasekhar limit of
. They conclude that "the compact object
in SS 433 is most likely a low mass black hole, although the
possibility of a massive neutron star cannot be firmly excluded".
Otherwise, the mass of a neutron star may be close to the
Chandrasekhar limit of ![]() if SS 433 is a semidetached
system with a heavy accretion disk (having a mass of
if SS 433 is a semidetached
system with a heavy accretion disk (having a mass of ![]() ), or, what is more probable, a contact system with an
), or, what is more probable, a contact system with an
![]() star-like component having a neutron core (the
Thorne & Zhitkov (1975, 1977) case). Certainly, one should take
into account the presence of other matter in addition to the
compact star in its Roche lobe in the system with a large rate of
mass exchange.
star-like component having a neutron core (the
Thorne & Zhitkov (1975, 1977) case). Certainly, one should take
into account the presence of other matter in addition to the
compact star in its Roche lobe in the system with a large rate of
mass exchange.
Additionally, most authors used ![]() km s
km s![]() , as
measured by Fabrika & Bychkova (1990) on the base of the HeII
4686 Å line or
, as
measured by Fabrika & Bychkova (1990) on the base of the HeII
4686 Å line or ![]() km s
km s![]() from Gies et al.
(2002b), based on the CII 7231, 7236 Å blend. These emissions
were attributed by the cited authors to the accretion disk
surrounding the compact companion. This is a weak assumption.
Typically, the HeII line has
from Gies et al.
(2002b), based on the CII 7231, 7236 Å blend. These emissions
were attributed by the cited authors to the accretion disk
surrounding the compact companion. This is a weak assumption.
Typically, the HeII line has
![]() km s
km s![]() , with
wings to
, with
wings to
![]() km s
km s![]() . In an eclipse, the
equivalent width increases due to fainter continuum, so the
largest part of the emission belongs to a nebular envelope
surrounding the system but not to the accretion disk. Indeed, its
shape is sometimes double-peaked. However, in an eclipse, we
should expect, first, covering the blue peak from the approaching
disk stream; then, covering the red peak from the recessing
stream; and then, their consequent recovering. Actually, the
eclipse in HeII line goes otherwise. The blue wing of the line is
eclipsed, and the line becomes narrower, what Goranskij et al.
(1997) treat as an eclipse of a wide-angle conical outflow
directed along the jet. Our analysis of the spectra by Kubota et
al. (2010) taken in the eclipse on 2007 October 6 confirms this
behavior of the HeII line. Thus, problems of dynamic mass
determination for SS 433 are due to complex structure of lines
that do not reflect the mass-center motion of the components.
. In an eclipse, the
equivalent width increases due to fainter continuum, so the
largest part of the emission belongs to a nebular envelope
surrounding the system but not to the accretion disk. Indeed, its
shape is sometimes double-peaked. However, in an eclipse, we
should expect, first, covering the blue peak from the approaching
disk stream; then, covering the red peak from the recessing
stream; and then, their consequent recovering. Actually, the
eclipse in HeII line goes otherwise. The blue wing of the line is
eclipsed, and the line becomes narrower, what Goranskij et al.
(1997) treat as an eclipse of a wide-angle conical outflow
directed along the jet. Our analysis of the spectra by Kubota et
al. (2010) taken in the eclipse on 2007 October 6 confirms this
behavior of the HeII line. Thus, problems of dynamic mass
determination for SS 433 are due to complex structure of lines
that do not reflect the mass-center motion of the components.
Alternatively, we can find masses of the components in the system
of SS 433 from the spectroscopic contribution of the A-type donor
during an eclipse (![]() % in the
% in the ![]() band). For the known
upper limits of distance (
band). For the known
upper limits of distance (![]() pc) and interstellar
extinction (
pc) and interstellar
extinction (
![]() ), we can calculate the lower limit of
the donor's absolute magnitude,
), we can calculate the lower limit of
the donor's absolute magnitude,
![]() , from a simple
formula:
, from a simple
formula:
 |
(4) |
Nevertheless, I tried to verify and improve the modern data on mass ratio, interstellar extinction, photometric calibration using contemporary optical and X-ray observations. It is also of interest to estimate the contribution from the A-type donor using the photometric method.
2. ORBITAL PERIOD AND MASS RATIO
To check the mass ratio determined with the GINGA X-ray
observatory, I used 79784 X-ray observations of RXTE/ASM in the
![]() keV energy range accumulated between 1996 January 5 and
2011 March 9 at the RXTE Internet site:
keV energy range accumulated between 1996 January 5 and
2011 March 9 at the RXTE Internet site:
http://xte.mit.edu/ASM_lc.html.These observations have a very low accuracy, but with the number of measurements that large, if averaged in orbital or precession phase bins, they allow us to establish the shapes of precession and eclipse light curves in this energy range. The orbital period was improved using our collection of photometric
http://jet.sao.ru/~goray/v1343aql.htm.The table of observations is accessible in the file:
http://jet.sao.ru/~goray/SS.DAT.The first column of the Table contains Julian Dates of observations in the form of
The 35 best revised and new mid-eclipse times are given in Table 1. To determine these times, the eclipse light curves were superposed with the same, but mirrored, curves in the PC screen; the axis of the mirror reflection was taken for the center of an eclipse. With these eclipse timings, the light ephemeris was determined using least squares fitting, with the following result:
|
(5) |
The O![]() C curve calculated with this ephemeris is shown
in Fig. 3 (top). Note that the deviations of individual minima
from the ephemeris are larger than their mean errors. Figure 3
(bottom) demonstrates that these deviations do not depend on the
precession phase. Precession phases
C curve calculated with this ephemeris is shown
in Fig. 3 (top). Note that the deviations of individual minima
from the ephemeris are larger than their mean errors. Figure 3
(bottom) demonstrates that these deviations do not depend on the
precession phase. Precession phases ![]() were calculated using
the following ephemeris:
were calculated using
the following ephemeris:
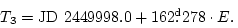 |
(6) |
Fitting the O![]() C curve with a quadratic expression reveals the
quadratic term to be insignificant. This means that the orbital
period did not vary between 1979 and 2007.
C curve with a quadratic expression reveals the
quadratic term to be insignificant. This means that the orbital
period did not vary between 1979 and 2007.
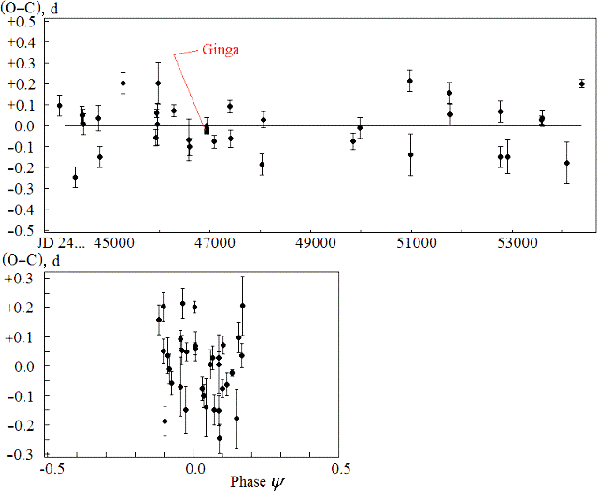 |
Fig. 3.
The O |
The light curve for RXTE/ASM data in the ![]() keV energy range
plotted versus phases
keV energy range
plotted versus phases ![]() of the orbital period calculated from
eq. (5) is shown in Fig. 4 (top). The points deviating from zero
by more than
of the orbital period calculated from
eq. (5) is shown in Fig. 4 (top). The points deviating from zero
by more than ![]() cts s
cts s![]() were eliminated. Figure 4
(middle) demonstrates the same data plotted versus phases
were eliminated. Figure 4
(middle) demonstrates the same data plotted versus phases ![]() of the precession period calculated with the formula (6). This is
a mean light curve averaged by phase using the moving-average
method, with a phase interval of 0.10. The curve indicates
periodic variability of the X-ray flux in the range between 0.15
and 0.55 cts s
of the precession period calculated with the formula (6). This is
a mean light curve averaged by phase using the moving-average
method, with a phase interval of 0.10. The curve indicates
periodic variability of the X-ray flux in the range between 0.15
and 0.55 cts s![]() , i.e. by the factor of 3.7. Figure 4
(bottom) demonstrates the residuals revealed by prewhitening the
data for the precession wave, plotted versus the orbital-period
phase again. The residuals were averaged by phase
, i.e. by the factor of 3.7. Figure 4
(bottom) demonstrates the residuals revealed by prewhitening the
data for the precession wave, plotted versus the orbital-period
phase again. The residuals were averaged by phase ![]() calculated from eq. (5) using the same moving-average method but
with a smaller phase interval of 0.05. The mean orbital light
curve shows the average flux constant in the phase range between
0.10 and 0.90, with a dip at phases between 0.90 and 0.10 due to
the eclipse. The RXTE/ASM light curve is compared to the GINGA
light curve for the eclipse on 1987 May 20 in Fig. 5. Taking into
account a small systematic shift of the individual eclipse
relative to averaged curve of multiple eclipses and smoothing the
averaged curve with the width of average interval, one finds the
agreement to be good enough. The RXTE/ASM data confirm that the
eclipse is caused by covering the jet base, and the jet base is
located as close to the donor's surface as follows from the mass
ratio of
calculated from eq. (5) using the same moving-average method but
with a smaller phase interval of 0.05. The mean orbital light
curve shows the average flux constant in the phase range between
0.10 and 0.90, with a dip at phases between 0.90 and 0.10 due to
the eclipse. The RXTE/ASM light curve is compared to the GINGA
light curve for the eclipse on 1987 May 20 in Fig. 5. Taking into
account a small systematic shift of the individual eclipse
relative to averaged curve of multiple eclipses and smoothing the
averaged curve with the width of average interval, one finds the
agreement to be good enough. The RXTE/ASM data confirm that the
eclipse is caused by covering the jet base, and the jet base is
located as close to the donor's surface as follows from the mass
ratio of ![]() = 0.15.
= 0.15.
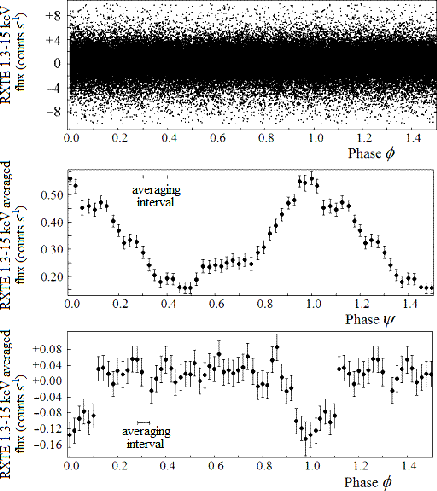 |
Fig. 4.
The RXTE/ASM X-ray phased light
curves. Top: 79784 X-ray observations plotted versus the phase of
the orbital 13.08223-day period. Middle: the averaged light curve
calculated with the precession period of 162 |
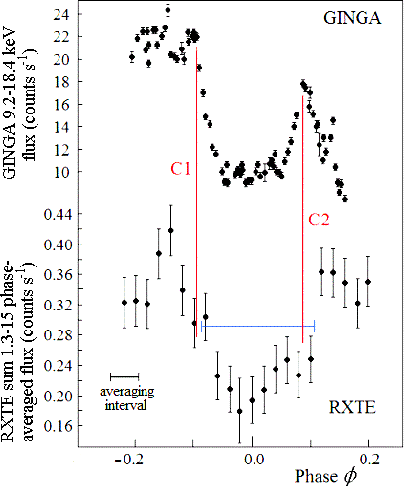 |
Fig. 5.
Comparison of X-ray eclipse light
curve shapes. Top: the GINGA light curve for the eclipse on 1987
May 20. Bottom: the average eclipse light curve from RXTE/ASM
data. |
3. THE INTERSTELLAR EXTINCTION LAW
SS 433 is subject to strong extinction by interstellar medium.
This extinction is a sum of absorption and scattering of the star
light by the interstellar dust; physics of these processes is
described by Savage & Mathys (1979). The ![]() -band extinction of
SS 433 light may reach 8 magnitudes. To estimate the absolute
magnitude of the A-type donor of SS 433, we need to know both the
accurate reddening
-band extinction of
SS 433 light may reach 8 magnitudes. To estimate the absolute
magnitude of the A-type donor of SS 433, we need to know both the
accurate reddening ![]() and the shape of the
interstellar-extinction curve,
and the shape of the
interstellar-extinction curve, ![]() , normalized to unit
reddening,
, normalized to unit
reddening, ![]() = 1.0. The extinction curve was a subject of
many studies; cf. the historical review in Straizys (1977). It was
ascertained that the shape of the extinction curve varied in
different directions and had different anomalies both in the
near-ultraviolet and near-infrared ranges. Strong anomalies were
found in the ultraviolet range in the nearby LMC and SMC galaxies.
In Fig. 6, we compare the interstellar extinction law curves
measured by J. Sudzius (published in Straizys, 1977) for the
directions of Cepheus, Perseus, and Monoceros (converted from
optical depths to magnitudes) to later-published curves by Schild
(1977), Savage & Mathys (1979), Seaton (1979), Koorneef & Code
(1981), Nandy et al. (1981), Howarth (1983), and Prevot et al.
(1984). Most authors agree that
= 1.0. The extinction curve was a subject of
many studies; cf. the historical review in Straizys (1977). It was
ascertained that the shape of the extinction curve varied in
different directions and had different anomalies both in the
near-ultraviolet and near-infrared ranges. Strong anomalies were
found in the ultraviolet range in the nearby LMC and SMC galaxies.
In Fig. 6, we compare the interstellar extinction law curves
measured by J. Sudzius (published in Straizys, 1977) for the
directions of Cepheus, Perseus, and Monoceros (converted from
optical depths to magnitudes) to later-published curves by Schild
(1977), Savage & Mathys (1979), Seaton (1979), Koorneef & Code
(1981), Nandy et al. (1981), Howarth (1983), and Prevot et al.
(1984). Most authors agree that ![]() at
at
![]() ,
but this value may be somewhat variable.
,
but this value may be somewhat variable.
The formula to calculate interstellar extinction ![]() is:
is:
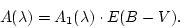 |
(7) |
Observations show some deviations in the ![]() -band extinction law
that can reach 0
-band extinction law
that can reach 0![]() 8. The largest deviation downward found in the
ultraviolet is exhibited by the extinction curves in the LMC and
SMC by Nandy et al. (1989), curve 5; Koornneef & Code (1981),
curve 6; and Howarth (1983), curve 8a. Curve 8 by Howarth (1983),
measured for the Galaxy, does not show a deviation that big. The
largest deviation downward for the Galaxy is in the curve 6 by
Schild (1977). This author found anomalous absorption below the
Balmer jump in Perseus and in one region in Cygnus, but the normal
law in the other Cygnus region. According to Galactic data, the
dispersion of extinction curves in the UV band in our Galaxy may
reach 0
8. The largest deviation downward found in the
ultraviolet is exhibited by the extinction curves in the LMC and
SMC by Nandy et al. (1989), curve 5; Koornneef & Code (1981),
curve 6; and Howarth (1983), curve 8a. Curve 8 by Howarth (1983),
measured for the Galaxy, does not show a deviation that big. The
largest deviation downward for the Galaxy is in the curve 6 by
Schild (1977). This author found anomalous absorption below the
Balmer jump in Perseus and in one region in Cygnus, but the normal
law in the other Cygnus region. According to Galactic data, the
dispersion of extinction curves in the UV band in our Galaxy may
reach 0![]() 5.
5.
I have chosen the Savage & Mathys (1979) curve as a template to
use for SS 433 because it is in the best agreement with other
observations in the ![]() spectral range and is frequently used in
data reductions with the ESO MIDAS package. It should be taken
into account that this table of extinction can have an
insufficient accuracy when applied to reductions for a star as
absorbed as SS 433.
spectral range and is frequently used in
data reductions with the ESO MIDAS package. It should be taken
into account that this table of extinction can have an
insufficient accuracy when applied to reductions for a star as
absorbed as SS 433.
Fortunately, there is a method to correct the individual
extinction law for SS 433 on the base of multicolor photometry or
spectrophotometry. Using observations of SS 433 during an eclipse,
we can extract the spectrum of the very hot central source, which
is covered in eclipses, from the combined light of the system. The
combined light contains also the radiation from the surrounding
gaseous shell and disk. We assume that the extracted spectrum is
an extension of the thermal bremsstrahlung continuum that is
radiated by the jet, its temperature being about ![]() K
(Yuan et al., 1995). The slope of such a spectrum in the wide
wavelength range covering near-UV, optical, and near-IR domains is
similar for temperatures exceeding
K
(Yuan et al., 1995). The slope of such a spectrum in the wide
wavelength range covering near-UV, optical, and near-IR domains is
similar for temperatures exceeding ![]() K. The extracted
continuum can be used as a calibration standard to measure the
extinction. The problem of extinction can be solved by comparison
of the observed extracted spectral energy distribution to a
calculated energy distribution for a black body with
K. The extracted
continuum can be used as a calibration standard to measure the
extinction. The problem of extinction can be solved by comparison
of the observed extracted spectral energy distribution to a
calculated energy distribution for a black body with
![]() K.
K.
 |
Fig. 6. Curves of the interstellar extinction law measured in different studies. 1: Sudzius (Straizys, 1977); 2: Schild (1977); 3: Savage & Mathis (1979); 4: Prevot et al. (1984) for the SMC; 5: Nandy et al. (1989) for the LMC; 6: Koornneef & Code (1981) for the LMC, from observations with the IUE observatory; 7: Seaton (1979); 8: Howarth (1983) for the Galaxy; 8a: Howarth (1983) for the LMC. The extinction curve by Savage & Mathis (1979) (No. 3), plotted red, was chosen for this study. |
4. OBSERVATIONS AND DATA REDUCTION
To analyze spectral energy distributions, I used multicolor CCD
![]() photometry of SS 433 in two eclipses centered at 2003
October 1 (JD 2452914.77;
photometry of SS 433 in two eclipses centered at 2003
October 1 (JD 2452914.77; ![]() ) and 2007 October 6 (JD
2454380.33;
) and 2007 October 6 (JD
2454380.33; ![]() ) from our collection mentioned in
Section 2. The observations were made with the SAO 1-m Zeiss
reflector and a photometer equipped with an EEV 42-40 chip and
standard filters. Observations of the eclipse on 2007 October 6
were a part of a big campaign and accompanied with extensive
spectroscopy using the Russian 6-m BTA telescope and the Japanese
8-meter Subaru telescope. The results of this campaign were
published by Kubota et al. (2010). During spectroscopic
observations with the Subaru telescope, a series of direct CCD
frames with the
) from our collection mentioned in
Section 2. The observations were made with the SAO 1-m Zeiss
reflector and a photometer equipped with an EEV 42-40 chip and
standard filters. Observations of the eclipse on 2007 October 6
were a part of a big campaign and accompanied with extensive
spectroscopy using the Russian 6-m BTA telescope and the Japanese
8-meter Subaru telescope. The results of this campaign were
published by Kubota et al. (2010). During spectroscopic
observations with the Subaru telescope, a series of direct CCD
frames with the ![]() filter were acquired in order to point the
star into the spectrograph slit. I reduced these frames and also
used them for the analysis. Additionally, I used the BTA and
Subaru spectroscopy to estimate the emission-line contribution in
the photometric bands. The Subaru/FOCAS spectra are from four
nights between 2007 October 6 and 10 and cover the wavelength
range of
filter were acquired in order to point the
star into the spectrograph slit. I reduced these frames and also
used them for the analysis. Additionally, I used the BTA and
Subaru spectroscopy to estimate the emission-line contribution in
the photometric bands. The Subaru/FOCAS spectra are from four
nights between 2007 October 6 and 10 and cover the wavelength
range of ![]() Å with a dispersion of 0.37 Å per
pixel. The BTA/SCORPIO spectra were taken on four nights between
2007 October 4 and 7 and cover the
Å with a dispersion of 0.37 Å per
pixel. The BTA/SCORPIO spectra were taken on four nights between
2007 October 4 and 7 and cover the ![]() Å range with a
dispersion of 0.86 Å per pixel.
Å range with a
dispersion of 0.86 Å per pixel.
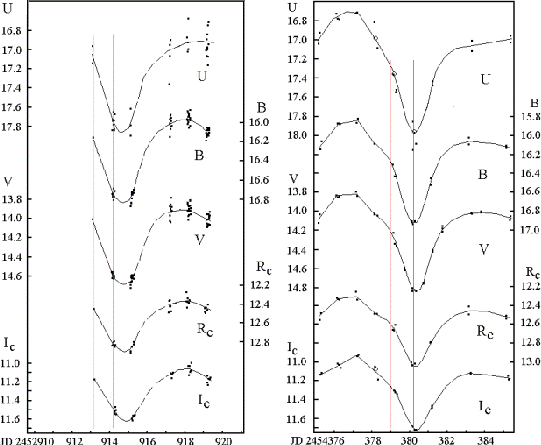 |
Fig. 7.
The light curves of two eclipses,
on 2003 October 1 (left) and on 2007 October 6 (right), in the
|
The CCD photometry was reduced in a standard way using bias and
flat field frames. Dark frames were not applied because of deep
freezing of the CCD chip with liquid nitrogen to a temperature of
![]() C. The thermal noise is negligible at this temperature.
The nearby star Lyuty 9 (GSC 00471-00142), the southern star of
the rhomb, was the comparison star. The star has a faint red
companion at 6
C. The thermal noise is negligible at this temperature.
The nearby star Lyuty 9 (GSC 00471-00142), the southern star of
the rhomb, was the comparison star. The star has a faint red
companion at 6
![]() 0 NE; its contribution to the combined light
is significant in the
0 NE; its contribution to the combined light
is significant in the ![]() ,
, ![]() , and
, and ![]() bands in the cases of poor
seeing. On such occasions, the comparison-star pixels affected
with the companion were eliminated from the star profile, and
their intensities were replaced with average-profile intensities
when computing the integrated light. Extraction of images was
performed with my software WinFITS in the aperture mode, with a
star-profile correction. The
bands in the cases of poor
seeing. On such occasions, the comparison-star pixels affected
with the companion were eliminated from the star profile, and
their intensities were replaced with average-profile intensities
when computing the integrated light. Extraction of images was
performed with my software WinFITS in the aperture mode, with a
star-profile correction. The ![]() magnitudes of the
comparison star are respectively the following: 15.073, 14.581,
13.431, 12.973, 12.383. Additionally, four check stars were used.
The uncertainty of the measurements is about
magnitudes of the
comparison star are respectively the following: 15.073, 14.581,
13.431, 12.973, 12.383. Additionally, four check stars were used.
The uncertainty of the measurements is about
![]() in
the
in
the ![]() filters, and about 0
filters, and about 0![]() 1 in the
1 in the ![]() filter.
Generally, several observations were done on a night. The light
curves of the two above-mentioned eclipses are shown in Fig. 7 for
all the filters. In a few cases when nightly differences of
measured magnitudes were sufficiently large, I co-added frames
with matchimg star images and remeasured the nightly-sum frame.
Such observations are marked with circles in the Figure.
filter.
Generally, several observations were done on a night. The light
curves of the two above-mentioned eclipses are shown in Fig. 7 for
all the filters. In a few cases when nightly differences of
measured magnitudes were sufficiently large, I co-added frames
with matchimg star images and remeasured the nightly-sum frame.
Such observations are marked with circles in the Figure.
As follows from the X-ray observations (Fig. 5), the ingress of
the jet base begins at
![]() , the egress ends at
, the egress ends at
![]() and the eclipse of the jet is partial. Near
the jet base ingress, the optical light decline is most rapid. To
extract the spectral energy distribution of the hot light source
using the difference method, we should include phases
and the eclipse of the jet is partial. Near
the jet base ingress, the optical light decline is most rapid. To
extract the spectral energy distribution of the hot light source
using the difference method, we should include phases ![]() of both eclipses in the phase interval where the light loss
of the hot source happens. These intervals are shown in Fig. 7
with vertical lines. In the eclipse on 2007 October 6, both
ingress and egress were observed. The shape of the eclipse was
symmetric, the light curve is well compatible with its reflected
one. Therefore, I used both egress and ingress to measure the
light lost in the eclipse. I interpolated magnitudes to include
phases of the jet base contact. To compare the energy distribution
of the light lost in the eclipse to the Planck energy
distribution, we should transform magnitudes into physical units
of erg cm
of both eclipses in the phase interval where the light loss
of the hot source happens. These intervals are shown in Fig. 7
with vertical lines. In the eclipse on 2007 October 6, both
ingress and egress were observed. The shape of the eclipse was
symmetric, the light curve is well compatible with its reflected
one. Therefore, I used both egress and ingress to measure the
light lost in the eclipse. I interpolated magnitudes to include
phases of the jet base contact. To compare the energy distribution
of the light lost in the eclipse to the Planck energy
distribution, we should transform magnitudes into physical units
of erg cm![]() s
s![]() Å
Å![]() .
.
5. ABSOLUTE CALIBRATION OF THE  SYSTEM
SYSTEM
It is known that the zero point of the ![]() photometric
system is related to A0V stars. It is accepted by definition that
all unreddened color indices of such star are zeros.
Spectrophotometry deals with monochromatic intensities, i.e.
intensities are measured in the physical units, and an element of
spectral dispersion (pixel) is so small that intensity varies
insignificantly between nearby elements. In the wide-band
photometry, the width of transmission curve is usually thousands
of Angströms, and stellar magnitudes are heterochromatic. In the
spectral energy distribution measured with wide-band photometry,
each magnitude corresponds to the mean wavelength of the device
transmission curve
photometric
system is related to A0V stars. It is accepted by definition that
all unreddened color indices of such star are zeros.
Spectrophotometry deals with monochromatic intensities, i.e.
intensities are measured in the physical units, and an element of
spectral dispersion (pixel) is so small that intensity varies
insignificantly between nearby elements. In the wide-band
photometry, the width of transmission curve is usually thousands
of Angströms, and stellar magnitudes are heterochromatic. In the
spectral energy distribution measured with wide-band photometry,
each magnitude corresponds to the mean wavelength of the device
transmission curve ![]() , calculated as:
, calculated as:
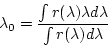 |
(8) |
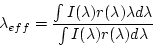 |
(9) |
Straizys (1977) used the calibration of ![]() magnitudes from
Straizys & Kuriliene (1975), based on the Vilnius photoelectric
system. These calibration flux densities for a zero-magnitude A0V
star are given in the fourth column of Table 2. The mean
wavelengths
magnitudes from
Straizys & Kuriliene (1975), based on the Vilnius photoelectric
system. These calibration flux densities for a zero-magnitude A0V
star are given in the fourth column of Table 2. The mean
wavelengths ![]() for the filters given in column 2 of this
Table were calculated by me via eq. (8) using filter transmission
curves presented in the digital form by Moro & Munari (2000).
Moro & Munari give Vilnius coefficients along with another
version of coefficients, which became popular and are called the
photoelectric USA version (Matthews & Sandage, 1963). These
for the filters given in column 2 of this
Table were calculated by me via eq. (8) using filter transmission
curves presented in the digital form by Moro & Munari (2000).
Moro & Munari give Vilnius coefficients along with another
version of coefficients, which became popular and are called the
photoelectric USA version (Matthews & Sandage, 1963). These ![]() data along with the Cousins
data along with the Cousins ![]() calibration coefficients are
given in Column 5 of Table 2. Note that the reduction coefficients
of the Vilnius and USA systems differ by 5.7 percents in the
calibration coefficients are
given in Column 5 of Table 2. Note that the reduction coefficients
of the Vilnius and USA systems differ by 5.7 percents in the
![]() band and by 8.6 percents in the
band and by 8.6 percents in the ![]() band, just in the spectral
region where the strong multiple Balmer absorptions of an A0V star
and its Balmer jump are located. Such a big uncertainty is
inadmissible for SS 433 calibration.
band, just in the spectral
region where the strong multiple Balmer absorptions of an A0V star
and its Balmer jump are located. Such a big uncertainty is
inadmissible for SS 433 calibration.
Therefore, I examined the reduction coefficients of the
![]() system using Moro & Munari transmission curves with
the modern spectral energy distribution of the A0V star Vega
published by Bohlin & Gilliland (2004). The
system using Moro & Munari transmission curves with
the modern spectral energy distribution of the A0V star Vega
published by Bohlin & Gilliland (2004). The ![]() magnitude of
magnitude of
![]() is established for Vega in the cited paper, and
the absolute flux level is
is established for Vega in the cited paper, and
the absolute flux level is
![]() erg cm
erg cm![]() s
s![]() at
at ![]() Å. The reduction
coefficients were calculated as average values of the Vega flux
density weighted with the filter transmission curve, as follows
from the formula:
Å. The reduction
coefficients were calculated as average values of the Vega flux
density weighted with the filter transmission curve, as follows
from the formula:
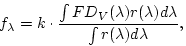 |
(10) |
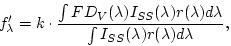 |
(11) |
 |
Fig. 8.
The spectral energy distributions
of SS 433 in two eclipses, on 2003 October 1 (a) and on 2007
October 6 (b), not corrected for interstellar extinction. 1: The
near-contact distribution, jet base included; 2: the distribution
near the eclipse center, jet base covered; 3: the energy
distribution in the |
The results are given in Table 3, where the effective wavelengths of measured light are given in Column 2, their logarithms are in Column 3, and the "A0V-star zero-magnitude" reduction coefficients for these effective wavelengths are in Column 4. Comparison of Columns 2 in Tables 2 and 3 shows that the effective wavelengths in the short-wavelength filters differ from the mean wavelengths by about 200 Å, and this effect should be taken into account for SS 433.
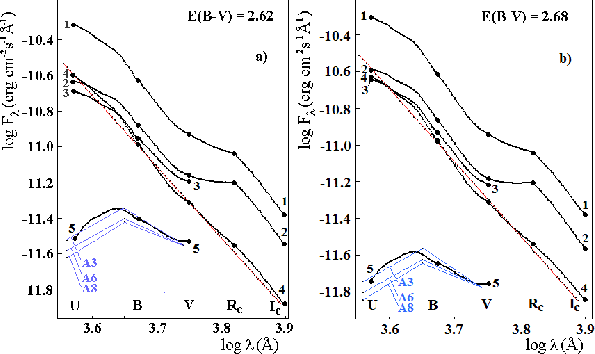 |
Fig. 9.
The spectral energy distributions
of SS 433 in two eclipses, on 2003 October 1 (a) and on 2007
October 6 (b), corrected for interstellar extinction. Numbers |
The spectral energy distributions of SS 433 in the two eclipses,
after such a correction but not yet corrected for interstellar
extinction, are shown in Fig. 8. The results of
energy-distribution correction for interstellar extinction made
individually for both eclipses are shown in Fig. 9. In Figs. 8 and
9, different energy distributions are plotted, those of light near
the jet-base contact with the jet base included, those of light
near the eclipse center with the jet base covered in the eclipse,
and those of light lost in the eclipse. The distribution of the
lost light is calculated as the difference of distributions with
the jet base included and excluded. The correction for
interstellar extinction was made by choosing a color excess value
to get the best fitting, by eye, of the lost-light distribution
(No. 3) with the black-body distribution for ![]() K (the
straight red line in Fig. 9). In such fitting, the level of
black-body distribution was a free parameter, so a color excess
was chosen only to fit its slope. With the photometry of 2003
October 1 eclipse, the best-fit color excess is 2
K (the
straight red line in Fig. 9). In such fitting, the level of
black-body distribution was a free parameter, so a color excess
was chosen only to fit its slope. With the photometry of 2003
October 1 eclipse, the best-fit color excess is 2![]() 62, and for
2007 October 6 eclipse, it is 2
62, and for
2007 October 6 eclipse, it is 2![]() 68. The average is
68. The average is
![]() .
.
It is important to note that the strong excess in the ![]() and
and ![]() bands described above is revealed in every energy distribution of
SS 433 being compared to the distribution of light lost in the
eclipse. It is seen both in Fig. 8 in the reddened data and in
Fig. 9 in unreddened data. The contribution of this excess can be
easily extracted from the combined light. For this purpose, we
extrapolate linearly the short-wavelength part of the
combined-light distribution to the
bands described above is revealed in every energy distribution of
SS 433 being compared to the distribution of light lost in the
eclipse. It is seen both in Fig. 8 in the reddened data and in
Fig. 9 in unreddened data. The contribution of this excess can be
easily extracted from the combined light. For this purpose, we
extrapolate linearly the short-wavelength part of the
combined-light distribution to the ![]() and
and ![]() bands and subtract
the extrapolated values. However, the excess veils such a faint
light source as an A-type star and makes its extraction impossible
in the
bands and subtract
the extrapolated values. However, the excess veils such a faint
light source as an A-type star and makes its extraction impossible
in the ![]() and
and ![]() bands.
bands.
The shape of the lost-light energy distribution, corrected for
reddening with the determined ![]() , is nearly a straight
line. This fact confirms my assumption on the nature of this
light source as an optical tail of the energy distribution
radiated by the jet bases. The maximum of this energy distribution
is located far in X-rays. The individual points of the lost-light
distribution indicate small deviations from the straight line in
different filters (Fig. 9a,b), probably due to systematic errors
in comparison-star magnitudes, uncertainties of the chosen
extinction law, or inconsistency of the general law with the
individual law in the particular sky direction, etc. Thus, the
individual extinction law can be derived as the difference between
the observed lost-light energy distribution and the selected
calculated Planck energy distribution divided by the average of
reddening.
, is nearly a straight
line. This fact confirms my assumption on the nature of this
light source as an optical tail of the energy distribution
radiated by the jet bases. The maximum of this energy distribution
is located far in X-rays. The individual points of the lost-light
distribution indicate small deviations from the straight line in
different filters (Fig. 9a,b), probably due to systematic errors
in comparison-star magnitudes, uncertainties of the chosen
extinction law, or inconsistency of the general law with the
individual law in the particular sky direction, etc. Thus, the
individual extinction law can be derived as the difference between
the observed lost-light energy distribution and the selected
calculated Planck energy distribution divided by the average of
reddening.
If we adopt the light contribution of an A4-A8 donor between 0.29
and 0.43 in the eclipse in the ![]() filter (Hillwig & Gies, 2008),
and taking into account the earlier described parameters and
uncertainties of distance and extinction, the absolute magnitude
of the donor will be limited to
filter (Hillwig & Gies, 2008),
and taking into account the earlier described parameters and
uncertainties of distance and extinction, the absolute magnitude
of the donor will be limited to
![]() .
In the spectral type - absolute magnitude diagram (Fig. 10), the
star occupies the uncertainty region plotted as a green rectangle.
The radius of such a star can be calculated using the
Stephan-Boltzmann law,
.
In the spectral type - absolute magnitude diagram (Fig. 10), the
star occupies the uncertainty region plotted as a green rectangle.
The radius of such a star can be calculated using the
Stephan-Boltzmann law,
![]() , or, in solar
units,
, or, in solar
units,
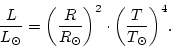 |
(12) |
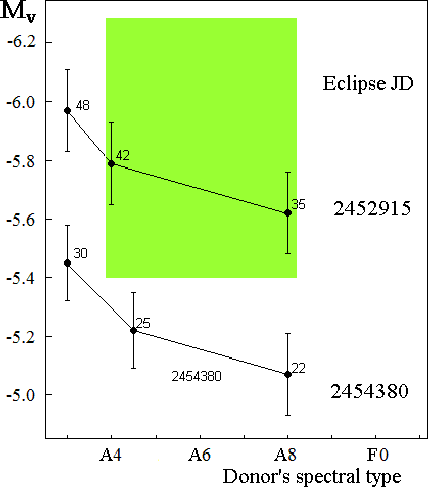 |
Fig. 10.
The spectral type - absolute
|
.
There is another question of interest. Can we detect, extract, or
measure the contribution of the donor star during an eclipse from
multicolor photometry knowing the possible range of its spectral
type, A4-A8? The spectral energy distributions of SS 433 during
eclipses (curves 2 in Fig. 9a,b) contain, besides the radiation
from the donor, also the radiation from the hot source (possibly
jet) eclipsed partially and the emission from the surrounding gas
envelope, which may include also an equatorially expanding
extended disk around the system described by Barnes et al. (2006,
Fig. 1). Barnes et al. show that the donor is visible during the
eclipse, near the precession phase
![]() , being not
shielded by the extended disk. Using the Subaru and BTA spectra, I
measured the emission contribution in the
, being not
shielded by the extended disk. Using the Subaru and BTA spectra, I
measured the emission contribution in the ![]() ,
, ![]() , and
, and ![]() filters in the eclipse of 2007 October 6; the results are given in
Table 4. The averages of these contributions to the
filters in the eclipse of 2007 October 6; the results are given in
Table 4. The averages of these contributions to the ![]() filters
were subtracted from the intensities of light during eclipses
(curves 2, Fig. 8 and 9), to get a pure continuum distribution in
eclipses (curves 3). Note that the same emission-line
contributions were subtracted also from the energy distribution of
the 2003 October 1 eclipse because those observations were not
accompanied by spectroscopy.
filters
were subtracted from the intensities of light during eclipses
(curves 2, Fig. 8 and 9), to get a pure continuum distribution in
eclipses (curves 3). Note that the same emission-line
contributions were subtracted also from the energy distribution of
the 2003 October 1 eclipse because those observations were not
accompanied by spectroscopy.
The unreddened ![]() colors of HD 12027 (A3III), HD 240296
(A6III), and HD 12161 (A8III) were taken from Table 2 in Jacoby,
Hunter, & Christian (1984) as examples of A-star colors. I
plotted the spectral energy distributions of these stars in Fig. 9
as blue curves, for comparison, so that they intersect in the
colors of HD 12027 (A3III), HD 240296
(A6III), and HD 12161 (A8III) were taken from Table 2 in Jacoby,
Hunter, & Christian (1984) as examples of A-star colors. I
plotted the spectral energy distributions of these stars in Fig. 9
as blue curves, for comparison, so that they intersect in the
![]() -band range; the
-band range; the ![]() -band intensity was used as a free
parameter. Then I removed some portions of hot-source energy
distributions (curves 4) from the eclipse-center energy
distributions corrected for emission (curves 3), to find, in the
residuals, an energy distribution resembling that of an A star
(see curves 5 in Fig. 9). This is easy to do because a real star
with a large Balmer jump is present in each of the two energy
distributions. Accurately adjusting the subtracted hot-source
energy distribution (curve 4) and the
-band intensity was used as a free
parameter. Then I removed some portions of hot-source energy
distributions (curves 4) from the eclipse-center energy
distributions corrected for emission (curves 3), to find, in the
residuals, an energy distribution resembling that of an A star
(see curves 5 in Fig. 9). This is easy to do because a real star
with a large Balmer jump is present in each of the two energy
distributions. Accurately adjusting the subtracted hot-source
energy distribution (curve 4) and the ![]() -band intensity of the
template, one can fit the residual distribution with any star,
from A3 to A6. In the case of best fitting,
-band intensity of the
template, one can fit the residual distribution with any star,
from A3 to A6. In the case of best fitting, ![]() -band intensity of
the sample corresponds to unreddened visible
-band intensity of
the sample corresponds to unreddened visible ![]() magnitude of the
donor. Certainly, the visible magnitude, absolute magnitude, and
donor's contribution to the combined light (which is calculated
for the
magnitude of the
donor. Certainly, the visible magnitude, absolute magnitude, and
donor's contribution to the combined light (which is calculated
for the ![]() band) depend on the energy distribution of the
template chosen for fitting and on the amount of hot-source
radiation. The results of residuals fitting are shown in Fig. 10
for each eclipse as points with error bars; the contribution of
the A-type donor to the
band) depend on the energy distribution of the
template chosen for fitting and on the amount of hot-source
radiation. The results of residuals fitting are shown in Fig. 10
for each eclipse as points with error bars; the contribution of
the A-type donor to the ![]() band, estimated from each fitting and
expressed in percents, is indicated by numbers near each point. It
appears from Fig. 10 that the absolute magnitudes derived from
photometry are systematically fainter than those derived from
spectroscopy. Additionally, the derived absolute magnitudes of the
donor change from eclipse to eclipse, so that their error bars do
not overlap. The nature of these systematical differences is not
yet clear. Using the two eclipses, we find the following
absolute-magnitude limits:
band, estimated from each fitting and
expressed in percents, is indicated by numbers near each point. It
appears from Fig. 10 that the absolute magnitudes derived from
photometry are systematically fainter than those derived from
spectroscopy. Additionally, the derived absolute magnitudes of the
donor change from eclipse to eclipse, so that their error bars do
not overlap. The nature of these systematical differences is not
yet clear. Using the two eclipses, we find the following
absolute-magnitude limits:
![]() , for the
donor spectra in the A4-A8 range.
, for the
donor spectra in the A4-A8 range.
6. THE MASS-LUMINOSITY RELATION
The Russell-Vogt theorem states that if we know a star's mass and
its chemical composition, then, using laws of physics, we can
determine all of its other properties, such as luminosity, radius,
temperature and density profiles, and find how these properties
change with time (Massey & Meyer, 2001). A. Eddington was the
first to demonstrate that radiative diffusion in stars required a
dependence of the stellar luminosity on mass, ![]() . Since
Eddington times, stellar luminosities are known from evolutionary
modeling. Modeling shows a good mass-luminosity relation for
main-sequence stars with hydrogen burning in their centers. But
low-mass stars, like those in globular clusters, can reach high
luminosities during late stages of their evolution, for example,
the stage of a red giant with a degenerate helium core or the
stage of an AGB star with a degenarate carbon core. Such stars
deviate far from the general relation though for a comparatively
short time. Other unaccounted effects in this theory, like
rotation or binarity, can lead to violations of the relationship.
. Since
Eddington times, stellar luminosities are known from evolutionary
modeling. Modeling shows a good mass-luminosity relation for
main-sequence stars with hydrogen burning in their centers. But
low-mass stars, like those in globular clusters, can reach high
luminosities during late stages of their evolution, for example,
the stage of a red giant with a degenerate helium core or the
stage of an AGB star with a degenarate carbon core. Such stars
deviate far from the general relation though for a comparatively
short time. Other unaccounted effects in this theory, like
rotation or binarity, can lead to violations of the relationship.
Star masses can be determined from observations if we apply
dynamic methods to visual, eclipsing, or spectroscopic binaries,
mostly detached systems. Certainly, the knowledge of accurate
distances and luminosities is needed for such systems. Using this
method for semidetached or contact binaries faces the problems
described in this paper for the case of SS 433. Besides, it is
possible to estimate a star's mass from high-resolution
spectroscopy and stellar-atmosphere modeling. Fitting the observed
line profiles to model ones gives the effective temperature
![]() and surface gravity
and surface gravity ![]() . If the star's distance and
luminosity are known, one can calculate its radius from the
Stephan-Boltzmann law (cf. eq. (12)), and then its mass from the
relation
. If the star's distance and
luminosity are known, one can calculate its radius from the
Stephan-Boltzmann law (cf. eq. (12)), and then its mass from the
relation ![]() (Massey & Meyer, 2001).
(Massey & Meyer, 2001).
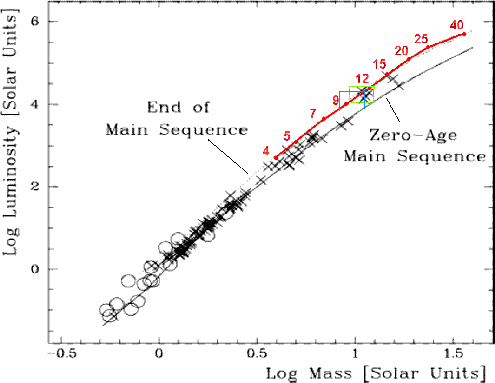 |
Fig. 11. A fragment of the mass-luminosity diagram by Massey & Meyer (2001, Fig. 1) constructed for components of binary stars. The theoretical mass-luminosity relation derived by the author for A stars using the models by Schaller et al. (1992) is also plotted (red points and lines). There is an agreement with observations of binary components. The localization of SS 433 A-type donor is marked with two error boxes, the green box being the localization revealed from spectroscopy and the blue box, from photometry. |
I analyzed the mass-luminosity relation for A-type stars using
the evolutionary models by Schaller et al. (1992), specifically
their evolutionary tracks for a nearly-solar chemical composition
(Y = 0.30, Z = 0.020, their Fig. 1). Massive and luminous stars
became A stars on their tracks to red giants. The evolution of
massive stars to the red side of the C-M diagram goes at a
constant luminosity, and hence the theoretical mass-luminosity
relation is determined correctly, with an insignificant
dispersion. The theoretical mass-luminosity relation for A stars
is presented in Table 5. In Fig. 11, this relation is plotted over
a fragment of the mass-luminosity diagram presented in Fig. 1 of
Massey & Meyer (2001), which was constructed for components of
binary stars. The relation for A stars is plotted as red points
and a red broken line; the red numbers are initial masses of the
models. Along the abscissa, current masses of A-star models are
plotted: stellar models were computed with the mass loss taken
into account. In the luminosity ranges of interest, the mass loss
of single stars that become A stars varies from
![]() for the initial mass of
for the initial mass of ![]() to
to
![]() for
for ![]() . Figure 11 shows that the A-star relation coincides with
the location of stars at the end of the main sequence, whereas the
stars on the zero-age main sequence have larger masses for their
luminosities. Our comparison of the theory with observations of
star-system components reveals a good agreement.
. Figure 11 shows that the A-star relation coincides with
the location of stars at the end of the main sequence, whereas the
stars on the zero-age main sequence have larger masses for their
luminosities. Our comparison of the theory with observations of
star-system components reveals a good agreement.
SS 433 is not a single star, and the donor is losing mass at a
higher rate than a single star, but the current bolometric
luminosity of the donor should reflect its current mass.
Principally, the bolometric absolute magnitude does not depend on
the star's spectrum (or on ![]() on its surface), it depends
on the energy release in the stellar interior. Eventually,
however, the energy release depends on stellar mass.
on its surface), it depends
on the energy release in the stellar interior. Eventually,
however, the energy release depends on stellar mass.
When using the theoretical relationship for A stars to estimate the donor mass in SS 433, the question arises if this star has an internal structure similar to normal single stars with the same spectral types and luminosities. Actually, the volume of a star in a binary system is limited by the critical equipotential surface. A component of a binary evolving to the stage of degenerate helium core would not be able to become a red giant because its expanding envelope will overflow to the secondary component or flow away from the system. Such phenomena are observed in SS 433. A star with a forming helium core may have excess luminosity compared to a single star of the same mass. Using the relation for single stars, we will overestimate the mass of such a component. A common-envelope phase in a binary with an expanding component is also possible, and this can be just the case for the system of SS 433.
For masses exceeding ![]() , loops of evolutionary tracks
occurring in the He-burning phase get into the region of A stars
at somewhat higher luminosities than the luminosity on the way to
red giants. The He-burning phase on such a loop seems improbable
for the SS 433 donor. However, using the mass-luminosity relation
for A stars in such a case, we will also overestimate the mass of
the SS 433 donor. This means that if we use the mass-luminosity
relation for A stars derived using tracks to red giants but the
real A star is at a later evolutionary stage and its envelope is
limited by the binary's equipotential surface, then its mass will
actually be lower, and lower will be the mass of the compact
object.
, loops of evolutionary tracks
occurring in the He-burning phase get into the region of A stars
at somewhat higher luminosities than the luminosity on the way to
red giants. The He-burning phase on such a loop seems improbable
for the SS 433 donor. However, using the mass-luminosity relation
for A stars in such a case, we will also overestimate the mass of
the SS 433 donor. This means that if we use the mass-luminosity
relation for A stars derived using tracks to red giants but the
real A star is at a later evolutionary stage and its envelope is
limited by the binary's equipotential surface, then its mass will
actually be lower, and lower will be the mass of the compact
object.
The donor's mass determined from this relation, in agreement with
its light contribution estimated spectroscopically, falls in the
range from 9.4 to ![]() , while the mass estimated
photometrically is between 8.3 and
, while the mass estimated
photometrically is between 8.3 and ![]() . The error boxes
of the parameters derived for the donor are shown in Fig. 11 as
rectangles. The green rectangle corresponds to the
spectroscopically determined contribution in eclipse, and the blue
rectangle corresponds to that determined photometrically. The
location of the error boxes is in agreement with models for
evolved stars that leaved the main sequence.
. The error boxes
of the parameters derived for the donor are shown in Fig. 11 as
rectangles. The green rectangle corresponds to the
spectroscopically determined contribution in eclipse, and the blue
rectangle corresponds to that determined photometrically. The
location of the error boxes is in agreement with models for
evolved stars that leaved the main sequence.
The mass ![]() of the compact object can be calculated using the
formula
of the compact object can be calculated using the
formula ![]() , where
, where ![]() is the mass of the A-type donor
and
is the mass of the A-type donor
and
![]() is the mass ratio known from observations
of the jet eclipse in X-rays.
is the mass ratio known from observations
of the jet eclipse in X-rays.
 |
Fig. 12.
Mass estimates for the compact
object based on the estimates of A-type donor luminosities. As in
Fig. 10, the green rectangle is the region of spectroscopic
solutions. Points with error bars connected with broken lines are
photometric solutions for the mass revealed from photometry of the
two eclipses. A number printed near each point is the |
Now, having in mind all these considerations and using the small
bolometric corrections, in the range between
![]() and
+0
and
+0![]() 09, respectively for A4I-III and A8I-III, we translate all
the regions and points shown in Fig. 10 (the spectral type-
09, respectively for A4I-III and A8I-III, we translate all
the regions and points shown in Fig. 10 (the spectral type-![]() diagram) to the donor's spectral type-compact-object mass diagram
for SS 433 (Fig. 12).
diagram) to the donor's spectral type-compact-object mass diagram
for SS 433 (Fig. 12).
Figure 12 demonstrates that all mass estimates are concentrated
near the level of the Chandrasekhar limit established for zero-age
neutron stars, ![]() (blue line), but essentially below
the lower mass limit for stellar-mass black holes,
(blue line), but essentially below
the lower mass limit for stellar-mass black holes, ![]() (red line). Note that wrong identification of the donor's
evolutionary stage would lead to smaller mass estimates for the
compact component, and its mass will still be below the
Chandrasekhar limit.
(red line). Note that wrong identification of the donor's
evolutionary stage would lead to smaller mass estimates for the
compact component, and its mass will still be below the
Chandrasekhar limit.
Our final mass estimates for the compact object in SS 433 are
![]() for the donor's light contribution in the
eclipse near
for the donor's light contribution in the
eclipse near ![]() derived spectroscopically and
derived spectroscopically and
![]() for that derived photometrically and based on the donor's
spectral type estimated from spectroscopy as A4
for that derived photometrically and based on the donor's
spectral type estimated from spectroscopy as A4 ![]() A8 I
A8 I![]() III.
III.
To check if the masses of the components of SS 433 agree with laws
of physics, let us calculate the amplitudes of radial-velocity
curves ![]() for the A-type donor and
for the A-type donor and ![]() for the compact object
from the formulae of Keplerian dynamics:
for the compact object
from the formulae of Keplerian dynamics:
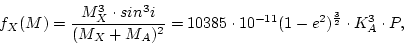 |
(13) |
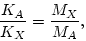 |
(14) |
Let us now conversely calculate the magnitude of the donor star
using the mass of ![]() for the compact object from Kubota
et al. (2010) and
for the compact object from Kubota
et al. (2010) and ![]() , the mass of a hypothetical black
hole at the lower limit of black-hole masses. With the mass ratio
, the mass of a hypothetical black
hole at the lower limit of black-hole masses. With the mass ratio
![]() = 0.15 and the mass-luminosity relation deduced from Shaller
et al. (1992), I estimated masses, absolute
= 0.15 and the mass-luminosity relation deduced from Shaller
et al. (1992), I estimated masses, absolute ![]() magnitudes, and
magnitudes, and
![]() -band visible reddened magnitudes of the A-type donor stars as
respectively 28.7 and
-band visible reddened magnitudes of the A-type donor stars as
respectively 28.7 and ![]() ,
,
![]() and
and
![]() ,
12
,
12![]() 67 and 13
67 and 13![]() 55. Note that SS 433 has a maximum normal
brightness of 13
55. Note that SS 433 has a maximum normal
brightness of 13![]() 9-14
9-14![]() 0 in the
0 in the ![]() band, and its brightness
reaches 13
band, and its brightness
reaches 13![]() 55 only in outbursts. This is the combined
brightness of all components and light sources in the binary.
Thus, black-hole masses are in a strong conflict with the results
of photometry.
55 only in outbursts. This is the combined
brightness of all components and light sources in the binary.
Thus, black-hole masses are in a strong conflict with the results
of photometry.
7. DISCUSSION
The general parameters used in this paper, such as distance,
extinction, A-star contribution during eclipses near the ![]() precession phase are no surprise. They were repeatedly examined in
different studies. The contribution of the A-type donor measured
in this paper,
precession phase are no surprise. They were repeatedly examined in
different studies. The contribution of the A-type donor measured
in this paper, ![]() percents in the
percents in the ![]() band,
photometrically corresponds to a magnitude between 15.7 and 16.4.
This range is in conflict with the magnitude of 17.35 in the
band,
photometrically corresponds to a magnitude between 15.7 and 16.4.
This range is in conflict with the magnitude of 17.35 in the ![]() band measured in an eclipse, at the
band measured in an eclipse, at the ![]() phase, by Henson et al.
(1982). However, this contradiction can be easily understood if we
remember the circumbinary equatorial expanding and precessing
disk, well illustrated by Barnes et al. (2006), which covers the
system partly in the precession phases near
phase, by Henson et al.
(1982). However, this contradiction can be easily understood if we
remember the circumbinary equatorial expanding and precessing
disk, well illustrated by Barnes et al. (2006), which covers the
system partly in the precession phases near ![]() and
and ![]() . The
known dependence of eclipse depth on the precession phase with the
amplitude of 0
. The
known dependence of eclipse depth on the precession phase with the
amplitude of 0![]() 40 can be explained with this disk, too. The
eclipse observed by Henson et al. was monitored also by Gladyshev
et al. (1987), and it is known that,
40 can be explained with this disk, too. The
eclipse observed by Henson et al. was monitored also by Gladyshev
et al. (1987), and it is known that,
![]() before and
before and
![]() after the observation by Henson et al., the brightness
of SS 433 was extraordinary high for those orbital and precession
phases, so the object was in a high state. Probably, a time was
caught when the circumbinary disk was extraordinary thick and
covered the donor totally. This event could coincide with a
short-duration weakening of the jets. Such an event was unique but
observationally well established.
after the observation by Henson et al., the brightness
of SS 433 was extraordinary high for those orbital and precession
phases, so the object was in a high state. Probably, a time was
caught when the circumbinary disk was extraordinary thick and
covered the donor totally. This event could coincide with a
short-duration weakening of the jets. Such an event was unique but
observationally well established.
The nature of the circumbinary disk remains unclear yet. It is observed in radio bands as a wind of rapidly varying shape at the distances of about 200-250 AU and is resolved (Paragi et al., 1999). This structure is perpendicular to radio jets. The radio structure is discussed in detail in the review by Fabrika (2004); see additional references there. The disk may be formed by gas flowing out from the external Lagrangian point L2. It is unclear why this gas, which covers the central jet bases, does not form an absorption-line spectrum in the optical bands.
With the A-star contribution of ![]() percents in the
percents in the ![]() band in minimum light, its contribution is only 10-20 percents in
maximum light. It is clear from an inspection of Fig. 2, where the
light curve near
band in minimum light, its contribution is only 10-20 percents in
maximum light. It is clear from an inspection of Fig. 2, where the
light curve near ![]() has a
has a ![]() -Lyrae-like shape with a
large-amplitude "ellipsoidal effect" and a secondary eclipse
0
-Lyrae-like shape with a
large-amplitude "ellipsoidal effect" and a secondary eclipse
0![]() 4 deep, that neither the ellipsoidal effect no the secondary
eclipse can be related to the donor because of its small light
contribution. The main bright source in the
4 deep, that neither the ellipsoidal effect no the secondary
eclipse can be related to the donor because of its small light
contribution. The main bright source in the ![]() band is the very
hot one, covered partially in the primary eclipse. Then its
contribution in maximum light is up to 77-87 percents, taking
into account the 3-percent contribution of the
emission-line-radiating envelope. If this is a hot disk or another
rapidly rotating body, it also cannot form either the ellipsoidal
effect or the deep secondary eclipse. Otherwise, the source may be
a star filling the Roche lobe of the compact component and having
an elongated shape due to the gravitational influence of the
donor. Thus, the hypothesis of a "supercritical accretion disk"
in SS 433 is a myth, and it is not confirmed with the photometry.
It is not correct to fit the optical light curves by a model of a
thick precessing disk plus a gravitationally distorted OB star, as
that was done by Antokhina & Cherepashchuk (1985, 1987).
Moreover, we do not see any details in the photometry that could
be treated as external contacts of a bright star filling the Roche
lobe of the compact component, though we know that the eclipse of
the Roche lobe is total due to the small ratio,
band is the very
hot one, covered partially in the primary eclipse. Then its
contribution in maximum light is up to 77-87 percents, taking
into account the 3-percent contribution of the
emission-line-radiating envelope. If this is a hot disk or another
rapidly rotating body, it also cannot form either the ellipsoidal
effect or the deep secondary eclipse. Otherwise, the source may be
a star filling the Roche lobe of the compact component and having
an elongated shape due to the gravitational influence of the
donor. Thus, the hypothesis of a "supercritical accretion disk"
in SS 433 is a myth, and it is not confirmed with the photometry.
It is not correct to fit the optical light curves by a model of a
thick precessing disk plus a gravitationally distorted OB star, as
that was done by Antokhina & Cherepashchuk (1985, 1987).
Moreover, we do not see any details in the photometry that could
be treated as external contacts of a bright star filling the Roche
lobe of the compact component, though we know that the eclipse of
the Roche lobe is total due to the small ratio, ![]() . No
contribution of such a star, which may have an energy distribution
different from that of the very hot source, is also detectable in
multicolor photometry. It is small compared to the A-type donor
contribution.
. No
contribution of such a star, which may have an energy distribution
different from that of the very hot source, is also detectable in
multicolor photometry. It is small compared to the A-type donor
contribution.
In such a case, we may expect that the light distribution of the
hot source in SS 433 is formed only by jet bases and holes or
nozzles the jets come from. The "ellipsoidal effect", the
precession light variations, and the "secondary eclipse" of the
very hot light source are present only due to effects of
visibility of the nozzle depths and jets' bases. Near precession
phases ![]() and
and ![]() , the dispersion of light curves increases
strongly (Fig. 2); the causes of this phenomenon may be both the
system being covered by the nonuniform structure of the
hypothetical circumbinary disk and variations of visibility
conditions of nozzle depths due to uneven and rough structure of
nozzles' edges. The hypothesis that the light curves of SS 433
could be explained by the motion of two bright hot spots at the
points of emergence of the jets (or jet nozzles), while the
contribution of the disk or its envelope to the total brightness
was small, was first put toward by Lipunov & Shakura (1982).
, the dispersion of light curves increases
strongly (Fig. 2); the causes of this phenomenon may be both the
system being covered by the nonuniform structure of the
hypothetical circumbinary disk and variations of visibility
conditions of nozzle depths due to uneven and rough structure of
nozzles' edges. The hypothesis that the light curves of SS 433
could be explained by the motion of two bright hot spots at the
points of emergence of the jets (or jet nozzles), while the
contribution of the disk or its envelope to the total brightness
was small, was first put toward by Lipunov & Shakura (1982).
Another important factor in forming the optical light curve can be
variable brightness of jets. Hydrogen burning on the surface of a
neutron star is very unstable, because a critical mass should be
accumulated repeatedly for the ignition. Repeated ignitions may be
the cause of forming the bullets. Appearance of bullets in the
moving Balmer lines means that the matter of jets is thrown out in
portions. The connection of the bullet formation to the optical
variations has not yet been studied. However, this effect can
cause deviations of individual minima from the linear ephemeris
found in my study. Additionally, the jets are driven by tidal
waves responsible for nodding motion. Fourier analysis of our
photometry also shows a significant wave with an amplitude of
about 0![]() 2 and the same period as that of nodding motion of the
moving H
2 and the same period as that of nodding motion of the
moving H![]() components in the spectra, 6
components in the spectra, 6![]() 2887 (Goranskij
et al., 1998a).
2887 (Goranskij
et al., 1998a).
I assume that, in the case of a contact system in SS 433 having a neutron star in the center of a component filling the Roche lobe, the products of hydrogen burning on the surface of the neutron star are channelling out of the star through the nozzles throwing most of the thermonuclear energy into space. Therefore, the surface of such a star with the neutron star inside can be heated insufficiently to contribute to the common light of the system. I think that cases of supercritical accretion on a black hole and of hydrogen burning on the surface of a neutron star differ in the chemical composition of matter erupted in jets. Indeed, no thermonuclear burning is possible if the matter falls into a black hole. It should be also reminded that Lipunov & Shakura (1982) demonstrated the liberation of energy through the accretion process on a neutron star to be the only process capable of explaining the energy release of SS 433.
The conclusions of this study are strongly dependent on the mass
ratio ![]() established from X-ray observations of the Ginga
satellite. I assume that it is a very reliable result because the
eclipse contacts were observed not only in continuum radiation but
also in the moving emission blend of Fe XXV/Fe XXVI radiated by
the jets. This circumstance permits to correctly localize the
eclipsed source. The contacts and width of the X-ray eclipse are
confirmed with the X-ray observations in continuum. Another
confirmation of the mass ratio being so small is the radial
velocity of the stationary H
established from X-ray observations of the Ginga
satellite. I assume that it is a very reliable result because the
eclipse contacts were observed not only in continuum radiation but
also in the moving emission blend of Fe XXV/Fe XXVI radiated by
the jets. This circumstance permits to correctly localize the
eclipsed source. The contacts and width of the X-ray eclipse are
confirmed with the X-ray observations in continuum. Another
confirmation of the mass ratio being so small is the radial
velocity of the stationary H![]() line, which is displaced by
90 degrees in orbital phase. The maximum recessive velocity in
H
line, which is displaced by
90 degrees in orbital phase. The maximum recessive velocity in
H![]() is observed in the inferior conjunction of the donor,
i.e. in eclipse. The equivalent width of the H
is observed in the inferior conjunction of the donor,
i.e. in eclipse. The equivalent width of the H![]() line
increases in eclipse due to deep eclipse in continuum, but the
intensity of the line does not show any eclipse. This means that
the line is radiated in an extensive and expanding envelope.
line
increases in eclipse due to deep eclipse in continuum, but the
intensity of the line does not show any eclipse. This means that
the line is radiated in an extensive and expanding envelope.
Goranskij et al. (1997) found a natural explanation for this
phenomenon. In this system, a part of the envelope is located in a
shadow of the companion. The companion covers the radiation of the
hot source for the shadow cone, gas in the shadow rapidly
recombines, and it cannot be excited by the hot source for the
eclipse duration. The opposite side of the A-type donor, which has
strong and wide Balmer and Lyman absorption lines, is not able to
effectively excite the hydrogen in the shadow. The angle of the
shadow cone, the volume of neutral gas in the envelope, the lost
emission intensity, due to the shadow, in the line profiles, and
the amplitude of the velocity curve based on mean-profile
intensity variations depend strongly on the distance of the hot
exciting source from the donor's surface, and therefore on the
mass ratio ![]() . My simple profile modeling with the Monte Carlo
method shows that the observed amplitude of 160 km s
. My simple profile modeling with the Monte Carlo
method shows that the observed amplitude of 160 km s![]() is
best fitted with the mass ratio
is
best fitted with the mass ratio ![]() . Thus, the displacement
of the H
. Thus, the displacement
of the H![]() radial velocity curve is an additional argument
in favor of a low mass ratio and low mass of the compact
component.
radial velocity curve is an additional argument
in favor of a low mass ratio and low mass of the compact
component.
Kubota et al. (2010) try to disprove this argument restricting it
only to "wind evacuation", i.e. to covering the wind cone by the
donor, with the wind being formed by the accretion disk. They
thought this covering led to an anisotropic wind. Their arguments
against the shadow hypothesis are weak. The first one is that the
radial velocity amplitudes of H and HeI have to exceed those of
the accretion disk (traced by the HeII line) since the disk powers
the wind. The presence of such a disk has not yet been proven, the
most questionable is the hypothesis of forming the HeII line by
the disk. The behavior of the HeII line in eclipse described above
does not confirm its relation to the disk. No partial or total
eclipses in H and HeI emission have been observed yet. Different
amplitudes of H and HeI lines can be explained with different
excitation conditions: the A-type donor has much weaker lines of
HeI than those of H, and HeI atoms can be excited with a larger
probability. The second argument is related to the accretion gas
stream. If a gas stream drawn in the sketch in Fig. 13 in Kubota
et al. (2010) really exists, it should be located near the L1
Lagrangian point between the stars and thus should be totally
eclipsed in the phase range wider than that of the jet-base
eclipse because the L1 Lagrangian point is closer to the donor
than the jet bases. Even if located in the drawn place, the gas
stream should be eclipsed totally but in the different range of
orbital phases. Nothing of this behavior was observed.
Additionally, H![]() has a wide profile with
has a wide profile with
![]() Å, corrected for instrumental resolution in the
spectra, so one should find a hypothetical stream component in the
profile formed by the expanding wind with the velocity of about
750 km s
Å, corrected for instrumental resolution in the
spectra, so one should find a hypothetical stream component in the
profile formed by the expanding wind with the velocity of about
750 km s![]() and exhibiting wide eclipses. Recently, Bowler
(2009) detected a transient component in the profile of the
H
and exhibiting wide eclipses. Recently, Bowler
(2009) detected a transient component in the profile of the
H![]() emission, subject to Doppler effect with the orbital
period, at a speed of approximately 175 km s
emission, subject to Doppler effect with the orbital
period, at a speed of approximately 175 km s![]() , but this
component is not eclipsed at any orbital phase (the mass he
estimated for the compact object is less than
, but this
component is not eclipsed at any orbital phase (the mass he
estimated for the compact object is less than ![]() ).
Bowler attributes this component to the accretion disk around the
compact companion.
).
Bowler attributes this component to the accretion disk around the
compact companion.
Thus, there exists additional evidence for a very small mass ratio for the components of SS 433 besides the Ginga X-ray observations in eclipses. Since Ginga times, new perfect X-ray observatories and devices have been launched into space and work successfully. One of such observatories is Chandra. Its HETGS spectrograph has a higher resolution and sensitivity than that of Ginga. In variance with Ginga, this device resolves the FeXXV/FeXXVI blend at 6 keV (Marshall et al., 2002). The Chandra team did not repeat the Ginga experiment aimed at detecting jet contact times during eclipses, but public releases at the Chandra Internet site are full with declarations that SS 433 is a black-hole binary. Why not check Ginga data with the modern Chandra observations?
Another problem which may have an improved solution is the mass
![]() luminosity relation for A-type stars with high accretion rate
caused by the evolution with the Roche-lobe-limited envelopes. In
this study, it was naturally supposed that A-type stars that had
lost their mass from the envelope evolved as single stars but with
a smaller, residual mass. But it is of interest to solve this
problem by modeling. It seems that this problem is not so
difficult.
luminosity relation for A-type stars with high accretion rate
caused by the evolution with the Roche-lobe-limited envelopes. In
this study, it was naturally supposed that A-type stars that had
lost their mass from the envelope evolved as single stars but with
a smaller, residual mass. But it is of interest to solve this
problem by modeling. It seems that this problem is not so
difficult.
As a critical reader of my paper may note, I used, in Section 2,
the filter transmission curves collected by Moro & Munari (2000)
for the original Johnson and Cousins photometric systems, but not
those for the instrumental ![]() bands used in our
measurements with the SAO 1-m telescope. Accurate studies of such
curves for the instrumental systems need special devices, like a a
monochromator, and techniques of high-precision photometry
described by Mironov (2008). Additionally, my experience shows
that high-precision CCD photometry also needs special measures to
prevent flashes originating from skew light reflection on the
surfaces parallel to the optical axis of the telescope, such as
the Cassegrain blend or cylindrical photometer details, even
blackened. For precise CCD photometry, it would be preferable to
have a special photometric telescope with a CCD detector in the
prime focus, without any blend. However, we have to use
multi-purpose telescopes, not prepared specially for precise
photometry. This certainly affects adversely the accuracy of
flat-field calibration and standard measurements. The absence of
spectroscopy in the red spectral range is another perceptible
drawback of this study. We used the available data as is.
Performing absolutely correct photometry of SS 433, supported with
spectroscopy with big telescopes, seems a difficult problem.
bands used in our
measurements with the SAO 1-m telescope. Accurate studies of such
curves for the instrumental systems need special devices, like a a
monochromator, and techniques of high-precision photometry
described by Mironov (2008). Additionally, my experience shows
that high-precision CCD photometry also needs special measures to
prevent flashes originating from skew light reflection on the
surfaces parallel to the optical axis of the telescope, such as
the Cassegrain blend or cylindrical photometer details, even
blackened. For precise CCD photometry, it would be preferable to
have a special photometric telescope with a CCD detector in the
prime focus, without any blend. However, we have to use
multi-purpose telescopes, not prepared specially for precise
photometry. This certainly affects adversely the accuracy of
flat-field calibration and standard measurements. The absence of
spectroscopy in the red spectral range is another perceptible
drawback of this study. We used the available data as is.
Performing absolutely correct photometry of SS 433, supported with
spectroscopy with big telescopes, seems a difficult problem.
The best solution of this problem seems to be spectrophotometry with a wide and long slit to prevent light losses at the slit, but at the cost of spectral resolution. Such observations require spectrophotometric standards in the close vicinity of SS 433. However, establishing such standards is not a difficult problem.
8. CONCLUSIONS
In this paper, it is reliably established on the base of current
knowledge of distance, extinction, mass ratio, and contribution of
A-type star for SS 433, along with modern data on stellar
photomery, its physical calibration, stellar bolometric
corrections, temperature calibrations, mass-luminosity ratio that
the compact object in the system of SS 433 is a neutron star with
a mass close to the Chandrasekhar limit, ![]() . This
conclusion follows from the discovery of an A4-A8I-III star in
the spectrum. With all possible estimates of the A-star's
contribution to the combined light of the system during the
eclipse, the mass of the neutron star is in the range between 1.25
and
. This
conclusion follows from the discovery of an A4-A8I-III star in
the spectrum. With all possible estimates of the A-star's
contribution to the combined light of the system during the
eclipse, the mass of the neutron star is in the range between 1.25
and ![]() . The mass of the neutron star is
. The mass of the neutron star is
![]() solely from multicolor photometry.
solely from multicolor photometry.
To adopt the assumption of a black hole, the basic parameters of SS 433 and main astrophysical data should be radically revised.
Acknowledgments:
The author thanks A.V. Mironov (Sternberg Astronomical Institute, Moscow University) for his help in some questions of stellar photometry and its calibration.
References:
Antokhina, E. A., Cherepashchuk, A. M., 1985, Soviet Astron. Letters, 11, 4
Antokhina, E. A., Cherepashchuk, A. M., 1987, Soviet Astron., 31, 295
Aslanov, A. A., Cherepashchuk, A. M., Goranskij, V. P., et al., 1993, Astron. & Astrophys., 270, 200
Barnes, A. D., Casares, J., Charles, P. A., et al., 2006, Monthly Not. Roy. Astron. Soc., 365, 296
Blundell, K. M., Bowler, M. G., 2004, Astrophys. J., 616, L159
Bohlin, R. C., Gilliland, R. L., 2004, Astron. J., 127, 3508
Borisov, N. V., Fabrika, S. N., 1987, Soviet Astron. Letters, 13, 200
Bowler, M. G., 2009, arXiv:0912.2428
Brinkmann, W., Kawai, N., Matsuoka, M., 1989, Astron. & Astrophys., 218, L13
Brinkmann, W., Kotani, T., Kawai, N., 2005, Astron. & Astrophys., 431, 575
Cherepashchuk, A. M., 1981, Monthly Not. Roy. Astron. Soc., 194, 761
Cherepashchuk, A. M., Aslanov, A. A., Kornilov, V. G., 1982, Soviet Astron., 26, 697
Cherepashchuk, A. M., Sunyaev, R. A., Fabrika, S. N., et al., 2005, Astron. & Astrophys., 437, 561
Crampton, D., Hutchings, J. B., 1981, Astrophys. J., 251, 604
Davydov, V. V., Esipov, V. F., Cherepashchuk, A. M., 2008, Astron. Reports, 52, 487
Fabrika, S. N., 2004, Astrophys. & Space Phys. Rev., 12, 1
Fabrika, S. N., Bychkova, L. V., 1990, Astron. & Astrophys., 240, L5
Fejes, I., 1986, Astron. & Astrophys., 168, 69
Gies, D. R., Huang, W., McSwain, M. V., 2002a, Astrophys. J., 578, L67
Gies, D. R., McSwain, M. V., Riddle, R. L., et al., 2002b, Astrophys. J., 566, 1069
Gladyshev, S. A., Goranskij, V. P., Kurochkin, N. E., Cherepashchuk, A. M., 1980, Astron. Tsirkulyar, No. 1145
Gladyshev, S. A., 1981, Sov. Astron. Letters, 7, 330
Gladyshev, S. A., Goranskij, V. P. Cherepashchuk, A. M., 1987, Soviet Astron., 31, 541
Goranskii, V. P., Fabrika, S. N., Rakhimov, V. Yu., et al., 1997, Astron. Reports, 41, 656
Goranskii, V. P., Esipov, V. F., Cherepashchuk, A. M., 1998a, Astron. Reports, 42, 209
Goranskii, V. P., Esipov, V. F., Cherepashchuk, A. M. 1998b, Astron. Reports, 42, 336
Goranskij, V. P., 1998c, in: Proc. of the 20-th Conference on Variable Star Research, ed. J. Dushek, M. Zejda, Brno, Czech Republic, p.103
Grandi, S. A., Stone, R. P. S., 1982, Publ. Astron. Soc. Pacific, 94, 80
Henson, G., Kemp, J., Krauss, D., 1982, IAU Circ., No. 3750
Hillwig, T. C., Gies, D. R., Huang, W., McSwain, M. V., et al., 2004, Astrophys. J., 615, 422
Hillwig, T. C., Gies, D. R., 2008, Astrophys. J., 676, L37
Hjellming, R. M., Johnston, K. J., 1982, In: Extragalactic radio sources, Proceedings of the IAU Symposium No. 97, Dordrecht, D. Reidel Publishing Co. p. 197
Howarth, J. D., 1983, Monthly Not. Roy. Astron. Soc., 203, 301
Jacoby, G. H., Hunter, D. A., Christian, C. A., 1984, Astrophys. J. Suppl., 56, 257
Kawai, N., Matsuoka, M., Pan, H.-C., Stewart, G. C., 1989, Publ. Astron. Soc. Japan, 41, 461
Kemp, J. C., Henson, G. D., Kraus, D. J., et al., 1986, Astrophys. J., 305, 805
King, I., 1952, Astron. J., 57, 253
Koornneef, J., Code, A. D., 1981, Astrophys. J., 247, 860
Kotani, T., Kawai, N., Aoki, T., et al., 1994, Publ. Astron. Soc. Japan, 46, L147
Kubota, K., Ueda, Y., Fabrika, S., et al., 2010, Astrophys. J., 709, 1374
Lipunov, V. M., Shakura, N. I., 1982, Soviet Astron., 26, 386
Margon, B., Ford, H. C., Grandy, S. A., Stone, R. P. S., 1979, Astrophys. J., 233, L63
Margon, B., 1984, Annual Review Astron. Astrophys., 22, 507
Marshall, H. L., Canizares, C. R., Schulz, N. S., 2002, Astrophys. J., 564, 941
Massey, P., Meyer, M. R., 2001. Stellar Masses. In Encyclopedia of Astron. and Astrophysics, Nature Publishing Group
& Institute of Physics Publishing. Dirac House, Bristol, UK
(http://www.astro.caltech.edu/![]() george/ay20/eaa-stellarmasses.pdf)
george/ay20/eaa-stellarmasses.pdf)
Matthews, T. A., Sandage, A. R., 1963, Astrophys. J., 138, 30
Mironov, A. V., 2008, The Basics of Stellar Photometry, FizMatLit, Moscow, p. 207 (in Russian)
Moro, D., Munari, U., 2000, Astron. & Astrophys. Suppl. Series, 147, 361
Murdin, P., Clark, D. H., Martin, P. G., 1980, Monthly Not. Roy. Astron. Soc., 193, 135
Nandy, K., Morgan, D. H., Willis, A. J., et al., 1981, Monthly Not. Roy. Astron. Soc., 196, 955
Newsom, G. H., Collins II, G. W., 1981, Astron. J., 86, 1250
Newsom, G. H., Collins II, G. W., 1986, Astron. J., 91, 118
Paragi, Z., Vermeulen, R. C., Fejes, I., et al., 1999, Astron. & Astrophys., 348, 910
Prevot, M. L., Lequeux, J., Maurice E., et al., 1984, Astron. & Astrophys., 132, 389
Romney, J. D., Schilizzi, R. T., Fejes, I., Spencer, R.E., 1987, Astrophys. J., 321, 822
Savage, B. D., Mathys, J. S., 1979, Annual Review Astron. Astrophys., 17, 73
Schaller, G., Schaerer, D., Meynet, G., Maeder, A., 1992, Astron. & Astrophys. Suppl. Series, 96, 269
Schild, R.E., 1977, Astrophys. J., 82, 337
Seaton, M. J., 1979, Monthly Not. Roy. Astron. Soc., 187, 73P
Spencer, R. E., 1984, Monthly Not. Roy. Astron. Soc., 209, 869
Stephenson, C. B., Sanduleak, N., 1977, Astrophys. J. Suppl., 33, 459
Straizys, V., 1977, Multicolor Stellar Photometry, Mokslas, Vilnius (in Russian)
Straizys, V., Kuriliene, G., 1975, Bull. Vilnius Obs., No. 42, 16
Thorne, K. S., Zytkow, A. N., 1975, Astrophys. J., 199, L19
Thorne, K. S., Zytkow, A. N., 1977, Astrophys. J., 212, 832
Vermeulen, R. C., Murdin, P. G., van den Heuvel, E. P. J., et al., 1993a, Astron. & Astrophys., 270, 204
Vermeulen, R. C., Schilizzi, R. T., Spencer, R. E., et al., 1993b, Astron. & Astrophys., 270, 177
Wagner, R. M., Newsom, G. H., Foltz, C. B., Byard, P. L., 1981, Astron. J., 86, 1671
Wagner, R. M., 1986, Astrophys. J., 308, 152
Yuan, W., Kawai, N., Brinkmann, W., & Matsuoka, M., 1995, Astron. & Astrophys., 297, 451
| JD hel. | σ | ψ | Source | JD hel. | σ | ψ | Source | |
| 24... | days | 24... | days | |||||
| 44019.10 | 0.05 | 0.156 | G | 47394.310 | 0.03 | 0.955 | G | |
| 44332.73 | 0.05 | 0.088 | G | 47420.32 | 0.04 | 0.114 | G | |
| 44463.85 | 0.04 | 0.896 | G | 48035.06 | 0.05 | 0.903 | G | |
| 44476.93 | 0.03 | 0.975 | G | 48061.44 | 0.04 | 0.066 | G | |
| 44489.97 | 0.05 | 0.058 | G | 49840.52 | 0.04 | 0.030 | G | |
| 44790.89 | 0.06 | 0.910 | G | 49984.49 | 0.05 | 0.914 | F | |
| 44816.87 | 0.05 | 0.073 | G | 50965.88 | 0.05 | G | ||
| 45275.10 | 0.05 | 0.895 | G | 50978.61 | 0.10 | G | ||
| 45928.95 | 0.04 | 0.925 | G | 51763.84 | 0.05 | G | ||
| 45942.15 | 0.02 | 0.006 | G | 51776.82 | 0.05 | G | ||
| 45955.18 | 0.10 | 0.085 | G | 52758.00 | 0.05 | 0.009 | Ir | |
| 45968.46 | 0.10 | 0.167 | G | 52770.863 | 0.05 | 0.088 | Ch | |
| 46282.30 | 0.03 | 0.102 | G | 52914.77 | 0.08 | 0.975 | FG | |
| 46583.05 | 0.10 | 0.955 | G | 53582.14 | 0.02 | 0.088 | G | |
| 46596.10 | 0.04 | 0.037 | G | 53595.23 | 0.04 | 0.168 | G | |
| 46936.3047 | 0.013 | 0.133 | GI | 54079.06 | 0.10 | 0.150 | G: | |
| 46936.34 | 0.04 | 0.133 | G | 54380.33 | 0.02 | 0.006 | K | |
| 47093.250 | 0.03 | 0.099 | G | |||||
| G: from the author's data collection; GI: from Ginga X-ray observations; F: S.N. Fabrika; | ||||||||
| Ir: T.I. Irsmambetova; Ch: Cherepashchuk et al. (2005); FG: S.N. Fabrika & V.P. Goranskij; K: Kubota et al. (2010). | ||||||||
| Initial | Current |
|
||
| mass | mass | |||
| 4 | 4.0 | 0.602 | -2.10 | 2.740 |
| 5 | 5.0 | 0.699 | -3.00 | 3.100 |
| 7 | 7.0 | 0.845 | -4.35 | 3.640 |
| 9 | 8.99 | 0.956 | -5.24 | 3.996 |
| 12 | 11.90 | 1.076 | -6.22 | 4.338 |
| 15 | 14.70 | 1.167 | -7.02 | 4.708 |
| 20 | 19.06 | 1.280 | -8.18 | 5.172 |
| 25 | 23.62 | 1.373 | -8.70 | 5.380 |
| 40 | 36.06 | 1.557 | -9.50 | 5.700 |