|
Peremennye Zvezdy (Variable Stars) 1, No. 28, 2008 Received 23 November 2007; accepted 20 February 2008.
|
Article in PDF |
The Recent Period Evolution of the RRc stars HY Com, RU Psc and AP Ser
Patrick Wils1
- Vereniging Voor Sterrenkunde, Belgium; e-mail: patrickwils@yahoo.com
| The first overtone RR Lyrae stars HY Com, RU Psc and AP Ser have shown frequent sudden period changes in recent years, as calculated from NSVS and ASAS-3 data. |
1. Introduction
The RRc stars, RR Lyrae stars pulsating in the radial first overtone mode, have been known to show irregular period changes (see e.g. Jurcsik et al., 2001). Rathbun & Smith (1997) found very few RRc stars with large period changes in globular clusters, in contrast to RRab stars. Some Galactic RRc stars have been found to undergo sudden period changes. Since there is good coverage for some of these in the Northern Sky Variability Survey (NSVS; Wozniak et al., 2004) and the All Sky Automated Survey (ASAS-3; Pojmanski et al., 2005), their data can be used to study the recent period history of these stars.
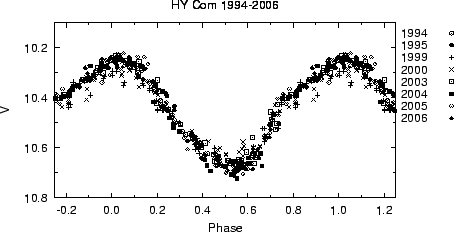
A notable example of an RRc star showing sudden period changes is HY Com (Oja, 1981, 1995). The available ASAS-3 data from 2002 to 2006 are plotted in Fig. 1. The period derived from the 2002-2003 observing season was used for the phase plot in the top left panel. It is clear that this period also reasonably fits the second observing season, but not the later data. To explain the phase diagram the period must have changed at the end of the second observing season. This change must have been quite abrupt as well (significantly less than an observing season) as the period fits two observing seasons, but fails completely for a third. For practical purposes this change in period will be regarded as instantaneous for the remainder of this paper. As will be seen further, the period found for the third season will not fit the data from the final season either, so that another period change must be assumed between these two seasons.
In the following section, a method to model these abrupt period changes is outlined, and then applied to the observations of HY Com. Two other stars, RU Psc and AP Ser, also showing frequent period changes, will be treated as well.
2. Calculation procedure
The procedure used by Wils et al. (2007) to calculate the epoch
and magnitude of a sudden period change was extended to allow for
multiple changes. Epochs ![]() , ...,
, ..., ![]() are chosen at which an
instantaneous period change is assumed, as well as parameters
are chosen at which an
instantaneous period change is assumed, as well as parameters
![]() , ...,
, ..., ![]() representing the fractional frequency change
with respect to the base frequency at those epochs. The times of
observation
representing the fractional frequency change
with respect to the base frequency at those epochs. The times of
observation ![]() are then transformed to a time
are then transformed to a time ![]() which for
which for
![]() is given by
is given by
![]() , for
, for ![]() in
in ![]() , ...,
, ..., ![]() and with
and with ![]() . The value
of
. The value
of ![]() is fixed as the time of the last observation. This
procedure essentially stretches or contracts the time between
period changes so that a single period can be used that is valid
over the entire observation interval. The method further assumes
that the shape of the light curve does not change, and that there
were no phase shifts. With these modified times
is fixed as the time of the last observation. This
procedure essentially stretches or contracts the time between
period changes so that a single period can be used that is valid
over the entire observation interval. The method further assumes
that the shape of the light curve does not change, and that there
were no phase shifts. With these modified times ![]() one can then
proceed as before: in order to find the best values for the
one can then
proceed as before: in order to find the best values for the ![]() parameters
parameters ![]() and
and ![]() , the sum of the squared residuals from
the best fit Fourier series with two harmonics is minimized by
using the downhill simplex minimization method (Nelder & Mead,
1965).
, the sum of the squared residuals from
the best fit Fourier series with two harmonics is minimized by
using the downhill simplex minimization method (Nelder & Mead,
1965).
3. HY Com
The results of the procedure outlined in the previous section applied to the ASAS-3 data for HY Com are shown in Fig. 1. The top right panel shows the phase plot with a single period change near the end of the 2003-2004 season (the data for the final season were not used in the calculation for this specific case). The bottom panel shows the phase plot with two period changes using all the ASAS-3 data for the calculations.
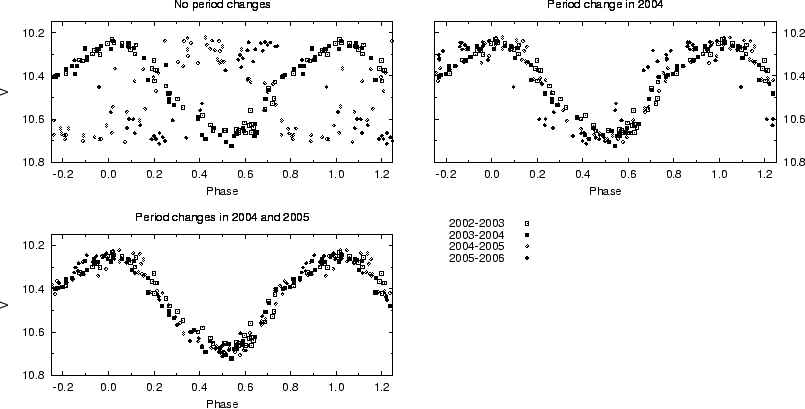 |
Fig. 1. Phase plots of HY Com with ASAS-3 data constructed using the procedure described in the text. The top left panel is a phase plot without period changes, the top right panel has an abrupt period change in 2004, and the bottom panel has an additional period change in 2005. Details for the periods before and after the changes are given in Table 1. |
The calculations were then extended to include the data from NSVS.
The red sensitive NSVS data were adjusted in time by applying the
heliocentric correction and in magnitude by applying a shift to
align them with the average ASAS-3 ![]() magnitude. This revealed
another abrupt period change between the NSVS and ASAS-3 data
sets. Because of the long gap in data between the NSVS data and
the data from Oja (1995) and from Hipparcos (ESA, 1997), no
attempt was undertaken to extend the calculations further in the
past. At least the Oja data for the years 1994 and 1995 do agree
with the earliest derived period. Koen (2001) suggested the
Blazhko effect with a period of 2 years to explain the behaviour
of HY Com from the Hipparcos data. This is however not possible
with the data available now.
magnitude. This revealed
another abrupt period change between the NSVS and ASAS-3 data
sets. Because of the long gap in data between the NSVS data and
the data from Oja (1995) and from Hipparcos (ESA, 1997), no
attempt was undertaken to extend the calculations further in the
past. At least the Oja data for the years 1994 and 1995 do agree
with the earliest derived period. Koen (2001) suggested the
Blazhko effect with a period of 2 years to explain the behaviour
of HY Com from the Hipparcos data. This is however not possible
with the data available now.
Figure 2 gives the final phase plot including all the data from 1994 to 2006 and taking into account three instantaneous period changes. Table 1 lists their details: the time at which they occurred (given as a year including decimals), the sign and magnitude in seconds, a time of maximum useful in an ephemeris, and the new period in days. The first line in the table gives an initial ephemeris to be used before the first calculated period change.
Unfortunately the method used does not allow to easily estimate formal uncertainties on the final results. By changing some of the calculated values and viewing the impact on the phase plot, the precision is likely to be of the order of 10-50 days on the epochs, and a few seconds on the value of the change.
| Year | Change | HJD - | New Period |
| (s) | 2400000 | (d) | |
| - | - | 48762.653 | 0.448615 |
| 2001.39 | -14 | 52050.550 | 0.448447 |
| 2004.32 | +21 | 53123.685 | 0.448694 |
| 2005.66 | -11 | 53611.415 | 0.448564 |
Figure 3 shows the recent period evolution of HY Com on an ![]() plot using a single constant period. The available times of
maximum in this plot from Hübscher (2007) and the TAROT
instrument (Bringer et al., 1999; maxima extracted from the GEOS
RR Lyrae database at http://dbRR.ast.obs-mip.fr, Le Borgne et al.,
2006) were supplemented, for those years with enough data, with
normal maxima determined from the data sources also used above.
This was done by fitting a model curve based on the ASAS-3 data
from 2003 to the observations. Uncertainties on the maxima timings
were plotted when available. For the normal maxima an uncertainty
of 0
plot using a single constant period. The available times of
maximum in this plot from Hübscher (2007) and the TAROT
instrument (Bringer et al., 1999; maxima extracted from the GEOS
RR Lyrae database at http://dbRR.ast.obs-mip.fr, Le Borgne et al.,
2006) were supplemented, for those years with enough data, with
normal maxima determined from the data sources also used above.
This was done by fitting a model curve based on the ASAS-3 data
from 2003 to the observations. Uncertainties on the maxima timings
were plotted when available. For the normal maxima an uncertainty
of 0![]() 01 was assumed. In view of the two most recent maxima
(from TAROT and Hübscher, 2007) in Fig. 3, which date from after
the currently available ASAS-3 data, it is likely that the period
has increased again, less than a year after the last abrupt
change.
01 was assumed. In view of the two most recent maxima
(from TAROT and Hübscher, 2007) in Fig. 3, which date from after
the currently available ASAS-3 data, it is likely that the period
has increased again, less than a year after the last abrupt
change.
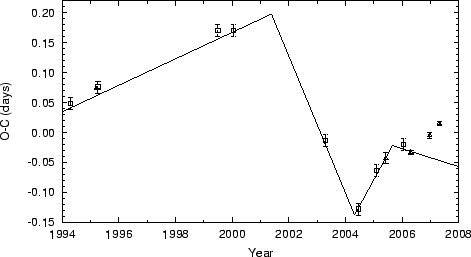 |
Fig. 3.
|
4. RU Psc
RU Psc is another RRc star that has been known to undergo abrupt
period changes (Mendes de Oliveira & Nemec, 1988). The recent
data on RU Psc from the NSVS and ASAS-3 surveys show two abrupt
period changes, separated by only half a year, detailed in
Table 2. Both occurred during the time of the ASAS-3 observations.
Unfortunately not as many observations are available so that the
calculated data are less reliable. For instance, only three data
points were available for 2006, and these do not agree with the
phase plot in Fig. 4 assuming the two period changes. Therefore a
third period change cannot be excluded. This is further confirmed
by recent maxima timings from the GEOS RR Lyrae database, as can
be seen in the ![]() plot in Fig. 5. Although the NSVS data from
1999 seem to fit the period from the earliest ASAS-3 period (until
mid 2003), two maxima reported by Agerer & Hübscher (2002)
likely indicate two more period changes between 1999 and 2002.
plot in Fig. 5. Although the NSVS data from
1999 seem to fit the period from the earliest ASAS-3 period (until
mid 2003), two maxima reported by Agerer & Hübscher (2002)
likely indicate two more period changes between 1999 and 2002.
 |
Fig. 4.
Phase plot of RU Psc using data from
ASAS-3. The upper left panel plots all data with a single period
of 0 |
| Year | Change | HJD - | New Period |
| (s) | 2400000 | (d) | |
| - | - | 51486.610 | 0.390251 |
| 2003.58 | +23 | 52853.659 | 0.390513 |
| 2004.02 | -20 | 53011.816 | 0.390279 |
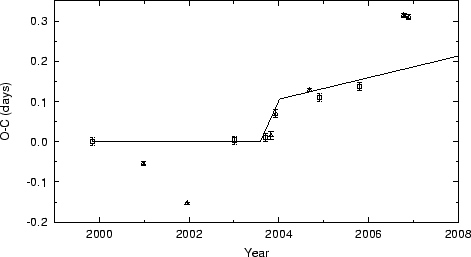 |
Fig. 5.
|
5. AP Ser
The RRc star AP Ser has a known history of period changes as well
(Peña et al., 1990 and Blättler, 2000). Because of the large
gaps with earlier data sets, only the NSVS and ASAS-3 data will be
considered here. Using the method of section 2, three sudden
period changes can be found, with one period change during the
NSVS observation era and two during that of ASAS-3. These are
listed in Table 3. Phase plots are provided in Fig. 6. Since very
few recent maxima timings of AP Ser are available, an ![]() plot
is not given.
plot
is not given.
| Year | Change | HJD - | New Period |
| (s) | 2400000 | (d) | |
| - | - | 51322.722 | 0.340805 |
| 2000.17 | +3 | 51606.607 | 0.340838 |
| 2004.26 | +8 | 53099.479 | 0.340926 |
| 2005.75 | -15 | 53645.643 | 0.340758 |
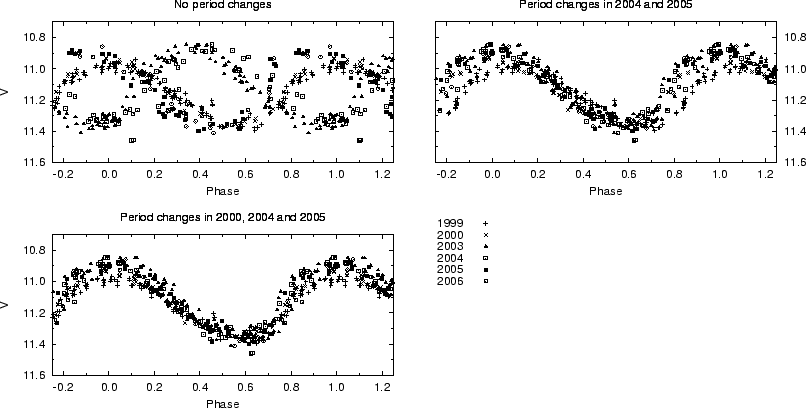 |
Fig. 6.
Phase plot of AP Ser using data from
NSVS (unadjusted red magnitudes) and ASAS-3. The top left panel
plots all data with a single period of 0 |
6. Discussion
It would be very difficult to obtain the above results with the
traditional ![]() method of investigating period changes.
Deviations from a straight line might be attributed to period
noise (Sterne, 1934). This is due in part to the fact that maxima
for an RRc variable are broad. The uncertainty in determining
their exact time, which is often underestimated, may thus hide
small changes in the period. The main reason is however that the
period changes in HY Com, RU Psc and AP Ser are frequent and with
a limited number of maxima timings in between changes it would be
hard to obtain a reliable period. This is especially so if these
maxima times are determined from survey data such as from NSVS and
ASAS-3, because there will not be enough data available to
accurately calculate two times of maximum between period changes.
Essentially, good coverage of the star in phase as well as in time
is needed.
method of investigating period changes.
Deviations from a straight line might be attributed to period
noise (Sterne, 1934). This is due in part to the fact that maxima
for an RRc variable are broad. The uncertainty in determining
their exact time, which is often underestimated, may thus hide
small changes in the period. The main reason is however that the
period changes in HY Com, RU Psc and AP Ser are frequent and with
a limited number of maxima timings in between changes it would be
hard to obtain a reliable period. This is especially so if these
maxima times are determined from survey data such as from NSVS and
ASAS-3, because there will not be enough data available to
accurately calculate two times of maximum between period changes.
Essentially, good coverage of the star in phase as well as in time
is needed.
It is interesting to note that the values of the period changes in
Tables 1 to 3 are of the same order (although they are not exactly
the same) and that subsequent period changes have opposite signs
in almost all cases. Such a behaviour can be explained by discrete
mixing events in the semiconvective zone inside the star, as
proposed by Sweigart and Renzini (1979). The magnitude of the
observed changes, ![]() of the order of
of the order of ![]() on average, is consistent with their theoretical models. However
the observed time scale between changes is not. Sweigart and
Renzini found an average time scale of a few centuries overall,
and specifically of about a century when the star is near the end
of its core helium burning phase, whilst the RRc stars discussed
in this paper appear to show abrupt period changes once every few
years. Belserene (1978) already noted that the observed time scale
between these events for the RRab star IV Cyg is much shorter as
well. Sweigart and Renzini indicated however that the observed
quantities likely depend significantly on the model parameters,
while they only studied a limited number of models in detail.
on average, is consistent with their theoretical models. However
the observed time scale between changes is not. Sweigart and
Renzini found an average time scale of a few centuries overall,
and specifically of about a century when the star is near the end
of its core helium burning phase, whilst the RRc stars discussed
in this paper appear to show abrupt period changes once every few
years. Belserene (1978) already noted that the observed time scale
between these events for the RRab star IV Cyg is much shorter as
well. Sweigart and Renzini indicated however that the observed
quantities likely depend significantly on the model parameters,
while they only studied a limited number of models in detail.
Clearly further theoretical investigation is necessary to fully explain the observed behaviour of the three RRc stars above, and possible other stars of the type. Also in order to be sure of the real timescale in which these period changes take place, regular, almost continuous monitoring of the full light curve of these stars is necessary.
Acknowledgements: I would like to thank Sebastián Otero for drawing my attention to HY Com and AP Ser, Horace Smith for directing me to the relevant theoretical work on period changes in RR Lyrae stars, and John Greaves for useful comments. This research has made use of NASA's Astrophysics Data System, the SIMBAD and VizieR databases operated at the Centre de Données Astronomiques, and the GEOS RR Lyrae web database.
References:
Agerer, F., Hübscher, J., 2002, IBVS, No. 5296
Belserene, E.P., 1978, Journal of the AAVSO, 7, 76
Blättler, E., 2000, IBVS, No. 4954
Bringer, M., Boër M., Peignot, C., et al., 1999, A&A Suppl., 138, 581
ESA, 1997, The Hipparcos and Tycho Catalogues, ESA SP-1200
Jurcsik, J., Clement, C., Geyer, E.H., Domsa, I., 2001, AJ, 121, 951
Koen, C., 2001, MNRAS, 321, 44
Hübscher, J., 2007, IBVS, No. 5802
Le Borgne, J.F, Klotz, A., Boër, M., 2006, IBVS, No. 5717
Mendes de Oliveira, C., Nemec, J.M., 1988, PASP, 100, 217
Nelder, J.A., Mead, R., 1965, Computer Journal, 7, 308
Oja, T., 1981, A&A, 103, 339
Oja, T., 1995, IBVS, No. 4276
Peña, J.H., Díaz, L.M., Peniche, R., 1990, Rev. Mex. Astron. Astrofis., 20, 139
Pojmanski, G., Pilecki, B., Szczygie![]() , D., 2005, Acta
Astron., 55, 275
, D., 2005, Acta
Astron., 55, 275
Rathbun, P., Smith, H., 1997, PASP, 109, 1128
Sterne, T.E., 1934, Harvard College Observatory Circular, 386, 1
Sweigart, A.V., Renzini, A., 1979, A&A, 71, 66
Wils, P., Otero, S.A., Hambsch, F.-J., 2007, IBVS, No. 5765
Wozniak, P.R., Vestrand, W.T., Akerlof, C.W., et al., 2004, AJ, 127, 2436