 << A.1 Матричная алгебра
| Оглавление |
A.3 Декартовы прямоугольные и >>
<< A.1 Матричная алгебра
| Оглавление |
A.3 Декартовы прямоугольные и >>
Система линейных уравнений
эквивалентна матричному уравнению
Если матрица
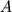
не вырождена, то матричное уравнение имеет
единственное решение:
Если матрица 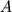 является ортогональной и ее детерминант равен
единице
является ортогональной и ее детерминант равен
единице
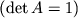 , то линейное преобразование
, то линейное преобразование 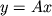 называется вращением.
называется вращением.
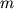 уравнений
уравнений
линейно независимы, если из условия
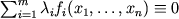
при всех значениях
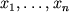
следует, что
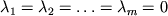
. В
противном случае эти
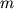
уравнений линейно зависимы, т.е. по
крайней мере одно из уравнений может быть представлено в виде
линейной комбинации остальных.
Векторы
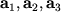 линейно
независимы, если из уравнения
линейно
независимы, если из уравнения
следует, что
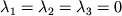
. В противном
случае векторы
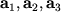
линейно
зависимы и по крайней мере один из них, например,
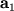
может быть выражен в виде линейной комбинации
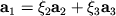
остальных векторов.
В трехмерном пространстве каждое множество трех линейно
независимых векторов является базисом.
Любой вектор
 в трехмерном пространстве может быть
представлен в виде разложения:
в трехмерном пространстве может быть
представлен в виде разложения:
относительно базисных векторов
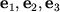
. В трехмерном пространстве числа
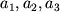
являются
координатами вектора

в системе координат, определяемых
базисными векторами
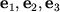
.
<< A.1 Матричная алгебра
| Оглавление |
A.3 Декартовы прямоугольные и >>

![]() является ортогональной и ее детерминант равен
единице
является ортогональной и ее детерминант равен
единице
![]() , то линейное преобразование
, то линейное преобразование ![]() называется вращением.
называется вращением.
![]() уравнений
уравнений
![]() линейно
независимы, если из уравнения
линейно
независимы, если из уравнения
![]() в трехмерном пространстве может быть
представлен в виде разложения:
в трехмерном пространстве может быть
представлен в виде разложения: