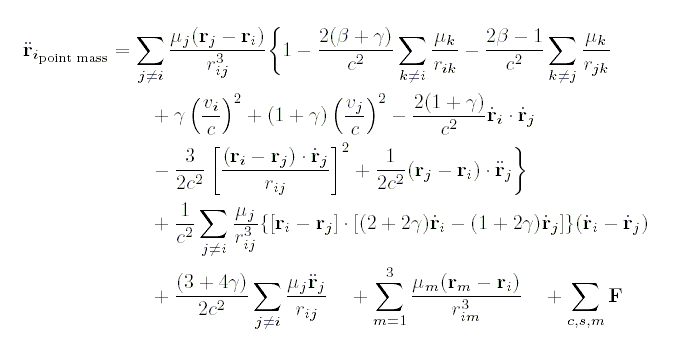args[0]=message
args[1]=DB::DB::Message=HASH(0x1740b60)
Re[7]: Смещение перигелия Меркурия и других планет
11.12.2013 17:42 | С. Ю. Юдин
| Цитата: |
| Юдин, я бы сидел и помалкивал, но: Эллиптическая орбита Меркурия забрасывается в сторону вращения Солнца по причине опережающих приливных горбов Солнца. Полная аналогия забрасывания Луны приливными горбами Земли. Плохо, когда астрономы плохо знают теормех. |
- Смещение перигелия Меркурия и других планет
(С. Ю. Юдин,
18.11.2007 9:08, 411 Байт, ответов: 127)
Я уже пробовал открыть эту тему на этом форуме, но тогда у меня возникли проблемы с кодировкой и текст оказался не читаемым. Сейчас попробую другой вариант кодировки, т.к. исследования не только дали очень интересные результаты, но и поставили передо мною много новых вопросов на которые я сам не могу дать ответ и по этому требуется помощь астрономов.
С наилучшими пожеланиями Сергей Юдин.
- Re: Смещение перигелия Меркурия и других планет
(С. Ю. Юдин,
18.11.2007 9:13, 10.9 КБайт, ответов: 42)
После того, как Леверье в середине 19 века обработал данные наблюдений за Меркурием у него получилось, что его перигелий как бы поворачивается по ходу движения планеты на 565,1 угловой секунды за 100 лет (за вычетом угла поворота системы отсчета, т.е. прецессии), а по расчетам, т.е. с использованием законов Ньютона, должно было быть 526,83 и получилось, что 38,27 секунды не объясняются теорией Ньютона и, следовательно, являются аномальным остатком, который требует своего объяснения другими теориями или введением новых объектов в состав Солнечной системы. После этого и начался активный поиск планеты Вулкан, расположенной между Солнцем и Меркурием, и изобретение новых теорий тяготения.
В конце 19 века Ньюком тоже занялся этим вопросом и получил в 1882 г. смещение 42,95 секунды. После этого он тоже, как и Леверье, стал создавать так называемые теории движения Меркурия, Венеры, Земли и Марса. И после обработки экспериментальных данных с массами планет, отличными от масс планет использованных Леверье, получил расхождение между наблюдаемыми значениями изменения во времени 4-х параметров (перигелий, угол восхождения, угол наклона и эксцентриситет) и расчетными, т.е. получающимися по теории Ньютона. Его данные по перигелиям планет я привожу ниже, а также даю результаты, которые дают различные теории, отличающиеся от теории Ньютона, по объяснению этого аномального остатка и привожу результаты, полученные по теории Зеелингера, который объяснил аномальное смещение, полученное Ньюкомом полностью в рамках теории Ньютона. Таким образом для этой теории не совсем корректно говорить об остатке как об аномальном, т.е. не описывающимся теорией Ньютона. А конкретно Зеелингер учел в расчетах смещение, которое может быть вызвано космической пылью и мелкими астероидами, которые создают так называемое зодиакальное свечение, которое астрономы наблюдают, но определить параметры этих поясов пыли не могут. По этому Зеелингер просто подобрал параметры двух поясов пыли, чтобы объяснить почти все аномалии Ньюкома (в том числе и смещение узлов Венеры).Таблица 2-Ньюком. Обработанные экспериментальные данные смещения перигелиев 4-х планет и аномальные остатки этого смещения, полученные Ньюкомом, которые не объясняются теорией Ньютона, но объясняются другими теориями в дополнение к смещению, объясненному теорией Ньютона (в скобках указан источник откуда взяты данные по теориям объясняющим аномальный остаток).
_________________________Меркурий__Венера___Земля___Марс
Чистый поворот перигелия_____575,1____42,5____1162,9__1602,7
Объясняется теорией Ньютона__533,8____49,9____1156,9__1594,7
Остаток для других теорий______41,2____-7,3______6,0_____8,0
Эйнштейн (Субботин)__________43,0_____8,6______3,8_____1,4
Гербер (Хайдаров)_____________43,0_____8,6______3,8_____1,4
Ритц (Роузвер)________________41,0_____8,0______3,4_____----
Мах (Зайцев)_________________43,0_____23,0_____17,0____11,0
Зеелингер (Роузвер)___________41,3______7,3______4,2_____6,3А год назад к этому процессу подключился и я, но не за тем, чтобы изобретать свою новую теорию, а для того, чтобы на этом классическом примере продемонстрировать возможности математического моделирования систем в решение этого вопроса, т.к. я являюсь специалистом именно по моделированию систем и оптимизации их параметров. Т.к. сама математическая модель (плоская) Солнечной системы у меня уже давно была переделана под Windows (программа Solsys2), то мне предстояло только ее переделать для расчета смещения перигелиев планет, что я и сделал в 3-ей версии программы, которая показала удовлетворительные данные по определению смещения перигелиев планет, но дисперсия полученных данных была очень велика. После этого я в 4-ой версии сосредоточил свое внимание именно на различных методах статистической обработки данных и добился очень хороших результатов. А кроме этого я переделал модель в трехмерную дополнил программу определением расчетных значений смещений других параметров орбит планет и множеством других полезных функций.
Как показали полученные мною на программе Solsys4 результаты по определению вековых смещениев параметров орбит планет Солнечной системы (перигелия, наклона, эксцентриситета и узла восхождения), применяемая сейчас в астрономии методика по определению этих величин нуждается в серьезной корректировке. Хотя сразу хочу предупредить, что полученные мною данные очень сырые и обязательно будут уточняться (но не изменяться кардинально), т.к. я не только постоянно модернизировал по ходу проведения экспериментов методику статистической обработки данных, но и не оптимизировал период одного цикла статистической обработки во время проведения вычислительных экспериментов и вносил мелкие корректировки в код программы, а это все влияет на полученный конечный результат. Посмотрите пожалуйста на скриншот программы Solsys4, при определение вековых смещений для Сатурна
http://ser.t-k.ru/Ris/Saturn.gif
Здесь явно просматривается цикличность изменения смещения перигелия Сатурна при каждом новом обороте (пролете) от некоторого среднего значения (немного дрейфующего в сторону увеличения) под влиянием движения Солнца и Юпитера. На графике это точки рассчитанные как смещение перигелия от начала эксперимента, пересчитанное в смещение за 100 лет. Если мы обработаем по существующей методике данные наблюдений за период времени Т1, то получим значение смещения перигелия Р1, а если обработаем данные наблюдений за период времени Т2, то получим значение смещения перигелия Р2. И только в том случае, если мы обработаем данные за период Т3 (в приведенном примере Т3=1178 лет), то мы получим правильное значение векового смещения перигелия и то только в том случае, если у нас нет дрейфа, т.е. вековое смещение остается примерно одинаковым на протяжение нескольких столетий или тысячелетий в зависимости от продолжительности периода колебаний параметра (для внутренних планет этот период не большой). А, как видно из графика, для Сатурна мы имеем явный дрейф, т.к. со временем смещение растет, и по этому, даже полученное за период Т3, значение векового смещения перигелия справедливо только в этом интервале времени. По этому я в своей программе Solsys4 применил статистическую обработку данных наблюдений по циклам, где количество наблюдений берется равным оборотам планеты за период времени Т3, а не так как это было в программе Solsys3, когда вычислялось среднее значение по всем пролетам от начала эксперимента. Но и здесь все оказалось не так просто.
Даже при циклическом расчете (данные по первой методике серые кружки и черточки и по второй методике белые кружки и черточки) результаты получаются несколько разные, но самое главное это то, что по 2-ой методике получается очень маленькая дисперсия по сравнению с 1-ой методикой. На графике кружки это значения в данном цикле расчета, а черточки это матожидание по всем циклам расчета. В программе Solsys4 я оставил расчет по обеим методикам только по перигелию (для сравнения методик), а по смещению угла наклона орбиты (зеленые кружки и черточки) и угла узла восхождения (красные), а также эксцентриситета орбиты (синие) применяется только 2-я методика. Но при наличие дрейфа, когда смещение монотонно увеличивается (перигелий у Сатурна) или уменьшается (угол наклона орбиты у Сатурна) по линейной или квадратичной зависимости, требуется уже совсем другая методика статистической обработки данных полученных по результатам циклической обработки, т.е. надо применять или линейную или квадратичную аппроксимацию, т.к., полученное при обычной статистической обработке данных (используется сейчас в программе), правильное среднее значение этих величин получается только для конкретного момента времени и то только при линейном дрейфе.
А к чему приводит неправильная методика обработки экспериментальных данных наблюдений мы сейчас рассмотрим на примере Венеры. Смотрите скриншот программы при проведении вычислительного эксперимента с Венерой
http://ser.t-k.ru/Ris/Venera.gif
Здесь явно видно, что изменение эксцентриситета (синие кружки и черточки) и смещение узла восхождения (красные кружки и черточки) за 100 лет практически не изменяется на протяжении всего эксперимента, т.е. 5000 лет, а смещение перигелия и узлов восхождения монотонно изменяется и по этому, определенное по экспериментальным данным за один промежуток времени, оно не будет равно смещению за другой промежуток времени. Например, среднее значение смещения, рассчитанное при обработке экспериментальных данных вычислительного эксперимента с 1700 по 1900 год (примерно равно интервалу, который использовал Ньюком), у нас получится равным 20 секундам в 1800 году. А при обработке данных, например, с 1995 по 2005 год у нас получится равным минус 5 секунд в 2000 году. Я считаю, что не в последнюю очередь именно этим объясняется такое расхождение в экспериментальных данных различных авторов, которое я даю в таблице 4, где я привожу и свои расчетные данные для разных эпох (особенно наглядно видно различие в данных Ньюкома, Данкома и НАСА по Венере).Таблица 4. Обработанные экспериментальные данные наблюдений по смещению перигелиев 6-и планет разных авторов (без указания эпох) и мои расчетные данные для разных эпох (в скобках указан источник откуда взяты данные).
______________Меркурий__Венера__Земля_Марс__Юпитер_Сатурн
Юдин 1800_________529,2___20,0__1136____1602__738_____2012
Юдин 2000_________529,2___-5,0__1137____1602__748_____2027
Ньюком (Роузвер)___575,1___42,5__1162,9__1602,7____-________-
Данком (Брумберг)__575,2___34,3__1153,8____-_______-________-
НАСА (Хайдаров)__573,57__-108,8_1198,3__1560,8__839,9_-1948,9
Брауэр, Вурком ____589,1_____-_____-_____1800,0__432,0_2757,5
(Субботин)Таким образом как методику обработки экспериментальных данных, так и методику определения расчетных значений, применяемые сейчас астрономами в предположение, что вековые смещения по углу перигелиев, восходящих узлов и наклонов орбит, а также их эксцентриситетов остаются неизменными, необходимо менять. Тем более, что и сами эксцентриситеты и углы наклона входящие в формулы определения смещениев перигелия и узла восхождения как константы тоже меняются во времени. Таким образом, если обработать первичные данные наблюдений за планетами по моей методике (или хотя бы усовершенствовать стандарную методику обработки данных наблюдений с разбиением данных на циклы), то мы должны получить не какие то константы, а уравнения регрессии для наблюдаемых и теоретических значений аналогичные тем, что получил Ньюком в своей //теории// планет, где он для всех параметров орбит в функции времени получил степенные зависимости (вплоть до 3-ей степени). И только после этого можно будет определить аномальные остатки (опять таки в функции времени) и делать какие то выводы о справедливости той или иной теории объясняющей эти остатки.
С наилучшими пожеланиями Сергей Юдин. - Re[2]: Смещение перигелия Меркурия и других планет
(С. Ю. Юдин,
18.11.2007 9:16, 4.4 КБайт, ответов: 41)
(продолжение)
А сейчас я дам предварительные данные по проверке одной из гипотез объясняющей эти аномальные отклонения (которые получены пока на основе имеющихся методик обработки данных) во время которой у меня и возник вопрос к астрономам (а может быть и астрофизикам). Конкретно я проверял гипотезу о конечности скорости распространения гравитации, когда сила притяжения от 1-ой планеты действует на 2-ю планету не из той точки, где 1-я планета находится сейчас, а из той точки, где 1-я планета находилась несколько минут назад, необходимых для того, чтобы гравитационное поле преодолело это расстояние между планетами. Только не надо путать эту гипотезу с гипотезой Гербера, который этот эффект не учитывал, а учитывал как бы динамическое давление создаваемое гравитационным полем в дополнение к статическому давлению, рассчитываемому по закону Ньютона, по аналогии с давлением ветра в паруса корабля дующим по ходу движения корабля и против его движения.
Так вот, когда я стал проверять эту гипотезу на своей модели Солнечной системы, то выяснилось, что в покоящейся системе даже скорость гравитации равная 1% от скорости света практически не оказывает никакого влияния на вековые смещения параметров орбит планет (при большей скорости влияние будет еще меньше). Но, когда я задал поступательную скорость всей Солнечной системе 20 км/с и скорость распространения гравитации равную скорости света, то эффект оказался даже больше, чем я мог предположить и смещение перигелия происходит при разных направлениях движения Солнечной системы, как в сторону увеличения, так и в сторону уменьшения. Таким образом, очевидно можно подобрать такую скорость системы при заданной скорости гравитации, когда будет получен нужный результат, но это будет уже гадание на кофейной гуще, т.к. во-первых результат будет зависеть от заданной скорости гравитации (чему она равна никто сейчас не знает), а во-вторых будут заранее отсечены все другие гипотезы, например, с тем же динамическим давлением Гербера и по этому результат то мы получим, но законы Природы не познаем.
В связи с этим я прошу астрономов немного сузить область допустимых решений, т.е. помочь мне хотя бы определить чему равна абсолютная скорость движения Солнечной системы (а может быть относительная, если //эфир//, который нужен для распространения гравитации, движется вместе с нашей галактикой) и куда система движется в эклиптических координатах, а может быть и помочь с определением скорости распространения гравитации. Из литературных источников известно, что скорость Солнечной системы относительно ближайших звезд равна 20 км/с и движется она в направлении апекса - точки на небесной сфере с координатами прямое восхождение 270 град, склонение 30 град, а по отношению к другим, более далеким звездам, Солнце движется немного быстрее и изменяет направление в сторону большего прямого восхождения. Но есть также данные о том, что апекс Солнца расположен с прямым восхождение 258 град и склонением минус 17 град, а скорость равна 22-25 км/с, если определять движение относительно межзвездного газа. Так вот я во-первых не понял как эти координаты (которые, наверное, даны в экваториальной системе координат), перевести в эклиптические, а во-вторых какие из этих данных сейчас считаются более достоверными.Но и это еще не все. Из других литературных источников я узнаю, что Солнце вращается относительно центра нашей галактики с угловой скоростью 0,0053 сек/год по радиусу 10 кпк, что дает линейную скорость 251 км/с. Хотя есть и другие похожие данные, что Солнце вращается с угловой скоростью 0,006972 сек/год по радиусу 16,5*10^8 а.е., что дает линейную скорость 268 км/с. Вот только я ничего не нашел относительно того, где же он находится этот центр галактики, т.е. направление на него в эклиптической системе координат на сегодняшний день, чтобы определить направление движения Солнца. А кроме того, как я догадываюсь, наверное и сама наша галактика куда-то летит и с какой-то скоростью. Буду очень признателен, если Вы мне поможете разобраться с вопросом - чему же равна абсолютная скорость Солнца (а может быть нужна относительная, т.е. относительно //эфира//, если он движется вместе с галактикой) и куда она в эклиптических координатах в эпоху 1900 направлена. Наверное, я задал слишком сложные вопросы и никто на них однозначно ответить не сможет, но я буду признателен даже за мелкие пояснения.
С наилучшими пожеланиями Сергей Юдин. - Re[3]: Смещение перигелия Меркурия и других планет
(В. В. Чазов,
24.11.2007 13:08, 556 Байт, ответов: 40)
Здравствуйте, уважаемый Сергей. Следил за дискуссией на "мембране", потому чуть-чуть в
курсе Ваших замечательных исследований.
Ваши вопросы о движении Солнца вполне конкретные, постараюсь найти ответ и напишу его через некоторое время. В этом буду, очевидно, не одинок, на нашем форуме первоклассные специалисты.
О Ваших исследованиях надо размышлять.
Сергей, можете ли Вы согласиться с тем, что астрономы обрабатывают первичные наблюдения совершенно по другой схеме, чем та, которую моделируете Вы?
С поклоном, Вадим. - Re[4]: Смещение перигелия Меркурия и других планет
(В. В. Чазов,
24.11.2007 17:47, 1.3 КБайт, ответов: 8)
Дорогие друзья, уважаемый Сергей.
Про апекс движения Солнца.
Все числа в Вашей статье правильные: и относительно ближайших звёзд, и относительно межзвёздного газа, и скорость относительно центра Галактики. В эклиптических координатах направление на апекс движения Солнца равно приблизительно 270 градусов эклиптической долготы и +53 градуса 24 минуты эклиптической широты.
Про центр Галактики.
Эклиптические координаты центра Галактики составляют приблизительно 267 градусов эклиптической долготы и минус(-)(5 градусов 32 минуты) эклиптической широты.
Уважаемый Сергей, Вам интересен именно процесс моделирования, это замечательно. Но тогда конкретные числа Вам совсем не нужны. Если кто-либо посоветует Вам сравнить результаты Ваших моделей с действительным положением вещей в Солнечной системе - не слушайте его. Любое сравнение потребует вывода правильных уравнений движения небесных тел, тщательного программирования и нахождения начальных условий для решения задачи Коши методом численного интегрирования. Затратив много усилий, можно в лучшем случае лишь приблизиться к современным научным результатам, то есть моделям движения планет, которые недёжно обеспечивают все космические миссии.
С поклоном, Вадим. - Re[5]: Смещение перигелия Меркурия и других планет
(С. Ю. Юдин,
25.11.2007 16:52, 1.5 КБайт, ответов: 7)
< tbody>
Цитата:
Уважаемый Сергей, Вам интере сен именно процесс моделирования, это з амечательно. Но тогда конкретные числа Вам совсем не нужны. Если кто-либо посоветует В ам сравнить результаты Ваших моделей с действительным положением вещей в Солнечной с истеме - не слушайте его. Любое сравнение потребует вывода правильных уравнений движ ения небесных тел, тщательного программирования и нахож дения начальных условий дл я решения задачи Коши методом численного интегрирования. Затратив много усилий, мож но в лучшем случае лишь приблизиться к современным научным результатам, то есть мо делям движения планет, которые недёжно обеспечивают все космические миссии.А вот здесь не все так однозначно.
Во-первых мне интерес ен не столько процесс моделирования, сколько результаты, которые созданные мною модели позв оляют получить. Другое дело, что сейчас моделями называют и квазимодели и вообще имитаторы, т.е. симуляторы (симулянты) и по этому я пытаюсь донести до всех важность создания именно мо делей для познания природы и общества. При этом хочу заметить, что создание полноценных моделей (даже не очень сложных систем) стало возможно только с изобретением компьютеров (и не только для численного решения дифференциальных уравнений).А во-вторы х результ аты выч
- Re[6]: Смещение перигелия Меркурия и других планет
(С. Ю. Юдин,
25.11.2007 16:54, 1.4 КБайт, ответов: 6)
А во-вторых результаты вычислительных экспериментов необходимо сравнивать именно с // действительным положением вещей в Солнечной системе //, т.к. модели это копии именно реальных объектов, а не каких-то других моделей или имитаторов. И потом, я очень сомневаюсь, что все эти модели, которые, как Вы пишите // недёжно обеспечивают все космические миссии // являются именно моделями. Да по поводу надежности космических миссий у меня несколько иная точка зрения, т.к. по моим данным многие космические аппараты улетели не совсем туда, куда они должны были лететь по данным полученным на этих моделях.
А в-третьих я сейчас заканчиваю описание программы Solsys4, чтобы каждый мог сам провести на ней несколько вычислительных экспериментов и убедиться насколько она достоверно описывает объективную реальность. И, чтобы добиться большей адекватности своей модели реальной системе, я продолжаю ее совершенствовать и скоро приступлю к 5-ой версии.
И наконец в-четвертых. Я не понял чему же равно расстояние до центра галактики и чему равна скорость Солнца, т.к. я приводил разные данные (какие из них точнее или это нельзя определить), и потом Вы дали координаты апекса Солнца именно относительно центра галактики ?.
А также, Что Вы думаете о данных полученных COBE и WMAP по исследованию реликтового излучения и как соотносятся эти данные (опять таки в эклитических координатах) с теми, что привели Вы.С наилучшими пожеланиями Сергей Юдин.
- Re[7]: Смещение перигелия Меркурия и других планет
(В. В. Чазов,
25.11.2007 21:23, 1.1 КБайт, ответов: 5)
Здравствуйте, дорогие друзья, здравствуйте, Сергей.
Продолжаю надеяться на помощь специалистов. Локальные и интегральные характеристики важны для сложных моделей: прогноз погоды, выборы конгрессменов, биржа бездельников. Модель движения планет Солнечной системы относительно барицентра совсем проста: шесть дифференциальных уравнений и шесть значений начальных условий для каждой планеты, Солнца и Луны плюс параметры альфа, бета и гамма для оценки эффектов, порождаемых отличием закона тяготения от красивого закона обратной пропорциональности квадратам расстояний.
Оценка расстояния от центра Галактики до Солнечной системы равна 2.7e+18 km.
Эклиптические координаты апекса движения Солнца даны в системе отсчёта с началом в центре Солнца.
Любые оценки являются очень приближёнными. Оценки в системе различных объектов различаются между собой.
О данных COBE и WMAP ничего не знаю.
Сергей, приветствую Ваши фатастические исследования. Мне в этой жизни путешествовать в пространстве-времени Солнечной системы гораздо проще: помогают эфемериды движения планет и Луны.
С поклоном, Вадим. - Re[8]: Смещение перигелия Меркурия и других планет (В. В. Чазов, 25.11.2007 21:27, 152 Байт, ответов: 4) Простите великодушно. Оценка расстояния от центра Галактики до Солнечной системы равна 2.7e+17 km. Но что это меняет? Желаю всем немного удачи. Вадим.
- Re[9]: Смещение перигелия Меркурия и других планет (Т. Г. Архангельский, 27.11.2007 10:28, 6 Байт)
- Re[9]: Смещение перигелия Меркурия и других планет (А. Н. Егоров, 17.11.2008 14:08, 385 Байт, ответов: 2) Надеюсь тема еще не заглохла. Не совсем уяснил. У Венеры перигелий смещается в другую сторону от предсказаний ОТО? По таблице как я понял, величина смещения примерно совпадает, но со знаком минус. Где можно найти ссылку на эти данные? Мне нужно будет сослаться на это в диссертации, а самостоятельно никаких официальных данных я не нашел, чтоб в журнале типа УФН, или еще где.
- Re[10]: Смещение перигелия Меркурия и других планет
(Карим Хайдаров,
19.11.2008 17:11, 811 Байт)
- Есть классическая книга Роузвера Перигелий Меркурия от Леверье до Эйнштейна" Вообще всё есть на сайте NASA. Точные обсерваторные данные. Я брал оттуда.Цитата: Надеюсь тема еще не заглохла. Не совсем уяснил. У Венеры перигелий смещается в другую сторону от предсказаний ОТО? По таблице как я понял, величина смещения примерно совпадает, но со знаком минус. Где можно найти ссылку на эти данные? Мне нужно будет сослаться на это в диссертации, а самостоятельно никаких официальных данных я не нашел, чтоб в журнале типа УФН, или еще где. - Re[10]: Смещение перигелия Меркурия и других планет
(С. Ю. Юдин,
1.12.2008 21:41, 865 Байт)
Цитата: Надеюсь тема еще не заглохла. Заглохла или нет тема я не знаю, но свои исследования по этому вопросу я продолжаю. Правда именно по методике обработке первичных данных наблюдений мне что-то никто не пишет. Вот сейчас на Астрофоруме опять забросали меня чисто теоретическими вопросами, которые я не хочу обсуждать до тех пор пока не получу надежных наблюдательных данных по параметрам орбит. Так, что можете сходить вот сюда http://www.astronomy.ru/fo rum/index.php/topic,46843.60.html , если интересуетесь теоретическими вопросами.
С наилучшими пожеланиями Сергей Юдин. - Re[4]: Смещение перигелия Меркурия и других планет
(С. Ю. Юдин,
25.11.2007 16:45, 744 Байт, ответов: 1)
Здравствуйте Вадим.
Во-первых спасибо за помощь, а во-вторых я постараюсь ответит ь на ваши вопросы и задам новые.
Цит ата: Сергей, можете ли Вы согласиться с т ем, что астрономы обрабатывают первичные наблюдения совершенно по другой схеме, чем та, которую моделируете Вы? Я не только со гласен с этим, но и настаиваю на том, чтобы астрономы откорректировали свою методику так, чтобы смещение получалось не интегральным по всем экспериментальным данным за весь период на блюдений, как константа, а в виде фу нкции (кв адратич
- Re[5]: Смещение перигелия Меркурия и других планет
(С. Ю. Юдин,
25.11.2007 16:49, 1.2 КБайт)
(опять какие то проблемы с сообщениями - повторяю ответ)
Я не только согласен с этим, но и настаиваю на том, чтобы астрономы откорректировали свою методику так, чтобы смещение получалось не интегральным по всем экспериментальным данным за весь период наблюдений, как константа, а в виде функции (квадратичной аппроксимации)
Смещение=k0+k1*T+k2*T^2
Но быстрее всего мне наверное самому придется заняться созданием этой методики, т.к. времени ждать, когда это произойдет, у меня нет.
И маленькое замечание, по поводу Вашей фразы // по другой схеме, чем та, которую моделируете Вы //, которая мне, как специалисту по моделированию режет слух.
Схему, также как и план, методику, алгоритм и т.д. смоделировать нельзя. Ее можно (уже существующую, например, для нахождения корней квадратного уравнения) только перевести с языка математики на машинный язык (не обязательно напрямую, т.к. это очень сложно, а можно сначала на какой нибудь язык программирования, а потом в машинные коды).
А смоделировать можно только какую нибудь систему (механическую, биологическую, социально-экономическую и т.д.), но для того, чтобы это сделать, надо знать хотя бы азы моделирования систем.
С наилучшими пожеланиями Сергей Юдин.
- Re[4]: Смещение перигелия Меркурия и других планет
(Т. Г. Архангельский,
27.11.2007 10:46, 754 Байт, ответов: 28)

Уважаемый Сергей!
Мною разработано новое мировоззрение - ГАЛАЦЕНТРИЧЕСКО- с движением Светила и с ним Солнечной системы по нашей ГАЛАКТИКЕ.
При научной работе вычислена скорость движения Солнца в пределах Солнечной ситемы.
Это - первая часть работы. Она имеется на сайте Московского астроклуба, других и меет свой адрес
http://gala-astronomia.com.
Прошу ознакомиться.
Во втораой части работы - обоснована, думается, объективная причина смещения перигелия Меркурия. Но она есще нигде не размещена.
Если Вам что-либо будет интересно в научном сообщении, будут вопросы и предложения - пишите
kvg013@mail.utech.ru.
Тарас Архангельский.
- Re[5]: Смещение перигелия Меркурия и других планет
(С. Ю. Юдин,
28.11.2007 18:15, 1.4 КБайт, ответов: 27)
< tbody>
Цитата: 
Если Вам что-либо будет интересно в научном сообщении, бу дут вопросы и предложения - пишитеЗа стремление мне помочь, конечно же спасибо, но никакие вопросы по Вашей работе я задават ь не буду (с меня хватит и того, что я прочитал). Хотя стремление внести в науку что то новое я всегда при ветствую.
Астронет | Научная сеть | ГАИШ МГУ | Поиск по МГУ | О проекте | Авторам Комментарии, вопросы? Пишите: info@astronet.ru или сюда ния - пишите
С наилучшими пожеланиями Сергей Юдин.
kvg013@mail.utech.ru.
Тарас Архангельский. r />
- Re[6]: Смещение перигелия Меркурия и других планет
(С. Ю. Юдин,
6.12.2007 14:35, 3.1 КБайт, ответов: 26)
К сожалению, приведенные в литературных источниках данные по скорости Солнечной системы оказались очень противоречивые и не только по величинам различных относительных скоростей и абсолютной, но и по их направлениям. По этому для прояснения этого вопроса нужны дополнительные исследования и я этим займусь при создание 5-й версии программы Solsys. Кроме того, как я писал выше, и, полученные астрономами после обработки данных наблюдений, экспериментальные данные по вековым изменениям параметров орбит планет тоже требуют серьезных уточнений для чего необходимо для обработки первичных данных применить мою методику, использованную в программе Solsys4 для обработки данных полученных при проведение вычислительных экспериментов. По этому, я пока выложил на своей домашней странице ( http://ser.t-k.ru/ и на зеркале http://modsys.narod.ru/ ) окончательный вариант программы Solsys4, чтобы каждый смог сам проверить полученные мною экспериментальные данные и сделать по ним собственные выводы и сравнить их с выводами сделанными мною
1- Применяемая сейчас (и раньше) астрономами методика обработки данных первичных наблюдений за планетами с целью определить постоянные параметры орбит планет и их периодические и вековые изменения, основанная на теории возмущений, нуждается в серьезной корректировке. И конкретно по вековым смещениям параметров орбит она должна позволять получать не одно число dP0, а выражение вида dP100=dP0 + k1 * T + k2 * T^2, где k1,k2 коэффициенты, а T время, что, например, по перигелию очень актуально для Венеры.
2- До тех пор пока данные наблюдений не будут заново обработаны по новой методике, говорить об аномальных остатках, т.е. величинах смещений не объясняемых теорией Ньютона преждевременно (хотя быстрее всего по Меркурию аномальный остаток смещения перигелия примерно таким как сейчас и получится). И таким образом, говорить и об экспериментальном подтверждение общей теории относительности или любой другой, дающих в дополнение к смещению, полученному по законам Ньютона с мгновенным распространением гравитации, еще небольшую величину, примерно соответствующую аномальному остатку от обработанных данных наблюдений, тоже преждевременно.
3- Учет скорости распространения гравитации при определение сил гравитационного притяжения между планетами по закону Ньютона показывает, что во-первых процессы протекающие в системе движущейся равномерно и прямолинейно очень отличаются от процессов протекающих в покоящейся системе и такая система не может считаться инерциальной, а во-вторых в такой системе при определенных значениях скорости движения этой системы и скорости распространения гравитации можно получить смещения параметров орбит планет, и в том числе перигелия, полностью соответствующие наблюдаемым значениям и таким образом не только полностью отпадает необходимость в общей теории относительности и любой другой, позволяющих получить аномальный остаток, но и экспериментально доказывается их ошибочность, т.к. из них вытекает аномальное смещение перигелиев, которого в природе нет.
С наилучшими пожеланиями Сергей Юдин. - Re[7]: Смещение перигелия Меркурия и других планет (В. А. Дяденко, 7.12.2007 20:29, 866 Байт, ответов: 25) Уважаемые Юдин и Архангельский! Как я понял,Вы не разобрались с магнитным и электромагнтным устройством атмосфер планет,которое я на своих чертежах и описаниях к ним по течениям вод мировых океанов определил магнитные и электромагнитные свойства мезосферы и ионосферы. Так вот.Все параметры нахождения планет во времени определяются напряжениями ионопотоков между атмосферами планет и солнцем.Смещение нашей планеты от координатных осей из-за уменьшения или из-за повышения напряжения в электромагнтных дугах между ионосферой планеты и Солнцем и Луной,ведет вас в заблуждене.Вы не можете определтся...Расстояния наблюдаемых объектов меняются как в солнечной системе,так и за её пределами...Будьте добры,познакомьтесь с моии работами,хоть и дилетантскими на страничке: http://planeta.times.lv Её нужно скачать.Если не удасться,то её вышлю на ваш Е-майл.
- Re[8]: Смещение перигелия Меркурия и других планет
(С. Ю. Юдин,
10.12.2007 15:32, 1.2 КБайт, ответов: 24)
< tbody>
Цитата: Все параметры нахождения пла нет во времени определяются напряжениями ионопотоков между атмосферами планет и с олнцем. За стремление мне помочь, конечно же спасибо, но навряд ли Ваши исследования будут мне пол езны, т.к. у наиболее интересующе й меня планеты (Меркурия) атмосферы вообще нет.
Астронет | Научная сеть | ГАИШ МГУ | Поиск по МГУ | О проекте | Ав торам Комментарии, вопросы? Пишите: info@astronet.ru или сюда
С наилучшими пожеланиями Серг ей Юдин. - Re[9]: Смещение перигелия Меркурия и других планет
(С. Ю. Юдин,
18.12.2007 18:07, 473 Байт, ответов: 23)
Столкнулся с небольшой проблемой. Нашел кучу данных, например, по скорости Солнца относительно реликтового излучения, но никак не могу найти скорость центра нашей галактики относительно этого излучения. Только в диссертации Д.Макарова нашел упоминание, что эта скорость равна 600 км/с и направлена в сторону Greet Attractor, но каковы координаты этого аттрактора я найти тоже не могу. Если кто в курсе, подскажите.
С наилучшими пожеланиями Сергей Юдин.
- Re[10]: Смещение перигелия Меркурия и других планет
(Дмитрий Доценко,
19.12.2007 11:36, 617 Байт, ответов: 22)
По наблюдениям COBE эта скорость равна 552 +/- 6 км/с. Статья с результатами наблюдений свободно доступна здесь:
http://adsabs.harvard.edu/cgi-bin/nph-bib_query?bibcode=1993ApJ...419....1K
Посмотрите их таблицу 3. Там LSR - local standard of rest (местная инерциальная система отсчета), GC - Galactic Center (центр Галактики), LG - Local Group (Местная Группа). Там же даны галактические координаты всех направлений движения и ссылки, если данные получены не COBE.
Я не знаю, почему они называют галактические координаты l^II и b^II, а не l и b. Может, есть две разные системы гал. координат? - Re[11]: Смещение перигелия Меркурия и других планет
(С. Ю. Юдин,
19.12.2007 17:52, 878 Байт, ответов: 21)
< tbody>
Цитата:
Я не знаю, почему они называют галактические координа ты l^II и b^II, а не l и b. Может, есть две разные системы гал. координат?Спасибо. Суммарная скорость С олнца у меня получилась близкой к ответу, т.е. к значению V=370 км/с, эклиптическая долг ота 171 град, эклиптическая широта -11 град, но у меня вскочил новый вопрос. Почему в литературных источниках мне постоянно встречается утверждение, что Солнце движется прак тически перпендикулярно плоскости эклиптики. А старую систему галактических координат отменили кажется еще в 60-х годах.
С наилучшими пожеланиями Сергей Юдин.
- Re[12]: Смещение перигелия Меркурия и других планет
(Дмитрий Доценко,
20.12.2007 15:56, 344 Байт, ответов: 20)
Литературные источники отличаются в определении инерциальной системы отсчета.
Например, в "Физике космоса" (http://astronet.ru/db/msg/1186374) апекс определен по отношению к LSR (системе отсчета, связанной с ближайшими звездами). Тогда скорость движения Солнца около 20 км/с, а эклиптическая широта апекса больше 50 градусов. - Re[13]: Смещение перигелия Меркурия и других планет
(С. Ю. Юдин,
21.12.2007 20:47, 551 Байт, ответов: 19)
< tbody>
< p>Цитата: Тогда скорость движения Солнца около 20 км/с, а эклиптическая ш ирота апекса больше 50 градусов. По этой скорости я не находил не одной ссыл ки, где бы данные отличались максимум на пару процентов. А вот по скоростям галактики и местной группы галактик очень разнятся в разных литературных источниках, но нигде не указ ывается, что ско
- Re[14]: Смещение перигелия Меркурия и других планет
(С. Ю. Юдин,
16.01.2008 15:05, 1.3 КБайт, ответов: 18)
Скачал файлы с данными JPL (конкретно DE200 и DE405), но никак не могу разобраться как их использовать для вычисления координат планет и Солнца в своей программе, т.к. использовать уже готовые программы я не могу, хотя и скачал одну на С+. То что все данные записаны блоками с данными на 32 дня и каждая запись составляет 826 или 1652 числа по 8 байт я понял. Первые два числа это начало и конец периода в 32 дня в Юлианском исчисление, а далее должны идти коэффициенты для полиномов Чебышева, но не ясно только для координат или и для скоростей планет тоже, т.к. в разных местах написано по разному. Ясно и то, что для разных планет эти коэффициенты расположены в строго определенном месте. Меркурий с 3-ей позиции по 146, Венера с 147 по 182 и т.д. Для DE200 у меня есть расшифровка не только этих позиций, но и дано число коэффициентов аппроксимации, частный интервал аппроксимации в днях (для Меркурия он равен 8 дней) и количество аппроксимируемых данных (для всех планет указано 3, т.е. получается, что коэффициенты даны только для координат), а как это будет для DE405 найти не могу. А если даже и найду, то не знаю что за коэффициенты я считаю и куда их потом подставлять. Если кто-то в курсе, помогите.
С наилучшими пожеланиями Сергей Юдин. - Re[15]: Смещение перигелия Меркурия и других планет
(В. В. Чазов,
16.01.2008 21:31, 840 Байт, ответов: 17)
Дорогие друзья. Уважаемый Сергей, простите великодушно, ежели надоел Вам.
В эфемеридных данных Лаборатории реактивного движения содержатся коэффициенты полиномов Чебышева для вычисления расстояний в километрах.
Дифференцирование каждого полинома по времени позволяет вычислить скорости, повторное дифференцирование даёт значения ускорений небесных тел.
Координаты всех планет и Солнца (кроме пары Земля-Луна) получаются относительно барицентра Солнечной системы. Для пары Земля-Луна даны коэффициенты полиномов для центра масс Земля-Луна. Отдельно, под номером 11, приводятся коэффициенты для определения положения Луны относительно Земли.
Уважаемый Сергей, могу переслать по почте подробные тексты и алгоритмы. Мой адрес прост: vadimchazov@yandex.ru .
С поклоном, Ваш Вадим. - Re[16]: Смещение перигелия Меркурия и других планет
(С. Ю. Юдин,
16.01.2008 23:43, 1.1 КБайт, ответов: 16)
< tbody>
Цитата: Уважаемый Сергей, простите великодушно, ежели надоел Вам.
< /td>< /tbody>А вот и не угодали (ничуть не надоели), т.к. я уже два дня думаю о Вас , а Вы тут как тут - легки на помине (долго жить будете). Кон ечно же высылайте быстрее и тексты и алгоритмы, а то я второй день бороздю просторы И нтернета и не могу найти ничего путнего. Кстати какой файл данных посоветуете DE200 или DE405. Мне нужны данные только по координатам планет и Солнца (скорости не нужны) и желательно только надежные данные и именно наблюдений (пусть немного подправлен ные JPL, но именно наблюдений, а не прогноз на будущее). Я так думаю надежными можно считать данные где-то с 1850 года (а может рань ше?).
P.S. Сообщение для верности дублирую письмом (мой адрес ser@t-k.ru)
С наилучшими пожеланиями Сергей Юди н.
- Re[17]: Смещение перигелия Меркурия и других планет
(В. В. Чазов,
17.01.2008 11:16, 1.6 КБайт, ответов: 14)
Дорогие друзья.
Шаг за шагом решим задачу:
Даны
численные эфемериды Лаборатории реактивного движения США.
Вычислить
вектор положения и вектор скорости планеты Меркурий относительно Солнца 2 марта 2008 года в 21 час московского декретного зимнего времени.
Решение
Полиномы Чебышева T_n(x).
Определены для значений x в интервале -1<=x<=+1.
T_0(x)=1, начальное значение,
T_1(x)=x, начальное значение,
а это уже рекуррентная формула для любого целого положительного значения n:
T_{n+2}(x)=2*x*T_{n+1}(x)-T_{n}(x).
Производные от полиномов Чебышева по переменной x определены в том же интервале -1<=x<=+1.
T'_0(x)=0, начальное значение,
T'_1(x)=1, начальное значение,
а это уже рекуррентная формула для любого целого положительного значения n:
T'_{n+2}(x)=2*x*T'_{n+1}(x)+2*T_{n+1}(x)-T'_{n}(x).
Если известен момент времени t_c лежащий в интервале t_a<=t_c<=t_b, то переход к переменной x и интервалу -1<=x<=+1 выполняется по формуле:
x(t_c)=[t_c-0.5*(t_b+t_a)]/[0.5*(t_b-t_a)].
В эфемеридах для каждой из координат даны численные значения коэффициентов
a_0, a_1, a_2, ... , a_m,
значение положения по координате определено формулой:
r_x(t_c)=a_0*T_0(x(t_c))+a_1*T_1(x(t_c)) +a_2*T_2(x(t_c))+...a_m*T_m(x(t_c)),
значение скорости по координате определено формулой:
v_x(t_c)=[a_0*T'_0(x(t_c))+a_1*T'_1(x(t_c)) +a_2*T'_2(x(t_c))+...a_m*T'_m(x(t_c))]*[(2*t_c)/(t_b-t_a)].
Единица измерения положений - километры.
Единица измерения скоростей - километры за сутки.
До встречи, Ваш Вадим. - Re[18]: Смещение перигелия Меркурия и других планет
(С. Ю. Юдин,
17.01.2008 14:19, 2.2 КБайт, ответов: 13)
Вадим, большое спасибо. Сильно меня выручили с полиномами Чебышева, но перейти к вычислениям я пока не могу, т.к. остались не выясненными некоторые моменты. Например, Вы для вычисления и координат и скоростей записали в формулах одни и те же коэффициенты a_0, a_1, a_2 a_m, а в файле DE405 содержится в два раза больше записей (чисел) в каждом блоке данных, чем в DE200, т.е. 1652 против 826. И, если количество аппроксимируемых переменных и число коэффициентов аппроксимации осталось то же самое, то не понятно, что аппроксимируют лишние 826 записей в файле DE405. Я думал, что это коэффициенты для скоростей, а у Вас выходит, что скорости можно определить по тем же самым коэффициентам, что и координаты. Какова вообще структура данных в DE405. Как я понял в DE200, например, для Меркурия с третьей позиции идут коэффициенты a_0_X, a_0_Y, a_0_Z a_m_X, a_m_Y, a_m_Z, а количество коэффициентов и другие параметры определяются по схеме, которую я прочитал в статье, расположенной на Вашем сайте, а конкретно // Весь массив из 826 чисел расшифровывается с помощью пяти массивов целых чисел:
N object i j k l m
1 Mercury 3 146 12 8 3
2 Venus 147 182 12 32 3
3 Earth-Moon 183 272 15 16 3
4 Mars 273 302 10 32 3
5 Jupiter 303 329 9 32 3
6 Saturn 330 353 8 32 3
7 Uranus 354 377 8 32 3
8 Neptune 378 395 6 32 3
9 Pluto 396 413 6 32 3
10 Moon 414 701 12 4 3
11 Sun 702 746 15 32 3
12 Nutation 747 826 10 8 2
где i - начальный номер в массиве, j - конечный номер в массиве, k - число коэффициентов аппроксимации, l интервал частной аппроксимации в днях внутри общего интервала, m - количество аппроксимируемых переменных.// Желательно бы взглянуть на подобную схему и для файла DE405. И потом, в связи с тем, что для Меркурия внутри общего интервала времени для данных существуют еще и частные интервалы, то получается, что x(t_c)=[t_c-0.5*(t_b+t_a)]/[0.5*(t_b-t_a)] надо рассчитывать по значениям t_a и t_b, которые будут равны времени на концах частного интервала. Или я не прав и их надо брать в начале и конце общего интервала, а коэффициенты использовать из частного интервала.С наилучшими пожеланиями Сергей Юдин.
- Re[19]: Смещение перигелия Меркурия и других планет
(В. В. Чазов,
17.01.2008 14:35, 308 Байт)
Простая работа над ошибками:
Следует читать
значение скорости по координате определено формулой: v_x(t_c)=[a_0*T'_0(x(t_c))+a_1*T'_1(x(t_c)) +a_2*T'_2(x(t_c))+...a_m*T'_m(x(t_c))]*[2/(t_b- t_a)].
2/(t_b-t_a) - это масштабный множитель. Простите, трудно с формулами на Форуме. Вадим. - Re[19]: Смещение перигелия Меркурия и других планет
(В. В. Чазов,
17.01.2008 15:03, 2.2 КБайт, ответов: 4)
Дорогие друзья, на нашем Форуме возникают прекрасные вопросы, на которые не могу ответить
однозначно. Например
Кстати, какой файл данных посоветуете DE200 или DE405?
Международный астрономический союз рекомендует использовать модель DE405/LE405. При создании этой модели были учтены результаты космических миссий и наземные наблюдения планет после 1973 года (до 1997 года). В DE405/LE405 немного исправлена система отсчёта, то есть основная плоскость, в которой вычисляются положения планет, совпадает с плоскостью стандартного экватора, задаваемого положениями далёких квазаров. Но кто из нас эти квазары видел?
Использую в практических целях DE200 и не встречаю неприятностей.
Ещё один замечательный вопрос о наблюдениях, использованных при построении моделей.
В моделях серии DE использованы наблюдения планет-гигантов на меридианном круге обсерватории Вашингтон, выполненные с 1904 года. Учтено несколько серий наблюдений внутренних планет на различных меридианных кругах и астролябиях, полученных также в 20 веке.
Но основной вес получили радиолокационные измерения расстояний как до самих планет, так и до аппаратов космических миссий. В случае Луны основными являются результаты лазерной локации, проводимые с 1971 года.
Наблюдения прохождений Меркурия и Венеры по диску Солнца, планомерно начатые во Франции учёными-энциклопедистами 18 века, использованы только для улучшения равномерности шкалы времени.
Наблюдения, с которыми работали мэтр Урбан Леверрье и сэр Саймон Ньюком, вообще не приняты во внимание.
Друзья, этот факт, вероятно, более всего огорчит Вас. При словах о смещении перигелия ссылаются на достижения 19 века, но о наблюдениях тех лет - ни гу- гу.
Впрочем, и мэтр Урбан Леверрье и сэр Саймон Ньюком принимали к вычислениям только собственные наблюдения.
Учёные всех времён и народов - весьма оригинальны, всегда служат по контракту, обязаны отчитаться, кто перед интендантом финансов, кто перед конгрессом, кто перед фондом. В связи с этим каждому приходится выставлять вперёд собственные достижения - наблюдения, теории, модели. О предшественниках лучше не напоминать, всё равно грантов с ними не разделишь.
Вадим. - Re[20]: Смещение перигелия Меркурия и других планет
(С. Ю. Юдин,
18.01.2008 9:50, 3.2 КБайт, ответов: 3)
< tbody>
Цитата:
Наблюдения прохождений Меркурия и Венеры по диску Солн ца, планомерно начатые во Ф ранции учёными-энциклопеди стами 18 века, использованы только для улучшения равномерности шкал ы времени.
Наблюдения, с которыми работали мэтр Урбан Леверрье и сэр Саймон Ньюком, вообще не приняты во внимание.
Друзья, этот факт, вероятно, более всего огорчи т Вас. При словах о смещении перигелия ссылаются на достижения 19 века, но о наблюдениях те х лет - ни гу- гу.Я не только огорчился, но и нич его не понял. А разве статью ЧИСЛЕННЫЕ И АНАЛИТИЧЕСКИЕ ТЕОРИИ ДВИЖЕНИЯ БОЛЬШИХ ПЛАНЕТ СОЛНЕЧН ОЙ СИСТЕМЫ, которую я скачал с Вашего сайта http://vadimchazov.narod.ru/text_pdf/particl1.pdf не Вы пи сали. А то там написано, что эфемериды очень даже совпадают с аналитическими эфемеридами Ньюкома на интервале времени от 1850 до 1895 годов. На всякий случай приведу цитату из стать и.
//Эфемерида DE200/LE200 включает в себя все новейшие научные разработки. Числен ное интегри рование уравнений движения выполнено в инерциальной системе отсчета с началом в барицентре Со лнечной системы. В качестве аргумента интегрирования использовано равномерное барицен трическое динамическое время прямой потомок эфе меридного времени. Учтены релятивистские эффекты. Система гравитирующих тел дополнена пять ю массивными астероидами. За основную плоскость выбрана плоскость экватора, фиксированного на эпоху J200 0.0. Использованы радиолокационные наблюдения планет земной группы, лазерные наблюдения Луны и данные о параметрах движения космических аппаратов при сближении их с большими плане тами. Результаты аналитической теории движения четырех внутренних планет, созданной Нь юкомом, п риняты во внимание самым непосредственным образом: новые численные эфемериды составл ены так, что наилучшим образо м совпадают с аналитическими эфемеридами Ньюкома на интервале времени от 1850 до 1895 год ов.//
С наилучшими пожеланиями Сергей Юдин.
Астро нет | Научная сеть | ГАИШ МГУ | Поиск по МГУ | О проекте | Авторам Коммента рии, вопросы? Пишите: info@astronet.ru или сюда ⬹䘥┲㕅䔥╅う䔥┸㡅┫㑅䔥┲㡅䔥 㕅䔥╄㡅䘥⭆䘥┷㕅䘥┲䉆䘥┰㕅䘥⬵ ┲䑅䘥┳㉆䘥┰㕅䔥 䑅䔥┸㕆䄥⬰䔥 - Re[21]: Смещение перигелия Меркурия и других планет
(В. В. Чазов,
18.01.2008 15:34, 857 Байт, ответов: 2)
Дорогие друзья, всё правильно.
Наблюдения 19 века не использовались, а начальные условия на интервале времени 1850-1895 годы подобрали так, чтобы результаты численного интегрирования на этом интервале представляли в среднем координаты внутренних планет, вычисленные по таблицам сэра Саймона Ньюкома.
Более того, но, пожалуйста, не делайте никаких оргвыводов, современные учёные Парижа, гордящиеся своей собственной теорией движения планет, вообще не принимали во внимание никакие наблюдения. Они раньше всех получали по договорённости результаты Лаборатории реактивного движения США и аппроксимировали их рядами Фурье.
Это очень научные методы. Важно отчитаться так, чтобы парламенты и национальные собрания поверили и выделили ассигнования на "новые разработки".
С поклоном, Вадим. - Re[22]: Смещение перигелия Меркурия и других планет
(В. В. Чазов,
18.01.2008 15:48, 1.0 КБайт)
Dear Friends, это простое дополнение к ответу под номером 20.
Представьте себе, сработала привычка простого советского инженера: поставил задачу, долго и нудно рассказывал, как её следует решать, а результатов не привёл.
А результаты то есть, вот они:
гелиоцентрические эклиптические координаты, долгота и широта в градусах, минутах, секундах и расстояние в астрономических единицах
2008 03 02 18 00 00.000 date in UTC
162 33 29.5 -00 00 35.5 00.99003 Луна
162 25 30.3 +00 00 00.8 00.99132 Земля
232 17 46.1 -00 29 19.7 00.45553 00.190 Меркурий
124 41 02.5 +01 47 17.2 01.64113 00.198 Марс
281 53 08.7 -01 26 57.3 00.72756 -3.749 Венера
276 40 32.7 +00 05 10.1 05.22526 -2.028 Юпитер
155 18 01.1 +01 39 17.2 09.28244 00.456 Сатурн
348 28 03.0 -00 46 11.3 20.09633 05.945 Уран
321 43 53.3 -00 18 23.9 30.04105 07.973 Нептун
269 03 18.8 +06 22 30.1 31.42581 13.993 Плутон
Yours ever, Vadim. - Re[22]: Смещение перигелия Меркурия и других планет
(С. Ю. Юдин,
18.01.2008 22:12, 1.1 КБайт)
< tbody>
Цитата: Дорогие друзья, всё правильно.< br />Наблюдения 19 века не использовались, а начальные условия на интервале времени 1850-1895 го ды подобрали так, чтобы результаты численного интегрировани я на этом интервале представляли в среднем координаты внутренних планет, вычисленные по таблицам сэра Саймона Ньюкома.
Вадим, а нельзя ли попроще. Я ведь н е астроном, а Вы отлично знаете зачем мне все это надо. Так вот ответьте попроще. Могу ли я использовать данные JPL, как данные пассивного натурного эксперимента (наблюдат ельные данные) для определения по результатам активного многофакторного вычислительного экс перимента скорости Сол нца и скорости распространения гравитации или данные JPL это те же самые данные, что дает и моя программа, но только немного поточнее, по тому, что инте грирование проводилось на отн осительно малень
- Re[19]: Смещение перигелия Меркурия и других планет
(В. В. Чазов,
17.01.2008 15:26, 1.4 КБайт, ответов: 6)
Dear Friends.
Один массив, работающий на интервале времени 32 дня, в модели DE405/LE405 содержит 1018 чисел. Расшифровать данные можно с помощью таблицы: N object i j k l m
1 Mercury 3 170 14 8 3
2 Venus 171 230 10 16 3
3 Earth-Moon 231 308 13 16 3
4 Mars 309 341 11 32 3
5 Jupiter 342 365 8 32 3
6 Saturn 366 386 7 32 3
7 Uranus 387 404 6 32 3
8 Neptune 405 422 6 32 3
9 Pluto 423 440 6 32 3
10 Moon 441 752 13 4 3
11 Sun 753 718 11 16 3
12 Nutation 819 898 10 8 2
13 Libration 899 1018 10 8 3
Число l - количество суток короткого интервала аппроксимации внутри всего интервала длиной 32 дня.
Для Меркурия, например, интервал 32 дня разделён на четыре подинтервала по 8 дней каждый.
Для Луны, например, интервал 32 дня разделён на восемь подинтервалов по 4 дня каждый.
Для Солнца, например, интервал 32 дня разделён на два подинтервала по 16 дней каждый.
Число m- количество переменных для аппроксимации. Для всех объектов это число равно 3 - ибо в декартовом мире три координаты. Для нутации аппроксимированы изменения двух величин, нутации в долготе и нутации в наклоне. Пункт 13 - это аппроксимация числовых значений трёх углов Эйлера вращения Луны, данные необходимы при обработке лазерных наблюдений уголковых отражателей на нашем спутнике.
До встречи. Ваш Вадим. - Re[20]: Смещение перигелия Меркурия и других планет
(В. В. Чазов,
17.01.2008 16:04, 2.2 КБайт, ответов: 5)
Дорогие друзья, продолжим.
На момент T_{eph}=2454528.25075444 надо вычислить положение Меркурия относительно Солнца.
Среди текстовых файлов эфемериды DE200/LE200 находим файл ascp2000.200. В этом файле есть массив из 826 чисел, необходимых для нашего момента времени.
Действительно, этот массив расположен под номером 94, начинается с юлианской даты 2454512.5, работает до юлианской даты 2454544.5.
Для Меркурия разбиваем интервал на четыре части, по 8 дней:
1. 2454512.5 - 2454520.5,
2. 2454520.5 - 2454528.5,
3. 2454528.5 - 2454536.5,
4. 2454536.5 - 2454544.5,
Наш момент t_c=2454528.25075444 попадает во второй интервал, в таком случае
(t_a=2454520.5) < t_c < t_b=2454528.5.
Вычисляем номер ячейки в массиве из 826 чисел, с которой начинаются коэффициенты аппроксимации для второго интервала.
Начальный номер i=3.
Число коэффициентов для каждой переменной k=12.
Число переменных m=3.
Общее число ячеек для одного подинтервала равно (k*m)=36. Второй интервал начинается с элемента массива номер 3+36=39.
Первые двенадцать чисел - коэффициенты
a_0, a_1, a_2, ... , a_11 для координаты x.
Элементы с номера 51 по номер 62 - для координаты y.
Элементы с номера 63 по номер 74 - для координаты z.
Преобразуем момент времени t_c к интервалу изменения [-1,+1]:
x(t_c)=[t_c-0.5*(t_b+t_a)]/[0.5*(t_b-t_a)],
по рекуррентному алгоритму вычисляем числовые значения полиномов Чебышева от T_0(x(t_c)) до T_{11}(xt(_c)),
с помощью коэффициентов аппроксимации вычисляем по отдельности три координаты Меркурия на заданный момент.
Но мы получим положение Меркурия относительно барицентра Солнечной системы относительно неподвижного экватора.
Для вычисления положения Меркурия относительно Солнца надо вычислить координаты Солнца относительно барицентра. Вычисления выполняются по тому же алгоритму, только номера ячеек в массиве другие.
Из каждой координаты Меркурия надо вычесть соответствующую координату Солнца.
Для перехода из плоскости экватора в плоскость эклиптики следут выполнить поворот против часовой стрелки на угол \varepsilon - угол наклона эклиптики к экватору.
С поклоном, Ваш Вадим. - Re[21]: Смещение перигелия Меркурия и других планет
(С. Ю. Юдин,
20.01.2008 11:06, 2.9 КБайт, ответов: 4)
< tbody>
Цитата: Для перехода из плоскости э кватора в плоскость эклиптики следут вы полнить поворот против часовой стрелки на угол \varepsilon - уго л наклона эклиптики к экватору.
С поклоно м, Ваш Вадим.Вадим, большое спасибо з а очень подробные рекомендации (кстати и в ал горитме, который Вы мне прислали очень много комментари ев, а то мне на Мембране тоже прислали ал горитм и тоже на Turbo Pasсal 7, но абсолют но без комментариев ничего понять нельзя), но у меня есть еще о дин вопрос. Допустим, угол накло на эклиптики к экватору в стан дартную эпоху J2000.0 мне извест ен 23 гр 26 мин 21,448 сек, но к ак конкретно перевести экваториальные коор динаты в эклиптические я сомневаюсь. Нап ример, надо ли учитывать нутацию в стандартн ую эпоху J2000.0 равную 9,2025 сек и зачем в фай лах JPL даны данные по нутации на конкретную дату . Напишите пожалуйста конкре тные формулы как перевести экваториальные координаты в эклиптические, а то, даж е если я и разберусь по уче бникам в этих тонкостях, я все равно буду сомневаться в сво их формулах.
P.S. Свой вариант алгоритма расчета координат п о данным JPL, т.е. адаптированный для програ ммы Solsys я написал, но координаты пока получают ся хоть и похожими, но не те, что надо. Буду искать ошибку .
С наилучшими пожеланиями Сергей Юдин.
Астронет | Научная сеть | ГАИШ МГУ | Поиск по МГУ | О проекте | Авторам Комментарии, вопросы? Пишите: info@astronet.ru или сюда }(xt(_c)),
с помощью коэффициентов аппроксимации вычисляем по отдельности т и координаты Меркурия на заданный момент.
Н мы получим положение Меркурия относительно барицентра С лнечной системы относительно неподвижного экватора.
Д я вычисления положения Меркурия относительно Солнца н до вычислить координаты Солнца относительно барицентра. В числения выполняются по тому же алгоритму, только номера ячеек в массиве другие.
И каждой координаты Меркурия надо вычесть соответствующую к ординату Солнца.
Д я перехода из плоскости экватора в плоскость эклиптики с едут выполнить поворот против часовой стрелки на угол \varepsilon - у ол наклона эклиптики к экватору.
С поклоном, Ваш Вадим. < table> & bsp; - Re[22]: Смещение перигелия Меркурия и других планет
(В. В. Чазов,
20.01.2008 16:03, 981 Байт, ответов: 3)
Добрый день, Сергей.
Значение угла наклона эклиптики к экватору в стандартную эпоху \varepsilon следует перевести в радианы
\varepsilon = (3.141592653589793/180)*(23+(26+21.448/60)/60)
и вычислить синус \sin\varepsilon
косинус \cos\varepsilon этой величины.
Эфемерида Лаборатории реактивного движения США позволяет вычислить прямоугольные координаты
x, y, z,
в системе стандарного экватора на любую дату.
Прямоугольные координаты
X, Y, Z
относительно плоскости фиксированной эклиптики вычисляются по формулам:
X = x;
Y = +y*\cos\varepsilon + z*\sin\varepsilon;
Z = -y*\sin\varepsilon + z*\cos\varepsilon;
то есть с помощью поворота против часовой стрелки вокруг оси OX на угол \varepsilon.
Плоскость эклиптики сохраняет неизменное положение относительно удалённых (неподвижных) радиоисточников.
Поклон всем друзьям, до встречи, Ваш Вадим. - Re[23]: Смещение перигелия Меркурия и других планет
(В. В. Чазов,
20.01.2008 16:28, 1.5 КБайт, ответов: 2)
Дорогие друзья, простите, что без приветствия,
просто хочу продолжить.
При таких преобразованиях прецессию и нутацию учитывать не надо, ибо все действия происходят в системе стандартных экватора и эклиптики.
Мгновенные значения нутации в долготе и нутации в наклоне приводятся в численных эфемеридах JPL для удобства тех пользователей, которые обрабатывают наблюдения, выполняемые с вращающейся Земли.
Значения двух этих величин программа численного интегрирования JPL не улучшает по результатам наблюдений, а использует готовые формулы для их вычисления.
Друзья, боюсь Вас запутать, но мгновенные значения этих параметров в процессе численного интегрирования, выполненного в Лаборатории реактивного движения, были использованы в следующем контексте:
для учёта динамического взаимодействия фигуры вращающейся Земли и двух материальных точек, Солнца и Луны.
Авторы и создатели столь замечательных эфемерид не советуют использовать значения нутации в долготе и нутации в наклоне, приводимые в данных DE200/LE200. Объяснение простое - числовые значения параметров вычислены по разложениям Вуларда 1954 года. В 1980 году астрономы перешли на новую модель прецессии и нутации, а на рубеже веков повторили подвиг своих учителей и рекомендовали к использованию ещё более новую модель.
Впрочем, как говорят посетители Измайловских прудов, подробности за домино.
С поклоном, Ваш Вадим. - Re[24]: Смещение перигелия Меркурия и других планет
(С. Ю. Юдин,
22.01.2008 14:29, 582 Байт, ответов: 1)
Прогнал на своей программе два пробных файла с данными JPL, т.е. с данными за 20 лет, но мне нужны полностью файлы DE200 и DE405, а на FTP сервере JPL ftp://ssd.jpl.nasa.gov/pub/eph/export/ я их не нашел (там только куски по 20 лет). Где можно скачать эти файлы еще. И потом, мне наверное более желательно иметь файлы последовательного доступа, т.е. ascii, т.к. просмотреть их может любой даже Блокнотом, а читать их мне все равно надо последовательно от начала и до конца.
С наилучшими пожеланиями Сергей Юдин.
- Re[25]: Смещение перигелия Меркурия и других планет
(В. В. Чазов,
22.01.2008 21:14, 451 Байт)
Дорогие друзья, только несколько слов. На страничке ftp://ssd.jpl.nasa.gov/... содержатся
именно ASCII файлы по 20 лет каждый. (Объём каждого файла в текстовом формате для
DE200/LE200 - 5201506 bytes, для DE405/LE405 - 6403298 bytes).
Можно читать каждый файл по очереди, можно собрать их в один большой файл, это уже по
желанию.
Там есть ещё наборы данных в двоичном формате, но это для пользователей системы UNIX.
С поклоном, Вадим. - Re[17]: Смещение перигелия Меркурия и других планет
(В. В. Чазов,
17.01.2008 11:46, 1.4 КБайт)
Дорогие друзья, продолжим.
Шаг за шагом решаем задачу:
Даны
численные эфемериды Лаборатории реактивного движения США.
Вычислить
вектор положения и вектор скорости планеты Меркурий относительно Солнца 2 марта 2008 года в 21 час московского декретного зимнего времени.
Решение
Переведём московское время во Всемирное координированное время
UTC=02.03.2008 18 hour 00 minute 00 second (минус 3 часа зимой).
. Переведём момент времени из шкалы UTC в шкалу земного времени TT
TT=UTC+65.184 second=02.03.2008 18 hour 00 minute 65.184 second.
Вычислим юлианскую дату, соответствующую нашему моменту времени:
TT(jd)=2454528.25075444 (сутки и доли суток в шкале земного времени).
С помощью небольшой поправки (менее 0.002 секунды времени) перейдём из шкалы земного времени TT в шкалу равномерного времени T_{eph} численной эфемериды Лаборатории реактивного движения США:
d=(2454528.25075444-2451545.0)/36525;
g=(3.141592654/180)*(357.528+35999.050*d); (в радианах)
T_{eph}=TT(jd)+(0.001658*Sin(g+0.0167*Sin(g)))/86400.e0;
В марте угловая величина g равна приблизительно 0 градусов, то есть и поправка на равномерную шкалу - нулевая.<\br> Именно на момент T_{eph}=2454528.25075444,
соответствующий нашей исходной дате, следует вычислять положения и скорости по данным эфемериды.
До встречи, Ваш Вадим. - Re: Смещение перигелия Меркурия и других планет
(С. Ю. Юдин,
18.01.2008 22:14, 285 Байт, ответов: 1)
ких интервалах времени, когда начальные условия для интегрирования постоянно подправлялись (не известно как), т.е. данные JPL это не аппроксимация экспериментальных наблюдательных данных, а гибридные данные с неизвестным названием.
С наилучшими пожеланиями Сергей Юдин.
- Re[2]: Смещение перигелия Меркурия и других планет
(В. В. Чазов,
19.01.2008 7:58, 745 Байт)
Дорогие друзья, уважаемый Сергей.
С каждым часом убеждаюсь в своей двойственности. Вопросы становятся сложнее, а отвечать всё труднее.
Данные JPL - это аппроксимация экспериментальных наблюдательных данных.
Сергей, в Вашей терминологии - это данные пассивного натурного эксперимента (наблюдательные данные). Конечно же, такие замечательные и легкодоступные материалы можно использовать и для Вашей задачи.
Использую численные эфемериды Лаборатории реактивного движения США для обработки и планирования наблюдений, для прогноза движения малых тел Солнечной системы. В СССР первые магнитные ленты с эфемеридами появились в год Олимпиады. Это событие было очень заметным.
С поклоном, Вадим. - Re: Смещение перигелия Меркурия и других планет
(С. Ю. Юдин,
20.01.2008 15:42, 444 Байт)
Вообще то сами формулы у меня есть, но я не уверен, что это окончательное преобразование. Так, если угол наклона эклиптики к экватору в стандартную эпоху J2000.0 Betta= 23 гр 26 мин 21,448 сек, то координаты в плоскости эклиптики должны быть
Xecl=X
Yecl= Y * cos(Betta) + Z* sin(Betta)
Zecl= Z * cos(Betta) - Y* sin(Betta)
Я все правильно записал? Ничего уточнять больше не надо?С наилучшими пожеланиями Сергей Юдин.
- Re: Смещение перигелия Меркурия и других планет
(С. Ю. Юдин,
8.02.2008 12:12, 10.0 КБайт)
Наконец не только разобрался с эфемеридами JPL, но и нашел Российские эфемериды на сайте Лаборатория эфемеридной астрономии (заведующий лабораторией Питьева Елена Владимировна) http://www.ipa.nw.ru/PAGE/DEPFUND/LEA/RUS/ruslea.htm . У них там написано, что в их лаборатории в 2005 году
//Совместным интегрированием планет, Луны, Солнца, 301 крупного астероида с учетом возмущений от сжатия Солнца и кольца малых астероидов построены высокоточные численные эфемериды планет EPM2004 на интервале 1880 - 2050 гг. Доступны по FTP эфемериды EPM2004. Построенные эфемериды EPM положены в основу национального "Астрономического ежегодника" с 2006 г.//
Вот только скачать их с указанного там FTP сервера, чтобы убедиться в их реальности я не смог (оказывается, нет у меня какого-то доступа туда), по этому вызывает подозрение и утверждение о том, что для "Астрономического ежегодника" с 2006 г. будут использоваться эти эфемериды. Тем более, что я нашел в Интернете сообщение о том, что
//Структура Морского астрономического альманаха на 2005-2006гг. по сравнению с предыдущим выпуском МАА-2 не претерпела существенных изменений. При этом радикальной переработке подверглась теоретическая основа эфемерид. Заменена теория движения тел Солнечной системы с DE200/LE200 на DE405/LE405, в которой координаты и скорости объектов представлены с помощью полиномов Чебышева.
Директор Института прикладной астрономии РАН
член-корреспондент РАН А.М. Финкельштейн//И даже если эфемериды EPM2004 действительно существуют, то еще не известно насколько они отличаются от эфемерид DE405/LE405 (может быть это вообще калька). В общем, я решил пока поработать с эфемеридами DE405/LE405. Вот только у меня возникли некоторые вопросы по статистической обработке данных полученных по этим эфемеридам. К сожалению ни на одном математическом сайте, а я обращался на три, никто так ничего и не посоветовал мне и проблема правильности моей методики статистической обработки данных осталось не решенной (то ли вопрос для математиков оказался не интересным, то ли не было готового ответа на него в учебнике - не знаю). По этому опять обращаюсь за помощью к астрономам и постараюсь изложить еще и на этом сайте суть проблемы, но уже с конкретными примерами на обработанных данных псевдонаблюдений Лаборатории Реактивного Движения (JPL, США).
На первом рисунке Вы видите фрагмент формы работы со статистикой программы Solsys5, где по оси абсцисс отложено в масштабе MT время, а по оси ординат значения аргумента перигелия (в градусах) на конкретную дату, когда планета Земля прошла точку своего перигелия. Эти значения угла в перигелии я получил на второй форме программы Solsys5, т.е. на форме проведения вычислительного эксперимента и использовал для определения угла в перигелии ту же методику, что и при проведение вычислительного эксперимента, но сами координаты планет брал не из математической модели, а из фонда DE405. Начальная дата обработки данных 1601 год, а конечная 2000, т.е. обработаны данные наблюдений за 400 лет, а точность замера угла в перигелии была в интервале менее 1 угловой секунды. И таким образом, можно считать, что параметры орбит, полученных как на математической модели, так и при обработке наблюдательных данных астрономов, не имеют ошибки измерений параметров орбит, т.к. эта ошибка, как минимум на порядок, меньше величины псевдослучайных отклонений параметров орбит, т.е. отклонений под воздействием других планет, и, следовательно, полученные значения параметров орбит являются типичными случайными величинами с нормальным законом распределения и, к которым применимы типичные статистические методы обработки данных.
http://ser.t-k.ru/Ris/Zemlia1.gif
Как видно из рисунка, если мы разобьем всю выборку на группы (для Земли получилось 6 групп по 60 точек) и посчитаем среднее значение параметра в группах (здесь и далее приведены данные только по перигелию планет) и поставим один большой черный кружок с ординатой равной среднему значению угла в середине интервала, то у нас получится примерно прямая линия (синяя). А на расстояние двух стандартов (среднеквадратических отклонения) получившихся при статистической обработке всей выборки (398 точек) проведем две линии (зеленых), которые будут границами доверительных интервалов для угла при доверительной вероятности (надежности) 95%, т.е. эти интервалы с вероятностью 95% накрывают весь массив точек, т.е. это будет предельная ошибка определения параметра по выбранной нами формуле определения параметра. На всякий случай напоминаю, что предельная ошибка без указания надежности не имеет никакого смысла. А из классической теории ошибок измерений известно, что результаты многократных измерений одной и той же величины должны лежать в пределах +/- 3*sigma (sigma - стандартное отклонение, т.е. среднеквадратичное), но для разной надежности (доверительной вероятности) полученных данных требуется разное количество измерений, чтобы значения параметров с этой вероятностью не выходили за какие то границы. И доверительный интервал для доверительной вероятности 95% составляет +/- 2*sigma.
Теперь, что касается различных примененных мною методик статистической обработки, как я их называю, первичных данных, т.е. значений угла в перигелии для конкретного времени полученных или по данным наблюдений или по данным математической модели, по которым у меня и возникли некоторые вопросы. Самым простым является обычная обработка всего массива данных (всей выборки) по углу и получения для угла в перигелии уравнения регрессии в функции от времени вида
Alfa=k0+k1*dT+k2*dT^2 (3a)
Но многие параметры и для многих планет имеют квазистабильное значение смещения, т.е. не изменяемое со временем. Вернее сами смещения параметров орбит планет постоянно меняются из-за объективных причин, т.е. воздействия одних планет на другие, но одни значения вековых смещений параметров орбит просто немного колеблются относительно какого то среднего значения, а у других это среднее значение еще и изменяется со временем. По этому в таком виде (наличие всех трех коэффициентов) эта зависимость будет уместна только для Венеры и Урана и то на очень больших временных интервалах, а для основной массы планет будет достаточно усеченной формулы
Alfa=k0+k1*dT (2a)
А для Нептуна и Плутона достаточно только одного коэффициента, т.к. у них можно записать, что
Alfa=k0 (1a)
Но все же нам будет более интересно получить именно зависимости (2a) или (3a), т.к., взяв потом первую производную от этих выражений, мы получим выражения для вековых смещений параметров орбит (если у нас время в формулах (2a) и (3a) будет измеряться столетиями).
dAlfa=k1 (1dа)
dAlfa=k1+2*k2*dT (2dа)И обычно при статистической обработке данных задача состоит в определении коэффициентов таким образом, чтобы сумма квадратов расстояний по вертикали от экспериментальных точек до графика функции аппроксимирующей эти точки была наименьшей. И построение эмпирической формулы состоит из двух этапов: выяснение общего вида этой формулы и определение ее наилучших параметров. При этом для проверки согласия построенной кривой регрессии с результатами эксперимента обычно вводят следующие числовые характеристики: коэффициент корреляции (линейная зависимость), корреляционное отношение и коэффициент детерминированности (нелинейная зависимость). Но мне то надо не просто проверить на адекватность описания выбранный вид уравнения регрессии по какому то критерию (к тому же может получится, что все три уравнения будут адекватно описывать экспериментальные данные), а получить предельную ошибку измерений в абсолютных единицах для заданной надежности данных и не только для различных аппроксимаций, но и для различных аппроксимаций полученных при различных методиках обработки данных и вот тут у меня возникают вопросы на которые я сам ответить не могу и мне требуется Ваша помощь.
В принципе, после получения уравнений (1dа) или (2dа) можно было бы считать задачу определения вековых смещений решенной и Ньюком и исследователи в Лаборатории реактивного движения на этом и успокоились. Правда в JPL для всех параметров планет ограничились только уравнениями (2a), а Ньюком еще в 1895 году пошел гораздо дальше и почти для всех перигелиев планет получил уравнения с четырьмя коэффициентами и только для Меркурия и Венеры с тремя (3a) и для Плутона с одним коэффициентом (1a) и теперь эти его аппроксимации даже называются теорией планет Ньюкома. Но возникает один каверзный вопрос а какова ошибка определения вековых смещений по формулам (1dа) или (2dа) полученным по такой методике. Ведь для значений вековых смещений параметров по этой методике у меня получается по формулам (1dа) и (2dа), соответственно, 1156 и 1163 угловых секунды, а стандарт (среднеквадратическое отклонение) для самого параметра (угла в перигелии) получился по 283 угловых секунды, т.е. при доверительной вероятности 95% получается доверительный интервал +/- 566 угловых секунд (2*sigma). Очевидно, что этот же доверительный интервал мы должны распространить и на вековые смещения, но тогда от полученных результатов будет мало пользы. А если мы посмотрим на следующий рисунок для Венеры, где для полученных вековых смещений 40 и 33 угловых секунды у нас доверительный интервал будет +/- 1288 секунд, то о том, чтобы полученные результаты где-то использовать не может быть и речи.
http://ser.t-k.ru/Ris/Venera1.gif
По этому я в последних двух версиях программы Solsys и занимался в основном совершенствованием методики определения вековых смещений и кое-что у меня получилось, но вот насколько это законно с научной точки зрения я не знаю. Вычисление стандарта, т.е. sigma (среднеквадратичного отклонения) я производил по следующей формуле
sigma=sqrt(Sum((Y(i)-Y)^2)/(N-Nk)) (4)
где для формул (1a, 2a, 3a) Y=Alfa, N - количество первичных данных по параметру, а Nk количество коэффициентов в этих формулах.
(смотрите продолжение) - Re: Смещение перигелия Меркурия и других планет
(С. Ю. Юдин,
8.02.2008 12:17, 9.0 КБайт, ответов: 1)
ПРОДОЛЖЕНИЕ
Обычно астрономы для полученных ими значений вековых и периодических смещений параметров орбит не указывают ни доверительной вероятности ни доверительного интервала, т.к. получают их используя теорию возмущений с аналитическим решением дифференциальных уравнений в правых частях которых записаны пертурбационные функции, т.е. сумма гармоник от возмущений других планет. А желательно бы, тем более, что для того, чтобы эти дифференциальные уравнения, а также уравнения для определения теоретического смещения по какой то теории, можно было решить, в них к тому же делается множество допущений. А, если мы хотим убедительно доказать, что какая то физическая теория соответствует или не соответствует экспериментальным данным, то мы обязательно должны указывать при высокой надежности экспериментальных данных и доверительные интервалы этих данных. И, например, Ньюком при сравнение наблюдательных данных по вековым смещениям 4-х параметров 4-х внутренних планет с расчетными, полученными с использованием теории Ньютона, кругом указал вероятные ошибки для этих смещений. А затем уже, сравнивая разность между этими значениями, т.е. получившийся остаток с вероятной ошибкой определения этого остатка, он делал вывод является ли этот остаток аномальным, т.е. не укладывающимся в доверительный интервал погрешности его определения и, следовательно, не объясняемый классической теорией тяготения. Например, для Меркурия он получил наблюдаемое значение векового смещения перигелия 575,06 +/- 1,95 расчетное 533,82 +/- 0,78 и остаток 41,24 +/- 2,09 и сделал вывод, что смещение его перигелия не объясняется теорией Ньютона, а для Венеры он получил наблюдаемое значение 42,52 +/- 29,33 расчетное 49,85 +/- 21,99 и остаток минус 7,33 +/- 36,66 и сделал вывод, что достоверность этого остатка не достаточна для того, чтобы говорить о том, что он не объясняется теорией Ньютона.
Таким образом, Ньюком сделал вывод, что из проверенных им 15 смещений только 4-е не объясняются теорией Ньютона (перигелии Меркурия и Марса, узлы Венеры и эксцентриситет Меркурия). Вот только определял он эти вероятные ошибки не стандартными статистическими методами, и быстрее всего речь у него идет о точности замера положений планет при наблюдении за ними и точности определения их масс, а не о точности определения средних значений наблюдательных данных вековых смещений. А вот при определение средних ошибок расчетных значений он исходил только из вероятных средних ошибок определения масс планет. Таким образом, т.к. применяемый астрономами метод возмущений не позволяет корректно определить доверительные интервалы полученных экспериментальных значений вековых смещений, то и использовать, полученные ими данные, для каких то оценок различных физических теорий по крайней мере не совсем корректно. В тоже время и примененные мною выше стандартные статистические методы для определения вековых смещений параметров орбит дают такую большую дисперсию, что тоже не позволяет использовать их для этих целей. Но давайте посмотрим, а что мы можем сделать для уменьшения ошибки в определение вековых смещений параметров орбит с применением типовых статистических методов обработки данных наблюдений. Для примера возьмем данные по Меркурию (у него из всех планет самая большая выборка, например, за 400 лет мы имеем 1660 точек, в то время как, например, для Плутона с момента его открытия пока только одну точку прохождения перигелия). На следующем рисунке Вы видите результаты статистической обработки первичных данных по Меркурию не только для определения самого параметра в функции времени по формулам (1a,2a,3a) и потом определения смещения параметра по формулам (1da, 2da), но и сразу определения вековых смещений параметров по формуламdAlfa=k0 (1d)
dAlfa=k0+k1*dT (2d)
dAlfa=k0+k1*dT+k2*dT^2 (3d)http://ser.t-k.ru/Ris/Merkuriy1.gif (http://modsys.narod.ru/Ris/Merkuriy1.gif )
Здесь для получения формул (1d, 2d, 3d) вся выборка по параметру (угол в перигелии) разбита на интервалы по 50 замеров и получены средние значения параметров в этих интервалах (большие черные кружки), а потом как разности между двумя соседними значениями средних значений в интервалах получены единичные значения вековых смещений параметров (большие красные кружки), которые будут находиться на границе двух соседних интервалов. Таким образом мы получим (1660-N1)/50=33 интервала, где N1 это номер первой точки в выборке от которой мы будем обрабатывать данные, т.е. в программе предусмотрена возможность обрабатывать не всю выборку, а только те данные, которые расположены после точки с номером N1. А количество единичные значения вековых смещений параметров (большие красные кружки) у нас будет N=32, т.е. на единицу меньше чем количество интервалов. И теперь обработав уже эти 32 точки мы получим коэффициенты для уравнений (1d, 2d, 3d) и потом по формуле (4), где у нас N будет равно 32, а не 1660, как для формул (1a, 2a, 3a) мы получим стандарт для вековых смещений. Сравним полученные с доверительной вероятностью 95% по разным формулам значения вековых смещений перигелия Меркурия, которые определены или как неизменные во времени значения или как значения в конкретном году (в примере в 1900 году).
dAlfa (1da) = 572,53 +/- 2*7,87
dAlfa (2da) = 571,34 +/- 2*7,84
dAlfa (1d) = 573,45 +/- 2*7,31
dAlfa (2d) = 571,54 +/- 2*7,10
dAlfa (3d) = 571,10 +/- 2*6,88Как видим предельная ошибка определения векового смещения перигелия Меркурия по разным методикам и по разным уравнениям регрессии примерно одинакова и отдать предпочтение какому то одному полученному значению смещения перигелия практически не возможно, а сами значения смещения хоть и незначительно, но все же отличаются и по этому у меня возникает вопрос какое же из полученных значений ближе к истинному, чтобы его можно было использовать для проверки на адекватность различных физических теорий по этому значению. Правда при более значительном разбросе первичных данных, как это видно у Венеры и Земли, вопрос о том какую методику использовать или формулы (1da, 2da) или формулы (1d, 2d, 3d) не стоит, т.к. там при использование формул (1da, 2da) доверительный интервал полученных вековых смещений получается просто огромным. Но тогда остается вопрос какую из формул (1d, 2d, 3d) использовать для определения вековых смещений. И самое главное насколько все чисто в математическом плане в примененной мною методике для формул (1d, 2d, 3d), а так же если я и в формулах (1a, 2a, 3a) буду использовать не единичные значения из выборки, а средние значения в группах.
Я конечно понимаю, что доверительный интервал в несколько десятков секунд (у Земли и Венеры) это многовато, но зато это достоверная информация с четко заданными интервалами, а не абстрактная информация полученная с использованием теории возмущений с принципиально не известной достоверностью. Кроме того, при использовании предлагаемой мною методики определения смещений по средним значениям параметров в группах есть еще некоторые резервы по уменьшению доверительных интервалов. Например, для внутренних планет можно увеличивать количество данных в группах, а для наружных планет находить количество данных в группах так, чтобы продолжительность этой группы в годах наблюдений точно соответствовала периоду изменения этих параметров (для внешних планет это очень сильно влияет на результат). Но прежде чем заниматься этими тонкостями я бы хотел услышать мнение специалистов о том насколько соответствует принципам статистической обработки данных использование мною средних значений параметров в группах для уменьшения доверительных интервалов, т.к. для Меркурия (смотрите рисунок ниже) используя данную методику и увеличив количество точек в группах до 300 мне удалось даже очень значительно снизить доверительный интервал
dAlfa (1d) = 572,76 +/- 2*1,10
dAlfa (2d) = 571,55 +/- 2*0,65
dAlfa (3d) = 572,12 +/- 2*0,47http://ser.t-k.ru/Ris/Merkuriy2.gif (http://modsys.narod.ru/Ris/Merkuriy2.gif )
Если мы сравним данные для случая dAlfa (3d) с известными до этого экспериментальными данными по смещению перигелия Меркурия, то получается, что все они не попадают даже в доверительный интервал для полученного мною смещения, т.к., например, у Ньюкома (Роузвер) было 575,1 у Данкома (Брумберг) было 575,2 у JPL (сайт JPL) было 577,73 и у Брауэра, Вуркома (Субботин) было 589,1. Таким образом, если с точки зрения теории статистической обработки данных в моей методике нет никаких ошибок, то получается, что все известные экспериментальные данные по смещениям параметров планет нуждаются в пересчете. А до тех пор пока окончательно не выяснится насколько правомерно применение предлагаемой мною методики я пока не буду проводить и вычислительные эксперименты с целью определения скорости распространения гравитации и абсолютной скорости Солнечной системы.
С наилучшими пожеланиями Сергей Юдин.
- Re[2]: Смещение перигелия Меркурия и других планет
(С. Ю. Юдин,
5.03.2008 7:55, 10.1 КБайт)
Наконец-то теоретическое обоснование моей методики обработки экспериментальных данных (наблюдательных и полученных при вычислительном эксперименте на модели) более менее устаканилась (хотя и остались некоторые пробелы) и я решил выложить некоторые полученные результаты для обсуждения. Ранее я уже приводил данные по смещениям перигелиев планет в таблице 4, а сейчас я уберу из нее свои данные, которые получены на модели, и данные НАСА, которые приводил со ссылкой на Хайдарова, т.к. последние отличаются от найденных мною данных НАСА, а конкретно от данных JPL, которая является подразделением НАСА. Но в то же время я и дополню эту табличку данными, полученными мною после обработки первичных данных JPL (из фонда DE405), которые признаются практически всеми именно данными наблюдений. А по причине, о которой я скажу позже, я уберу данные по Юпитеру и Сатурну.
Таблица 4а. Обработанные разными авторами экспериментальные данные наблюдений для определения вековых смещений перигелиев 4-х внутренних планет. В скобках указан источник, откуда взяты уже обработанные данные (у меня данные JPL это исходные данные).
______________Меркурий__Венера__Земля_Марс
JPL (JPL)__________577,7____9,7__1163,8__1599,9
Юдин (JPL)________572,2___37,8__1157,2__1599,5
Ньюком (Роузвер)___575,1___42,5__1162,9__1602,7
Данком (Брумберг)__575,2___34,3__1153,8___---
Брауэр, Вурком _____589,1___---_____---___1800,0
(Субботин)Если не принимать во внимание данные Брауэра и Вуркома, которые я нашел у Субботина, то можно сказать, что, не смотря на разные исходные данные и примененные для этого методики обработки данных наблюдений, результаты у всех авторов получаются практически одни и те же (кроме данных JPL по Венере, но и здесь не все потеряно). Если учесть, что, приведенные значения вековых смещений, JPL рекомендует использовать для расчета параметров орбит в интервале с 1800 по 2050 год, то, наверное, и данные наблюдений для их определения они использовали за этот период, а у всех остальных авторов (насколько я об этом знаю) использованы данные наблюдений примерно с 17-го века. А в этом случае вполне может получить для 2000 года и значение приведенное JPL (у меня, например, в таблице 4 вообще приведено расчетное значение для 2000 года минус 5). Таким образом, можно сказать что, не смотря на некоторые существующие пока теоретические пробелы, моя методика прошла предварительную проверку практикой и, следовательно, ее можно использовать уже сейчас в практической деятельности.
Но прежде чем я перейду к практическому использованию моей методики для сложных расчетов по определению скорости распространения гравитации и абсолютной скорости Солнечной системы я бы хотел не только привести, полученные мною сейчас, после обработки экспериментальных данных наблюдений, предоставленных JPL, значения вековых смещений всех остальных (кроме полуоси эллипса) параметров внутренних планет, но и остановится на некоторых тонкостях определения вековых смещений планет с использованием моей методики. Первым делом я обработал по своей методике данные наблюдений JPL за период с 1.01.1601 года по 1.01.2001 года (использовано 2-а разных фонда DE200 и DE405), а также данные полученные за этот же период при проведение вычислительных экспериментов на разных моделях систем. Вообще то обе модели были чисто Ньютоновскими, но отличались массами планет и начальными параметрами орбит планет, которые задавались или по данным JPL или по данным Ньюкома.
При этом я привожу не только полученные мною значения вековых смещений параметров орбит (AlfaP перигелий, AlfaU узел восхождения, Betta наклон орбиты и Eks эксцентриситет), но привожу и доверительный интервал для этих значений при доверительной вероятности (надежности) 95%. Полученные смещения углов у меня даны в угловых секндах, а безразмерные значения вековых смещений эксцентриситетов увеличены мною в 3600 раз. Шаг численного решения дифференциальных уравнений и обработки данных наблюдений JPL для всех планет был постоянным 3600 с, но при определение угла в перигелии и угла узла восхождения он уменьшался так, чтобы интервал погрешности замера угла в перигелии не превышал одной угловой секунды (например, для Меркурия основной шаг уменьшался в 1000 раз). А при статистической обработке данных я всю выборку полученных данных по параметрам орбит разбивал на 5 групп, вычислял в них средние значения параметра, а затем эти пять точек аппроксимировал линейной зависимостью
Alfa=k0+k1*dT (2a)
а взяв первую производную я получал значения вековых смещений параметров орбит - k1 (если у нас время dT в формулах 2a будет измеряться столетиями). Т.к. многим все эти, полученные мною значения параметров орбит будут не интересны, я прикрепляю их в виде текстового файла таблица11, который можно скачать отсюда http://modsys.narod.ru/Arhiv/tabl11.zip , а здесь приведу только полученные мною данные по 4-м аномалиям, которые обнаружил Ньюком, и о которых мы сейчас и поговорим. Но прежде я сделаю некоторые общие выводы по данным, приведенным в таблице11. Во-первых, радуют довольно маленькие доверительные интервалы получившиеся при обработке данных, а во-вторых, не смотря на столь хорошую точность, значения вековых смещений полученных по фондам DE200 и DE405 почти все совпадают до последней цифры. Таким образом, я, во-первых, в следующей версии программы фонд DE200 уберу, т.к. не вижу, чтобы данные фонда DE405 были, как пишут, гораздо точнее данных фонда DE200 (а для меня более важно, что они не подогнаны под нужный результат), а во-вторых, и данные, полученные на двух разных моделях систем, тоже не очень сильно отличаются друг от друга и, по этому, при предварительном анализе я буду пользоваться только данными, полученными на модели с параметрами JPL, что является оправданным еще и по тому, что и экспериментальные данные у нас имеются пока только предоставленные JPL. А теперь давайте вернемся к аномалиям Ньюкома, где рядом с данными Ньюкома я приведу и полученные мною данные при обработке данных фонда DE405 и полученные на модели с параметрами JPL.
Таблица 12. Аномальные смещения параметров орбит планет.
Параметр_____Наблюдения_______Теория__________Разность
Eks1*dAlfaP1__118,24+/-0,40*___109,76+/-0,16*___8,48+/-0,43*
dAlfaP1______575,06+/-1,95*___533,82+/-0,78*___41,24+/-2,09*
dAlfaP1______572,17+/-0,30____529,38+/-0,31____42,79+/-0,31Eks4*dAlfaP4__149,55+/-0,35*___148,80+/-0,04*___0,75+/-0,35*
dAlfaP4_____1602,69+/-3,75*__1594,65+/-0,43*___8,04+/-3,75*
dAlfaP4_____1599,53+/-6,25___1601,67+/-6,29____2,14+/-6,29sin(Betta2)*dAlfaU2_-105,40+/-0,12*__-106,00+/-0,12*___0,60+/-0,17*
dAlfaU2_________-1780,68+/-2,03*__-1790,81+/-2,03*__10,14+/-2,87*
dAlfaU2__________-998,75+/-1,25___-998,96+/-1,44_____0,21+/-1,44dEks1_______3,36+/-0,50*______4,24+/-0,01*_____0,88+/-0,50*
dEks1_____0,07375+/-0,0010__0,07402+/-0,0011__0,00027+/-0,0011* - здесь Ньюком приводит средние ошибки, но для определения аномальности смещения он использует вероятные ошибки, которые получаются умножением средних ошибок на 0,67454. Вот только я нигде не нашел для какой доверительной вероятности (надежности) он приводит эти вероятные ошибки, а без указания доверительной вероятности все эти вероятные ошибки не несут никакой информации.
В приведенных выше данных, первая строка (или две первых) это данные Ньюкома, а последняя строка это мои данные. Обозначения вековых смещений параметров орбит соответствуют принятым в моей программе Solsys5 и в вышеприведенной таблице11 (AlfaP перигелий, AlfaU узел восхождения, Betta наклон орбиты и Eks эксцентриситет), а последняя цифра соответствует порядковому номеру планеты. Я уже писал о том, что Ньюком не всегда пользовался общепринятыми формулами, но приведенные в этой таблице его данные ставят меня просто в тупик. Что касается смещений перигелия, то здесь все понятно, и он дает, как это обычно делают при определение смещений перигелия с использованием теории возмущений, произведение эксцентриситета орбиты на смещение перигелия Eks*dAlfaP, что я элементарно перевожу в само смещение dAlfaP. А вот перевод произведения синуса угла наклона орбиты на смещение узла восхождения sin(Betta2)*dAlfaU2 для Венеры, у меня дает цифры очень отличающиеся от цифр, которые я получаю непосредственно замеряя угол восхождения в моей программе dAlfaU2 и я буду признателен всем, кто поможет мне с этим казусом разобраться. Ну и совсем я не понимаю почему у Ньюкома смещение эксцентриситета дано в угловых секундах. Правда, если он его определял как изменение параллакса орбиты, то тогда вроде все нормально и можно использовать и эти его значения для выводов об аномальности этого смещения, но если нет, то опять возникает вопрос.
Хорошо, пусть будем считать, что все эти казусы нами успешно разрешены и доверительная вероятность у Ньюкома никак не меньше 95%. Все равно ничего хорошего в этом случае у нас не получается и из 4-х аномалий Ньюкома я вижу по своим данным только одну аномалию для перигелия Меркурия. А аномального смещения узла восхождения у Венеры, перигелия Марса и эксцентриситета у Меркурия я не вижу, т.к., при заданной мною доверительной вероятности, полученные доверительные интервалы для этих параметров перекрывают и без того микроскопическую разницу в полученных мною наблюдаемых и расчетных значениях. Хотя, вот у Земли впору уже говорить об аномальном смещение перигелия, т.к. доверительные интервалы наблюдаемых и расчетных значений с большим трудом перекрывают друг друга. Априори будем считать, что у Ньюкома с полученными данными все более-менее в порядке и тогда остается только подумать, что мы можем сделать при обработке данных полученных мною на математической модели и из фонда DE405 (если там у JPL тоже все в порядке). И через пару дней я постараюсь что ни-будь придумать в этом направление и доложу свои соображения, а то получается, что, после приведенных мною данных, ОТО вообще может спать спокойно, т.к. ни смещение узлов Венеры, ни смещение эксцентриситета Меркурия ей теперь объяснять не надо. Да и небольшая проблема с перигелием Марса у нее тоже отпала.
С наилучшими пожеланиями Сергей Юдин.
- Re: Смещение перигелия Меркурия и других планет
(М. Г. Мумов,
6.03.2008 12:27, 1.9 КБайт, ответов: 34)
Как показано в теме И. А. Амплеева -Движение тел в Пространстве(логика современных данных)- здесь, на форуме, в данном разделе, а также на его сайте, траекторией движения космических тел во Вселенной являются винтовые линии.
В этой связи, траекторией движения Солнца во Вселенной является - винтовая же линия, которая накладывается на винтовую же линию траектории движения во Вселенной Центра нашей галактики.
А вот траектории планет солнечной системы также есть винтовые линии... которые накладываются на траекторию движения Солнца во Вселенной, повторю - по винтовой линии же.
Между тем, в силу того, что Солнце движется по винтовой линии, то вектор скорости его движения - постоянно меняется. Имеется ввиду - каждый год, каждый день, каждый час, каждую секунду.
Каждый век, тысячелетие, миллионолетие, миллиардолетие.
Земные.
А вот перигелии планет солнечной системы - обязаны находиться - по курсу движения Солнца; движения Солнца- по его винтовой линии.
И что характерно - они и бывают - там, где они обязаны находиться. Перигелии.
Иначе - они обязаны смещаться. И - без сомнений - смещаются.
Обращу внимание, что планеты в точке перигелия находятся не ежесекундно, не ежечасно, не ежедневно, но - раз в свой год.
Ну, и показанным выше и объясняется факт смещения перигелия планет.
Авот - потуги - автора темы... напоминают, хотя бы, потуги незадачливого охотника за мёдом диких пчёл, который, чтобы обнаружить дупло в дереве, в котором улей находится... рубит даже и не дерева... не в целом в каком-то лесе, а прям всю тайгу, к примеру - сибирскую... по принципу - авось путём подобного и выйду на физический смысл существа - этого самого смещения перигелиев планет.
С прискорбием, Мусафаил Мумов, учащийся 11-го класса.
- Re[2]: Смещение перигелия Меркурия и других планет
(С. Ю. Юдин,
7.03.2008 16:30, 2.8 КБайт, ответов: 33)
< tbody>
Цитата: Как показано в теме И. А. Амплеева -Движение тел в Пространстве(логика современных данных)- здесь , на форуме, в данном разделе, а также на его сайте, траекторией движения космических тел во Вселенн ой являются винтовые линии.
Ну, и показанным выше и объясняется факт смещения пери гелия планет.
С прискорбием, Мусафаил Мумов, учащийся 11-го класса.
Вообще-то один изобретатель (Т.Г. Архангельски й) мне уже сообщал об этом открытии и даже запатентовал его (смотрите сообщение от 27.11.200 7). Таким образом И. А. Амплеев со своим открытием опаздал, а т.к., Вы учитесь пок а только в 11 классе, надеюсь, что Вы еще успеете сделать свое открытие, вместо того, чтобы п ропогандировать в Интернете чужие открытия, в сути которых Вы плохо разбираетесь (есл и конечно же Вы это делаете просто от безграмотности, а если э то клиника, то мы конечно же увидим бесчисленное множество Ваших гениальных открытий). Хочет ся надеяться на перв ое, а то вот И. А. Амплеев уже записал Вас в больные и ответил Вам "Доктор на больного не обижается!" .
Сергей Юдин.
Астронет | Научная сеть | ГАИШ МГУ | Поиск по МГУ | О проекте | Авторам Комментарии, вопросы? Пишите: info@astronet.ru или сюда Страницы спонсоров: Строительное об орудование группа компаний Альфа-Сервис, Москва | KINO.RU - фильмы, кино театры, кино, ра списание кино в г. Москва | загородная недвижимость Penny Lane. незадачливого охотника за мёдом диких пчёл, который, чтобы обнаружить дупло в д еве, в котором улей находится... рубит даже и не дерева... не в целом в каком-то лесе, а прям всю тайгу, к примеру - сибирскую... по принципу - авось путём подобного и выйду на ф ический смысл существа - этого самого смещения перигелиев планет.С приск рбием, Мусафаил Мумов, учащийся 11-го класса.
- Re[3]: Смещение перигелия Меркурия и других планет
(М. Г. Мумов,
9.03.2008 19:43, 1.8 КБайт, ответов: 32)
Цитата: т.к., Вы учитесь пока только в 11 классе,
На ФИАНовском форуме, http://phorum.lebedev.ru/, два года тому назад, я тогда в 9-м классе учился, тамошним СП мною давались пояснения насчёт их возраста и моего.
Там у меня ник "mumu", по первым двум буквам имени и фамилии.
Коротко суть следующая: Библейский персонаж Мусафаил, в честь кого меня назвали, жил девятьсот лет.
А в нашем роду люди тоже живут подолгу, чуть не все до 90, как минимум. Поэтому я беру коэффициент 1 : 10 = 90 : 900.
То есть, хотя мне и семнадцать, но Вы можете считать, что мне в десять раз больше, а именно: 170.
Так, вот И. А. Амплееву сейчас 66, и вряд ли он касательно видения мира достигнет того, что я знаю.
Однако, можно посчитать, что мне всё-таки семнадцать, а ему с коэффициентом 10 будет только 6,6 лет. То есть, он ещё не читать, не писать не умеет. Не страшно, авось да научится.
Так, а у Вас, Сергей Юдин, с этим коэффициентом возраст-то каков?3,5 годика? Вы ещё в ясли ходите, и на горшок сами не садитесь, нянечка усаживает? И попу вытирает?
Вам дали объяснение истинной причины того,на что физики всего мира не могли дать истинного объяснения полтора века.
И объяснение это основывается на той позиции, которую отстаивает И. А. Амплеев.
Потому как эта позиция, что космические тела движутся по винтовым линям, и есть истина.
Вам не понятны ни объяснение истинной причины смещения перегилиев планет, ни то, что космические тела движутся по винтовым линиям?
- Re[4]: Смещение перигелия Меркурия и других планет
(С. Ю. Юдин,
10.03.2008 9:18, 1.5 КБайт, ответов: 31)
mumu //То есть, хотя мне и семнадцать, но Вы можете считать, что мне в дес ять раз больше, а именно: 170.//
К сожалению, диагноз И. А. Амплеева о В ашем заболевании подтвердился. По этому, не зависимо от Вашего возраста, я поступлю с Вами также как и со всеми остальными невменяемыми с обеседниками в Интернете, т.е. просто перестану Вас замечать. Таким образ ом, можете не утруждать себя дальнейшей писанин ой, т.к. отвечать на Ваши послания я не буду.
Желаю наискорейшего выздоровле ния. Сергей Юдин.
Астронет | На учная сеть | ГАИШ МГУ | Поиск по МГУ | О проекте | Авторам Комментарии, вопросы? Пишите: info@astronet.ru или сюда Страницы спонсоров: Строител ьное оборудование группа компаний Альфа-Сервис, Москва | KINO.RU - фильмы, кино театры, кино, расписание кино в г. Москва | загородная недвижимость Penny Lane. - Re[5]: Смещение перигелия Меркурия и других планет
(С. Ю. Юдин,
11.03.2008 15:01, 9.1 КБайт, ответов: 30)
В предыдущем сообщение в таблице 11 я привел полученные мною данные смещений параметров орбит, когда я всю выборку первичных данных, т.е. параметров орбит полученных при каждом обороте планеты, разбивал на 5 групп, затем внутри группы вычислялял 5 средних значений в группах и аппроксимировал эти 5 точек линейной зависимостью. А дифференцируя это уравнение по времени я находил вековые смещения параметров орбит, но, как показало дальнейшее исследование этого вопроса, это оказалось не лучшим решением. Взгляните на нижеприведенный рисунок, где вычисляются вековые смещения перигелия Меркурия и определяются доверительные интервалы этого смещения при различном количестве точек (оборотов планеты) в группе, где по оси абсцисс отложено количество точек в группе в масштабе 10 точек/см.
http://ser.t-k.ru/Ris/Merkuriy4.gif (зеркало http://modsys.narod.ru/Ris/Merkuriy4.gif)
Как видим (особенно на нижнем рисунке, где доверительные интервалы совмещены и даны при другом масштабе), при примерно постоянном значение самого смещения доверительные интервалы с увеличением количества точек в группах уменьшаются, но уменьшаются не равномерно, а с явной цикличностью. По этому взятое наугад значение количества точек в группе, чтобы получилось 5 групп, как я это делал раньше, может нам дать примерно одинаковое значение матожидания, но дисперсия может оказаться в несколько раз больше, чем в случае, если мы возьмем на несколько точек в группе больше или меньше. По этому, нам желательно выбрать для расчета количество точек, при котором дисперсия циклически достигает минимума, но какой именно минимум из множества взять и насколько будет достоверен такой результат не ясно.
Можно просто в режиме автопоиска найти количество точек в группе, т.е. оборотов планеты, когда дисперсия будет минимальной, что по идее должно соответствовать периоду времени, когда все наиболее значимые гармоники периодических возмущений будут кратное число раз укладываться в этом периоде. Но я не считаю такой подход гарантией наиболее точного результата по определению вековых смещений и аномальных остатков этих смещений, т.к., как будет видно из данных таблицы 13, при обработке данных наблюдений и расчетных данных минимальная дисперсия в одном случае получается при одном количестве точек, а в другом случае при другом (хотя иногда эти периоды и совпадают). Это говорит о том, что у нас имеются погрешности в определение первичных наблюдательных или полученных на модели расчетных данных и по этому остается вероятность, что полученное таким образом значение будет менее достоверным, чем требуемое нам значение доверительной вероятности 95%.
А можно и не заморачиваться со всем этим, а просто посчитать среднее значение матожидания из получившихся у нас 554 значений, т.е. по всем возможным группам точек для расчета средних значений в группе (для Меркурия, у которого выборка состоит из 1664 точек, у нас, если учесть, что минимальное количество групп должно быть равно трем, получается, что количество точек в группе может быть от 1-ой до 554-х). Но возникает вопрос, а как быть с доверительными интервалами, т.к. при таком простом подходе можно находить только средние значения самих параметров, а не квадратных корней из разности квадратов. И у нас, как видно из сравнения с данными из таблицы 13, полученными при других подходах, получаются просто запредельные значения доверительных интервалов (напримр, для перигелия Меркурия +\- 0.843, а для перигелия Венеры +/- 62,133). По этому в таблице 13 я для средних значений вековых смещений параметров, рассчитанных таким образом, привожу доверительные интервалы, рассчитанные по самим значениям матожиданий, т.е. для Меркурия как удвоенную (для доверительной вероятности 95%) дисперсию 554 матожиданий.
Хотя в принципе, т.к., по большому счету, для определения аномальности нас интересует не само значение смещения, а только разность между наблюдаемым и расчетным значением, можно посчитать и среднюю разность между соответствующими матожиданиями всех полученных значений, но каков будет при этом доверительный интервал это еще более сложный вопрос, чем при расчете средних матожиданий. А, как видно из приведенных мною выше данных в таблице 4в, для определения аномальности в наблюдаемых и расчетных значениях величина доверительных интервалов для нас так же важна, как и сами матожидания вековых смещений. По этому данные, полученные таким образом, я в таблице 13 не привожу. Тем более, что само значение смещения будет таким же как и при разности между средними значениями наблюдаемых и расчетных величин, но я не отказываюсь от этого приема, т.к. он может оказаться очень полезен для внешних планет, у которых маленькие выборки данных.
А вот наиболее перспективным, для определения матожидания и доверительных интервалов из всех имеющихся значений (для Меркурия из 554), я считаю использование метода максимина (минимакса) для нахождения границ доверительных интервалов, по которым потом мы и определяем матожидание. Т.е. я передлагаю найти минимально возможный интервал значений вековых смещений параметров при котором все полученные интервалы хотя бы примыкают (а еще лучше пересекаются), к этому интервалу. Если кто-то не знаком с этими критериями минимакса и максимина, которые обычно используются в теории игр при выборе оптимальных стратегий, т.е. для нахождения наилучшей из наихудших стратегий, я сейчас поясню о чем идет речь на примере нахождения доверительного интервала для смещения перигелия Венеры по данным DE405. На нижеприведенном рисунке Вы видите посередине рисунка синюю ломаную линию, которая отражает изменение матожидания с увеличением количества точек в группе от 1 до 217 для расчета средних значений параметра в группе, т.е. до максимально возможного количества точек из выборки в 651 точку (как и раньше в 1см 10 точек). А сверху и снизу Вы видите синие ломаные линии, которые показывают верхнюю и нижнюю границы доверительного интервала полученного при этом значении смещения параметра.
http://ser.t-k.ru/Ris/Venera2.gif (зеркало http://modsys.narod.ru/Ris/Venera2.gif)
При обработке данных по перигелию Венеры мы получили 217 значений матожидания смещения перигелия и 217 доверительных интервалов, но наименьшее значение доверительного интервала мы получили в том случае, когда у нас в группах было 197 первичных данных положения перигелия. Вот этот доверительный интервал мы и берем за исходный. А теперь сравниваем все остальные доверительные интервалы с этим таким образом, чтобы значения смещения в этом интервале хотя бы частично перекрывались всеми остальными. Вплоть до группы из 177 точек у нас это условие соблюдается, но при 177 точках мы имеем доверительный интервал от 34,834 до 39,302, который не соприкасается своей верхней границей с нижней границей минимального интервала при 197 точках, который имеет границы от 39,605 до 40,717. По этому опускаем немного нижнюю границу минимального интервала до верхней границы интервала при 177 точках. Теперь уже этот интервал сравниваем со всеми остальными и видим, что при 187 точках (от 44,710 до 45,994) мы имеем нижнюю границу интервала расположенную выше верхней границы максиминного интервала. Поднимаем верхнюю границу максиминного интервала до 44,710. Далее мы находим, что верхняя граница интервала при 210 точках (от 34,104 до 37,746) находится немного ниже нашей нижней границы максиминного интервала, по этому опускаем нижнюю границу максиминного интервала до 37,746. Окончательно получаем максиминный интервал (две горизонтальные синие линии) от 37,746 до 44,710. Отсюда находим матожидание 41,228.А теперь давайте обработаем первичные данные, как наблюдений из фонда DE405 (JPL), так и полученные на математической модели (опять таки с параметрами орбит, рекомендуемыми JPL) по моей методике, а потом определим из всех возможных значений смещений параметров орбит и доверительных интервалов этих смещений итоговые значения матожидания и доверительных интервалов по трем предложенным мною только что критериям. Напоминаю, что 1-ый критерий по минимальному доверительному интервалу, 2-ой критерий по максиминному доверительному интервалу и 3-ий критерий - для матожидания по среднему значению из всех полученных, а для доверительных интервалов для 3-го критерия из дисперсии всех матожиданий. Затем, по полученным значениям, мы определим аномальные остатки, т.е. величину наблюдаемых вековых смещений не объясняемую только теорией Ньютона, и все это оформим в виде таблицы 13, где также как и в таблицах 11 и 12 у меня приняты следующие обозначения вековых смещений параметров орбит (AlfaP перигелий, AlfaU узел восхождения, Betta наклон орбиты и Eks эксцентриситет), а числовой индекс в конце соответствует порядковому номеру планеты. Полученные смещения углов у меня даны в угловых секндах, а безразмерные значения вековых смещений эксцентриситетов увеличены мною в 3600 раз. При этом доверительные интервалы для значений смещений параметров орбит даны при доверительной вероятности (надежности) 95%.
Смотрите продолжение - Re[6]: Смещение перигелия Меркурия и других планет
(С. Ю. Юдин,
11.03.2008 15:05, 10.0 КБайт, ответов: 29)
продолжение
Таблица 13. Наблюдаемые и расчетные значения вековых смещений параметров орбит планет и их разность, когда расчетные значения получены при использование модели, функционирующей только по законам Ньютона. Значения определялись по следующим критериям sr- по средним значениям, min- по минимальному интервалу, maxmin- по максиминному интервалу. После обозначения параметра по критерию min указано число оборотов планеты при обработке первичных данных, при котором это значение получено. Данные обрабатывались за период с 1601 по 2001 годы.Параметр________Наблюдения_DE405__Теория_Ньютон_JPL____Разность
dAlfaP1sr__________572,172+/-0,041__529,090+/-0,041__+43,082+/-0,041
dAlfaP1min_522_500_572,179+/-0,000__529,184+/-0,004__+42,995+/-0,004
dAlfaP1maxmin______572,205+/-0,064__529,119+/-0,068__+43,086+/-0,068dAlfaP2sr____________37,633+/-2,567___29,563+/-2,533___+8,07+/-2,567
dAlfaP2min_197_168__40,161+/-0,556___31,747+/-0,044___+8,414+/-0,556
dAlfaP2maxmin_______41,228+/-3,482___31,831+/-3,060___+9,397+/-3,482dAlfaP3sr__________1159,265+/-1,91__1136,545+/-1,857__+22,720+/-1,91
dAlfaP3min_131_117_1157,632+/-0,57__1135,511+/-0,258__+22,121+/-0,57
dAlfaP3maxmin_____1157,632+/-0,57__1136,127+/-3,008__+21,501+/-3,008dAlfaP4sr_________1599,528+/-1,211__1598,373+/-1,238__+1,155+/-1,238
dAlfaP4min_59_59__1600,286+/-0,166__1598,997+/-0,265__+1,289+/-0,265
dAlfaP4maxmin____1600,228+/-2,037__1599,151+/-2,089__+1,077+/-2,089
---------------------------------------------------------------
dAlfaU1sr__________-450,174+/-0,077__-450,768+/-0,076__+0,594+/-0,077
dAlfaU1min_418_419_-449,953+/-0,492__-450,553+/-0,409__+0,600+/-0,492
dAlfaU1maxmin______-449,953+/-0,492__-450,553+/-0,409__+0,600+/-0,492dAlfaU2sr__________-998,640+/-0,118__-999,643+/-0,131__+1,003+/-0,131
dAlfaU2min_163_163_-998,320+/-0,433__-999,287+/-0,324__+0,967+/-0,433
dAlfaU2maxmin______-998,320+/-0,433__-999,287+/-0,324__+0,967+/-0,433dAlfaU3sr*__________-868,52+/-13,53___-1466,88+/-21,4__+598,37+/-21,4
dAlfaU3min*_48_44___-871,81+/-2,37___-1443,43+/-8,15___+571,62+/-8,15
dAlfaU3maxmin*_____-874,06+/-21,01___-1443,43+/-8,15__+569,37+/-21,01dAlfaU4sr_________-1051,738+/-0,554__-1074,063+/-0,63__+22,325+/-0,63
dAlfaU4min_54_54__-1050,233+/-3,201__-1072,368+/-3,82__+22,135+/-3,82
dAlfaU4maxmin_____-1050,233+/-3,201__-1072,368+/-3,82__+22,135+/-3,82
-------------------------------------------------
dBetta1sr_________-21,4362+/-0,0011_-21,5200+/-0,0014_+0,0838+/-0,0014
dBetta1min_489_421_-21,4355+/-0,000__-21,5181+/-0,000__+0,0826+/-0,000
dBetta1maxmin____-21,4369+/-0,0027__-21,5206+/-0,0025_+0,0837+/-0,0027dBetta2sr_________-2,5858+/-0,0295__-2,8471+/-0,0295__+0,2613+/-0,0295
dBetta2min_163_163_-2,5016+/-0,0215__-2,7626+/-0,2186__+0,261+/-0,2186
dBetta2maxmin______-2,5016+/-0,0215__-2,7626+/-0,2186__+0,261+/-0,2186dBetta3sr__________-47,163+/-0,009___-47,050+/-0,010___-0,113+/-0,010
dBetta3min_94_94___-47,181+/-0,029___-47,073+/-0,038___-0,108+/-0,038
dBetta3maxmin______-47,181+/-0,029___-47,073+/-0,038___-0,108+/-0,038dBetta4sr_________-28,9927+/-0,021__-29,5988+/-0,0204__+0,6061+/-0,021
dBetta4min_55_55__-28,9421+/-0,1145__-29,5494+/-0,123__+0,6073+/-0,123
dBetta4maxmin_____-28,9421+/-0,1145__-29,5494+/-0,123__+0,6073+/-0,123
----------------------------------------------------------
dEks1sr__________0,07376+/-0,00012_0,07396+/-0,00011_-0,00020+/-0,00012
dEks1min_538_507_0,07368+/-0,00001_0,07395+/-0,00001_-0,00027+/-0,00001
dEks1maxmin_____0,07365+/-0,00027__0,07400+/-0,00016_-0,00035+/-0,00027dEks2sr_________-0,17411+/-0,00027_-0,17693+/-0,00028_+0,00282+/-0,00028
dEks2min_170_215_-0,1739+/-0,00007_-0,17623+/-0,00007_+0,00233+/-0,00007
dEks2maxmin_____-0,17400+/-0,00039_-0,17674+/-0,00058_+0,00274+/-0,00058dEks3sr_________-0,15068+/-0,00046__-0,15260+/-0,0005__+0,00192+/-0,0005
dEks3min_117_128_-0,15066+/-0,0001__-0,15236+/-0,0001__+0,00170+/-0,0001
dEks3maxmin_____-0,15077+/-0,0004__-0,15250+/-0,00023__+0,00173+/-0,0004dEks4sr_________0,33070+/-0,00178__0,34363+/-0,00183__-0,01293+/-0,00183
dEks4min_58_62__0,32849+/-0,00076__0,34643+/-0,00005__-0,01794+/-0,00076
dEks4maxmin_____0,32907+/-0,00134__0,34438+/-0,00209__-0,01531+/-0,00209
*- данные обрабатывались с 1601 по 1751 годы, т.к. при приближение к эклиптике эпохи, вследствие очень маленького угла наклона орбиты, смещение узлов на модели начинало стремительно расти.Как Вы уже заметили полученные мною значения аномальных остатков во многом отличаются от общеизвестных данных, но из этого никоим образом не следует, что они не верны. Я бы даже сказал наоборот данные, полученные с использованием моей методики обработки данных наблюдений, более точны, чем данные, полученные с использованием методики, базирующейся на теории возмущений, т.к. моя методика позволяет получать данные для вековых смещений параметров орбит с заданной надежностью (в вышеприведенной таблице надежность равняется 0,95) и по этому говорить о том, что они верны или не верны не имеет смысла. Они верны на 95%. Другое дело, что данная надежность получается при обработке средних значений параметров для конкретного числа оборотов планеты взятых для расчета средних значений в группе и здесь наблюдается некоторая неопределенность, т.к. при разном количестве точек в группе получаются все-таки разные результаты. Но я считаю, что предложенный мною критерий максимина позволяет убрать эту неопределенность, хотя и с незначительным уменьшением надежности полученных данных, и по этому его можно использовать для принятия решения о том является ли разность между полученными данными наблюдений и теоретическими данными, полученными на Ньютоновской модели Солнечной системы, аномальным остатком, т.е. остатком, не объясняемым теорией Ньютона. И сейчас я с использованием этого критерия приведу сводную таблицу по всем остаткам, полученным с использованием этого критерия. А после того как я в следующей версии программы дополню первичные данные еще и противоположными точками, определяющими положение линии узлов и линии аспид, точность полученных данных значительно улучшиться, т.к. чем больше выборка тем у нас получается меньше дисперсия вековых смещений.
Таблица 14. Разность между наблюдаемыми и расчетными значениями вековых смещений параметров орбит планет по данным таблицы 13, определенная с использованием максиминного критерия.
___________Меркурий_______Венера_________Земля________Марс
dAlfaP____+43,09+/-0,07___+9,40+/-3,48___+21,50+/-3,01___+1,08+/-2,09
dAlfaU____+0,60+/-0,492__+0,967+/-0,433__+569,4+/-21,0___+22,14+/-3,82
dBetta___+0,084+/-0,003__+0,261+/-0,219__-0,108+/-0,038__+0,607+/-0,123
dEks_-0,00035+/-0,00027_+0,0027+/-0,0006_+0,0017+/-0,0004_-0,015+/-0,003Как мы видим, по данным этой таблицы, из 4-х аномалий Ньюкома у нас осталась только одна аномалия по перигелию Меркурия, но зато у нас появились новые аномалии. И если теперь у ОТО Эйнштейна, если посмотреть на уточненную табличку 3а, нет проблем с аномальным смещением перигелиев Венеры и Марса, которые были по данным Ньюкома, то появилась новая проблема - аномальное смещение перигелия Земли, которое очень отличается от того, что дает ОТО.
Таблица 3а. Аномальные остатки смещения перигелиев планет, которые не объясняются теорией Ньютона
________________________Меркурий___Венера___Земля___Марс
остаток Ньюкома (Эйнштейн)__41,24____-7,33_____5,97_____8,04
остаток Данкома (Субботин)___43,1______8,36_____5,01_____1,07
остаток Юдина-JPL (Юдин)____43,1______9,4______21,5_____1,08
ОТО Эйнштейна (Субботин)___43,0_______8,6______3,8______1,4А, если учесть, что ОТО никак не объясняет (насколько мне известно) аномальные смещения линии узлов, углов наклона орбит и их эксцентриситетов, которых по данным таблицы 14 предостаточно, то надо сказать, что у ОТО появились большие проблемы с ее экспериментальным подтверждением. Хотя, возможно, что ОТО не может объяснить эти аномалии и по чисто техническим причинам, т.е. просто из-за невозможности получить аналитическое решение данной задачи, но тогда пусть сторонники ОТО позаботятся о численном решение этой задачи, т.е. создадут математическую модель Солнечной системы в соответствие со всеми требованиями ОТО и получат на ней все вековые смещения параметров орбит совпадающие с наблюдаемыми данными. Или пусть хотя бы дадут мне основные уравнения, вытекающие из ОТО, а я оформлю их в виде модели, прогоню на ней вычислительные эксперименты и обработаю их по своей методике. Только не надо мне давать уравнений, которые получаются при решение первой задачи динамики (обратной задачи), т.е. по известной траектории находятся силы, которые необходимо приложить к телу, чтобы оно двигалось по этой траектории, как это сделал Сергей Хартиков. Естественно, что в этом случае, если мы приложим к телу эти силы, оно и будет двигаться по нужной нам траектории. Вот только мы не всегда в этом случае сможем объяснить откуда взялись эти силы, т.е. это будет похоже на обычный фокус.
Надеюсь, что кто-то займется все-таки этим вопросом и даст мне формулы непосредственного определения сил для решения второй (прямой) задачи динамики. Конкретно мне надо выражение для гравитационного потенциала в любой точке пространства по которому я определю и силу притяжения между Солнцем и планетой и замедление темпа времени в этой точке пространства. А я пока попробую в первом приближение определить абсолютную скорость Солнца и распространения гравитации только по аномальному смещению перигелия Меркурия, учтя в Ньютоновской модели Солнечной системы скорость распространения гравитации. Вообще-то программа позволяет это делать сразу по всем показателям всех планет по единому критерию оптимизации, который определяется с учетом весовых коэффициентов параметров, но пока я считаю это преждевременным и продолжаю надеяться, что найдутся какие-то другие эфемериды, отличные от эфемерид JPL, чтобы уточнить полученные мною данные, а то доверяться одному источнику первичных данных я не привык.
С наилучшими пожеланиями Сергей Юдин.
- Re[7]: Смещение перигелия Меркурия и других планет
(В. В. Чазов,
12.03.2008 17:55, 1.3 КБайт, ответов: 28)
Дорогие друзья, проба пера. Даже ежели и неудачная, даже ежели не окажусь тем самым кто-
то, то не буду огорчён.
Надеюсь, что кто-то ... даст мне формулы непосредственного определения сил для решения второй (прямой) задачи динамики
В оригинальной публикации Е.Майлса Стэндиша и Джеймса Г.Вильямса сказано так:
3.1. Взаимодействие точечных масс
Для каждого небесного тела i ускорение, обусловленное взаимодействием точечных масс, даётся уравнением
С поклоном, Ваш Вадим, но какого типа это выражение, первого или второго, судить не мне. - Re[8]: Смещение перигелия Меркурия и других планет (С. Ю. Юдин, 13.03.2008 19:07, 769 Байт, ответов: 27) Вадим, вообще-то это именно то, что мне надо. Вот только не понятно зачем здесь присутствует последний член, да и расшифровка всех обозначений нужна подробная. Будут конечно проблемы со второй производной Rj , но современная техника позволяет их более менее решать. У меня к Вам просьба отсканировать все, что связано с этой формулой или еще лучше дать ссылку на эту книжку. P.S. А Вы что хотели вставить рисунок со своей странички на narod.ru что ли. Вообще то с этого сайта этот номер не пройдет. Я всегда, когда вставляю рисунки в сообщения, вставляю рисунки со своей домашней странички, имеющей прямой доступ из сети, а не со странички на narod.ru, где скачивание файлов делается через промежуточную форму. С наилучшими пожеланиями Сергей Юдин.
- Re[9]: Смещение перигелия Меркурия и других планет
(В. В. Чазов,
14.03.2008 11:27, 1.4 КБайт, ответов: 26)
Дорогие друзья, уважаемый Сергей. Простите великодушно, с формулой получилось неудачно,
без обращения к страничке ...narod.ru изображение imfor301.gif на нашем формуле не
появляется.
Формула опубликована учёными США в 1972 году. В общем виде она приспособлена почти для всех релятивистских моделей, в том числе и ОТО.
Сегодня день рождения Альберта Эйнштейна, о чём нам любезно напомнил Михаил Евгеньевич, спасибо и ему и мудрому Альберту.
Для различных релятивистских моделей в этой формуле используют различные числовые значения коэффициентов β и γ. Учёные лаборатории реактивного движения применяют постоянные ОТО: β=1 и γ=1.
Уравнения движения записаны для девяти планет, Луны и Солнца относительно центра масс Солнечной системы. Индексы i и j изменяются от 1 до 11. Обозначения для векторов r- полужирный шрифт. Буквой v обозначен модуль скорости. Вторую производную от расстояния r специально вычислять не надо, она появляется автоматически в левой части уравнения.
Последние два слагаемых суммы обусловлены притяжением малых планет. Сумма от 1 до 3 - влияние трёх самых массивных астероидов. Во второй сумме ускорение F обусловлено влиянием 297 малых тел трёх таксономических классов c, s, m, выбранных специальным образом из общей совокупности.
Yours ever, Vadim. - Re[10]: Смещение перигелия Меркурия и других планет
(В. В. Чазов,
14.03.2008 14:39, 729 Байт, ответов: 25)
Дорогие друзья.
Простите великодушно, привычная уже работа над ошибками.
В конце первого абзаца вместо "на нашем формуле не появляется" следует читать "на нашем форуме не появляется".
В третьем абзаце в имени собственном "Учёные лаборатории..." имелось в виду "Учёные лаборатории...".
Небольшое добавление.
В той формуле, что не видна на нашем форуме, буква c не что иное, как скорость света.
Публикация сэра Е.Майлса Стэндиша и мистера Джеймса Г.Вильямса размещена в формате PDF (233282 bytes) на страничке комиссии 4 (Эфемериды) Международного астрономического союза.
С поклоном, Ваш Вадим. - Re[11]: Смещение перигелия Меркурия и других планет
(С. Ю. Юдин,
15.03.2008 9:06, 971 Байт, ответов: 24)
Вадим, во-первых, большое спасибо за ссылку на статью //Орбитальные эфемериды Солнца, Луны и планет//, где приведена формула, которую Вы не смогли загрузить на этот сайт (сейчас попробую я)
[img]http://ser.t-k.ru/Ris/....gif[/img] (зеркало http://modsys.narod.ru/Ris/....gif)А во-вторых, у меня к Вам будет просьба прокомментировать эту статью в свете того на сколько данные в файле DE405 являются результатом обработки данных наблюдений за планетами, а на сколько обработки данных вычислительного эксперимента проведенного на модели Солнечной системы, которая построена с использованием приведенной формулы. Что касается данных после 2000 года, то это ясно чисто расчетные данные, а вот с 1600 по 2000 год данные могут быть и чисто расчетными и чистыми данными наблюдений и данными наблюдений откорректированными расчетными данными (или наоборот).
С наилучшими пожеланиями Сергей Юдин.
- Re[12]: Смещение перигелия Меркурия и других планет
(С. Ю. Юдин,
15.03.2008 9:39, 161 Байт, ответов: 23)
Без htm кода фокус не получился. Попробуем с кодом


- Re[13]: Смещение перигелия Меркурия и других планет
(С. Ю. Юдин,
15.03.2008 9:46, 491 Байт, ответов: 22)
Написал и так
<p><img src="http://ser.t-k.ru/Ris/....gif" width="620" height="440"></p>и так
<img width="620" height="440" src="http://ser.t- k.ru/Ris/....gif" />но не получилось задать даже размер картинки. Вадим какой код писали Вы.
С наилучшими пожеланиями Сергей Юдин. - Re[14]: Смещение перигелия Меркурия и других планет
(В. В. Чазов,
15.03.2008 15:44, 1.2 КБайт, ответов: 21)
Здравствуйте, Сергей. Перевод статьи авторов современных эфемерид обязательно закончу.
Данные по наблюдениям планеты Меркурий следующие. Были использованы только ряды радиолокационных наблюдений:
радиотелескоп Аресибо, с 1967 по 1982 годы, средняя квадратическая погрешность одного измерения 10 км,
радиотелескоп Хайстак, с 1966 по 1971 годы, погрешность одного измерения 1.5 километра,
Голдстоун, 1970-1977 годы, 1.5 км.
С наблюдениями Венеры дело обстоит примерно также.
Для каждой планеты методом наименьших квадратов на основе наблюдений были улучшены начальные условия (вектор положения и вектор скорости) на выбранный момент времени (в середине 1969 года). Но было конечное множество и других параметров, топография поверхности Меркурия, например.
Но, дорогие друзья, могу ошибаться. Если Вы поправите, будет хорошо. Да и сам посмотрю свежие данные. Учёные Лаборатории реактивного движения не обязаны сообщать нам всё, что знают.
Будучи любознательным, кодировку различных страниц в Интернете разглядываю с помощью главного меню браузера: Вид (View)-> В виде HTML (HTML code).
С поклоном, Вадим. - Re[15]: Смещение перигелия Меркурия и других планет
(С. Ю. Юдин,
15.03.2008 17:00, 189 Байт, ответов: 20)
Посмотрел код и не понял, куда в нем делось название самого рисунка, т.к. вместо него только пи-пи-пи. Сейчас попробую еще раз.

- Re[16]: Смещение перигелия Меркурия и других планет
(С. Ю. Юдин,
15.03.2008 17:04, 438 Байт, ответов: 19)
Не понял. Ведь в режиме просмотра картинка была видна.




- Re[17]: Смещение перигелия Меркурия и других планет
(В. В. Чазов,
15.03.2008 18:33, 798 Байт, ответов: 18)
Дорогие друзья, в ответе [14] уже заметил неточность. Речь идёт не о средних
квадратических погрешностях одного измерения, а об оценке ошибок a priori, то
есть до процесса фильтрации по методу наименьших квадратов. В процессе обработки, кроме
начальных условий, улучшены числовые значений более 20 параметров. По терминологии
уважаемого Сергея это означает следующее: в эфемеридах DE405 представлены данные
наблюдений, откорректированные расчетными данными, причём были использованы (для
Меркурия и Венеры) очень короткие по времени ряды радиолокационных измерений дальностей
средних точек поверхностей планет от радиотелескопа на Земле.
Уф, почти не запутался. Но на вопрос, где же здесь релятивизм, уже не смогу ответить.
С поклоном, Ваш Вадим. - Re[18]: Смещение перигелия Меркурия и других планет
(С. Ю. Юдин,
16.03.2008 9:53, 2.1 КБайт, ответов: 17)
Цитата: По терминологии уважаемого Сергея это означает следующее: в эфемеридах DE405 представлены данные наблюдений, откорректированные расчетными данными, причём были использованы (для Меркурия и Венеры) очень короткие по времени ряды радиолокационных измерений дальностей средних точек поверхностей планет от радиотелескопа на Земле.
Уф, почти не запутался. Но на вопрос, где же здесь релятивизм, уже не смогу ответить.
С поклоном, Ваш Вадим.Не, Вадим, давай с релятивизмом погодим, т.к. я никак не могу понять, что за данные апроксимированы полиномами Чебышева в эфемеридах DE405, по тому, что я не понимаю как это данные радиолокационных измерений могут быть расчетными данными, которые корректируют данные наблюдений. Ведь данные радиолокационных измерений это и есть данные наблюдений, по этому я не пойму как данные наблюдений могут откорректировать данные наблюдений. Эти данные радиолокационных измерений могут откорректировать только данные вычислительного эксперимента, полученные на модели Солнечной системы, т.е. по уравнению, которое мы никак не можем здесь показать. И таким образом получается, что в эфемеридах DE405 представлены данные, полученные при вычислительном эксперименте на модели Солнечной системы, причем не только данные после 2000 года, что само собой разумеется, но и с 1600 года по 2000 год. Не понятно только по каким данным создатели эфемерид DE405 корректировали данные вычислительного эксперимента с 1600 по 1970 годы, т.к. после 1970 года ясно, что они использовали данные радиолокационных измерений тех обсерваторий, о которых Вы написали. Или Вы хотите сказать, что расчетными данными откорректированы только данные радиолокационных измерений, а данные наблюдений прошлых веков не корректировались расчетными данными, т.е. данными полученными на математической модели.
С наилучшими пожеланиями Сергей Юдин.
- Re[19]: Смещение перигелия Меркурия и других планет (В. В. Чазов, 16.03.2008 15:02, 321 Байт, ответов: 16) Добрый день, Сергей, опять я невнятно написал, но Вы всё правильно расшифровали: ...расчетными данными откорректированы только данные радиолокационных измерений, а данные наблюдений прошлых веков не корректировались расчетными данными, т.е. данными полученными на математической модели.... С поклоном, Вадим.
- Re[20]: Смещение перигелия Меркурия и других планет
(С. Ю. Юдин,
16.03.2008 18:06, 1.9 КБайт, ответов: 15)
Цитата: опять я невнятно написал, но Вы всё правильно расшифровали: ...расчетными данными откорректированы только данные радиолокационных измерений, а данные наблюдений прошлых веков не корректировались расчетными данными, т.е. данными полученными на математической модели.... Ну, если я все правильно расшифровал, то теперь мне вообще ничего не понятно. Как это экспериментальные данные (причем такие точные) могут подгоняться под теорию (даже если она одобрена самим президентом). Обычно в науке теория подгоняется под экспериментальные данные. И потом, мне совершенно не понятно какова роль ОТОшной модели Солнечной системы JPL в создание эфемерид DE405. Если эти эфемериды до 2000 года являются аппроксимацией экспериментальных данных, то это можно было сделать и без модели Солнечной системы, аппроксимировав экспериментальные данные на интервалах от 8 до 32 дней обычной квадратичной зависимостью с применением метода наименьших квадратов (тогда и полиномы Чебышева не нужны). Но, если полиномами Чебышева аппроксимированы данные вычислительного эксперимента проведенного на модели Солнечной системы, то данные наблюдений при этом могут быть использованы только для контроля за правильностью работы модели и при этом никак нельзя говорить, что мы аппроксимировали именно данные наблюдений. А вот роль модели для создания эфемерид после 2000 года мне вполне понятна. И здесь в эфемеридах аппроксимированы конечно же данные вычислительного эксперимента проведенного на модели Солнечной системы, т.к. никаких наблюдательных данных из будущего у нас быть не может. Вот и возникает вопрос что же там в эфемеридах DE405 мы имеем.
С наилучшими пожеланиями Сергей Юдин.
- Re[21]: Смещение перигелия Меркурия и других планет
(В. В. Чазов,
16.03.2008 22:06, 1.4 КБайт, ответов: 14)
Дорогие друзья, добрый вечер.
Мне кажется, что наш уважаемый коллега Сергей опять сказал очень точно:
...если полиномами Чебышева аппроксимированы данные вычислительного эксперимента, проведённого на модели Солнечной системы, то данные наблюдений при этом могут быть использованы только для контроля за правильностью работы модели, и при этом никак нельзя говорить, что мы аппроксимировали именно данные наблюдений.
Эффекты общей теории относительности автоматически учитываются в процессе численного интегрирования дифференциальных уравнений движения объектов. Сами эти уравнения составлены в первом постньютоновском приближении (с точностью до квадрата отношения скорости гелиоцентрических движений планет к скорости света) с помощью "изотропных" координатных условий.
Эффект "замедления времени" в гравитационных полях учитывается во всех случаях:
независимой переменной эфемерид является специальное равномерное эфемеридное время,
в разницу моментов приёма и излучения радиоволн (измерение расстояний до планет) вводятся релятивистские поправки за гравитационные поля лоцируемой планеты, Земли и Солнца.
Замечательно, но тема, заданная Сергеем на форуме, может попасть в книгу рекордов Гиннеса по количеству текстов, на которые из больших специалистов так никто и не откликнулся.
To co-operation, keep well. Vadim. - Re[22]: Смещение перигелия Меркурия и других планет
(С. Ю. Юдин,
18.03.2008 11:02, 10.7 КБайт, ответов: 13)
Поиск экспериментальных данных наблюдений я конечно же продолжу, а сейчас я начал проводить предварительные эксперименты по определению оптимальных скоростей Солнечной системы (по осям координат) и скорости распространения гравитации, по критерию, когда данные по вековым смещениям параметров орбит, полученные на Ньютоновской математической модели Солнечной системы, где учтена скорость распространения гравитации, будут минимально отличаться от данных наблюдений. Параметры орбит решил пока вычислять только для Меркурия, т.к. эти эксперименты являются пока больше поисковыми. При этом, для определения оптимальных параметров системы я буду использовать многофакторное планирование. И сейчас уже выполнил первую серию экспериментов для четырехфакторного плана Бокса, где были следующие значения нулевых уровней и интервалов варьирования параметров VXsys=0+/-100, VYsys=0+/-100, VZsys=0+/- 100 и Vgr=11*Vsv+/-10*Vsv, где скорости системы в км/с, а скорость гравитации в долях скорости света Vsv. Вообще то при поисковых опытах не используют многофакторное планирование, а используют градиентные методы, но мне хотелось побыстрее проверить часть программы, отвечающую за многофакторное планирование, и по этому я сразу начал с него. А сейчас, чтобы было более понятно о чем будет идти речь, я коротко изложу основы многофакторного планирования.
Многофакторное планирование отличается от однофакторного, когда в каждом новом эксперименте изменяется значение только одного параметра (фактора), тем, что в каждом новом эксперименте изменяются по определенному плану все параметры. А после обработки экспериментальных данных мы получаем уравнение регрессии (чаще всего квадратичную аппроксимацию), которое отражает влияние всех параметров на критерий оптимизации (целевую функцию). Если у нас однофакторный эксперимент то мы получим такое уравнение
Y=k0+k1*X1+k2*X1^2 (1)
где Y критерий оптимизации, который надо минимизировать или максимизировать, X1 оптимизируемый параметр, а k0,k1 и k2 коэффициенты, которые мы получаем методом наименьших квадратов при статистической обработке данных. А вот, если у нас будет 4-е параметра, то мы получим уравнение регрессии следующего видаY = k0 + k1*X1 + k2*X2 + k3*X3 + k4*X4 +
+ k5*X1*X2 + k6*X1*X3 + k7*X1*X4 + k8*X2*X3 + k9*X2*X4 + k10*X3*X4 +
+ k11*X1^2 + k12*X2^2 + k13*X3^2 + k14*X4^2 (2)Принципиально это уравнение отличается от уравнения, полученного при однофакторном планирование, наличием смешанных коэффициентов k5 k10, которые отражают смешанное влияние параметров на критерий оптимизации. Задавая значения параметров в каждом эксперименте по определенному плану, мы получаем минимальное количество экспериментов необходимое для получения зависимости (2). Планы бывают разные и, например, в программе Plank я использовал четыре разных плана -ортогональный, ротатабельный, униформротатабельный и почти D- оптимальный Бокса. Отличаются они разным количеством уровней варьирования факторов, величиной звездного плеча и количеством нулевых точек, а в конечном итоге это влияет на то как будет размазана информация по гиперсфере. Мне, например, больше нравятся почти D- оптимальные планы Бокса и именно такой план мы и будем использовать.
Для получения уравнения (2) нам необходимо по плану Бокса выполнить 24 эксперимента. У этого плана факторы варьируются только на 3-х уровнях (включая нулевой) и звездное плечо будет равно 1. Обычно в планах 0 означает, что параметр берется на нулевом уровне, +1 на нулевом уровне плюс интервал варьирования и -1 - на нулевом уровне минус интервал варьирования, а т.к. у нас звездное плечо равно 1 и уровней всего три, можно писать просто 0 + - и по этому план Бокса для четырех факторов будет выглядеть следующим образом
1 + + + +
2 + + + -
3 + + - +
4 + + - -
5 + - + +
6 + - + -
7 + - - +
8 + - - -
Следующие 8 опытов повторяют первые 8. Только первый параметр принимает кругом значение -1.
17 + 0 0 0
18 0 0 0
19 0 + 0 0
20 0 0 0
21 0 0 + 0
22 0 0 0
23 0 0 0 +
24 0 0 0После обработки данных вычислительных экспериментов мы получим уравнение (2), которое (если у нас получилась поверхность, не имеющая седловых точек) дифференцируем по X1, X2, X3, X4 и получаем 4-е алгебраических уравнения. Решая теперь систему этих уравнений, находим оптимальные значения параметров X1, X2, X3, X4 при которых наша целевая функция (критерий оптимизации) принимает минимальное или максимальное значение. В нашем случае нам нужно минимальное значение, т.к. оптимизацию мы ведем по минимальной разности полученного при вычислительном эксперименте значения векового смещения параметра и значения параметра полученного при обработке данных натурных пассивных экспериментов (данных наблюдений). Конкретно у меня в программе критерий оптимизации вычисляется по формуле
Yu0(U) = SUMi,j ( kVesa(I, J) * Abs((YRas(I, J, U) - YNab(I, J)) / YNab(I, J)) / 100) (3)
Где: Yu0(U) разница между расчетным YRas(I, J, U) и наблюдаемым YNab(I, J) значением векового смещения в U-ом эксперименте (U=1...24) для I ой планеты и J-го параметра
kVesa(I, J) весовой коэффициент J-ого параметра для I ой планеты (от 1 до 100).Программа Solsys5 позволяет произвольно выбирать планеты и параметры, по которым надо производить оптимизацию, а весовые коэффициенты задаются вручную самим исследователем в файле SolsysPlan.dat, где задаются также и нулевые уровни параметров и их интервалы варьирования (задаются программно). Вообще то получение единых критериев оптимизации при решение многокритериальных задач вопрос даже более сложный, чем проблема вековых смещений параметров орбит, и я обычно терпеть не могу когда используют единые критерии оптимизации, полученные по принципу автомотовелофотопримусрадиоружье или с применением весовых коэффициентов. Правда подобными фокусами, где процветает махровый субъективизм, чаще всего пользуются исследователи социально-экономических или технико- экономических систем. И мне даже пришлось коренным образом модернизировать функционально- стоимостной анализ, чтобы можно было объективным путем получить единый критерий оптимизации для социально-экономических или технико-экономических систем. Но в нашем случае, т.к. влияние всех параметров на единый критерий оптимизации одной природы и носит количественный характер, я считаю вполне приемлемым использование весовых коэффициентов для получения единого критерия оптимизации, хотя ниже и привожу данные оптимизации по каждому параметру отдельно.
Сейчас я выполнил все 24 эксперимента плана, но как оказалось данные по некоторым экспериментам, когда скорость гравитации была на нижнем уровне, т.е. равна одной скорости света, получились не пригодными для получения за заданный промежуток времени (400 лет) данных по вековым смещениям параметров орбит. На приведенном ниже рисунке даны графики изменения параметров орбит для 2-го эксперимента плана, т.е. с параметрами +,+,+,-.
http://ser.t-k.ru/Ris/Plan1.gif (зеркало http://modsys.narod.ru/Ris/Plan1.gif)
Как видим, данные по перигелию и эксцентриситету хоть и не очень хорошего качества, но пригодны для обработки, а вот данные по углу восхождения и углу наклону можно использовать только для небольшого промежутка времени по тому, что угол наклона орбиты Меркурия за 150 лет уменьшился от 7 до 3 градусов, а потом начал опять увеличиваться. А угол восходящего узла за это время уменьшился с 48 градусов до нуля, а потом программа стала выдавать не минус 1 градус, а 359 градусов. Естественно при таких масштабных изменениях параметров орбит я не могу аппроксимировать их ни линейной, ни даже квадратичной зависимостью, чтобы найти вековые смещения. И в следующей версии программы я постараюсь что нибудь придумать, чтобы избавиться хотя бы от скачка в угле восхождения, например, буду его определять в радианах. А для того, чтобы выполнить качественные эксперименты на этой версии программы надо будет или уменьшить интервалы варьирования скоростей системы по осям или увеличить нулевой уровень скорости гравитации. Но, не смотря на не очень хорошее качество экспериментальных данных, для иллюстрации теоретического материала, я их все таки обработал и нашел коэффициенты для 2-х уравнений (2) по смещению перигелия Меркурия и по смещению его эксцентриситета, хотя, как следует из уравнения (3) можно было бы и сразу получить одно уравнение по единому критерию оптимизации. И ниже Вы видите как по уравнениям (2) каждый из параметров влияет на критерий оптимизации, когда остальные параметры зафиксированы на нулевых уровнях.
http://ser.t- k.ru/Ris/Box1.gif (зеркало http://modsys.narod.ru/Ris/Box1.gif)В принципе ничего интересного на этих графиках нет, и мы видим то, о чем я уже сказал выше. Т.е. при тех скоростях распространения гравитации, которые я использовал в вычислительных экспериментах, все оптимальные скорости системы по осям ... Z жмутся к нулевому уровню, а оптимальное значение скорости распространения гравитации находится явно за пределами варьирования (в сторону увеличения). Хотя, при большом желании, и по уже полученным уравнениям (2) можно чисто математически найти оптимальные скорости системы и оптимальную скорость распространения гравитации. Вот только в нашем случае этого делать никак нельзя (даже если очень хочется), т.к. оптимальное значение скорости распространения гравитации находится явно за пределами варьирования параметров. А я лично, к тому же, стараюсь еще получить всегда оптимум не просто в пределах интервала варьирования параметров, но и при минимальных интервалах варьирования параметров и чтобы оптимум получился вблизи нулевого уровня и по каждому параметру отдельно (не очень то я все таки доверяю логике математической целесообразности и комбинированным критериям оптимизации). Но при правильном подборе весовых коэффициентов комбинированный критерий оптимизации может оказаться очень даже полезен.
В дополнение к сделанным выводам могу также сказать, что, как известно из литературных источников, абсолютная скорость Солнечной системы, по данным реликтового излучения, составляет VXsys= -358, VYsys= 57, VZsys= -73 км/с, т.е. интервалы варьирования скорости системы я задал в плане вполне приемлемые и, следовательно, если моя модель правильно отражает объективную реальность, причина столь сильных изменений параметров орбит заключается в очень маленькой скорости гравитации. По этому я сейчас выполню новый план, где скорость гравитации задам Vgr=50*Vsv+/-30*Vsv.
С наилучшими пожеланиями Сергей Юдин.
- Re[23]: Смещение перигелия Меркурия и других планет
(С. Ю. Юдин,
20.03.2008 21:50, 561 Байт, ответов: 12)
Попробовал на сайте Института небесной механики и вычисления эфемерид Франции найти эфемериды отличающиеся от эфемерид JPL и даже на их FTP сервере ftp://ftp.imcce.fr/ в папке ftp://ftp.imcce.fr/pub/ephem/sun вроде бы нашел какие то эфемериды, но что это за эфемериды и как ими пользоваться я с моим знанием английского языка и астрономии не понял. Буду благодарен, если кто ни будь поможет мне в этом разобраться.
С наилучшими пожеланиями Сергей Юдин.
- Re[24]: Смещение перигелия Меркурия и других планет
(В. В. Чазов,
21.03.2008 6:27, 1.4 КБайт, ответов: 11)
Дорогие друзья.
Над созданием эфемерид Института небесной механики и вычисления эфемерид Франции группа энтузиастов начала работу после войны 1974 года на Ближнем Востоке. Исторически претензии этих отважных мушкетёров вполне обоснованы: необходимо было заменить модели движения небесных тел, разработанные мэтром Урбаном Жозефом де Ле-Веррье.
Поступили так: получили финансирование от Интенданта финансов (а как же не дать, Франция всегда впереди!), съездили в Калифорнию, скопировали на магнитную ленту числовые данные эфемериды DE102/LE51 Лаборатории реактивного движения США (Пасадена, КалТех), посетили Голивуд, вежливо (по-французски) поблагодарили и вернулись в Париж. Года за четыре на компьютере CDC с 32 значащими цифрами (это у них называется двойной точностью) апппроксимировали данные с магнитной ленты JPL рядами Фурье и опубликовали статью, в которой около 10000 коэффициентов этих рядов назвали новой моделью движения планет.
Дальше - больше. С появлением каждой новой версией эфемерид JPL на службу в Институт небесной механики Парижа поступал новый сотрудник для получения новых коэффициентов рядов Фурье.
И это - правильно. Именно таким способом удаётся получать финансирование, ибо в Парламенте уверены, что учёные Парижа следуют традициям своих великих предшественников.
С поклоном, Ваш Вадим. - Re[25]: Смещение перигелия Меркурия и других планет
(С. Ю. Юдин,
21.03.2008 8:13, 7.8 КБайт, ответов: 10)
План выполнил, данные обработал, а сейчас крепко задумался. К сожалению никакого глобального оптимума достичь не получилось, хотя данные для подобных планов многофакторного планирования получились просто отличные, если не считать двух последних экспериментов. Да Вы взгляните сами на результаты вычислительных экспериментов для Меркурия по плану Бокса, где факторы варьировались в следующих интервалах VXsys= 0+/-100, VYsys= 0+/-100, VZsys= 0+/-100, Vgr= 50*Vsv+/-30*Vsv (скорости системы по осям в км/с, а скорость гравитации в долях скорости света). Обозначения для вековых смещений параметров орбит те же, что были и раньше dAlfaP перигелий, dAlfaU узел восхождения, dBetta наклон орбиты и dEks эксцентриситет. Полученные смещения углов у меня даны в угловых секндах, а безразмерные значения вековых смещений эксцентриситетов увеличены мною в 3600 раз. В нулевой строке даны вековые смещения параметров орбит определенные по данным DE405 при неизвестных нам значениях факторов, которые и надо найти как оптимальные.
________dAlfaP__dAlfaU__dBetta__dEks
0__????___572,2__-450,0__- 21,4__0,074
1__++++__451,3__-1402__-230,5__0,208
2__+++-__234,8__-449,1__- 838,2__0,800
3__++-+__472,7__428,9___183,6__0,257
4__++--__ 273,5___2765___794,0__0,654
5__+-++__566,7__-1560__-263,2__0,302
6__+-+-__730,5___- 5206__-956,1__0,833
7__+--+__587,9___283,7__149,1___0,350
8__+--- ___791,0__2254___647,1___0,977
9__-+++__470,2__-1228__-194,1__-0,205
10_-++- ___289,0__-3858__-723,6__-1,071
11_-+-+___491,5__609,9___225,8__-0,154
12_-+-- ___376,5___3518___1002__-0,850
13_--++__586,1__-1386___-227,5__-0,110
14_--+- ___760,1__-4581__-848,4__-0,667
15_--+-___607,3__464,0___190,6__-0,061
16_---- ____845,2__3002___845,7__-0,468
17_+000__513,2__-591,8__-52,3____0,401
18_- 000__544,7__-307,6___10,0___-0,258
19_0+00__436,8__-329,4___5,8____-0,001
20_0- 00__621,4__-572,2___-48,6___0,148
21_00+0__512,3__-1984__-352,8___0,036
22_00- 0__545,9___963,4__312,8___0,114
23_000+__529,0__-450,9__-21,5___0,074
24_000- __529,1__-450,5___-21,5___0,074Графики влияния каждого из факторов на критерий оптимизации по уравнению (2), когда остальные факторы зафиксированы на нулевых уровнях, я не привожу, т.к. по всем факторам они будут примерно такие же как и в первом плане для которого я их приводил. И определенный вывод по ним можно сделать только один глобальный оптимум по скорости гравитации находится где то за верхним уровнем, т.е. больше 80*Vsv. И я уже даже предчувствую критику знатоков планирования экспериментов за то, что я сразу стал ставить полные планы второго порядка, вместо того чтобы совершить крутое восхождение в область оптимума и уже там ставить полный план второго порядка, т.е. так как надо по классическим правилам планирования экспериментов. На что я могу ответить, что, во-первых, как я уже писал, мне хотелось побыстрее опробовать код программы по многофакторному планированию, а не излагать классическую теорию многофакторного планирования, во-вторых, некоторые поисковые эксперименты я все же проводил, и в третьих, самое главное, проводя вычислительные эксперименты на моделях систем, я всегда, вопреки рекомендациям классиков, использую только планы второго порядка.
Объясняется это тем, что, во-первых, число экспериментов, если мы не используем дробные реплики со смешанными коэффициентами (а дробные реплики отрицательно влияют на качество получаемой информации) при построение матрицы линейного плана для осуществления крутого восхождения, получается не на много меньше, чем при планах второго порядка (16 вместо 24), что при проведение вычислительных экспериментов не на много увеличит время их проведения (материальных затрат при этом практически никаких), а, во- вторых, чтобы методом крутого восхождения достичь области близкой к оптимуму надо выполнить 510 планов первого порядка и при этом общее число экспериментов может быть даже больше, т.к. информации от уравнения регрессии второго порядка можно получить гораздо больше и, следовательно, за меньшее число шагов достичь области оптимума. А кроме этого, если мы используем планы второго порядка, как при поисковых экспериментах, так и при изучении поверхности отклика в области оптимума, обработка данных производится по одной методике, что значительно упрощает код программы. Вот если бы эксперименты у нас были не вычислительные, т.е. не на математической модели, а натурные и нам в каждом эксперименте приходилось бы, например, запускать натуральную ракету к одной из планет, то тут можно было бы и подумать о различных градиентных методах для поиска области оптимума, т.к. после этих 48 экспериментов все исследования, наверное, и закончились бы, т.к. просто кончились бы деньги, выделенные на эти исследования. В нашем же случае, т.к. персональный компьютер потребляет не много электроэнергии, приходится жалеть только о затраченном времени.
А вообще-то, честно говоря, после этой серии экспериментов, я нахожусь в некотором замешательстве (неопределенности). Нечто подобное у меня было, когда я оптимизировал коэффициенты в формуле Планка, когда мне вследствие неопределенности решений никак не удавалось найти оптимум, но тогда я все таки нашел решение этого вопроса (кому интересно могу посмотреть это здесь http://ser.t-k.ru/Stat/Plank/plank.html зеркало http://modsys.narod.ru/Stat/Plank/plank.h tml ). А вот в этом случае я имею не только некоторую неопределенность, т.к., например, как видно из полученных данных, оптимум по всем вековым смещениям, кроме перигелия, может быть найден даже в уже заданных интервалах варьирования (кроме скорости гравитации). Вот только может получиться так, что каждый раз, выходя из разных точек гиперпространства, я буду каждый раз находить разные значения факторов для глобального оптимума. Но особенно меня смущает то, что пока выходит, что оптимальная скорость распространения гравитации лежит даже за пределами восьмидесяти скоростей света. Да, из литературных источников я знаю, что у многих исследователей теоретические значения скорости распространения гравитации получались очень большие, но одно дело об этом просто читать, а другое дело столкнутся с этим практически. Так что здесь у меня вдобавок к неопределенности существует еще и психологический барьер. Ведь мы уже все привыкли к тому, что скорость распространения для любых явлений Природы не может превышать скорость света.
Так что это действительно редкий случай, когда я принципиально не знаю что делать. А пока я буду осмысливать сложившуюся ситуацию, я решил выполнить еще один план, чтобы компьютер не простаивал, где решил задать на нулевом уровне скорость распространения гравитации 150 скоростей света. На всякий случай, решил немного изменить нулевые уровни и скоростей системы, а то не очень хорошо получается, когда на нулевых уровнях они все равны нулю. В общем, решил выполнить план с факторами VXsys= -50+/-100, VYsys= 0+/-100, VZsys= -50+/-100, Vgr= 150*Vsv+/-50*Vsv. Правда, в конечном итоге может оказаться, что все мои проблемы связаны с тем, что модель Солнечной системы, построенная на законах Ньютона (за исключением третьего закона), даже с учетом скорости распространения гравитации, просто не адекватно описывает процессы, происходящие в Природе, или, как говорят классики многофакторного планирования, у нас имеется не учтенный фактор, но пока у меня нет достаточных оснований, чтобы так заявить. А не учтенным фактором может быть и искривление пространства-времени, которое учитывается в ОТО, и динамическое давление гравитационного поля, которое учитывал Гербер, или еще что ни будь. Так что, как говорил Ю.Никулин //Будем искать//.
С наилучшими пожеланиями Сергей Юдин.
- Re[26]: Смещение перигелия Меркурия и других планет
(С. Ю. Юдин,
31.03.2008 15:46, 19.7 КБайт)
Обработал данные третьего плана многофакторного планирования и получил опять результаты, которые позволяют сделать только один вывод скорость распространения гравитации должна быть больше чем 200 скоростей света. Это меня заставило задуматься о том все ли у меня в порядке с теоретическим обоснованием этого моего исследования, т.к., проводя ранее подобные исследования, я обычно за два шага уверенно приходил в область оптимума, а здесь сделал три шага и оптимума не видно. И я стал даже задумываться о том, что может быть методы многофакторного планирования по тому критерию оптимизации, что я использую, не очень подходят для этого. Ведь до этого исследования, если не считать случая по оптимизации коэффициентов в формуле Планка, я оптимизировал параметры систем по отклику системы, а не по разнице между откликом и заданным оптимальным значением (в нашем случае в формуле (3), которую я приводил выше, между расчетными, т.е. полученными при вычислительном эксперименте на модели, YRas(I, J, U) и наблюдаемыми YNab(I, J) значениями вековых смещений в U-ом эксперименте для I ой планеты и J-го параметра). В дальнейшем этот критерий я буду называть dY в противовес критерию Y, который обычно применяется при многофакторном планировании, и где, при проведение натурных экспериментов, Yu0(U)= YNab(U), а, при проведение вычислительных экспериментов, Yu0(U)= YRas(U).
Yu0(U) = SUMi,j ( kVesa(I, J) * Abs ((YRas(I, J, U) - YNab(I, J)) / YNab(I, J)) / 100) (3)
Вообще то в книге С.В.Мельников, В.Р.Алешкин, П.М.Рощин Планирование эксперимента в исследованиях сельскохозяйственных процессов Л. Колос 1980 на стр. 45 для расчета комплексного критерия приводится формула подобная моей формуле (3). Там только используется не абсолютное значение относительной разности между откликом системы и оптимальным значением, а квадрат этой разности, т.е. критерий dY^2, но, как пишут авторы, это делается только для того, чтобы разность была всегда положительной. Я же в своей формуле использовал абсолютное значение этой разницы, т.е. принципиальных отличий от их формулы у меня нет и, следовательно, я могу смело использовать свой критерий оптимизации dY для оптимизации параметров Солнечной системы. Но одно дело, что у них там написано, а другое дело то, что я вижу. Да и мой собственный опыт с коэффициентами в формуле Планка (1t) не очень показательный, т.к. оптимизировал я там только 3 коэффициента, а 4-ый фактор (температура излучения) мною принудительно задавался для повышения качества информации при проведение вычислительных экспериментов по почти D-оптимальному плану Бокса для четырех факторов. К тому же второй коэффициент (показатель степени при частоте излучения v) мне надо было не столько оптимизировать, сколько подтвердить, что он равен 3, как это следовало из формулы Вина. Таким образом, я по большому счету оптимизировал только 2 параметра (фактора) и, следовательно, у меня могли быть только двойные смешанные взаимодействия, а это прекрасно воспроизводится полиномом 2-ой степени (2), который я получаю после обработки данных вычислительных экспериментов.
А кто может ответить на вопрос есть ли в нашей системе, которую мы исследуем, смешанные взаимодействия выше парных, т.е. тройные или четверные. А может быть даже есть и не только линейные взаимодействия, но и квадратичные. К сожалению, ответить на эти вопросы никто не может. Да, наверное, никто не сможет ответить и на то, как это скажется на описание поверхности отклика при таких условиях. По этому, я на всякий случай (не очень доверяя всему, что написано в учебниках) решил провести маленькое исследование по оптимизации по критериям dY и dY^2 параметров простейших математических выражений, которые будут имитировать поведение различных систем. И первым делом я решил взять чуть ли не самый сложный случай с четверным взаимодействием, где вдобавок одно взаимодействие еще и не линейно, т.е. всем Вам известный закон тяготения Ньютона (3t) и попробовать оптимизировать его параметры. В принципе, мы можем с законом тяготения провести и натурные эксперименты. Правда, не с самим законом тяготения для масс, а с законом тяготения для зарядов (закон Кулона), где даже аналог гравитационной постоянной можем изменять, распологая различные диэлектрики между зарядами. Но речь сейчас идет не о том, можем ли мы воспроизвести эксперименты на реальном объекте или на его модели, а о том, можем ли мы, уже даже зная аналитическую формулу, отражающую отклик системы на наши воздействия на нее, чисто с математической точки зрения получить оптимальные значения системы по примененному мною критерию dY, т.е. по разнице между откликом системы и известным оптимальным значением.
Может возникнуть вопрос а зачем вообще надо проводить исследования для получения аппроксимации (2), если у нас уже есть аналитическая формула закона тяготения. А затем, что, мы сейчас просто проверяем на что способны методы многофакторного планирования, чтобы заранее знать, что от них ожидать. Ведь когда мы исследуем какую то сложную систему, то нам надо проводить натурные или вычислительные эксперименты, чтобы получить хотя бы уравнение регрессии (2), т.к. никакие аналитические выражения для критерия оптимизации при исследование самого объекта нам не известны вообще, а аналитическая формула, по которой вычисляется критерий оптимизации в моделях объекта, даже если и удастся такую получить в развернутом виде, может уместиться только на десятках или сотнях страниц, что делает ее не пригодной для аналитических методов оптимизации. А уравнение регрессии (2), т.е. полином 2-го порядка, который мы получаем при многофакторном планировании, очень удобен для этого и по этому мы и постараемся его получить по критерию dY для тестируемых систем. А т.к. в программе Solsys5 у меня по формуле (3) рассчитывается значение комплексного критерия оптимизации (целевой функции) в каждом из 24 экспериментов, а отклик системы в наших тестовых примерах определяется не по комплексному критерию, то мы можем, для оптимизации параметров по критерию dY в тестовых выражениях (3t10t), формулу (3) упростить до выражения (4)
Yu0(U) = Abs((YRas(U) - Yopt) / Yopt) (4)
Где: Yu0 (U) относительная разница между расчетным YRas(U) и оптимальным Yopt значением отклика системы, поведение которой имитирует одна из формул (3t10t), в U-ом эксперименте.Результаты оптимизации параметров в формуле тяготения, по примененному мною критерию оптимизации dY, получились удручающие, т.к. аппроксимация критерия оптимизации, полученным уравнением регрессии (2), не лезла ни в какие ворота. Да Вы сами взгляните на полученные значения критерия оптимизации dY с использованием формулы закона тяготения (3t) и эти же значения по полученному уравнению регрессии (2) на нижеприведенном рисунке (верхняя часть рисунка), где маленькие синие кружки это критерий оптимизации рассчитанный с использованием формулы (3t) для выражения (3) в 24 экспериментах плана Бокса (номер соответствует абсциссе), а большие синие кружки это критерий оптимизации, рассчитанный по уравнению регрессии (2), для тех же значений параметров, что и в соответствующем эксперименте. При этом все факторы X1 X4, при выполнение плана Бокса, на нулевом уровне были равны единице, а интервалы их варьирования были 0,5, а значение Yopt бралось равным 1, т.е. я принимал, что оптимальные значения параметров X1 X4 в формуле (3t) равны 1 и получалось, что Yopt = 1*1*1/1=1. Для меня такой результат аппроксимации был большой неожиданностью, т.к. ранее в своей книге я сам закон тяготения, т.е. по критерию Y, аппроксимировал уравнением (2) и никаких проблем по качеству аппроксимации тогда не было. Я тут же аппроксимировал полученные значения Yu0(U) полиномом (2) и по критерию Y и выяснилось, что на этот раз у меня получились значительные погрешности в аппроксимации (синие маленькие и большие кружки на нижней части рисунка).
Yu = k0 + k1*X1 + k2*X2 + k3*X3 + k4*X4 +
+ k5*X1*X2 + k6*X1*X3 + k7*X1*X4 + k8*X2*X3 + k9*X2*X4 + k10*X3*X4 +
+ k11*X1^2 + k12*X2^2 + k13*X3^2 + k14*X4^2 (2)
где Yu (или dYu или dYu^2) критерий оптимизации, который надо минимизировать, X1 X4 - оптимизируемые параметры, а k0 k14 коэффициенты, которые мы получаем методом наименьших квадратов при статистической обработке значений Yu0(U) полученных в 24 экспериментах при разных значениях параметров X1 X4.http://ser.t-k.ru/Ris/3t_Y_dY.gif (зеркало http://modsys.narod.ru/Ris/3t_Y_dY.gif)
Стал разбираться в чем дело и выяснил, что когда я ранее аппроксимировал закон притяжения, то задавал интервалы варьирования параметров примерно 20%, а сейчас задал их 50%. Уменьшил интервал варьирования до 20% и на сей раз опять получил приличный результат (черные кружки), т.е. получается, что все дело не в самом критерии оптимизации, а в интервалах варьирования, тем более, что при интервалах варьирования 80% (зеленые кружки), результат получился еще хуже, чем при 50%. И по критерию dY (в верхней части рисунка) тоже получается, что, чем больше интервал варьирования, тем хуже аппроксимация экспериментальных данных, но здесь уже не все так однозначно, т.к. получается, что и при интервале варьирования 20% аппроксимация экспериментальных данных получается не на много лучше. По этому я решил продолжить исследование с использованием других математических выражений имитирующих поведение системы.
YRas(U) = X1*v^X2* exp(-X3*v/X4) (1t)
YRas(U) = u (2t)
YRas(U) = X1 * X2 * X3 / X4^2 (3t)
YRas(U) = X1^2 * X2^2 (4t)
YRas(U) = X1 * X2 * X3 * X4 (5t)
YRas(U) = X1 + X1^2 (6t)
YRas(U) = X1 + X2 + X3 + X4 (7t)
YRas(U) = X1*X2 + X1*X3 + X1